Merging Alternate Remotely-Sensed Soil Moisture Retrievals Using a Non-Static Model Combination Approach
Abstract
:1. Introduction
2. Data and Processing
2.1. Data
2.1.1. Remotely-Sensed Soil Moisture Products
2.1.2. Reanalysis Soil Moisture Products
2.1.3. In Situ Soil Moisture Measurements and Ancillary Data
2.2. Data Preprocessing
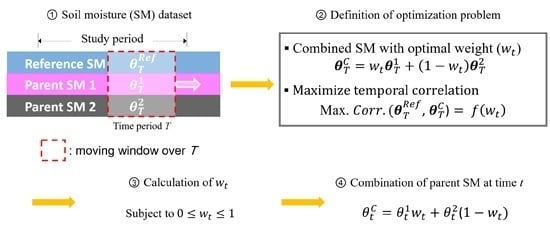
3. Methodology
3.1. Static Linear Combination
3.2. Dynamic Linear Combination
4. Results
4.1. Global Data Combination with Various Scenarios
4.2. A Simulation Experiment
4.3. Comparison against in Situ Observations
4.4. Influence of the Quality of the Parent Products and Reference
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.; Kanae, S.; Kowalczyk, E.; Lawrence, D. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed]
- Taylor, C.M.; de Jeu, R.A.M.; Guichard, F.; Harris, P.P.; Dorigo, W.A. Afternoon rain more likely over drier soils. Nature 2012, 489, 423–426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paloscia, S.; Macelloni, G.; Santi, E. Soil Moisture Estimates from AMSR-E Brightness Temperatures by Using a Dual-Frequency Algorithm. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3135–3144. [Google Scholar] [CrossRef]
- Akbar, R.; Moghaddam, M. A Combined active–passive soil moisture estimation algorithm with adaptive regularization in support of SMAP. IEEE Trans. Geosci. Remote Sens. 2014, 53, 3312–3324. [Google Scholar] [CrossRef]
- Wagner, W.; Hahn, S.; Kidd, R.; Melzer, T.; Bartalis, Z.; Hasenauer, S.; Figa-Saldaña, J.; de Rosnay, P.; Jann, A.; Schneider, S. The ASCAT soil moisture product: A review of its specifications, validation results, and emerging applications. Meteorol. Z. 2013, 22, 5–33. [Google Scholar] [CrossRef]
- Fujii, H.; Koike, T.; Imaoka, K. Improvement of the AMSR-E algorithm for soil moisture estimation by introducing a fractional vegetation coverage dataset derived from MODIS data. J. Remote Sens. Soc. Jpn. 2009, 29, 282–292. [Google Scholar]
- Owe, M.; De Jeu, R.A.M.; Holmes, T. Multisensor historical climatology of satellite-derived global land surface moisture. J. Geophys. Res. Earth Surf. 2008. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Wagner, W.; Bloschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Nord. Hydrol. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 2014JD021489. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Meesters, A.G.C.A.; Liu, Y.; Dorigo, W.; Wagner, W.; De Jeu, R.A.M. Error estimates for near-real-time satellite soil moisture as derived from the land parameter retrieval model. IEEE Geosci. Remote Sens. Lett. 2011, 8, 779–783. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Liu, P.; Mahanama, S.P.P.; Njoku, E.G.; Owe, M. Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) and the Scanning Multichannel Microwave Radiometer (SMMR). J. Geophys. Res. Atmos. 2007. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Hasenauer, S. ASCAT soil wetness index validation through in situ and modeled soil moisture data in central Italy. Remote Sens. Environ. 2010, 114, 2745–2755. [Google Scholar] [CrossRef]
- Gruhier, C.; de Rosnay, P.; Hasenauer, S.; Holmes, T.; de Jeu, R.; Kerr, Y.; Mougin, E.; Njoku, E.; Timouk, F.; Wagner, W.; et al. Soil moisture active and passive microwave products: Intercomparison and evaluation over a Sahelian site. Hydrol. Earth Syst. Sci. 2010, 14, 141–156. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Gruber, A.; De Jeu, R.A.M.; Wagner, W.; Stacke, T.; Loew, A.; Albergel, C.; Brocca, L.; Chung, D.; Parinussa, R.M.; et al. Evaluation of the ESA CCI soil moisture product using ground-based observations. Remote Sens. Environ. 2015, 162, 380–395. [Google Scholar] [CrossRef]
- Su, C.-H.; Ryu, D.; Young, R.I.; Western, A.W.; Wagner, W. Inter-comparison of microwave satellite soil moisture retrievals over the Murrumbidgee Basin, southeast Australia. Remote Sens. Environ. 2013, 134, 1–11. [Google Scholar] [CrossRef]
- Rüdiger, C.; Calvet, J.-C.; Gruhier, C.; Holmes, T.R.; de Jeu, R.A.; Wagner, W. An intercomparison of ERS-Scat and AMSR-E soil moisture observations with model simulations over France. J. Hydrometeorol. 2009, 10, 431–447. [Google Scholar] [CrossRef]
- Crow, W.T.; Miralles, D.G.; Cosh, M.H. A Quasi-Global Evaluation System for Satellite-Based Surface Soil Moisture Retrievals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2516–2527. [Google Scholar] [CrossRef]
- Yilmaz, M.T.; Crow, W.T. Evaluation of Assumptions in Soil Moisture Triple Collocation Analysis. J. Hydrometeorol. 2014, 15, 1293–1302. [Google Scholar] [CrossRef]
- Gruber, A.; Su, C.H.; Zwieback, S.; Crow, W.; Dorigo, W.; Wagner, W. Recent advances in (soil moisture) triple collocation analysis. Int. J. Appl. Earth Obs. Geoinform. 2016, 45, 200–211. [Google Scholar] [CrossRef]
- Kim, S.; Liu, Y.Y.; Johnson, F.M.; Parinussa, R.M.; Sharma, A. A global comparison of alternate AMSR2 soil moisture products: Why do they differ? Remote Sens. Environ. 2015, 161, 43–62. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; Dong, J.; Berg, A.A. Global Soil Moisture from Satellite Observations, Land Surface Models, and Ground Data: Implications for Data Assimilation. J. Hydrometeorol. 2004, 5, 430–442. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Parinussa, R.M.; Dorigo, W.A.; De Jeu, R.A.M.; Wagner, W.; van Dijk, A.I.J.M.; McCabe, M.F.; Evans, J.P. Developing an improved soil moisture dataset by blending passive and active microwave satellite-based retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 425–436. [Google Scholar] [CrossRef] [Green Version]
- Yilmaz, M.T.; Crow, W.T. The optimality of potential rescaling approaches in land data assimilation. J. Hydrometeorol. 2013, 14, 650–660. [Google Scholar] [CrossRef]
- Entekhabi, D.; Reichle, R.H.; Koster, R.D.; Crow, W.T. Performance metrics for soil moisture retrievals and application requirements. J. Hydrometeorol. 2010, 11, 832–840. [Google Scholar] [CrossRef]
- Kim, S.; Parinussa, R.M.; Liu, Y.Y.; Johnson, F.M.; Sharma, A. A framework for combining multiple soil moisture retrievals based on maximizing temporal correlation. Geophys. Res. Lett. 2015, 42, 6662–6670. [Google Scholar] [CrossRef]
- Parinussa, R.M.; Holmes, T.R.H.; Wanders, N.; Dorigo, W.A.; de Jeu, R.A.M. A Preliminary Study toward Consistent Soil Moisture from AMSR2. J. Hydrometeorol. 2014, 16, 932–947. [Google Scholar] [CrossRef]
- Mo, T.; Choudhury, B.J.; Schmugge, T.J.; Wang, J.R.; Jackson, T.J. A model for microwave emission from vegetation-covered fields. J. Geophys. Res. Oceans 1982, 87, 11229–11237. [Google Scholar] [CrossRef]
- Terui, N.; van Dijk, H.K. Combined forecasts from linear and nonlinear time series models. Int. J. Forecast. 2002, 18, 421–438. [Google Scholar] [CrossRef]
- Chowdhury, S.; Sharma, A. Multisite seasonal forecast of arid river flows using a dynamic model combination approach. Water Resour. Res. 2009. [Google Scholar] [CrossRef]
- Khan, M.Z.K.; Mehrotra, R.; Sharma, A.; Sankarasubramanian, A. Global Sea Surface Temperature Forecasts Using an Improved Multimodel Approach. J. Clim. 2014, 27, 3505–3515. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Kasahara, M.; Ito, N.; Nakagawa, K.; Oki, T. Instrument performance and calibration of AMSR-E and AMSR2. In International Archives of the Photogrammetry, Remote Sensing and Special Information Science; International Society of Photogrammetry and Remote Sensing: Kyoto, Japan, 2010. [Google Scholar]
- De Jeu, R.A.M.; Wagner, W.; Holmes, T.R.H.; Dolman, A.J.; Giesen, N.C.; Friesen, J. Global Soil Moisture Patterns Observed by Space Borne Microwave Radiometers and Scatterometers. Surv. Geophys. 2008, 29, 399–420. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Reichle, R.H.; Koster, R.D.; De Lannoy, G.J.M.; Forman, B.A.; Liu, Q.; Mahanama, S.P.P.; Touré, A. Assessment and Enhancement of MERRA Land Surface Hydrology Estimates. J. Clim. 2011, 24, 6322–6338. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Wagner, W.; Hohensinn, R.; Hahn, S.; Paulik, C.; Xaver, A.; Gruber, A.; Drusch, M.; Mecklenburg, S.; van Oevelen, P.; et al. The International Soil Moisture Network: A data hosting facility for global in situ soil moisture measurements. Hydrol. Earth Syst. Sci. 2011, 15, 1675–1698. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dorigo, W.A.; Parinussa, R.M.; de Jeu, R.A.M.; Wagner, W.; McCabe, M.F.; Evans, J.P.; van Dijk, A.I.J.M. Trend-preserving blending of passive and active microwave soil moisture retrievals. Remote Sens. Environ. 2012, 123, 280–297. [Google Scholar] [CrossRef]
- Wagner, W.; Dorigo, W.; de Jeu, R.; Fernandez, D.; Benveniste, J.; Haas, E.; Ertl, M. Fusion of active and passive microwave observations to create an essential climate variable data record on soil moisture. In Proceedings of the XXII ISPRS Congress, Melbourne, Australia, 25 August–1 September 2012; pp. 315–321.
- Koike, T. Soil moisture algorithm. In Descriptions of GCOM-W1 AMSR2 (Rev. A); Earth Observation Research Center, Japan Aerospace Exploration Agency: Tokyo, Japan, 2013; pp. 8–13. [Google Scholar]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling sparse ground-based soil moisture observations for the validation of coarse-resolution satellite soil moisture products. Rev. Geophys. 2012. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.; Zwieback, S.; Xaver, A.; Wagner, W. Characterizing coarse-scale representativeness of in situ soil moisture measurements from the International Soil Moisture Network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Xaver, A.; Vreugdenhil, M.; Gruber, A.; Hegyiová, A.; Sanchis-Dufau, A.D.; Zamojski, D.; Cordes, C.; Wagner, W.; Drusch, M. Global automated quality control of in situ soil moisture data from the International Soil Moisture Network. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Dorigo, W.A.; Department of Geodesy and Geo-Information, Vienna University of Technology. Personal Communication, 2014.
- De Lannoy, G.J.M.; Reichle, R.H. Global Assimilation of Multi-Angle and Multi-Polarization SMOS Brightness Temperature Observations into the GEOS-5 Catchment Land Surface Model for Soil Moisture Estimation. J. Hydrometeorol. 2015. [Google Scholar] [CrossRef]
- Draper, C.S.; Walker, J.P.; Steinle, P.J.; De Jeu, R.A.M.; Holmes, T.R.H. An evaluation of AMSR–E derived soil moisture over Australia. Remote Sens. Environ. 2009, 113, 703–710. [Google Scholar] [CrossRef]
- Bates, J.M.; Granger, C.W. The combination of forecasts. Oper. Res. Q. 1969, 20, 451–468. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Ramanathan, R. Improved methods of combining forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- Clemen, R.T. Combining forecasts: A review and annotated bibliography. Int. J. Forecast. 1989, 5, 559–583. [Google Scholar] [CrossRef]
- Timmermann, A. Forecast Combinations. In Handbook of Economic Forecasting; Elliott, G., Timmermann, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 1, pp. 135–196. [Google Scholar]
- Sharma, A.; Mehrotra, R. An information theoretic alternative to model a natural system using observational information alone. Water Resour. Res. 2014, 50, 650–660. [Google Scholar] [CrossRef]
- Albergel, C.; de Rosnay, P.; Balsamo, G.; Isaksen, L.; Muñoz-Sabater, J. Soil Moisture Analyses at ECMWF: Evaluation Using Global Ground-Based In Situ Observations. J. Hydrometeorol. 2012, 13, 1442–1460. [Google Scholar] [CrossRef]
- Balsamo, G.; Albergel, C.; Beljaars, A.; Boussetta, S.; Brun, E.; Cloke, H.; Dee, D.; Dutra, E.; Muñoz-Sabater, J.; Pappenberger, F.; et al. ERA-Interim/Land: A global land surface reanalysis data set. Hydrol. Earth Syst. Sci. 2015, 19, 389–407. [Google Scholar] [CrossRef]









| Data Source | Dataset | Temporal Resolution | Spatial Resolution | Units |
|---|---|---|---|---|
| AMSR2-JAXA | Level 3 geophysical parameter SMC | Daily | 0.25° | m3/m3 |
| AMSR2-LPRM | Level 3 Surface Soil Moisture X-band | Daily | 0.25° | m3/m3 |
| AMSR2-LPRM | Vegetation optical depth C-band | Daily | 0.25° | - |
| AMSR2 | Scan time | Daily | 0.25° | s |
| ERA-Interim | Soil water contents Level 1 0–0.07-m depth | 6 h | 0.25° | m3/m3 |
| ERA-Interim | Soil temperature Level 1 0–0.07-m depth | 6 h | 0.25° | K |
| MERRA-Land | Top soil layer soil moisture consent SFMC | Hourly | 0.25° Resampled | m3/m3 |
| ISMN | In situ measured soil moisture from 124 stations in 10 networks | Hourly | Point | m3/m3 |
| ESA CCI | Topographic complexity, wetland fraction | - | 0.25° | % |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Parinussa, R.M.; Liu, Y.Y.; Johnson, F.M.; Sharma, A. Merging Alternate Remotely-Sensed Soil Moisture Retrievals Using a Non-Static Model Combination Approach. Remote Sens. 2016, 8, 518. https://doi.org/10.3390/rs8060518
Kim S, Parinussa RM, Liu YY, Johnson FM, Sharma A. Merging Alternate Remotely-Sensed Soil Moisture Retrievals Using a Non-Static Model Combination Approach. Remote Sensing. 2016; 8(6):518. https://doi.org/10.3390/rs8060518
Chicago/Turabian StyleKim, Seokhyeon, Robert M. Parinussa, Yi Y. Liu, Fiona M. Johnson, and Ashish Sharma. 2016. "Merging Alternate Remotely-Sensed Soil Moisture Retrievals Using a Non-Static Model Combination Approach" Remote Sensing 8, no. 6: 518. https://doi.org/10.3390/rs8060518
APA StyleKim, S., Parinussa, R. M., Liu, Y. Y., Johnson, F. M., & Sharma, A. (2016). Merging Alternate Remotely-Sensed Soil Moisture Retrievals Using a Non-Static Model Combination Approach. Remote Sensing, 8(6), 518. https://doi.org/10.3390/rs8060518