Content-Based High-Resolution Remote Sensing Image Retrieval via Unsupervised Feature Learning and Collaborative Affinity Metric Fusion

Abstract

With the urgent demand for automatic management of large numbers of high-resolution remote sensing images, content-based high-resolution remote sensing image retrieval (CB-HRRS-IR) has attracted much research interest. Accordingly, this paper proposes a novel high-resolution remote sensing image retrieval approach via multiple feature representation and collaborative affinity metric fusion (IRMFRCAMF). In IRMFRCAMF, we design four unsupervised convolutional neural networks with different layers to generate four types of unsupervised features from the fine level to the coarse level. In addition to these four types of unsupervised features, we also implement four traditional feature descriptors, including local binary pattern (LBP), gray level co-occurrence (GLCM), maximal response 8 (MR8), and scale-invariant feature transform (SIFT). In order to fully incorporate the complementary information among multiple features of one image and the mutual information across auxiliary images in the image dataset, this paper advocates collaborative affinity metric fusion to measure the similarity between images. The performance evaluation of high-resolution remote sensing image retrieval is implemented on two public datasets, the UC Merced (UCM) dataset and the Wuhan University (WH) dataset. Large numbers of experiments show that our proposed IRMFRCAMF can significantly outperform the state-of-the-art approaches.

1. Introduction

With the rapid development of remote sensing technology, the volume of acquired high-resolution remote sensing images has dramatically increased. The automatic management of large volumes of high-resolution remote sensing images has become an urgent problem to be solved. Among the new emerging high-resolution remote sensing image management tasks, content-based high-resolution remote sensing image retrieval (CB-HRRS-IR) is one of the most basic and challenging technologies [1]. Based on the query image provided by the data administrator, CB-HRRS-IR specifically works by searching for similar images in the high-resolution remote sensing image archives. Due to its potential applications in high-resolution remote sensing image management, CB-HRRS-IR has attracted increasing attention [2].

In the remote sensing community, conventional image retrieval systems rely on manual tags describing the sensor type, waveband information, and geographical location of remote sensing images. Accordingly, the retrieval performance of these tag-matching-based methods highly depends on the availability and quality of the manual tags. However, the creation of image tags is usually time-consuming and becomes impossible when the volume of acquired images explosively increases. Recent research has shown that the visual contents themselves are more relevant than the manual tags [3]. With this consideration, more and more researchers have started to exploit the CB-HRRS-IR technology. In recent decades, different types of CB-HRRS-IR have been proposed. Generally, existing CB-HRRS-IR methods can be classified into two categories: those that take only one single image as the query image [1,2,4,5,6,7] and those that simultaneously take multiple images as the query images [3,8]. In the latter category, multiple query images including positive and negative samples are iteratively generated during the feedback retrieval process. Accordingly, the approaches from the latter category involve multiple interactive annotations. It is noted that the approaches from the former category take only one query image as the input in one retrieval trial. To minimize the manual burden, this paper follows the style of the former category. Of the methods in the former category, all of them consist of two essential modules: the feature representation module and the feature searching module. The feature representation module extracts the feature vector from the image to describe the visual content of the image. Based on the extracted feature vectors, the feature searching module calculates the similarity values between images and outputs the most similar images by sorting the similarity values.

For charactering high-resolution remote sensing images, low-level features such as spectral features [9,10], shape features [11,12], morphological features [5], texture features [13], and local invariant features [2] have been adopted and evaluated in the CB-HRRS-IR task. Although low-level features have been employed with a certain degree of success, they have a very limited capability in representing the high-level concepts presented by remote sensing images (i.e., the semantic content). This issue is known as the semantic gap between low-level features and high-level semantic features. To narrow this gap, Zhou et al. utilized the auto-encoder model to encode the low-level feature descriptor for pursing sparse feature representation [6]. Although the encoded feature can achieve a higher retrieval precision, this strategy is limited because the re-representation approach takes the low-level feature descriptor as the input, which has lost some spatial and spectral information. As high-resolution remote sensing images are rich in complex structures, high-level semantic feature extraction is an exceptionally difficult task and a direction worthy of in-depth study.

In the feature searching module, both precision and speed are pursued. In [2], different similarity metrics for single features are systematically evaluated. Shyu et al. utilized the linear combination approach to measure the similarity when multiple features of one image are simultaneously utilized [1]. In very recent years, the volume of available remote sensing images has dramatically increased. Accordingly, the complexity of the feature searching is very high, as the searching process should access all the images in the dataset. To decrease the searching complexity, the tree-based indexing approach [1] and the hashing-based indexing approach [5] were proposed. The acceleration of the existing approaches can be implemented by the use of parallel devices, so the key problem in the feature searching module is to exploit good similarity measures.

In order to address these problems in CB-HRRS-IR, this paper proposes a novel approach using unsupervised feature learning and collaborative metric fusion. In [14], unsupervised multilayer feature learning is proposed for high-resolution remote sensing image scene classification. As depicted there, unsupervised multilayer feature learning could extract complex structure features via a hierarchical convolutional scheme. For the first time, this paper extends unsupervised multilayer feature learning to CB-HRRS-IR. Derived from unsupervised multilayer feature learning, one-layer, two-layer, three-layer, and four-layer feature extraction frameworks are constructed for mining different characteristics from different scales. In addition to these features generated via unsupervised feature learning, we also re-implement traditional features including local binary pattern (LBP) [15], gray level co-occurrence matrix (GLCM) [16], maximal response 8 (MR8) [17], and scale-invariant feature transform (SIFT) [18] in computer vision. Based on these feature extraction approaches, we can obtain a set of features for each image. Generally, different features can reflect the different characteristics of one given image and play complementary roles. To make multiple complementary features effective in CB-HRRS-IR, we utilize the graph-based cross-diffusion model [19] to measure the similarity between the query image and the test image. In this paper, the proposed similarity measure approach is named collaborative metric fusion because it can collaboratively exchange information from multiple feature spaces in the fusion process. Experimental results show that the proposed unsupervised features derived from unsupervised feature learning can achieve higher precision than the conventional features in computer vision such as LBP, GLCM, MR8, and SIFT. Benefiting from the utilized collaborative metric fusion approach, the retrieval results can be significantly improved by use of multiple features. The feature set containing unsupervised features can outperform the feature set containing conventional features, and the combination of unsupervised features and conventional features can achieve the highest retrieval precision. The main contributions of this paper are twofold:

• Unsupervised features derived from unsupervised multilayer feature learning are utilized in CB-HRRS-IR for the first time and could significantly outperform the conventional features such as LBP, GLCM, MR8, and SIFT in CB-HRRS-IR.
• In the remote sensing community, collaborative affinity metric fusion is utilized for the first time. Compared with greedy affinity metric fusion, in which multiple features are integrated and further measured by the Euclidean distance, collaborative affinity metric fusion can make the introduced complementary features more effective in CB-HRRS-IR.

This paper is organized as follows. The generation process of unsupervised features is presented in Section 2. In Section 3, collaborative affinity metric fusion is described and utilized to measure the similarity when multiple features of one image are available and simultaneously utilized for calculating the similarity. Section 4 summarizes the proposed algorithm for CB-HRRS-IR, and the overall performance of the proposed approach is presented in Section 5. Finally, Section 6 provides the conclusion of this paper.

2. Unsupervised Feature Learning

With the development of deep learning [20,21,22], the performances of many visual recognition and classification tasks have been significantly improved. However, supervised deep learning methods [23], e.g., deep convolutional neural networks (DCNN), rely heavily on millions of human-annotated data that are non-trivial to obtain. In visual recognition and classification tasks, supervised deep learning outputs class-specific feature representation via large-scale supervised learning. However, content-based high-resolution remote sensing image retrieval (CB-HRRS-IR) pursues generic feature representation. Accordingly, this paper exploits unsupervised feature learning approaches [14,24,25] to implement generic feature representation. To improve the image retrieval performance, this paper tries to extract as many complementary features as possible to depict the high-resolution remote sensing images. Accordingly, each satellite image can be expressed by one feature set that contains multiple complementary features. In the high-resolution remote sensing image scene classification task, the data-driven features derived from unsupervised multilayer feature learning [14] outperform many state-of-the-art approaches. In addition, the features from different layers of the unsupervised multilayer feature extraction network show complementary discrimination abilities. Hence, this paper utilizes unsupervised multilayer feature learning [14] to generate the feature set of each image for CB-HRRS-IR, where the feature set of one image is composed of multiple feature vectors mined from the corresponding image.

In [14], the proposed feature extraction framework contains two feature layers, and two different feature representations are extracted by implementing a global pooling operation on the first feature layer and the second feature layer of the same feature extraction network. The number of bases of the intermediate feature layer is set to a relatively small value because too large a number would dramatically increase the computation complexity and memory consumption [14]. Accordingly, the representation characteristic of the lower feature layer is not fully exploited. To overcome this drawback, this paper designs four unsupervised convolution feature extraction networks via unsupervised multilayer feature learning to fully mine the representation characteristics of different feature layers. More unsupervised convolution feature extraction networks can be similarly derived from unsupervised multilayer feature learning. Four unsupervised feature extraction networks contain one feature layer, two feature layers, three feature layers, and four feature layers, respectively. Although the layer numbers of the four unsupervised feature extraction networks are different, any unsupervised feature extraction network includes three basic operations: (1) the convolutional operation; (2) the local pooling operation; and (3) the global pooling operation. In addition, each feature layer contains one convolution operation and one local pooling operation, as illustrated in Figure 1 and Figure 2.

More specifically, convolutional operation works for feature mapping, which is constrained by the function bases (i.e., the convolutional templates). In addition, the function bases are generated by unsupervised K-means clustering. Local pooling operation works to keep the layer invariant to slight translation and rotation and is implemented by the traditional calculation process (i.e., the local maximum). Generally, the global pooling operation is implemented by sum-pooling in multiple large windows [14,25], and multiple sum-pooling results are integrated as a feature vector. For simplifying the computational complexity and improving the rotation invariance, global pooling in this paper is implemented by sum-pooling in the whole window. The global pooling result (i.e., the feature representation) $\mathit{f}\in R^K$ can be formulated as

$${\mathit{f}}_k=\frac{{\displaystyle {\sum }_{i,j}\mathit{R}(i,j,k)}}{H\times W},k=1,2,\cdots ,K,$$

(1)

where $\mathit{R}\in R^{H\times W\times K}$ denotes the local pooling result of the last layer. In addition, $H$, $W$, and $K$ denote the height, the width, and the depth of $\mathit{R}$.

In order to facilitate the understanding of the feature extraction framework, feature extraction networks with one feature extraction layer and two feature extraction layers are visually illustrated in Figure 1 and Figure 2. Through stacking convolution operations and local pooling operations, the feature extraction networks with three feature extraction layers and four feature extraction layers can be analogously constructed.

In our implementation, the numbers of bases of the different feature layers in each feature extraction network are specifically demonstrated in the following. As depicted in [14], the more bases that the intermediate feature layers have, the better the performance of the generated feature. However, more bases would remarkably increase the computational complexity. To achieve a balance between performance and complexity, the number of bases is set to a relatively small value in the following. For the feature extraction network with one feature extraction layer, the number of bases of the first layer is 1024. For the feature extraction network with two feature extraction layers, the number of bases in the first layer is 100, and the number of bases in the second layer is 1024. For the feature extraction network with three feature extraction layers, the number of bases in the first layer is 64, the number of bases in the second layer is 100, and the number of bases in the third layer is 1024. For the feature extraction network with four feature extraction layers, the number of bases in the first layer is 36, the number of bases in the second layer is 64, the number of bases in the third layer is 100, and the number of bases in the fourth layer is 1024. Other parameters such as the receptive field and the local window size of the local pooling operation are set according to [14].

As depicted in [14], the bases of the aforementioned unsupervised convolution feature extraction networks can be learnt via layer-wise unsupervised learning. Once the parameters of the aforementioned four feature extraction networks are determined, the four different feature extraction networks can be used for feature representation. Given one input remote sensing image, we can obtain four different types of features via the four feature extraction networks. In the following, the four different types of features represented by the introduced four Unsupervised Convolutional Neural Networks with one feature layer, two feature layers, three feature layers, and four feature layers are abbreviated as UCNN1, UCNN2, UCNN3, and UCNN4, respectively.

As mentioned, the feature extraction pipeline of these neural networks is fully learned from unlabeled data. The size and band of the input image are highly flexible. Hence, this unsupervised feature learning approach can be easily extended to different types of remote sensing image without any dimension reduction of the bands.

In addition to UCNN1, UCNN2, UCNN3, and UCNN4, we re-implement the conventional feature descriptors in computer vision, including LBP [15], GLCM [16], MR8 [17], and SIFT [18], which are taken as the baselines for comparison. In the extraction process of the LBP feature, the uniform rotation-invariant feature is computed by 16 sampling points on a circle with a radius equal to 3. The LBP feature is generated through quantifying the uniform rotation-invariant features under the constraint of the mapping tables with 36 patterns. The GLCM feature encodes the contrast, the correlation, the energy, and the homogeneity along three offsets (i.e., 2, 4, and 6). The MR8 and SIFT features are histogram features using the bag of visual words model, and the volume of the visual dictionary is set to 1024.

As demonstrated in

Table 1. Feature set for representing high-resolution remote sensing images.

Feature Type	Feature Dimension
LBP in [15]	36
GLCM in [16]	12
MR8 in [17]	1024
SIFT in [18]	1024
UCNN1	1024
UCNN2	1024
UCNN3	1024
UCNN4	1024

, conventional features including LBP, GLCM, MR8, and SIFT and unsupervised convolution features including UCNN1, UCNN2, UCNN3, and UCNN4 constitute the feature set for comprehensively depicting and indexing the remote sensing image. Features from this feature set are utilized to implement high-resolution remote sensing image retrieval via collaborative metric fusion, as is specifically introduced in Section 3.

3. Collaborative Affinity Metric Fusion

In Section 2, we introduce unsupervised features derived from unsupervised multilayer feature learning and review several conventional feature extraction approaches in computer vision. The content of each high-resolution remote sensing image can be depicted by a set of feature representations using the aforementioned feature extraction approaches. In addition, the affinity of two images can be measured by the similarity of their corresponding feature representations. Although more feature representations intuitively benefit measuring the similarity between two images, how to effectively measure the similarity is still a challenging task when multiple features are available. With this consideration, this section introduces collaborative affinity metric fusion to measure the similarity of two images when each image is represented by multiple features. To address the superiority of collaborative affinity metric fusion, this section first describes greedy affinity metric fusion.

To facilitate clarifying and understanding the affinity metric fusion methods, the adopted feature set is first demonstrated. Assuming that the adopted feature set contains $M$ types of features, the feature set of the $\alpha$-th high-resolution remote sensing image can be formulated as $\mathit{S}(\alpha )=\left\{{\mathit{f}}^1(\alpha ),{\mathit{f}}^2(\alpha ),\cdots ,{\mathit{f}}^M(\alpha )\right\}$, where ${\mathit{f}}^m(\alpha )\in R^{D(m)}$ denotes the vector of the $m$-th type of feature and $D(m)$ denotes the dimension of the $m$-th type of feature.

3.1. Greedy Affinity Metric Fusion

In the literature, when an image is represented by only one type of feature, the dissimilarity between two images can be easily calculated by the Euclidean distance or other metrics [2], and the affinity between two images can be further achieved. In this paper, one image is represented by one feature set that contains multiple types of features. Although the representations of the images become richer, how to robustly measure the affinity between images becomes more difficult.

Here, we first present a plain approach (i.e., greedy affinity metric fusion) to combine multiple features to measure the affinity between images. More specifically, multiple features from the feature set can be first integrated as a super feature vector, and the distance between two feature sets can be greedily calculated by the Euclidean distance between two super feature vectors. Before the features are integrated, each type of feature is first normalized. For conciseness, we only introduce the normalization process of one type of feature, in which each dimension of the feature has the mean value subtracted from it and is further divided by the standard deviation. In addition, the feature is divided by its dimension to reduce the dimension influence of the different types of features.

In this paper, the Euclidean distance is adopted for the primary attempt, and more metrics will be tested in future work. The formulation of greedy affinity metric fusion is as follows. Given the $\alpha$-th and $\beta$-th high-resolution remote sensing images, the super feature vectors can be expressed by $\mathit{F}(\alpha )=[{\mathit{f}}^1(\alpha ),{\mathit{f}}^2(\alpha ),\cdots ,{\mathit{f}}^M(\alpha )]$ and $\mathit{F}(\beta )=[{\mathit{f}}^1(\beta ),{\mathit{f}}^2(\beta ),\cdots ,{\mathit{f}}^M(\beta )]$, where $\mathit{F}(\alpha )\in R^{D(1)+D(2)+\cdots +D(M)}$ and $\mathit{F}(\beta )\in R^{D(1)+D(2)+\cdots +D(M)}$. The affinity between the $\alpha$-th and $\beta$-th high-resolution remote sensing images can be expressed by

$$Af{f}^{GAMF}(\alpha ,\beta )=\exp \left(\frac{\left|\right|\mathit{F}(\alpha )-\mathit{F}(\beta )|{|}_2}{{\sigma }_{\mathit{F}}}\right),$$

(2)

where $\left|\right|\cdot |{|}_2$ denotes the Euclidean distance or the L2 distance [2], and ${\sigma }_{\mathit{F}}$ is the control constant.

Although greedy metric fusion can utilize multiple features to calculate the similarity between images, its use would be not ideal when the super feature vectors in Equation (2) are highly hybrid [26]. Accordingly, how to fully incorporate the merit of multiple features for measuring the affinity between two images deserves more explanation.

3.2. Collaborative Affinity Metric Fusion

For greedy affinity metric fusion, the affinity calculation of two high-resolution remote sensing images considers only the images themselves. However, the affinity calculation can be improved by importing other auxiliary images in the image dataset. Greedy affinity metric fusion also suffers from the weakness that the Euclidean distance is unsuitable when the super feature vector is highly hybrid. With this consideration, this section introduces collaborative affinity metric fusion to address these problems. Collaborative affinity metric fusion originates from the self-smoothing operator [27], which can robustly measure the affinity by propagating the similarities among auxiliary images when only one type of feature is utilized and is fully proposed in [19] for natural image retrieval by fusing multiple metrics. Afterwards, collaborative affinity metric fusion is utilized in genome-wide data aggregation [28] and multi-cue fusion for salient object detection [29]. In this paper, we utilize collaborative affinity metric fusion to fully incorporate the merit of multiple features introduced in Section 2 for content-based high-resolution remote sensing image retrieval (CB-HRRS-IR).

3.2.1. Graph Construction

As depicted in [19], collaborative affinity metric fusion is based on multiple graphs. As mentioned, the adopted feature set is assumed to contain $M$ types of features. Here, the number of graphs is equal to $M$, and each graph can be constructed from one type of feature in the feature set, using an image dataset that is assumed to contain $N$ images.

For the $m$-th feature, the corresponding full graph is expressed by ${\mathit{G}}^m=\left\{{\mathbf{V}}^m,{\mathbf{E}}^m,{\mathbf{W}}^m\right\}$, where ${\mathbf{V}}^m=\left\{1,2,\cdots ,N\right\}$ stands for the node set, ${\mathbf{E}}^m\subseteq {\mathbf{V}}^m\times {\mathbf{V}}^m$ is the edge set, and ${\mathbf{W}}^m\in R^{N\times N}$ denotes the affinity matrix. Using the $m$-th feature, ${\mathrm{W}}_{i,j}^m$ denotes the similarity or affinity value between the $i$-th node (i.e., the $i$-th image) and the $j$-th node (i.e., the $j$-th image) and can be formulated as

$${\mathrm{W}}_{i,j}^m=\exp \left(\frac{\left|\right|{\mathit{f}}^m(i)-{\mathit{f}}^m(j)|{|}_2}{{\sigma }_f^m}\right),$$

(3)

where ${\sigma }_f^m$ is the control constant, which is the median value of the distances of two arbitrary feature vectors.

By normalizing ${\mathbf{W}}^m$ along each row, we can get the status matrix ${\mathbf{P}}^m$, which is defined by

$${\mathrm{P}}_{i,j}^m=\frac{{{W}}_{i,j}^m}{{\displaystyle {\sum }_{j\in {\mathbf{V}}^m}{\mathrm{W}}_{i,j}^m}}.$$

(4)

Given the fully connected graph ${\mathit{G}}^m=\left\{{\mathbf{V}}^m,{\mathbf{E}}^m,{\mathbf{W}}^m\right\}$, we can construct the locally connected graph ${\tilde{\mathit{G}}}^m=\left\{{\tilde{\mathbf{V}}}^m,{\tilde{\mathbf{E}}}^m,{\tilde{\mathbf{W}}}^m\right\}$. ${\tilde{\mathit{G}}}^m$ has the same node set as ${\mathit{G}}^m$ (i.e., ${\mathbf{V}}^m={\tilde{\mathbf{V}}}^m$). However, different from ${\mathit{G}}^m$, each node of ${\tilde{\mathit{G}}}^m$ is only locally connected with its $L$ nearest neighboring nodes, that is, $(i,j)\in {\tilde{\mathbf{E}}}^m$ if and only if $j\in \Omega (i)$, where $\Omega (i)$ denotes the neighboring node set of the $i$-th node. In addition, the local affinity matrix ${\tilde{\mathbf{W}}}^m$ can be defined by

$${\tilde{\mathrm{W}}}_{i,j}^m=\{\begin{array}{cc}{\mathrm{W}}_{i,j}^m,& ifj\in \Omega (i)\\ 0,& otherwise\end{array}.$$

(5)

By normalizing ${\tilde{\mathbf{W}}}^m$ along each row, the kernel matrix ${\tilde{\mathbf{P}}}^m$ can be formulated as

$${\tilde{\mathrm{P}}}_{i,j}^m=\frac{{\tilde{\mathrm{W}}}_{i,j}^m}{{\displaystyle {\sum }_{j\in \Omega (i)}{\tilde{\mathrm{W}}}_{i,j}^m}}.$$

(6)

It is noted that the status matrix ${\mathbf{P}}^m$ carries the affinity information in the global domain among graph nodes, while the kernel matrix ${\tilde{\mathbf{P}}}^m$ encodes the local affinity information in the local domain among graph nodes. Replicating the above steps, we can similarly construct $M$ fully connected graphs ${\mathit{G}}^1,{\mathit{G}}^2,\cdots ,{\mathit{G}}^M$ and $M$ locally connected graphs ${\tilde{\mathit{G}}}^1,{\tilde{\mathit{G}}}^2,\cdots ,{\tilde{\mathit{G}}}^M$.

3.2.2. Affinity Metric Fusion via Cross-Diffusion

Supposing that $M$ fully connected graphs ${\mathit{G}}^1,{\mathit{G}}^2,\cdots ,{\mathit{G}}^M$ and $M$ locally connected graphs ${\tilde{\mathit{G}}}^1,{\tilde{\mathit{G}}}^2,\cdots ,{\tilde{\mathit{G}}}^M$ have been constructed, this section introduces the generation process of the fused affinity matrix ${\mathbf{W}}^{FAM}$. Before giving the final fused affinity matrix ${\mathbf{W}}^{FAM}$, we first give the cross-diffusion formulation,

$${\mathbf{P}}^m(t)=\left({\tilde{\mathbf{P}}}^m\right)\times \left(\frac{1}{M-1}{\displaystyle \sum _{k\ne m}{\mathbf{P}}^k(t-1)}\right)\times {\left({\tilde{\mathbf{P}}}^m\right)}^{\mathrm{T}}+\eta \mathbf{I}$$

(7)

where $m=1,2,\cdots ,M$, $t=1,2,\cdots ,T$, ${\mathbf{P}}^m(0)$ denotes the original status matrix ${\mathbf{P}}^m$, ${\mathbf{P}}^m(t)$ is the diffusion result at the $t$-th iteration step, $\mathbf{I}$ is an identity matrix, and $\eta >0$ is a scalar regularization penalty that works to avoid the loss of self-similarity through the diffusion process and benefits achieving consistency and convergence in different tasks [19]. Previous studies [29] have shown that the values of the iteration step $T$ and the regularization penalty $\eta$ are not sensitive to the final results. Hence, in this paper, $T$ and $\eta$ are empirically set to 20 and 1.

In the above cross-diffusion process, ${\tilde{\mathbf{P}}}^m,m=1,2,\cdots ,M$ and ${\mathbf{P}}^m(0)={\mathbf{P}}^m,m=1,2,\cdots ,M$ are taken as the original inputs. After one iteration, ${\mathbf{P}}^m(1),m=1,2,\cdots ,M$ can be calculated via Equation (7). In addition, ${\mathbf{P}}^m(2),m=1,2,\cdots ,M$, ${\mathbf{P}}^m(3),m=1,2,\cdots ,M$, and ${\mathbf{P}}^m(T),m=1,2,\cdots ,M$ can be successively calculated.

Generally, the success of the diffusion process in Equation (7) benefits from the constraint of the kernel matrices ${\tilde{\mathbf{P}}}^m,m=1,2,\cdots ,M$, which are locally connected. In the kernel matrices, only nodes with high reliability are connected, which makes the diffusion process robust to the noise of similarity measures in the fully connected graph. In addition, the diffusion process in Equation (7) is implemented across graphs that are constructed of different types of features. This makes the diffusion process incorporate the complementary merit of different features.

The fused affinity matrix ${\mathbf{W}}^{FAM}$ can be expressed by the average of the cross-diffusion results of the status matrices after $T$ iterations:

$${\mathbf{W}}^{FAM}=\frac{1}{M}{\displaystyle \sum _{m=1}^M{\mathbf{P}}^m(T)},$$

(8)

where ${\mathbf{P}}^m(T)$ is the final cross-diffusion result of the status matrix that corresponds to the $m$-th type of feature. It is noted that ${\mathbf{P}}^m(T)$ incorporates information from other types of features in the diffusion process, as depicted in Equation (7).

Finally, the affinity value between the $\alpha$-th and $\beta$-th high-resolution remote sensing images in the image dataset can be expressed by

$$Af{f}^{CAMF}(\alpha ,\beta )={\mathrm{W}}_{\alpha ,\beta }^{FAM},$$

(9)

where ${\mathrm{W}}^{FAM}$ is the cross-diffusion result of Equation (7). In ${\mathrm{W}}^{FAM}$, the similarity between two arbitrary nodes (i.e., the images) is the diffusion result with the aid of auxiliary nodes (i.e., auxiliary images).

As a whole, compared with greedy affinity metric fusion, collaborative affinity metric fusion can not only propagate the affinity values among auxiliary images for improving the affinity calculation of two images of interest, but can also flexibly incorporate the merit of multiple features.

4. Image Retrieval via Multiple Feature Representation and Collaborative Affinity Metric Fusion

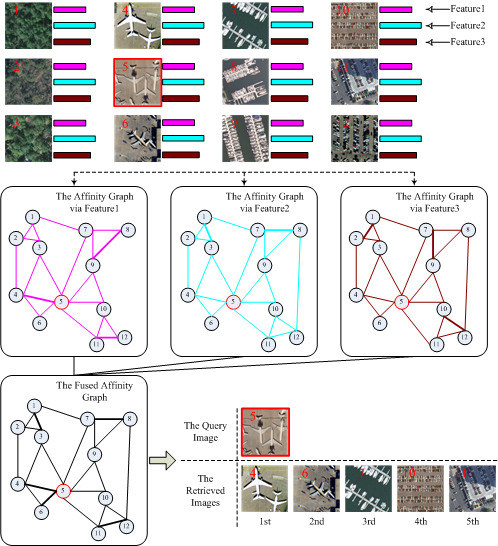
As mentioned, this paper proposes a robust high-resolution remote sensing Image Retrieval approach via Multiple Feature Representation and Collaborative Affinity Metric Fusion, which is called IRMFRCAMF in the following. The main processing procedures of our proposed IRMFRCAMF are visually illustrated in Figure 3. As depicted, each high-resolution remote sensing image is represented by multiple types of features. Using each type of feature, one fully connected graph and one corresponding locally connected graph are constructed. Furthermore, we can achieve a fused graph by implementing a cross-diffusion operation on all of the constructed graphs. From the fused graph, we can obtain an affinity value between two nodes that directly reflects the affinity between two corresponding images. Accordingly, we can easily finish the image retrieval task after achieving the affinity values between the query image and the other images in the image dataset.

With the consideration that Figure 3 only gives a simplified exhibition of our proposed IRMFRCAMF, to deeply demonstrate our proposed IRMFRCAMF, the generalized description of our proposed IRMFRCAMF is specifically introduced in the following. Corresponding to the aforementioned definitions, the image dataset is assumed to contain $N$ images, and each image is assumed to be represented by $M$ types of features. Accordingly, $N$ images can be represented by $N$ feature sets $\mathit{S}(i)=\left\{{\mathit{f}}^1(i),{\mathit{f}}^2(i),\cdots ,{\mathit{f}}^M(i)\right\},i=1,2,\cdots ,N$. Furthermore, $M$ fully connected graphs ${\mathit{G}}^m=\left\{{\mathbf{V}}^m,{\mathbf{E}}^m,{\mathbf{W}}^m\right\},m=1,2,\cdots ,M$ can be constructed, and ${\mathit{G}}^m=\left\{{\mathbf{V}}^m,{\mathbf{E}}^m,{\mathbf{W}}^m\right\}$ is constructed using the features sets ${\mathit{S}}^m(i)=\left\{{\mathit{f}}^m(i)\right\},i=1,2,\cdots ,N$. Let $L$ denote the number of nearest neighboring nodes, and $M$ locally connected graphs ${\tilde{\mathit{G}}}^m=\left\{{\tilde{\mathbf{V}}}^m,{\tilde{\mathbf{E}}}^m,{\tilde{\mathbf{W}}}^m\right\},m=1,2,\cdots ,M$ can be correspondingly constructed. Let the $q$-th image in the image dataset denote the query image, and the most related images can be automatically accurately retrieved using our proposed IRMFRCAMF, which is elaborately described in Algorithm 1.

In many applications, such as image management in a local repository, the volume of the image dataset is fixed over a period of time, and the query image also comes from the image dataset. In this case, the features of images can be calculated in advance, and the affinity matrix calculation can be performed as an offline process. Accordingly, the image retrieval task can be instantaneously completed just through searching the affinity matrix.

However, the volume of the image dataset may be increased after a long time, and the query image may not be from the image dataset. Even in this extreme circumstance, the existing features of the images in the original dataset can be reused, but the affinity matrix should be recalculated. To facilitate the evaluation of the time cost of data updating, we provide the computational complexity of the affinity matrix calculation process in the following. The complexity of constructing $M$ fully connected graphs is $O(M{N}^2)$, where $N$ is the volume of the dataset. As depicted in Section 3.2.1, searching $L$ nearest neighbors for each feature vector is the premise for constructing locally connected graphs. In addition, the time complexity of searching $L$ nearest neighbors for each feature vector is close to $O((L+N)\log N)$ by using the k-d tree [30], and the complexity of constructing $M$ locally connected graphs is close to $O(MNL\log N+M{N}^2\log N)$. The complexity of the cross-diffusion process in Section 3.2.2 is $O(TM{N}^3)$, where $T$ is the iteration number in the cross-diffusion process. The total complexity of the affinity matrix calculation is $O(M{N}^2+MNL\log N+M{N}^2\log N+TM{N}^3)$, and the primary complexity is introduced by the cross-diffusion process. The time cost of the affinity matrix calculation is mainly influenced by the volume of the image dataset.

Algorithm 1. High-resolution remote sensing image retrieval via multiple feature representation and collaborative affinity metric fusion.

Input: the high-resolution remote sensing image dataset that contains $N$ images; the query image (i.e., the $q$-th image); the number of nearest neighboring nodes $L$; other parameters set according to [19].

1. Calculate the feature sets $\mathit{S}(i)=\left\{{\mathit{f}}^1(i),{\mathit{f}}^2(i),\cdots ,{\mathit{f}}^M(i)\right\},i=1,2,\cdots ,N$ according to the feature extraction approaches defined in Section 2.

2. Construct the fully connected graphs ${\mathit{G}}^m=\left\{{\mathbf{V}}^m,{\mathbf{E}}^m,{\mathbf{W}}^m\right\},m=1,2,\cdots ,M$ and the locally connected graphs ${\tilde{\mathit{G}}}^m=\left\{{\tilde{\mathbf{V}}}^m,{\tilde{\mathbf{E}}}^m,{\tilde{\mathbf{W}}}^m\right\},m=1,2,\cdots ,M$ using the extracted feature sets according to Section 3.2.1.

3. Calculate the fused affinity matrix ${\mathbf{W}}^{FAM}$ using the constructed graphs via cross-diffusion according to Section 3.2.2.

4. Generate the affinity vector $\left[{\mathrm{W}}_{q,1}^{FAM},{\mathrm{W}}_{q,2}^{FAM},\cdots ,{\mathrm{W}}_{q,N}^{FAM}\right]$ that records the affinity values between the query image and the other images in the image dataset.

5. Get the indexes of the most related images by ranking the affinity vector $\left[{\mathrm{W}}_{q,1}^{FAM},{\mathrm{W}}_{q,2}^{FAM},\cdots ,{\mathrm{W}}_{q,N}^{FAM}\right]$ in descending order.

Output: the most related images.

5. Experimental Results

In this section, we first introduce two adopted evaluation datasets and criteria that are specifically introduced in Section 5.1. Section 5.2 demonstrates the first evaluation dataset, analyzes the sensitivity of the crucial parameters of the proposed approach, and provides a comparison of the results with those of state-of-the-art approaches. Based on the parameter configuration that is tuned on the first dataset, for pursuing general applicability, the proposed approach is directly compared with state-of-the-art approaches on the second evaluation dataset. Section 5.3 reports the comparison results on the second dataset.

5.1. Evaluation Dataset and Criteria

In the following, the adopted evaluation dataset and evaluation criteria are presented.

5.1.1. Evaluation Dataset

In this paper, we perform the quantitative evaluation of the high-resolution remote sensing image retrieval performance using two publicly available datasets, the UC Merced (UCM) dataset [31,32] and the Wuhan University (WH) dataset [33]. The UCM dataset has been widely utilized in the performance evaluation of high-resolution remote sensing image retrieval [2,3,4,5,6] and high-resolution remote sensing image scene classification [14,25,31,32,34,35,36,37,38,39,40]. More specifically, the UCM dataset is generated through manually labeling aerial image blocks of large images from the USGS national map urban area imagery. The UCM dataset comprises 21 land cover categories. Each class contains 100 images with 256 × 256 pixels, the spatial resolution of each pixel is 30 cm, and each pixel is measured in the RGB spectral space. The WH dataset is created by labeling satellite image blocks from Google Earth by Wuhan University. It has been widely utilized in the remote sensing image scene classification task [33,40,41,42,43]. The WH dataset comprises 19 land cover categories, each class contains 50 images with 600 × 600 pixels, and each pixel is measured in the RGB spectral space.

The UCM dataset contains 21 categories, and the WH dataset contains 19 categories. However, both of them may end up not 1:1 with real world physical categories. For example, in reality, remote sensing images are covered by clouds. In order to address real applications, the cloudy scene can be taken as a new category that is supplementary to the existing categories addressed in the datasets. If readers are interested in the retrieval task for a larger remote sensing image such as one whole satellite image, the large remote sensing image can be first cut into homogeneous scenes of a suitable size. This processing procedure is described in [44]. In this paper, we mainly focus on exploiting feature representations and metric fusion methods. As a primary attempt, the proposed approach is tested on two public datasets. In our future work, the proposed approach would be evaluated on the basis of more data.

5.1.2. Evaluation Criteria

This paper uses the popular retrieval precision [6,8] to evaluate the performance of the image retrieval approaches. As the two adopted evaluation datasets comprise multiple classes, both the class-level precision (CP) and the dataset-level precision (DP) are adopted and defined as follows.

The average retrieval precision of the $c$-th class can be expressed by

$${\mathrm{CP}}_c=\frac{{\displaystyle {\sum }_{y=1}^Y{\mathrm{CP}}_c^y}}{Y},$$

(10)

where ${\mathrm{CP}}_c^y$ denotes the retrieval precision when one query image is randomly selected from the $c$-th class and the top 10 images are taken as the retrieval results. More specifically, the retrieval precision can be expressed by $n/10$, where $n$ is the number of the top 10 retrieved images belonging to the class of the query image. For each class, we repeat the above retrieval experiment $Y$ times. In our implementation, $Y$ is set to 10.

If the adopted evaluation dataset contains $C$ classes, the overall precision $DP$ can be expressed by

$$\mathrm{DP}=\frac{{\displaystyle {\sum }_{c=1}^C{\mathrm{CP}}_c}}{C}$$

(11)

As a whole, $\mathrm{CP}$ not only depicts the retrieval performance of each class, but reflects the variation of the retrieval precision across different classes. $\mathrm{DP}$ can indicate the overall retrieval performance of one image retrieval approach.

5.2. Experiments on UCM Dataset

As mentioned, the UCM dataset comprises 21 land cover categories, and each class contains 100 images. Figure 4 shows four random images from each class in this dataset. For conciseness, the agricultural class, the airplane class, the baseball diamond class, the beach class, the buildings class, the chaparral class, the dense residential class, the forest class, the freeway class, the golf course class, the harbor class, the intersection class, the medium residential class, the mobile home park class, the overpass class, the parking lot class, the river class, the runway class, the sparse residential class, the storage tanks class, and the tennis courts class are abbreviated by the 1st–21st classes, respectively.

5.2.1. Comparisons among Different Single Features

In order to test the respective contribution of each type of feature introduced in Section 2, this section implements the remote sensing image retrieval experiment using each single feature. The L1 and L2 distances are taken as the distance metric in all of these single features. In addition, the histogram intersection distance, which is abbreviated by Intersection in the following, is also taken as a distance metric for the histogram features. The quantitative performance evaluation results are summarized in

Table 2. Dataset-level precision (DP) using different single features.

	LBP in [15]	GLCM in [16]	MR8 in [17]	SIFT in [18]	UCNN1	UCNN2	UCNN3	UCNN4
L1	0.5390	0.3152	0.5386	0.5390	0.5958	0.6157	0.5914	0.5533
L2	0.4738	0.3138	0.4419	0.3829	0.5990	0.6248	0.5929	0.5600
Intersection			0.5381	0.5390

.

Table 2 summarizes the dataset-level precisions when different single features are adopted in the image retrieval experiment. As depicted, for conventional features including LBP, GLCM, MR8, and SIFT, the L1 distance and the histogram intersection distance can achieve better retrieval performance than the L2 distance. However, the L2 distance can make the proposed unsupervised features achieve better performance than the L1 distance. As a whole, the proposed unsupervised features including UCNN1, UCNN2, UCNN3, and UCNN4 can significantly outperform the conventional feature extraction approaches including LBP, GLCM, MR8, and SIFT. Among these unsupervised features, UCNN2 can achieve the best performance. However, that does not mean that the other features are useless. Actually, these features are complementary, which is verified in the following experiment.

Hence, this positive experimental result shows the superiority of the proposed unsupervised features in the content-based high-resolution remote sensing image retrieval task.

5.2.2. Comparisons among Different Feature Combinations

In the unified framework of our proposed IRMFRCAMF, different feature combinations are tested for demonstrating the complementary characteristics of the introduced features. The feature combinations and their corresponding abbreviations are shown in

Table 3. Exploited feature combinations.

Abbreviation	Feature Combination
FC1	UCNN1 + UCNN2
FC2	UCNN1 + UCNN2 + UCNN3
FC3	UCNN1 + UCNN2 + UCNN3 + UCNN4
FC4	LBP + GLCM + MR8 + SIFT
FC5	FC3 + FC4

. Based on these feature combinations, our proposed IRMFRCAMF is configured and evaluated.

Using different feature combinations, the class-level precisions and the data-level precisions are summarized in Figure 5 and

Table 4. Dataset-level precision (DP) using different feature combinations.

	FC1	FC2	FC3	FC4	FC5
DP	0.6619	0.6743	0.6867	0.6586	0.7657

. As depicted in Figure 5, the comparison among FC1, FC2, and FC3 reflects that the unsupervised features from different layers are complementary, and the use of more features improves the image retrieval performance. The comparison between FC3 and FC4 shows that the combination of UCNN1, UCNN2, UCNN3, and UCNN4 can achieve more stable image retrieval performance than the combination of LBP, GLCM, MR8, and SIFT across 21 classes. The comparison among FC3, FC4, and FC5 reflects that the proposed unsupervised features (i.e., FC3) and the conventional features (i.e., FC4) are also complementary.

The dataset-level precision also verifies the above statement. As demonstrated in Table 4, the combination of the proposed unsupervised features (i.e., FC3) can achieve higher dataset-level precision than the combination of the conventional features (i.e., FC4). Furthermore, the combination of all the features from the feature set introduced in Section 2 can achieve the best remote sensing image retrieval performance.

5.2.3. Comparisons Using Different Affinity Metric Fusion Methods

To show the superiority of the advocated collaborative affinity metric fusion (CAMF), this section provides a quantitative comparison between CAMF and greedy affinity metric fusion (GAMF), introduced in Section 3.1. Using the feature combinations FC3, FC4, and FC5 utilized in Section 5.3, GAMF and CAMF are utilized to generate remote sensing image retrieval approaches. The newly generated approaches are shown in

Table 5. Combination methods.

Abbreviation	Feature Combination	Fusion Method
GAMF1	FC4	GAMF
CAMF1	FC4	CAMF
GAMF2	FC3	GAMF
CAMF2	FC3	CAMF
GAMF3	FC3 + FC4	GAMF
CAMF3	FC3 + FC4	CAMF

, and their evaluation results are summarized in Figure 6 and

Table 6. Dataset-level precision (DP) using different affinity metric fusion methods.

	GAMF1	CAMF1	GAMF2	CAMF2	GAMF3	CAMF3
DP	0.5476	0.6586	0.6471	0.6867	0.6648	0.7657

.

As depicted in Figure 6, for the overwhelming majority of classes, CAMF can achieve higher class-level precision than GAMF when the same feature combination is adopted.

The above statement can be intuitively verified by the dataset-level precision in Table 6. A further comparison between Table 2 and Table 6 shows that GAMF has mined the complementary information from the adopted features and achieved better performance than any single feature, while the advocated CAMF can more effectively mine the information from multiple complementary features than GAMF.

5.2.4. Number Selection of the Nearest Neighbor Nodes

In CAMF, one critical parameter existing between the fully connected graphs and the locally connected graphs is the number of nearest neighbor nodes $L$. The retrieval performance of our proposed IRMFRCAMF depends on $L$. To determine the appropriate $L$, the evaluation results of our proposed IRMFRCAMF under different $L$ are summarized in Figure 7 and

Table 7. Dataset-level precision (DP) under different numbers of nearest neighbor nodes.

	L = 25	L = 50	L = 75	L = 100
DP	0.7381	0.7462	0.7657	0.7281

.

As depicted in Figure 7, $L=50$ and $L=100$ can make our proposed IRMFRCAMF achieve the best performance for several classes, while $L=75$ can make our proposed IRMFRCAMF achieve the best performance for most classes. Furthermore, as depicted in Table 7, $L=75$ can make our proposed IRMFRCAMF achieve the highest dataset-level precision. Hence, the number of nearest neighboring nodes $L$ is set to 75 in our implementation.

5.2.5. Comparisons with Other Existing Approaches

In order to facilitate comparisons, we re-implement two existing high-resolution remote sensing image retrieval approaches, including image retrieval via local invariant features (LIF) in [2] and image retrieval via the unsupervised feature learning framework (UFLF) in [6]. In the implementation of LIF, SIFT is taken as the feature, and the L1 distance, the L2 distance, and the histogram intersection distance are taken as the distance measures. In UFLF, the unsupervised feature mined from the low-level feature via a three-layer auto-encoder is taken as the feature, and the L1 distance and L2 distance are taken as the distance measures. A quantitative comparison of the results among LIF + L1, LIF + L2, LIF+Intersection, UFLF + L1, UFLF + L2, and our IRMFRCAMF is summarized in Figure 8 and

Table 8. Dataset-level precision (DP) under different methods.

	LIF + L1 in [2]	LIF + L2 in [2]	LIF + Intersection in [2]	UFLF + L1 in [6]	UFLF + L2 in [6]	Ours IRMFRCAMF
DP	0.5390	0.3829	0.5390	0.4595	0.4329	0.7657

.

As depicted in Figure 8, the L2 distance can make UFLF outperform LIF for the majority of classes. However, LIF can achieve better performance than UFLF when the L1 distance and the histogram intersection distance are utilized. Except for the 6th class, the 9th class, and 16th class, our proposed IRMFRCAMF can dramatically outperform the existing LIF and UFLF. Furthermore, Table 8 shows that our proposed IRMFRCAMF can achieve the best dataset-level precision.

In addition to the aforementioned quantitative comparisons, we provide some visual comparisons among LIF + L1, LIF + L2, LIF + Intersection, UFLF + L1, UFLF + L2, and our IRMFRCAMF. In the following, Figure 9 and Figure 10 visually show the retrieval results of these methods. Figure 9 shows the retrieval results on the river class, which comes from a multiple texture-based scene. Given one random query image from the river class, the retrieval results using different methods are illustrated. Based on intuitive comparisons among the different methods, we can easily see that our proposed IRMFRCAMF can achieve the best retrieval performance on the river class. Because our proposed IRMFRCAMF utilizes multiple features to represent one image, our proposed IRMFRCAMF is competent at image retrieval from the multiple texture based scene. Figure 10 shows the retrieval results for the airplane class, which comes from a salient target based scene. Given one random query image from the airplane class, the retrieval results using different methods are illustrated in Figure 10. Based on intuitive comparisons among the different methods, we can easily see that our proposed IRMFRCAMF can achieve the best retrieval performance for the airplane class. The retrieval results intuitively show that our proposed IRMFRCAMF can perfectly cope with image retrieval from a salient target based scene.

As a whole, our proposed IRMFRCAMF can significantly outperform the existing methods, including LIF and MFLF, in terms of the class-level precision and the dataset-level precision. This statement can be verified by the aforementioned quantitative and qualitative comparisons.

In the following, we report the running times of the different stages of our proposed approach and other methods. All approaches are implemented on a personal computer with 3.4 GHz CPU and 16 GB RAM. The training times of the four unsupervised convolutional neural networks (i.e., UCNN) that were previously mentioned in Section 2 are reported in

Table 9. Training time of the proposed unsupervised feature learning neural networks.

	UCNN with One Feature Layer	UCNN with Two Feature Layers	UCNN with Three Feature Layers	UCNN with Four Feature Layers
Times (s)	32.529	1480.166	2868.917	2994.689

. As depicted, the more feature layers that the UCNN has, the more time needed to run the training module. It is noted that the training process works in the offline stage for outputting the feature extraction networks and is not needed in the online image retrieval stage. Accordingly, the training time does not influence the timeliness of the retrieval.

Once the unsupervised convolutional neural networks are trained, the feature representation of the image scenes can be autonomously generated by implementing the operations of the trained unsupervised convolutional neural networks. The feature extraction times of different features including the existing features are reported in

Table 10. Feature extraction times of different single features per image scene.

	LIF in [2]	UFLF in [6]	UCNN1	UCNN2	UCNN3	UCNN4
Code Type	C++	C++	Matlab	Matlab	Matlab	Matlab
Times (s)	0.062	0.071	2.231	24.663	15.513	7.682

. When a UCNN is composed of multiple feature layers, the base number of each feature layer directly influences the feature extraction complexity, and a larger number of bases in the initial feature layer tends to increase the feature extraction complexity. For examples, the feature extraction time of UCNN2 is longer than that of UCNN3 or UCNN4. As depicted in Table 10, the extraction time of our proposed unsupervised features is longer than that of LIF [2] or UFLF [6]. The features can be extracted in advance and saved in the database, and the feature representation can be directly utilized in the retrieval stage. With this consideration, the high complexity of the feature extraction is still acceptable in the retrieval task. Furthermore, the extraction process of the proposed unsupervised features can be accelerated by high-performance hardware or the integer quantization skill [44].

Given the image dataset, the corresponding feature descriptors can be extracted using the aforementioned feature extraction approaches. Based on the different features and distance measures, the affinity matrix can be built, and the corresponding construction times are shown in

Table 11. Affinity matrix construction times of different methods from scratch.

	LIF + L1 in [2]	LIF + L2 in [2]	LIF + Intersection in [2]	UFLF + L1 in [6]	UFLF + L2 in [6]	Ours IRMFRCAMF
Times (s)	4.254	6.801	6.677	4.294	6.789	157.743

. More specifically, the affinity matrix records the affinity between two arbitrary images from the image dataset. If the query image is from the original image dataset, the image retrieval process can be finished by searching the calculated affinity matrix. In this situation, the affinity matrix calculation is an offline process, and the image retrieval task can be completed very quickly. Only if the query image does not come from the image dataset or if the volume of the image dataset changes does the affinity matrix need to be recalculated. Hence, in most cases, the affinity matrix calculation complexity does not directly influence the efficiency of the image retrieval approach.

5.3. Experiments on WH Dataset

Fixing the parameter configuration of the unsupervised feature learning module and the collaborative affinity metric fusion module, the proposed IRMFRCAMF is tested on the WH dataset [33]. As introduced in Section 5.1.1, the WH dataset is composed of 19 land cover categories, and each class contains 50 image scenes. Some sample image scenes from the WH dataset are shown in Figure 11. For conciseness, the airport class, the beach class, the bridge class, the commercial class, the desert class, the farmland class, the football field class, the forest class, the industrial class, the meadow class, the mountain class, the park class, the parking class, the pond class, the port class, the railway station class, the residential class, the river class, and the viaduct class are abbreviated by the 1st–19th classes, respectively.

In this experiment, our proposed IRMFRCAMF is compared with LIF + L1 in [2], LIF + L2 in [2], LIF + Intersection in [2], UFLF + L1 in [6], and UFLF + L2 in [6]. The corresponding quantitative comparison results are reported in Figure 12 and

Table 12. Dataset-level precision (DP) under different methods.

	LIF + L1 in [2]	LIF + L2 in [2]	LIF + Intersection in [2]	UFLF + L1 in [6]	UFLF + L2 in [6]	Ours IRMFRCAMF
DP	0.5795	0.5568	0.5795	0.5853	0.5821	0.7526

. From Figure 12, we can easily see that our IRMFRCAMF can significantly outperform the existing approaches in the majority of categories. In addition, our IRMFRCAMF can outperform the existing approaches as measured by the comprehensive indicator (i.e., the dataset-level precision). As depicted in Table 12, our IRMFRCAMF can achieve nearly a 20% performance improvement compared with the existing approaches. The performance improvement on the WH dataset is approximately equal to that on the UCM dataset.

Figure 13 and Figure 14 provide a visual comparison of the different methods. As depicted in Figure 13, the existing approaches including LIF and UFLF easily confuse the pond class and the river class. In contrast, our IRMFRCAMF can robustly output the right image scenes based on the query. As depicted in Figure 14, the retrieval performance of the existing approaches on the viaduct class is still less than satisfactory. Even in this situation, our IRMFRCAMF still works well.

In the following, we report the running times of the main stages of the presented method and the other methods.

Table 13. Training times of the proposed unsupervised feature learning neural networks.

	UCNN with One Feature Layer	UCNN with Two Feature Layers	UCNN with Three Feature Layers	UCNN with Four Feature Layers
Times (s)	32.802	1648.555	3643.574	3672.956

provides the training times of four unsupervised convolutional neural networks on the WH dataset. Through a training time comparison between Table 9 and Table 13, we can easily see that the training time is basically stable between the two datasets.

Table 14. Feature extraction times of different single features per one image scene.

	LIF in [2]	UFLF in [6]	UCNN1	UCNN2	UCNN3	UCNN4
Code Type	C++	C++	Matlab	Matlab	Matlab	Matlab
Times (s)	0.354	0.364	12.592	142.214	95.538	47.723

reports the feature extraction times. The feature extraction time of an image from the WH dataset as a function of the size of the image scene is much larger than that of the UCM dataset.

The affinity matrix construction times of the different methods are provided in

Table 15. Affinity matrix construction times of different methods from scratch.

	LIF + L1 in [2]	LIF + L2 in [2]	LIF + Intersection in [2]	UFLF + L1 in [6]	UFLF + L2 in [6]	Ours IRMFRCAMF
Time (s)	0.628	0.916	1.038	0.631	0.910	18.851

. The affinity matrix construction on the WH dataset takes a much smaller time as a function of the volume of the dataset than that on the UCM dataset.

6. Conclusions

In order to improve the automatic management of high-resolution remote sensing images, this paper proposes a novel content-based high-resolution remote sensing image retrieval approach via multiple feature representation and collaborative affinity metric fusion (IRMFRCAMF). Derived from unsupervised multilayer feature learning [14], this paper designs four networks that can generate four types of unsupervised features: the aforementioned UCNN1, UCNN2, UCNN3, and UCNN4. The proposed unsupervised features can achieve better image retrieval performance than the traditional feature extraction approaches such as LBP, GLCM, MR8, and SIFT. In order to make the most of the introduced complementary features, this paper advocates collaborative affinity metric fusion to measure the affinity between images. Large numbers of experiments show that the proposed IRMFRCAMF can dramatically outperform two existing approaches, including LIF in [2] and UFLF in [6].

It is well known that feature representation is a fundamental module in various visual tasks. Hence, in addition to high-resolution remote sensing image retrieval, the proposed unsupervised features would probably benefit other tasks in computer vision such as feature matching [45,46], image fusion [47], and target detection [48]. In our future work, the proposed unsupervised features will be evaluated on more tasks. In addition, we will extend the proposed IRMFRCAMF to more applications in the remote sensing community. For example, the proposed IRMFRCAMF will be utilized to generate labeled samples for scene-level remote sensing image interpretation tasks such as land cover classification [14], built-up area detection [49], urban village detection [50], and urban functional zoning recognition [51].