For the synergy of L-band
and freeboard measurements, we adopt two existing physical models that constrain the observational data with the sea ice parameters. The first model is the L-band radiation model [
32], which simulates the L-band (1.4 GHz) brightness temperature of the sea ice cover based on its parameters. The second model is the hydrostatic equilibrium model based on buoyancy relationship, which is widely used in satellite altimetry.
Section 2.1 gives a short introduction to these models, including the parameters as adopted by the retrieval algorithms. Based on these two forward models, the inverse problem of retrieval is studied in
Section 2.2 for the synergy between
and
and that between
and
. The analysis of the properties of the solution space and the potential problem of ill-posedness is the basis of the design of retrieval methods in
Section 3.
2.1. Forward Models
The first physical model as adopted by the retrieval is the L-band (1.4 GHz) radiation model. The original model was developed for modeling the radiative transfer of soil moisture at L-band, as in Burke et al. [
33]. The adapted version of the model was applied for the sea ice that are related to the retrieval with SMOS data [
31]. Specifically, in Kaleschke et al. [
21] introduced the detailed modeling of the dielectric properties of the sea ice, and in Maaß et al. [
31] the model was extended to include a snow layer over the sea ice and further applied for the snow depth retrieval. In Zhou et al. [
32], the model was further improved to include more realistic characterization of the small-scale sea ice variabilities. Due to the sensitivity of the radiative properties to the salinity in the sea ice [
21], the vertical salinity profile is integrated in the multi-layer formulation of the model. Sea ice type dependent salinity profile was adopted to reflect the more thorough salinity drainage and flushing of MYI as compared with FYI. Besides, as discussed in Zhou et al. [
32], the open water or (refrozen) sea ice leads could have profound impact on the overall L-band
, we limit the discussion in this article to the theoretical studies which: (1) only apply to normal Arctic winter conditions, and (2) involve no mixture of open water or sea ice types. In Zhou et al. [
32], the improved multi-layer radiation model was verified with observational data including SMOS and Operation IceBridge (OIB [
34]). There was good agreement between the modeled and the observational
(
as high as 0.81, with a correction factor of about 1.8 K).
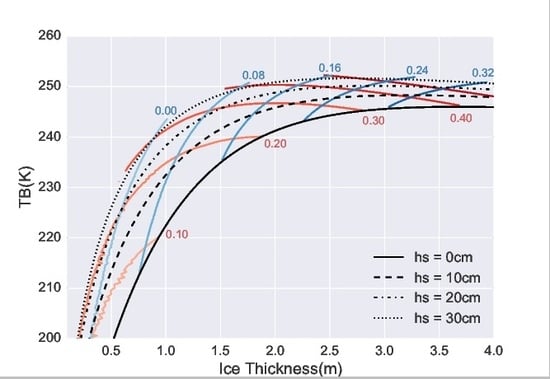
Figure 2 shows the simulated
with respect to sea ice parameters (
and
), under normal Arctic winter conditions (the surface temperature of −30
C). There is non-linear relationship between
and
or
. With the deepening of either the sea ice or the snow cover (i.e., increasing
or
), the value of
gradually saturates for both FYI and MYI. For
larger than about 2.5 m (1.2 m) for MYI (FYI), the value of
saturates. For the retrieval of
based on a prescribed
, this implies that a small perturbation/error in the observed
would result in a large difference in the retrieved
, as in Tian-Kunze et al. [
22]. Also due to the nonlinear relationship, the retrieval cannot be formulated in an explicit form. We use Equation (
1) to represent the nonlinear relationship between
and related parameters, including: surface temperature (
), sea ice type (
), sea water temperature (
) and sea water salinity (
) at the bottom of the sea ice.
The second physical model as adopted by the retrieval is the hydrostatic equilibrium model based on the buoyancy relationship between
,
and the density of sea ice, snow and sea water (
,
and
). This model is the basis of both radar and laser satellite altimetry [
8,
10,
35]. For radar altimetry as in CryoSat-2 [
13,
36,
37], the sea ice thickness can be estimated with
as derived from satellite data, according to Equation (
2). For laser altimetry as in ICESat [
8,
38], the same model is applied with a different form involving
, as shown in Equation (
3).
Since the linear relationship between
and
or
, the retrieval of
can be formulated in the explicit form above. The value of
is treated as a priori knowledge which can be estimated from other sources (see
Section 1).
For the retrieval, we treat
,
and
as input parameters, and
and
the retrieved parameters. Other parameters as used by the models are categorized as model parameters, which are either treated as constants or assumed to be derived from other sources. For the radiation model,
is assumed to be derived from remote sensing or reanalysis data. In this article, we mainly consider the typical winter condition of the Arctic, and the surface temperature is assumed to be −30
C Besides, we also consider the relatively warmer condition (
= −15
C) in the sensitivity studies, which is becoming more common with global warming [
39]. The values of
and
are considered as constants (
= −1.8
C and
= 33 g/kg). Following common practice in satellite altimetry, density values are assumed constant:
= 1024 kg/m
and
= 915 kg/m
, as derived from field measurements [
40], and
= 320 kg/m
following Warren et al. [
25]. Although these model parameters are assumed to be constant, the uncertainty as caused by these parameters are all analyzed systematically for the sensitivity studies in
Section 4.
With the transformed forms of Equations (
2) and (
3), we can also derive
and
based on
and
. In
Figure 2, the colored lines (with labels) represent constant
(blue lines) and constant
(red lines). Since
and
are input parameters, the solution to the retrieval based on
and freeboard synergy resides on the corresponding constant freeboard lines. For the synergy between
and
,
increases monotonically on each constant
line, in spite of the saturation and minor decrease of
with respect to
. This implies good potential of retrieving
and
based on
and
. However, for the synergy between
and
, under certain values of
(e.g., 0.12 m for FYI and 0.30 m for MYI), there is no monotonic increase of
with the increase of
. This implies that for certain combinations of
and
, there may exist more than 1 solution to the retrieval problem. It is worth noting that for thick sea ice, there is potentially better sensitivity for both schemes of synergy, as indicated by the non-flat constant freeboard lines with respect to
.
2.2. Retrievability Analysis
We construct the solution space for the retrieval problems by scanning the sea ice parameters. For each scanned values of and , we generate the values of , and . We exclude the cases involving inundation (i.e., ), which is uncommon for Arctic regions. The solution space for each of the data synergy scheme is plotted and examined with respect to the input parameters.
For the synergy between
and
,
Figure 3a,b show the solution space for
and
respectively for FYI, and
Figure 3c,d show those for MYI. A reasonable range of the solution space for both
and
is included (
within about 10 m and
within 1 m). With a certain value of
, there exists a range of possible
values. For FYI, with the increase in
, the lowest possible value of
also increases. For MYI, there is a slight decrease of the lowest bound of
when
is high. Due to the saturation of
with respect to either
or
, there also exists an upper bound for
. Under certain value of
(or
), the solutions of both
and
become larger with the increase of
(or
).
Figure 4 shows the solution space for the synergy between
and
. As compared with the corresponding information in
Figure 3, there exists evident differences. The most prominent difference from the synergy between
and
is the presence of two potential solutions for certain part of the solution space. Therefore, the retrieval problem of the synergy between
and
is not well-posed. In each subfigure, the portion of the solution space that involves two potential solutions is outlined by dotted lines in the main part. The other solution of this portion of the solution space is also shown by embedded graph in each subfigure. The corresponding input parameters are as follows: (1) for FYI,
around 0.1 m and
around 237 K, (2) for MYI,
around 0.37 m and
around 247 K. For FYI, this portion consists of a small part (3.32%) of the solution space, and the corresponding two solutions for
(
) are about 0.4 m and 0.9 m (0.1 m and 0.07 m). For MYI, the proportion is higher (6.67%), and the two potential solutions for
(
) are about 1.3 m and 2.8 m (0.3 m and 0.12 m).
We also consider the relatively warmer Arctic condition with
= −15
C, instead of the normal winter condition (
= −30
C). Examination of the corresponding solution space is carried out in a similar manner. The results (not shown) indicate that under the relatively warmer condition, the range of
is from 247 K to 255 K (250 K to 257 K) when
is large in FYI (MYI) algorithm. This range is narrower as compared to winter condition (
Figure 3). However, the well-posedness (ill-posedness) of the retrieval problem for the synergy between
and
(
) is not changed. Besides, the portion of the solution space that involves two solutions takes up about
(
) for FYI (MYI).
To summarize, there exists retrievability of sea ice parameters with the observational data of L-band and freeboard measurements. For typical parameters, both and can be attained given the combination of and or . The synergy between and is always well-posed, while for that between and there is potential of two solutions. These characteristics of the solution space should be accounted for by the retrieval algorithms.