Use of High-Quality and Common Commercial Mirrors for Scanning Close-Range Surfaces Using 3D Laser Scanners: A Laboratory Experiment
Abstract
:1. Introduction
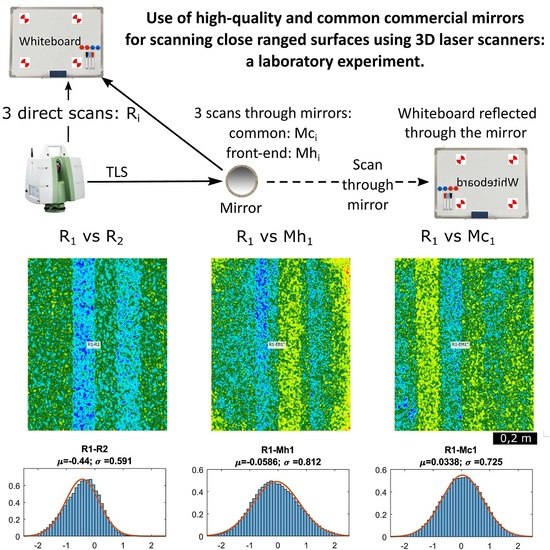
2. Materials and Methods
3. Results
3.1. Comparison of Direct Scans
3.2. Errors Found When Scanning through a High-Quality Mirror
3.3. Errors Found When Scanning through a Common Mirror
4. Discussion
4.1. Indentification of Error Sources
4.2. Errors Due to the Scanning through Mirrors
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Slob, S. Automated Rock Mass Characterisation Using 3-D Terrestrial Laser Scannin; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Shan, J.; Toth, C.K. Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.-H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LiDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef]
- Thiel, K.H.; Wehr, A. Performance capabilities of laser scanners—An overview and measurement principle analysis. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Istanbul, Turkey, 12–23 July 2004; Volume 36, pp. 14–18. [Google Scholar]
- Boehler, W.; Vicent, M.B.; Marbs, A. Investigating laser scanner accuracy. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Dresden, Germany, 8–10 October 2003; Volume 34, pp. 696–701. [Google Scholar]
- Costantino, D.; Angelini, M.G. Qualitative and quantitative evaluation of the luminance of laser scanner radiation for the classification of materials. In Proceedings of the ISPRS-International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Strasbourg, France, 2–6 September 2013; Volume 1, pp. 207–212. [Google Scholar]
- Kukko, A.; Kaasalainen, S.; Litkey, P. Effect of incidence angle on laser scanner intensity and surface data. Appl. Opt. 2008, 47, 986–992. [Google Scholar] [CrossRef] [PubMed]
- Carrea, D.; Abellán, A.; Humair, F.; Matasci, B.; Derron, M.-H.; Jaboyedoff, M. Correction of terrestrial LiDAR intensity channel using Oren–Nayar reflectance model: An application to lithological differentiation. ISPRS J. Photogramm. Remote Sens. 2016, 113, 17–29. [Google Scholar] [CrossRef]
- Wunderlich, T.; Wasmeier, P.; Ohlmann-Lauber, J.; Schäfer, T.; Reidl, F. Objective Specifications of Terrestrial Laserscanners—A Contribution of the Geodetic Laboratory at the Technische Universität München; Lehrstuhl für Geodäsie, TUM: München, Germany, 2013; ISBN 978-3-943683-21-9. [Google Scholar]
- Baltsavias, E. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Wehr, A.; Lohr, U. Airborne laser scanning—An introduction and overview. ISPRS J. Photogramm. Remote Sens. 1999, 54, 68–82. [Google Scholar] [CrossRef]
- Pu, S.; Rutzinger, M.; Vosselman, G.; Oude Elberink, S. Recognizing basic structures from mobile laser scanning data for road inventory studies. ISPRS J. Photogramm. Remote Sens. 2011, 66, S28–S39. [Google Scholar] [CrossRef]
- Liang, X.; Kukko, A.; Kaartinen, H.; Hyyppä, J.; Yu, X.; Jaakkola, A.; Wang, Y. Possibilities of a Personal Laser Scanning System for Forest Mapping and Ecosystem Services. Sensors 2014, 14, 1228–1248. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial laser scanning in forest inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform Mobile Laser Scanning: Usability and Performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef]
- Alho, P.; Kukko, A.; Hyyppä, H.; Kaartinen, H.; Hyyppä, J.; Jaakkola, A. Application of boat-based laser scanning for river survey. Earth Surf. Process. Landf. 2009, 34, 1831–1838. [Google Scholar] [CrossRef]
- Abellán, A.; Derron, M.-H.; Jaboyedoff, M. ‘Use of 3D Point Clouds in Geohazards’ Special Issue: Current Challenges and Future Trends. Remote Sens. 2016, 8, 130. [Google Scholar] [CrossRef]
- McKinion, J.M.; Willers, J.L.; Jenkins, J.N. Comparing high density LIDAR and medium resolution GPS generated elevation data for predicting yield stability. Comput. Electron. Agric. 2010, 74, 244–249. [Google Scholar] [CrossRef]
- Johnson, K.M.; Ouimet, W.B. Rediscovering the lost archaeological landscape of southern New England using airborne light detection and ranging (LiDAR). J. Archaeol. Sci. 2014, 43, 9–20. [Google Scholar] [CrossRef]
- Levinson, J.; Askeland, J.; Becker, J.; Dolson, J.; Held, D.; Kammel, S.; Kolter, J.Z.; Langer, D.; Pink, O.; Pratt, V.; et al. Towards fully autonomous driving: Systems and algorithms. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden-Baden, Germany, 5–9 June 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 163–168. [Google Scholar]
- Amzajerdian, F.; Pierrottet, D.; Petway, L.; Hines, G.; Roback, V. Lidar systems for precision navigation and safe landing on planetary bodies. In Proceedings of the 2011-International Symposium on Photoelectronic Detection and Imaging, Beijing, China, 24–26 May 2011; Volume 8192, p. 819202. [Google Scholar]
- Matasci, B.; Carrea, D.; Abellán, A.; Derron, M.H.; Humair, F.; Jaboyedoff, M.; Metzger, R. Geological mapping and fold modeling using terrestrial laser scanning point clouds: Application to the Dents-du-Midi limestone massif (Switzerland). Eur. J. Remote Sens. 2015, 48, 569–591. [Google Scholar] [CrossRef]
- Lato, M.J.; Diederichs, M.S. Mapping shotcrete thickness using LiDAR and photogrammetry data: Correcting for over-calculation due to rockmass convergence. Tunn. Undergr. Space Technol. 2014, 41, 234–240. [Google Scholar] [CrossRef]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial laser scanning of rock slope instabilities. Earth Surf. Process. Landf. 2014, 39, 80–97. [Google Scholar] [CrossRef]
- Yang, S.-W.; Wang, C.-C. On Solving Mirror Reflection in LIDAR Sensing. IEEE/ASME Trans. Mechatron. 2011, 16, 255–265. [Google Scholar] [CrossRef]
- Fasano, A.; Callieri, M.; Cignoni, P.; Scopigno, R. Exploiting mirrors for laser stripe 3D scanning. In Proceedings of the International Conference on 3-D Digital Imaging and Modeling, 3DIM, Banff, AB, Canada, 6–10 October 2003; IEEE: Piscataway, NJ, USA, 2003; pp. 243–250. [Google Scholar]
- Leica Geosystems AG. Leica ScanStation C10 Data Sheet; Leica Geosystems AG: Heerbrugg, Switzerland, 2011. [Google Scholar]
- Reshetouski, I.; Ihrke, I. Mirrors in computer graphics, computer vision and time-of-flight imaging. In Time-of-Flight and Depth Imaging. Sensors, Algorithms, and Applications; Springer: Berlin, Germany, 2013; pp. 77–104. [Google Scholar]
- Leica Cyclone v9.1 2016. Available online: http://hds.leica-geosystems.com/en/Support-Downloads-Cyclone-Downloads_27054.htm (accessed on 9 November 2017).
- Lague, D.; Brodu, N.; Leroux, J.J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (NZ). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]










| Compared to | R1 | R2 | R3 |
|---|---|---|---|
| Mh1′′ | −0.06/0.81 | 0.36/0.76 | 0.25/0.67 |
| Mh2′′ | −0.2/0.8 | 0.23/0.67 | 0.11/0.79 |
| Mh3′′ | −0.16/0.74 | 0.26/0.68 | 0.11/0.62 |
| Mc1′′ | 0.03/0.72 | 0.46/0.68 | 0.35/0.5 |
| Mc2′′ | 0.02/0.65 | 0.44/0.63 | 0.32/0.68 |
| Mc3′′ | −0.24/0.72 | 0.18/0.69 | 0.06/0.53 |
| R1 | - | −0.44/0.59 | −0.31/0.58 |
| R2 | −0.44/0.59 | - | 0.12/0.56 |
| R3 | −0.31/0.58 | 0.12/0.56 | - |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riquelme, A.J.; Ferrer, B.; Mas, D. Use of High-Quality and Common Commercial Mirrors for Scanning Close-Range Surfaces Using 3D Laser Scanners: A Laboratory Experiment. Remote Sens. 2017, 9, 1152. https://doi.org/10.3390/rs9111152
Riquelme AJ, Ferrer B, Mas D. Use of High-Quality and Common Commercial Mirrors for Scanning Close-Range Surfaces Using 3D Laser Scanners: A Laboratory Experiment. Remote Sensing. 2017; 9(11):1152. https://doi.org/10.3390/rs9111152
Chicago/Turabian StyleRiquelme, Adrián J., Belén Ferrer, and David Mas. 2017. "Use of High-Quality and Common Commercial Mirrors for Scanning Close-Range Surfaces Using 3D Laser Scanners: A Laboratory Experiment" Remote Sensing 9, no. 11: 1152. https://doi.org/10.3390/rs9111152
APA StyleRiquelme, A. J., Ferrer, B., & Mas, D. (2017). Use of High-Quality and Common Commercial Mirrors for Scanning Close-Range Surfaces Using 3D Laser Scanners: A Laboratory Experiment. Remote Sensing, 9(11), 1152. https://doi.org/10.3390/rs9111152