Comparison of Spatial Interpolation and Regression Analysis Models for an Estimation of Monthly Near Surface Air Temperature in China

Abstract

Near surface air temperature (NSAT) is a primary descriptor of terrestrial environmental conditions. In recent decades, many efforts have been made to develop various methods for obtaining spatially continuous NSAT from gauge or station observations. This study compared three spatial interpolation (i.e., Kriging, Spline, and Inversion Distance Weighting (IDW)) and two regression analysis (i.e., Multiple Linear Regression (MLR) and Geographically Weighted Regression (GWR)) models for predicting monthly minimum, mean, and maximum NSAT in China, a domain with a large area, complex topography, and highly variable station density. This was conducted for a period of 12 months of 2010. The accuracy of the GWR model is better than the MLR model with an improvement of about 3 °C in the Root Mean Squared Error (RMSE), which indicates that the GWR model is more suitable for predicting monthly NSAT than the MLR model over a large scale. For three spatial interpolation models, the RMSEs of the predicted monthly NSAT are greater in the warmer months, and the mean RMSEs of the predicted monthly mean NSAT for 12 months in 2010 are 1.56 °C for the Kriging model, 1.74 °C for the IDW model, and 2.39 °C for the Spline model, respectively. The GWR model is better than the Kriging model in the warmer months, while the Kriging model is superior to the GWR model in the colder months. The total precision of the GWR model is slightly higher than the Kriging model. The assessment result indicated that the higher standard deviation and the lower mean of NSAT from sample data would be associated with a better performance of predicting monthly NSAT using spatial interpolation models.

1. Introduction

Near surface air temperature (NSAT) is a key factor in energy and water exchanges between the land surface and atmosphere [1]. NSAT is the most important component of global climate change and is sensitive to local anthropogenic disturbance [2]. Thus, the availability of NSAT with a high spatial resolution is deemed necessary for several applications such as hydrology, meteorology, and ecology [3,4,5]. Near surface air temperature is commonly measured at a standard meteorological shelter height (2.0 m height above the ground) through meteorology observing stations with a high accuracy and temporal resolution [6,7]. For decades, many efforts have been made to obtain spatial distributions of various NSAT variables based on the point station measurements, including annual maximum/minimum/mean NSAT [8], monthly maximum/minimum/mean NSAT [9,10,11,12,13], daily maximum/minimum/mean NSAT [14,15,16,17,18,19], and instantaneous NSAT [20,21]. These NSAT retrieval methods can be divided into three groups: (1) spatial interpolation method [22], (2) physical-based method [20,23], and (3) regression analysis method [8].

Considering the high spatial autocorrelation of NSAT, several spatial interpolation methods have been employed to generate spatially continuous NSAT from point station measurements, including inverse distance weighting (IDW), Spline, Kriging, and even more sophisticated methods, such as co-Kriging and elevation-de-trended Kriging techniques [24,25,26]. The performance of interpolation methods is highly dependent on the spatial density and distribution of weather stations [27]. Satellite remote sensing provides the ability to extract spatially continuous information of land surface characteristics such as land surface temperature (LST) and the vegetation index (VI), which are closely relative to NSAT. Sun et al. proposed a physically-based model for NSAT estimations from satellite data based on thermodynamics, which requires LST, net radiation, aerodynamic resistance, and crop water stress as the input [20]. The physically-based model was performed to retrieve instantaneous NSAT from MODIS data for the North China Plain, and the result showed an accuracy which was better than 3 °C for 80% of the experimental data [20]. Stisen et al. presented a semi-empirical model of the temperature vegetation index (TVX) under the assumption that NSAT is more close to LST with increasing of the Normalized Difference Vegetation Index (NDVI) for land surface, and NSAT was assumed to be equal to LST corresponding to the effective full vegetation cover [28]. Nieto et al. introduced the improved maximum NDVI estimation in TVX method to retrieve NSAT from MSG-SEVIR data for the Iberian Peninsula in 2005, and they achieved an accuracy of between 3 °C and 5 °C [29].

The regression analysis methods for estimating NSAT take advantage of the correlations between NSAT and other environmental variables. Kawashima et al. [30], Cheng et al. [31], Fu et al. [6], and Zhu et al. [3] tried to predict NSAT based on the simple correlation between the NSAT and LST. Multiple linear regression (MLR) analysis using both remote sensing and geographical variables, including LST, VI, latitude, altitude, and so on, as predictors was performed to model NSAT [7,8,9,18]. However, a global regression analysis may miss local details that can be significant if the relationship is spatially non-stationary. Geographically weighted regression (GWR) is a local modelling technique for analyzing spatial analysis, and allows the regression model parameters to vary in space [32,33]. The GWR model was employed by Chen et al. for estimating monthly and eight-days NSAT in China [12].

Many researches have made contributions to assess the performance of various predicting NSAT models in different regions. Peng et al. interpolated the monthly and annual NSAT in the Jiangsu province, China, using the IDW, Spline, Kriging, and Co-Kriging models, and the result proved that the Kriging model has a much higher precision than the IDW and Spline models, and that the Co-Kriging model is slightly better than the Kriging model [34]. GLASS et al.’s study showed that interpolation models (i.e., the Kriging model), regardless of whether or not satellite data are included, are consistently superior to MLR models, and the Kriging model without satellite data performed similarly to that with satellite data under more general conditions [22]. Zhao et al. estimated the NSAT in the southern Qilian mountains, China, in which the weather stations are sparse, and the result indicated that the accuracy of the MLR model is higher than that of spatial interpolation models, and the Spline model shows the worst result [35]. Most of the studies are performed by comparative analysis in a relatively small region at one or a few time points. In addition, less work has been conducted comparing the GWR model with other methods.

The interpolation models are based on the autocorrelation of NSAT, while the regression analysis models are based on the correlation of NSAT with other factors. Two kinds of models exhibit a different performance of predicting NSAT under varied climatic, geographical, and environmental conditions. The objective of this study is to evaluate the performance of three spatial interpolation (i.e., IDW, Spline, and Kriging) and two regression analysis (i.e., MLR and GWR) methods for predicting monthly NSAT considering the large region, significant seasonal differences, and the variable weather station density. China continent was selected as the study area, and 12 months of 2010 was considered as the study period. This paper is organized as follows: Section 2 describes the study area and materials. Section 3 presents the methods for predicting NSAT, including three spatial interpolation and two regression analysis models. Section 4 gives the assessment results of predicting monthly NSAT using various methods. Finally, the study is discussed and concluded in Section 5 and Section 6.

2. Study Area and Materials

2.1. Study Area

China is located in the east and middle of Asia and on the west shore of the Pacific Ocean, with a land area of approximately 9.6 million km², across 50 degrees of latitude (see Figure 1). The terrain of China is high in the west but low in the east, showing a ladder-like distribution. Mountains, plateaus, and hills cover about 67% of the land area, while basins and plains cover about 33%. Because of the wide range of latitudes and complex topography, China has a varied climate. Based on temperature zones, China can be divided into tropical, subtropical, warm temperate, moderate temperate, cold temperate, and Tibetan Plateau zones.

China has a marked continental monsoonal climate characterized by great variety. In January, there is a 0 °C isotherm through the Qinling Mountains to the Huaihe River and then the southeast boundary of the Tibetan plateau. NSAT north of the line is below 0 °C and is lower than −30 °C in Mohe County, Helongjiang province, while NSAT south of the line is above 0 °C, and is higher than 20 °C in Hainan province. There is a big NSAT difference between the north and south of China in winter. In July, NSAT in most regions of China is greater than 20 °C, except for the high terrain regions, such as the Tibetan Plateau and Tianshan Mountains. In summer, high temperatures are prevalent, with a small NSAT difference between the north and south of China.

2.2. Satellite Data

The MODIS VI products (MOD13) provide consistent spatial and temporal time series comparisons of global vegetation conditions, including standard NDVI and Enhance Vegetation Index values. MODIS VIs are calculated using the VI algorithm equations from MODIS land surface reflectances corrected for molecular scattering, ozone absorption, and aerosols. In this study, NDVI was employed to predict the monthly NSAT. The MOD13A3 is the monthly VI product at a 1 km spatial resolution produced by averaging one month of daily VI product.

The MODIS LST products are generated using the generalized split-window LST algorithm from MODIS bands 31 and 32 (MOD11_L2) [36,37] and using the day/night LST algorithm from pairs of daytime and nighttime observations in seven MODIS TIR bands (MOD11B1) [38]. MOD11A2 is a tile of the eight-day LST product at a resolution of 1 km produced by averaging eight days of the daily LST product. In this study, the daytime LST from MOD11A2 data was employed to predict monthly NSAT.

The MOD13A3 and MOD11A2 products covering China territory in 2010 were collected [39]. The MODIS products were preprocessed, including projection, mosaicking, and clipping, using MRT software. In addition, monthly LST data were generated by averaging four MOD11A2 data sets for each calendar month of 2010.

2.3. Station Data

Daily NSAT (i.e., minimum, maximum, and mean NSAT) data in 2010 were provided by the China Meteorological Data Service Center [40]. These data were collected from 2132 meteorological stations in China. As shown in Figure 1, the stations are not uniformly distributed over the entire country and the station density decreases from the southeast to the northwest. These stations were roughly divided into two groups based on the green line in Figure 1. The densities of northwest and southeast groups are about 0.41 and 4.16 per ten thousand km², respectively. To predict monthly NSAT, the daily NSAT were aggregated to monthly NSAT. The station data are organized based on geographical areas, i.e., the spatially adjacent weather stations were listed together. In this study, the stations were selected as validation stations at five station intervals from a station list and the remaining stations were considered as prediction stations (see Figure 1). Separating the prediction and evaluation sets in this way is conducted to ensure that the stations for prediction and evaluation are scattered over the whole study area.

2.4. Elevation Data

The global digital elevation model (DEM) at the spatial resolution of 90 m that was produced by the NASA Shuttle Radar Topographic Mission (SRTM) was collected [41]. In this study, the SRTM DEM data were resampled from 90 m to 1 km to render them consistent with the MODIS product (see Figure 1).

3. Methods

3.1. Spatial Interpolation Models

Three interpolation models integrated in ArcGIS software were employed to predict monthly NSAT, including Kriging, IDW, and Spline models. The IDW interpolation method estimates point values by averaging the values of nearby sample data points with distance-based functions as weight. The Spline estimates values using a mathematical function that minimizes overall surface curvature, resulting in a smooth surface that passes exactly through the input points. The Kriging is an advanced geostatistical procedure that generates an estimated surface from a scattered set of points with z-values. The detail of these three interpolation models can be found in ArcGIS Desktop Help [42].

In order to employ the spatial interpolation model, many configuration parameters need to be set. For the IDW model, the power which is used to control the significance of the surrounding points on the interpolated value was set to 2. For the Kriging model, the ordinary Kriging method and the spherical semivariogram model were selected. As for the Spline model, the regularized type was employed. The number of points was set to 30 for all the three spatial interpolation models. The search radius for the IDW and Kriging models was set as ‘Variable’.

3.2. Standard Multiple Linear Regression Model

Cristóbal et al. [8] presented a method for predicting NSAT using standard MLR by means of remotely sensed and geographic variables, which can be expressed as:

$$Y={\beta }_0+{\displaystyle \sum _{i=1}^p{\beta }_i}{X}_i+\epsilon$$

(1)

where Y represents the dependent variable (i.e., NSAT); X_i represents the explanatory variable; ${\beta }_0$ and ${\beta }_i$ are the intercept and the slope of the relationship between the dependent and explanatory variables, respectively; and $\epsilon$ is the regression residual. To perform MLR analysis, geographic and remotely sensed variables are considered as explanatory variables. The geographic variable includes altitude and latitude, and the remotely sensed variable includes LST and NDVI. According to the coordinates of the weather station, the LST and NDVI values for the weather station were extracted from the LST and NDVI data, respectively.

The basic assumption of this method is that altitude, latitude, LST, and NDVI have a significant correlation with NSAT. However, the values of altitude and NDVI are usually constant over regions covered by snow and lakes, which contradicts this assumption, so the pixels of water body and snow are removed from further analysis. The MOD10CM snow cover product was used to mask snow cover.

3.3. Geographically Weighted Regression Model

The standard MLR model is based implicitly upon the assumption of spatial stationarity in the relationship between the dependent variable Y and explanatory variables X_i (i = 1, 2, … p), and the estimated parameters are assumed to be constant over space. In contrast, the GWR is a regional regression method that can be used to investigate the non-stationary relationship between the dependent and explanatory variables. The GWR expands the MLR method for use with spatial data. With geographically weighted regression, the relationship between the dependent variable Y and explanatory variables X_i can be expressed as:

$$Y_j={\beta }_0\left(u_j,v_j\right)+{\displaystyle \sum _{i=1}^p{\beta }_i\left(u_j,v_j\right)}{X}_{ij}+{\epsilon }_j$$

(2)

where ${\beta }_0\left(u_j,v_j\right)$ and ${\beta }_i\left(u_j,v_j\right)$ are the intercept and the slope estimated at the jth point, respectively; ${\epsilon }_j$ is the regression residual at the jth point; and $\left(u_j,v_j\right)$ are the coordinates of the jth point. Unlike a global regression method, the coefficients in Equation (2) are estimated by the observations around the jth point, and the contribution of an observation site to the coefficients estimate for the jth point is weighted using a distance decay function based on the assumption that the observations near to the jth point would have more influence on the estimate than those further away. Therefore, the coefficients can be obtained from:

$$\widehat{\beta }\left(u_j,v_j\right)={\left(X^T\left(W\left(u_j,v_j\right)\right)X\right)}^{-1}{X}^{T}W\left(u_j,v_j\right)Y$$

(3)

where $\widehat{\beta }\left(u_j,v_j\right)$ represents the local coefficients to be estimated at location $\left(u_j,v_j\right)$; X and Y are the vectors of the explanatory and the dependent variables, respectively; and $W\left(u_j,v_j\right)$ is the weight matrix. Gaussian and bi-square kernel functions are two common kernel types for the GWR model. The Gaussian kernel weights gradually decrease from the center of the kernel, but never reach zero. The bi-square kernel function has a clear-cut range where the weighting is non-zero [12]. In this study, the adaptive bi-square function is used to derive the weight matrix:

$$\begin{array}{l}{w}_{ij}={\left[1-{\left(d_{ij}/b\right)}^2\right]}^2\mathrm{when}{d}_{ij}\le b\\ \\ w_{ij}=0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{when} d_{ij}>b\end{array}$$

(4)

where $d_{ij}$ is the Euclidean distance between the jth point and neighboring observation i and $b$ is the kernel bandwidth. Golden section search is used to determine the optimal bandwidth. Because the GWR is a regional model, the effect of latitude on NSAT can be assumed to be constant and is excluded in the GWR model. So, only altitude, LST, and NDVI are employed in the GWR model.

3.4. Validation

Ground observations from 20% of weather stations (as mentioned in Section 2.3) are used to assess the performance of the predicted monthly NSAT. Two metrics, including the Root Mean Squared Error (RMSE) and coefficients of determination (R²), are calculated by Equations (5) and (6), respectively:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \sum _{k=1}^n{\left(Y_k-O_k\right)}^2/n}}$$

(5)

$${\mathrm{R}}^2=\frac{\left\{{\displaystyle \sum _{k=1}^n\left[\left(Y_k-\overline{Y}\right)\left(O_k-\overline{O}\right)\right]}\right\}}{{\displaystyle \sum _{k=1}^n\left[{\left(Y_k-\overline{Y}\right)}^2\right]{\displaystyle \sum _{k=1}^n\left[{\left(O_k-\overline{O}\right)}^2\right]}}}$$

(6)

where n represents the number of validation data, Y_k represents the in-situ NSAT in validation site k, O_k represents the predicted NSAT in validation site k, $\overline{Y}$ represents the mean value of in-situ NAST for all validation sites, and $\overline{O}$ represents the mean value of the predicted NSAT for all validation sites.

4. Results

4.1. Comparison between Multiple Linear Regression and Geographically Weighted Regression Models

Figure 2 compares the RMSE and R² of the predicted monthly NSAT using the MLR and GWR models in China in 12 months of 2010. As shown in Figure 2, the RMSEs for the GWR model are less than 2 °C, and the mean RMSEs for 12 months are 1.62 °C for monthly minimum NSAT, 1.52 °C for monthly mean NSAT, and 1.62 °C for monthly maximum NSAT, respectively. The RMSEs for the MLR model are between 2.4 °C and 10.2 °C, and the mean RMSEs for 12 months are 5.6 °C for monthly minimum NSAT, 5.0 °C for monthly mean NSAT, and 4.92 °C for monthly maximum NSAT, respectively. The RMSEs of the predicted monthly minimum, mean, and maximum NSAT using the GWR model are similar. As for the MLR model, the RMSEs decrease in the order from monthly minimum to mean then maximum NSAT. The R² values for the GWR model are between 0.72 and 0.99, and the mean R² values for 12 months are 0.94 for monthly minimum NSAT, 0.92 for monthly mean NSAT, and 0.88 for monthly maximum NSAT, respectively. The R² values for the MLR model are between 0.13 and 0.86, and the mean R² values for 12 months are 0.51 for monthly minimum NSAT, 0.51 for monthly mean NSAT, and 0.45 for monthly maximum NSAT, respectively. The GWR model has much lower RMSE and higher R² values than the MLR model for predicting monthly minimum, mean, and maximum NSAT in all months, which indicates the superiority of the GWR model for predicting monthly NSAT at a large scale compared to the MLR model.

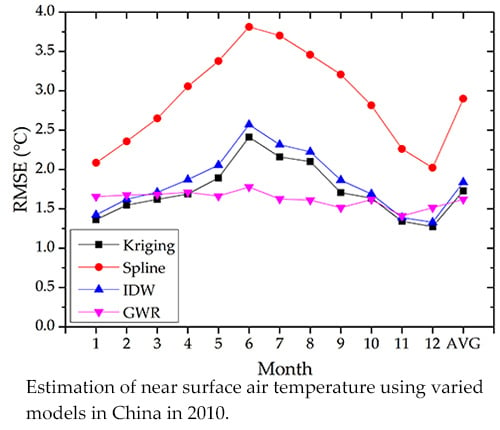
4.2. Comparison between Geographically Weighted Regression and Various Interpolation Models

Figure 3 represents the results of the predicted NSAT using the Kriging and GWR models in June, 2010. The NSAT map derived using the GWR model has more spatial detail than that of the Kriging model. More so, the NSAT map derived using the GWR model includes some ‘Nodata’ due to the missing data (e.g., snow cover and water body), while The NSAT map of the Kriging model includes some ‘Nodata’ which are beyond the spatial scope of the sample data. Figure 4 represents the RMSE and R² of the predicted monthly mean NSAT using the GWR model and three spatial interpolation models in China in 12 months of 2010. As shown in Figure 4, among the three interpolation methods, the RMSEs increase and the R² values decrease in an order from the Kriging model, to the IDW model, to the Spline model, indicating that the Kriging model has the best performance of predicating NAST, followed by the IDW model, and then the Spline model. The RMSEs for three interpolation models increase first and then decrease as the month continues; the R² shows an opposite trend. The RMSEs for the GWR model are stable as the month changes. The R² for the GWR model shows a similar trend as the interpolation methods, but the R² change range for the GWR model is smaller than the three interpolation methods. The RMSEs for the GWR model are higher than those of the Kriging model from January to March and from October to December (indicating the colder months); while they are lower than those of the Kriging model from April to September (indicating the warmer months). During June, July, and August, the RMSE for the GWR model is around 0.5 °C less than that of the Kriging model. The mean RMSEs for 12 months are 1.52 °C for the GWR model, 1.56 °C for the Kriging model, 1.74 °C for the IDW model, and 2.39 °C for the Spline model, respectively. The mean R² values for 12 months are 0.92 for the GWR model, 0.90 for the Kriging model, 0.88 for the IDW model, and 0.80 for the Spline model, respectively.

4.3. Comparison between Different Near Surface Air Temperature Variables

Figure 5 represents the RMSE and R² of the predicted monthly minimum, mean, and maximum NSAT using the GWR model in China in 12 months of 2010. In the colder months (i.e., from January to March and from October to December), the RMESs of the predicted monthly mean NSAT using the GWR model are lower than those of the monthly maximum NSAT, and the RMSEs of the predicted monthly maximum NSAT are lower than those of the predicted monthly minimum NSAT. In the warmer months (i.e., from April to September), the RMSEs of the predicted monthly mean and minimum NSAT are similar, and both of them are lower than those of the predicted monthly maximum NSAT. The mean RMSEs for 12 months using the GWR model are 1.52 °C for monthly mean NSAT, 1.62 °C for monthly minimum NSAT, and 1.62 °C for monthly maximum NSAT, respectively. The R² for monthly minimum, mean, and maximum NSAT are similar in the colder months. The R² decrease in the order from monthly minimum, to mean, to maximum NSAT in the warmer months. Figure 6 represents the RMSE and R² of the predicted monthly minimum, mean, and maximum NSAT using the Kriging model in China in 12 months of 2010. The RMSEs for the Kriging model decrease in an order from monthly maximum, to mean, to minimum NSAT in the warmer months. The mean RMSEs for 12 months using the Kriging model are 1.54 °C for monthly minimum NSAT, 1.57 °C for monthly mean NSAT, and 1.72 °C for monthly maximum NSAT, respectively. The R² for the Kriging model shows a similar trend to the GWR model, but the values are lower than those of the GWR model.

4.4. Comparison between Varied Weather Station Densities

Figure 7 represents the RMSE and R² of the predicted monthly mean NSAT using the GWR and Kriging models in China in 12 months of 2010 considering weather station density. As shown in Figure 7, the RMSE in the region with a high station density is lower than that in the region with a low station density for both GWR and Kriging models in all months. In the region with a high station density, the RMSEs for the GWR and Kriging models are similar in the colder months, while the RMSEs for the GWR model are lower than those of the Kriging model in the warmer months. The mean RMSEs for 12 months are 1.19 °C for the GWR model and 1.29 °C for the Kriging model, respectively. For the region with a low station density, the RMSEs for the GWR model are higher than those of the Kriging model in the colder months, whereas the RMSEs for the GWR model are lower than those of the Kriging model in the warmer model. The mean RMSEs for 12 months are 3.13 °C for the GWR model and 2.92 °C for the Kriging model, respectively. The R² values for all cases decrease firstly and then increase as the month continues. The mean R² values for 12 months are 0.92 for the GWR model in the region of high station density, 0.89 for the Kriging model in the region of high station density, 0.73 for the GWR model in the region of low station density, and 0.75 for the Kriging model in the region of low station density, respectively. The accuracy difference of the predicted monthly NSAT between the regions with the high (i.e., 4.16 per ten thousand km²) and low (i.e., 0.41 per ten thousand km²) station densities can reach 2 °C.

4.5. Comparison between Different Terrain Types

Figure 8 represents the RMSE and R² of the predicted monthly mean NSAT using GWR and Kriging models for varied terrain types in China in 12 months of 2010. As shown in Figure 8b, the RMSEs using the Kriging model for the plateau and plains increase first and then decrease as the month continues. The RMSEs using the Kriging model for hills show little change, while the RMSEs for basins are variable, with month change. The mean RMSEs of 12 months using the Kriging model are 1.99 °C for plateaus, 1.40 °C for basins, 1.18 °C for plains, and 1.01 °C for hills, respectively. As shown in Figure 8c, with month change, the RMSEs using the GWR model for plateaus, hills, and plains are stable, while the RMSEs for basins are variable. The mean RMSEs of 12 months using the GWR model are 2.09 °C for plateaus, 1.41 °C for basins, 0.48 °C for plains, and 1.13 °C for hills, respectively. The mean RMSE for plateaus and basins is higher than that of hills and plains. One possible reason for this is that the weather station density of hills and plains is greater than that of plateaus and basins (please compare Figure 1 and Figure 8a). The mean RMSE of the GWR model is similar to that of the Kriging model for plateaus, basins, and hills. The mean RMSE of the GWR model is significantly lower than that of the Kriging model for plains. Figure 8d,e show that the R² values of both GWR and Kriging models decrease first and then increase as the month progresses for all terrain types. The mean R² values of 12 months using the Kriging model are 0.85 for plateaus, 0.91 for basins, 0.81 for plains, and 0.95 for hills, respectively. The mean R² values of 12 months using the GWR model are 0.85 for plateaus, 0.87 for basins, 0.94 for plains, and 0.94 for hills, respectively.

5. Discussion

Both MLR and GWR models are based on regression analysis, in which the relationship between NSAT and correlative variables was modeled and employed to predict the NSAT. The assessment result of predicting monthly NSAT in China in 2010 shows that the accuracy of the GWR model is better than the MLR model with an improvement of 3 °C in RMSE. Many studies reported that the MLR model achieved an accuracy of below 2 °C for estimating NSAT from a single scene remotely sensed image [8,9]. In the extent of a single scene image, the relationship between NSAT, and LST, VI, latitude, and elevation can be assumed to be stable. However, at a large scale, these relationships are inconsistent in space due to differences in terrain and climate characteristics. The GWR is a local regression model, in which a certain number of observing points around the point to be calculated were employed to fit the model, and the distance between the observing point and the point to be calculated was used as the weight. It can be concluded that the GWR model is more suitable for predicting the NSAT than the MLR model in a large region.

The interpolation methods (i.e., Kriging, Spline, and IDW) for predicting NSAT are based on the spatial autocorrelation of NSAT. The RMSEs for three interpolation models increase first and then decrease as the month progresses (see Figure 4). In addition, the RMSEs for monthly maximum NSAT are larger than those of monthly mean NSAT, and the RMSEs for monthly mean NSAT are larger than those of monthly minimum NSAT from April to September (see Figure 6). The possible reason for this is that the standard deviation (SD) and the mean of NSAT of sample points have an impact on the performance of predicting NSAT using the interpolation methods. As shown in Figure 9, as the month progresses, the SD values of monthly NSAT of 2132 weather stations decrease first and then increase, and the mean values of monthly NSAT of 2132 weather stations increase first and then decrease. The SD values of monthly NSAT decrease and the mean values of monthly NSAT increase in the order from monthly minimum, to mean, to maximum NSAT. Therefore, it may be concluded that the higher SD and the lower mean of NSAT of sample points are associated with the better performance of predicting monthly NSAT using interpolation methods. Compared to interpolation methods, the GWR model is insensitive to the SD and mean of NSAT from sample points (see Figure 5).

In order to perform regression analysis models, the daily LST and NDVI data were aggregated to monthly LST and NDVI data by averaging them. The monthly LST and NDVI have a higher correlation with monthly mean NSAT than that with monthly minimum and maximum NSAT. The regression analysis model for predicting NSAT is based on the correlations between NSAT and related variables. Thus, the higher correlations between NSAT and related variables can contribute to a better performance of predicting NSAT. As shown in Figure 5, the accuracy of the predicted monthly mean NSAT using the GWR model is better than that of monthly minimum and maximum NSAT. As for the Kriging model, the predicting monthly minimum NSAT is better than that of monthly mean and maximum NSAT because the monthly minimum NSAT has the biggest SD and the smallest mean of NSAT from sample data.

The interpolation models only need NSAT data as the input and do not depend on the external assisted data, while the regression analysis models require NSAT data and the related data as the input. The interpolation model is easier to perform and more practical compared with the regression analysis model. The parameter configuration of the spatial interpolation and regression analysis models has a great influence on the accuracy of predicted NSAT, for example, the Kriging type, Spline type, and kernel types for the GWR model, and so on. Investigating the optimized parameter configurations for the interpolation models can make a contribution to improve the precision. Some scholars attempted to perform the composition model for improving NSAT retrieval. Zheng et al. proposed a hybrid methodology by combining the MLR model with spatial interpolation models, proving that the hybrid model is better than MLR model [43]. Chen et al.’s study combined the GWR model with the Kriging model, and showed that the residuals derived using the GWR model are spatially independent, and it is unnecessary to adjust them using the Kriging model [12]. This study only focused on employing the original models and analyzed their characteristics, and so more investigations are needed to develop the comprehensive model taking full advantage of NSAT autocorrelation and correlation with other factors for improving NSAT retrieval.

6. Conclusions

In this study, we investigated and evaluated the performance and robustness of two regression analysis and three spatial interpolation methods for predicting monthly NSAT in China in 2010. Based on the assessment results, some conclusions can be drawn: (1) the GWR model is more suitable for predicting monthly NSAT than the MLR model at a large scale; (2) among the three interpolation methods, the Kriging one has the best performance, followed by IDW, and the Spline shows the poorest results; (3) the GWR model is better than the Kriging model in warmer months, while the Kriging model is superior to the GWR model in colder months; (4) the GWR model is obviously better than the Kriging model for the plains area; and (5) the higher SD and the lower mean of NSAT from sample data would be associated with a better performance of predicting monthly NSAT using interpolation methods. These conclusions are useful to choose the optimal model for predicting NSAT according to different environmental conditions.