Time Series Analysis of Very Slow Landslides in the Three Gorges Region through Small Baseline SAR Offset Tracking

Abstract

Sub-pixel offset tracking has been used in various applications, including measurements of glacier movement, earthquakes, landslides, etc., as a complementary method to time series InSAR. In this work, we explore the use of a small baseline subset (SBAS) Offset Tracking approach to monitor very slow landslides with centimetre-level annual displacement rate, and in challenging areas characterized by high humidity, dense vegetation cover, and steep slopes. This approach, herein referred to as SBAS Offset Tracking, is used to minimize temporal and spatial de-correlation in offset pairs, in order to achieve high density of reliable measurements. This approach is applied to a case study of the Tanjiahe landslide in the Three Gorges Region. Using the TerraSAR-X Staring Spotlight (TSX-ST) data, with sufficient density of observations, we estimate the precision of the SBAS offset tracking approach to be 2–3 cm on average. The results demonstrated accord well with corresponding GPS measurements.

1. Introduction

As a major natural hazard, landslides cause enormous direct and indirect damage worldwide every year. Remote sensing has become the most convenient and feasible tool widely applied in deformation mapping, including in the monitoring of landslides. In the study area, due to the often limited access to Global Positioning System (GPS) measurements, and the high costs of skilled labour and instrumentation, it is difficult to collect sufficient geodetic measurements. Due to the high humidity caused by the monsoon climate of this region, optical sensors are often limited in obtaining an effective time series of measurements. Thus, microwave remote sensing using Synthetic Aperture Radar (SAR) imagery has been recognized as an effective tool for landslide monitoring. It is able to work both day and night during all weather conditions, and repeatedly acquires time series of images over large areas.

DInSAR techniques have been conventionally used for mapping of landslide activities. However, several difficulties arise when attempting to apply DInSAR in areas with steep slopes and rugged topography, high humidity, and dense vegetation cover. In addition to these difficulties, in previous studies [1,2,3], it is shown that the maximum detectable displacement gradient (DDG) of DInSAR can be exceeded in some case of very slow landslides (16 mm·year⁻¹–1.6 m·year⁻¹, as defined in Cruden and Varnes [4], Hungr et al. [5]) even when using high resolution SAR imagery.

As an alternative method, Offset Tracking (sometimes also referred to as intensity tracking) can be used to address some of the technical limitations of DInSAR, particularly the limitation of maximum detectable displacement gradient (DDG) and low coherence due to vegetation changes [6,7,8,9]. Offset Tracking allows the measurement of two-dimensional (2D) ground surface displacement with sub-pixel accuracy, by analysing the 2D offsets of the master and slave images based on cross-correlation of SAR intensity and amplitude.

Sub-pixel correlation of optically sensed imagery from spaceborne or airborne platforms has been proven as a very useful technique for investigation of landslides [10,11,12,13,14,15]. A more recent study proposed a multiple pairwise image correlation (MPIC) technique based on a sub-pixel correlation analysis of optical data [16]. This method was tested with time series Pléiades monoscopic and stereoscopic images to investigate a landslide-prone landscape in the South French Alps. It demonstrated the capability of this method to improve detection accuracy, benefiting from averaging redundant measurements from multiple pair combinations. However, in some areas, such as the Three Gorges Region where our case study is located, due to the frequent cloud cover throughout the year, it is difficult to obtain multi-temporal optical satellite images for time series analysis.

For time series offset tracking of SAR imagery, the commonly adopted approach is to use a single master image, usually the first acquisition. This simple strategy is suitable when no significant dependence is found between the number of reliable measurements and the temporal or spatial baseline. Under such a scenario, connecting offset pairs by a small baseline network has limited benefits and leads to much higher time consumption.

However, in many cases, due to a larger dynamic range of spatial baseline or temporal de-correlation effects, the number of reliable measurements decreases significantly with the increase in temporal or spatial baseline. As indicated in Yonezawa and Takeuchi [17], Offset Tracking requires similar speckle patterns between the master and slave images to obtain a sharp correlation peak. Long baseline distances will result in significant speckle geometrical de-correlation. The correlation coefficient between offset pairs decreases with the increase of spatial baseline, which leads to a higher standard deviation (STD) error in cross-correlation [18]. In addition, in densely vegetated areas, the temporal de-correlation effects are significant. Higher accuracy is required to measure very slow landslides, which again leads to lower density of final measurements. In particular, in rural areas with dense vegetation cover, there are few high-contrast surface features (e.g., artificial corner reflectors, houses, bare rocks, etc.), but a number of natural scatterers can maintain a medium correlation within a certain time period rather than over the whole time series. Thus, constructing a small baseline network based on proper thresholds of temporal and spatial baseline can help to minimize temporal and speckle geometric de-correlation effects, and take advantage of the scatterers with temporary medium correlation, so as to increase the density of measurements.

Small baseline approaches have previously been combined with offset tracking to measure large deformation magnitudes. Casu et al. proposed a PO-SBAS (pixel-offset small baseline subset) approach applied to medium resolution ENVISAT SAR data to measure large displacements (several metres) occurring in the inner part of the Sierra Negra caldera due to the October 2005 eruption [19]. The measured deformation reached one to several metres in both azimuth and range directions. Manconi et al. produced post-event deformation maps for emergency evaluation of a large, rapidly-moving (10–20 m) landslide [20]. The PO-SBAS approach was applied to ascending and descending pairs of COSMO-SkyMed images to retrieve three-dimensional (3D) deformation of the Montescaglioso landslide (Italy), of which the main movement occurred in 15–20 min at an average velocity of 0.5–1 m per minute.

For measurements of large displacement, the topographic component of offsets is not significant with regard to the deformation magnitude. Topographic distortions are usually modeled using a reference DEM and orbital data, and removed from offset results [19,20,21,22]. In the case study presented in Raucoules et al. [23], considering the selected small baselines (ranging from 1 to 200 m) with regard to the large deformation magnitude, the topographic component was neglected. In addition, co-registration errors (about 1/10 pixel size) are not significant either, in the case of large deformation.

However, in the case of much smaller displacement rates (several to dozens of centimetres per year), the residual offsets in both range and azimuth directions due to co-registration errors and orbit inaccuracies in topographic distortion removal can even obscure the real displacement, and thus are non-negligible.

This research, to the best of our knowledge, is the first to explore the use of SBAS offset tracking technique to monitor very slow landslides, in which scenario the removal of residual offsets becomes a crucial step to derive correct displacement rates even using sub-metre resolution SAR data. A step of 2D polynomial fitting is applied to both range and azimuth offset measurements to estimate and remove the residual offsets before the inversion step. Furthermore, the study area, the Tanjiahe landslide in the Three Gorges Region, China, is characterized by high humidity and dense vegetation cover on steep slopes, posing more difficulties on the application of time series InSAR and offset tracking. In our preliminary study, time series InSAR analysis of the landslide did not obtain satisfactory results. Rapid loss of phase coherence combined with topographical phase residuals lead to very low redundancy of connections (less than three per acquisition) in the SBAS InSAR network. The dense vegetation cover in this area lead to a very low density of Persistent Scatter (PS) candidates. For this reason, time series InSAR cannot provide reliable measurements. Similarly, for offset tracking, there are very few high-contrast surface features (e.g., artificial corner reflectors, houses, bare rocks, etc.) in the study area. This means this area lacks strong scatterers with constantly high correlation coefficient throughout the time series. An experiment using conventional offset tracking approach using a single master image yielded rather sparse coverage, because the number of reliable measurements decreases significantly with the temporal baseline, due to the lack of strong scatterers. Hence, SBAS offset tracking is applied to make use of scatterers showing medium correlation within a certain time period, to increase the density of reliable measurements. An assessment is then made on the potential and limitations of SBAS offset tracking in the challenging conditions.

This paper is organized as follows: Section 2 describes the study area, employed data, and proposed method; Section 3 presents the application results of this method to the Tanjiahe landslide area, followed by discussions in Section 4. Finally, some concluding remarks are reported in Section 5.

2. Materials and Methods

2.1. Study Area

The case study is carried out in the Tanjiahe landslide area in the Three Gorges Region of China. The Three Gorges Region, situated on the middle Yangtze River from Chongqing to Yichang, covers an area of 58,000 km² [24]. The terrain is composed of a succession of limestone gorges and ridges, and inter-gorge valleys. Frequent and wide distributed landslides in the Three Gorges Region have caused a lot of wasted resources, damage to properties and public facilities, and even loss of human lives. They also pose great threats to the normal operation of the Three Gorges Dam. The land cover within this region is dominated by cultivated land and mixed deciduous forest. The terrain is featured by steep slopes and dense vegetation cover [25].

The Tanjiahe landslide area is representative of the hillsides of the Three Gorges Region, sparsely populated by small villages filled with single-story buildings amongst dense orange trees. The Tanjiahe landslide area is an ancient landslide, located on the southern bank of Yangtze River with centre coordinates of 31.030°N, 110.509°E, about 56 km upstream from the Three Gorges Dam. The landslide body is underlain by mudstone, sandstone, and siltstone. The trailing edge is 432 m high. The front edge extends into the Yangtze River at an altitude of 135 m. The landslide body is about 400 m wide and 1000 m long, with a slope ranging from 10° to 25° and a volume of 9 × 10⁷ m³. The sliding direction is 340° clockwise counting from the North, predominantly towards the Yangtze River. As shown in Figure 1, the boundary of the Tanjiahe landslide looks like a boot [26,27].

The Tanjiahe landslide has not been well studied especially in the English-language literature, but some historical measurements from GPS monitoring stations can be found in a few Chinese articles. The monitoring was started in October 2006. Notable deformation development of Tanjiahe landslide was observed in 2007 [28]. By December 2009, the accumulated deformation measured from one of the GPS points (ZG289) reached 757.9 mm [26], predominantly towards the Yangtze River. By December 2015, the accumulative displacements rise up to 1800–1900 mm [29]. From 2006 to 2015, seasonal accelerations can be observed from the deformation time series plot, which is suspectedly linked to hydrological factors, such as the local rainfall and water level changes of Three Gorges Reservoir.

2.2. Data

A stack of TSX Staring Spotlight (TSX-ST) images is employed in this research supplied under data grant GEO2630 of the German Aerospace Centre (DLR), acquired in a right-looking orientation on a descending orbit over the Tanjiahe landslide area mostly at 11-day intervals. The data stack spans a time period of one year, from February 2015 to February 2016. The metadata of this annual time series of TSX-ST data is listed in

Table 1. Metadata of the data stack of TSX Staring Spotlight (TSX-ST) data using the parameters from the first image. These values remain very close for all subsequent acquisitions.

TerraSAR-X Staring Spotlight Data
First acquisition	8 February 2015
Last acquisition	28 February 2016
Satellite orbit heading (°)	189.555
Wavelength (m)	0.031
Incidence angle (°)	44.303
Polarization	HH
Range pixel spacing (m)	0.455
Azimuth pixel spacing (m)	0.169
Range resolution (m)	0.84
Azimuth resolution (m)	0.23
Maximum DDG	0.0059 (Range looks = 2)

. The estimated perpendicular baselines of all subsequent images with regard to the first acquisition are listed in

Table 2. Perpendicular baseline of each slave image with regard to the first acquisition.

Common Master	Slave
	Acquisition Date	Perpendicular Baseline (m)	Acquisition Date	Perpendicular Baseline (m)
8 February 2015	19 February 2015	391.3	27 September 2015	46.2
	2 March 2015	80.8	8 October 2015	119.4
	4 April 2015	46.8	19 October 2015	199.0
	15 April 2015	192.4	30 October 2015	12.2
	18 May 2015	42.0	10 November 2015	37.7
	20 June 2015	60.2	21 November 2015	128.9
	1 July 2015	19.4	2 December 2015	53.4
	12 July 2015	28.6	24 December 2015	28.6
	23 July 2015	147.7	4 January 2016	49.5
	3 August 2015	123.1	15 January 2016	140.0
	25 August 2015	3.5	26 January 2016	121.3
	5 September 2015	77.0	17 February 2016	252.8
	16 September 2015	122.0	28 February 2016	11.8

.

2.3. Method: SBAS Offset Tracking

We briefly summarize the SBAS offset tracking algorithm based on the work reported by Berardino et al. [30] and Casu et al. [19]. Similar to the SBAS InSAR approach proposed by Berardino et al. [30], we here consider the scenario in the amplitude domain. We assume that there is a stack of co-registered full resolution SAR data consisting of N + 1 images ${\varphi }_0,{\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_N$. Based on selected thresholds of spatial and temporal baseline, small baseline subsets are formed by $M$ data pair connections.

The 2D offset measurements of the $M$ connected pairs are represented by $\delta {\varphi }^T=\left[\delta {\varphi }_1,\delta {\varphi }_2,\cdots ,\delta {\varphi }_M\right]$, where $\begin{array}{cc}\delta {\varphi }_j={\varphi }_{ISj}-{\varphi }_{IEj}& \forall j=1,2,\cdots ,M\end{array}$, ${\varphi }_{ISj}$ is the slave image and ${\varphi }_{IEj}$ is the master image of a generic offset pair. Assuming that:

$${\varphi }_{I{S}_j}-{\varphi }_{I{E}_j}={\displaystyle \sum _{k=I{E}_j+1}^{I{S}_j}\left(t_k-t_{k-1}\right)}\frac{{\varphi }_k-{\varphi }_{k-1}}{t_k-t_{k-1}}={\displaystyle \sum _{k=I{E}_j+1}^{I{S}_j}\left(t_k-t_{k-1}\right)}{v}_k$$

(1)

where $v_k$ is the mean azimuth or range displacement velocity between time-adjacent acquisitions of a connected pair. Thus, a vector $v^T$ consist of a time series displacement velocity and can be expressed as:

$$v^T=\left[v_1=\frac{{\varphi }_1-{\varphi }_0}{t_1-t_0},v_2=\frac{{\varphi }_2-{\varphi }_1}{t_2-t_1},\cdots ,v_N=\frac{{\varphi }_N-{\varphi }_{N-1}}{t_N-t_{N-1}}\right].$$

(2)

Set $B$ as a matrix recording all connections in the small baseline network,

$$B\left(j,k\right)=\{\begin{array}{ll}{t}_k-t_{k-1},& I{E}_j+1\le k\le I{S}_j,\hspace{1em}\hspace{1em}\forall j=1,2,\cdots ,M\\ 0,& elsewhere\end{array}.$$

(3)

So, the following relationship holds

$$Bv=\delta \varphi .$$

(4)

In the vast majority of cases that $B$ exhibits a rank deficiency, the velocity vector $v$ can be retrieved by solving the over-determined equations in Equation (4) using Singular Value Decomposition (SVD), as:

$$\left[U,S,V\right]=SVD\left(B\right).$$

(5)

Then the displacement velocity vector can be derived by

$$v=V{S}^{+}{U}^T\delta \varphi$$

(6)

where

$$\begin{array}{l}S=\mathrm{diag}\left({\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_{N-L+1},0,\cdots ,0\right)\\ S^{+}=\mathrm{diag}\left(1/{\sigma }_1,1/{\sigma }_2,\cdots ,1/{\sigma }_{N-L+1},0,\cdots ,0\right)\end{array}$$

(7)

${\sigma }_i$ represent the singular values; $L$ is the number of different subsets; $N$ is the number of images in the data stack; the rank of matrix $B$ is $N-L+1$.

The step-by-step processing strategy is described as follows:

(1)

Co-registered images are cropped to cover the landslide body and the surrounding stable area. Each data pair is processed by sub-pixel offset tracking.

(a)

Topographic distortions are modeled using a reference DEM (SRTM 1 arc-second global DEM) with orbital parameters and subtracted.

(b)

The azimuth and range offsets are derived using cross-correlation. As described in Sun and Muller [3] and recalled herein, the Normalized Cross Correlation (NCC) is applied to the amplitudes of the master and slave images, to derive two-dimensional (2D) offsets. The offsets of a point in any dimension are determined by its different positions in the master and slave images. The corresponding position is determined by a measure of similarity calculated between the point-centred window in the master image and a sliding window of same pixel size in the slave image. The similarity, which is defined as the correlation coefficient, is computed as follows:

$$NCC=\frac{{\displaystyle \sum _{m=1}^{N_x}{\displaystyle \sum _{n=1}^{N_y}\left[\left(i_1\left(m,n\right)-\overline{i_1}\right)\cdot \left(i_2\left(m,n\right)-\overline{i_2}\right)\right]}}}{\sqrt{{\displaystyle \sum _{m=1}^{N_x}{\displaystyle \sum _{n=1}^{N_y}{\left(i_1\left(m,n\right)-\overline{i_1}\right)}^2}}}\sqrt{{\displaystyle \sum _{m=1}^{N_x}{\displaystyle \sum _{n=1}^{N_y}{\left(i_2\left(m,n\right)-\overline{i_2}\right)}^2}}}}$$

(8)

where $i_1$ and $i_2$ denote pre-event and post-event images with a two-dimensional offset $\left(a,b\right)$, which can be described as $i_2\left(x,y\right)=i_1\left(x-a,y-b\right)$. $N_x\times N_y$ is the correlation window size which can be modified by the application requirements. $\overline{i_1}$ and $\overline{i_2}$ are the mathematical expectation values of the cross-event image pair:

$$\overline{i_1}=\frac{1}{N_x\times N_y}{\displaystyle \sum _{m=1}^{N_x}{\displaystyle \sum _{n=1}^{Ny}{i}_1\left(m,n\right)}}$$

(9)

$$\overline{i_2}=\frac{1}{N_x\times N_y}{\displaystyle \sum _{m=1}^{N_x}{\displaystyle \sum _{n=1}^{Ny}{i}_2\left(m,n\right)}}.$$

(10)

The NCC method searches for maximum correlation (i.e., maximum similarity) between window pairs formed by the master and slave images. Those window pairs for which a maximum correlation detected is considered as corresponding pairs. After locating the corresponding pixels in the master and slave images, the 2D offsets of the slave image with regard to the master image can be obtained. To achieve a sub-pixel accuracy of correlation, image amplitudes are oversampled prior to cross-correlation. Positive values of range displacement correspond to an increase of sensor to target distance. Positive values of azimuth offsets refer to an increase of along-track displacement.

(c)

Residuals offsets due to orbit inaccuracies and co-registration errors are estimated by 2D polynomial fitting of selected reference points in the stable area, and reconstructed for the whole subset, including both the landslide body and stable area.

(2)

After correction of residual offsets, Singular Value Decomposition (SVD) is applied to invert the range and azimuth offset measurements of all connected offset pairs, to derive displacements at each acquisition time.

(3)

To discard unreliable measurements, a mask is built based on the root mean square error (RMSE) of the time series range and azimuth offset measurements, calculated pixel by pixel. For the stable area, RMSE is calculated against zero offset measurements. For the landslide area, a polynomial function is used to fit the displacement time series. RMSE is estimated between the offset measurements and the fitted polynomial. The degree of the polynomial function is selected by multiple fitting tests to obtain best goodness of fit. For the case study of Tanjiahe landslide, a third order polynomial function is used.

(4)

Time series azimuth and range offset maps can be produced to reflect the temporal evolution and spatial distribution of the landslide; time series analysis is carried out on displacement rates of selected pixels in the landslide area.

3. Results

3.1. Small Baseline Network Construction

To determine the spatial and temporal baseline thresholds to create a small baseline network, we made an experiment using the conventional offset tracking method, i.e., computing the 2D offsets of 26 offset pairs, using the first acquisition on 8 February 2015 as the common master image and neglecting any constraint of spatial baseline. All images in the data stack are cropped to the sub-area covering the landslide body and the surrounding stable ground, as shown in Figure 2. Orbital data and a reference DEM (~30 m resolution SRTM DEM) are used to model and correct the topographic components of offsets. A correlation window of 32 × 128 pixels is exploited, corresponding to a 27 m × 29 m resolution grid on the ground. The images are oversampled by a factor of 16 before the cross-correlation.

The reliability of offset measurements is assessed by their noise level on the stable ground (Figure 2), which in this case is the local variances of azimuth and range offset measurements in the stable area. This is calculated in the spatial domain using a window of 33 × 33 pixels centred by each pixel for each acquisition, each corresponding to a temporal and spatial baseline value. A proper threshold of the variances is used to select pixels of reliable measurements. Constraints of the temporal–spatial baseline are then determined based on the relationship observed between the number of reliable measurements (in pixels) and the perpendicular baseline and temporal baseline, as displayed in Figure 3.

In Figure 3a, we can see that the number of valid pixels decreases with the temporal baseline, following an approximate exponential trend. In Figure 3b, the same perpendicular baseline corresponds to varied number of reliable measurements, and no significant dependence of the number of pixels is found upon the perpendicular baseline. This suggests that the key factor affecting the number of reliable measurements is the time interval of offset pairs.

A temporal baseline of 99 days and a perpendicular baseline of 400 m are selected as constraints to construct a small baseline network. In total, 157 offset pairs are connected, with a mean connection redundancy of 5.6 per acquisition. The resulting small baseline network is shown in Figure 4, with the relative position (perpendicular baseline with respect to the first acquisition on 8 February 2015) plotted versus the temporal baseline.

3.2. Removal of Residual Offsets

Sub-pixel offset tracking is applied to each offset pair connected by the small baseline network, using the same procedure and parameters described in Section 3.1. Removal of residual offsets is carried out before inversion of the 157 offset pairs. The standard deviations over time are respectively estimated for the azimuth and range offsets measured from the stable area. By imposing a proper threshold to the standard deviations of 2D measurements, a number of pixels on the stable ground are selected as reference points for correction of residual offsets. A 2D first order polynomial function is then fitted to the range and azimuth offsets measured from these points. Using the fitted parameters, the overall residual offsets are reconstructed for the whole area, including both the landslide body and the stable area. After correction, the mean of the azimuth and range offset measurements derived from the reference points on the stable ground are estimated in the spatial domain for each offset pair, as displayed in Figure 5.

In Figure 5, we can see the mean offset measurements on the stable ground are extremely close to zero. This suggests the correction is successful.

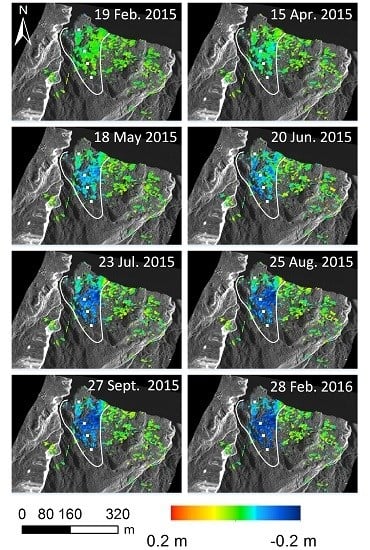
3.3. Two Dimensional Displacement Measured by SBAS Offset Tracking

After correction of residual offsets, all 157 pairs of offset measurements are inverted by SVD decomposition, to derive the azimuth and range displacement at each acquisition time. Noise-dominant pixels are discarded by a RMSE mask using the method described in Section 2.3. Displacement maps are produced to show the temporal evolution and spatial distribution of the landslide, as displayed in Figure 6 and Figure 7.

From both the azimuth and range offset maps shown in Figure 6 and Figure 7, the whole landslide body shows consistent pattern of temporal evolution, i.e., the slope experienced biggest displacement rate in April–August and tend to be stable in the following months. The spatial distribution of the landslide is also clear. The upper part of the slope shows bigger deformation magnitude, whilst smaller displacement rate is observed in the lower part of the landslide.

Three pixels on the landslide body are selected for time series analysis, with their locations displayed in Figure 8 and corresponding offset measurements plotted in Figure 9.

In Figure 9, we can see that the four pixels show quite similar magnitudes of deformation, with maximum azimuth displacement around −0.15 m, and slant range displacement ranging from 0.1 m to 0.15 m. As all these data were acquired with right-looking SAR in a descending orbit, the negative magnitude of azimuth displacement corresponds to the reverse along-track direction (predominantly to the North) and the positive magnitude of range displacement represents the movement away from the sensor. In the time series analysis, the Tanjiahe landslide shows a seasonal pattern with a big increase in the displacement rate in April–August, which slows down in the remainder of the year.

3.4. Precision Assessment and Comparison with GPS Measurements

The precision of offset measurements is assessed as follows: as the accumulated 2D displacements on each acquisition date have been retrieved, for each valid pixel in the stable area, the standard deviation errors over time of accumulated azimuth and range offset measurements are calculated respectively. The overall error level is estimated by spatially analysed statistics in terms of ‘mean ± STD’, as shown in

Table 3. Overall precision assessment based on the standard deviation errors of the azimuth and range offset measurements derived from the stable ground, calculated along the temporal baseline.

	Azimuth Offset (m)	Range Offset (m)
Standard deviation errors	0.025 ± 0.011	0.027 ± 0.009

.

Due to the absence of direct geodetic measurements of the landslide, we compare the deformation magnitudes of the selected pixels derived by the offset tracking approach with GPS measurements found in literature. Four GPS stations were installed along the longitudinal section of the Tanjiahe slope (ZG287, ZG288, ZG289, and ZG290) and surveyed monthly [29]. The paper presented a schematic view of the GPS stations, a table showing annual displacement magnitudes from 2007 to 2015, as well as a plot of GPS displacement curves. The displacement time series of the four GPS stations show a very consistent pattern of accumulated displacement. Smaller deformation magnitude is observed from the ZG290 station located at the lower part of the slope, whist higher displacement rate is found on the three GPS stations installed on the upper part of the slope (i.e., ZG287, ZG288, ZG289). This distribution is identical to the spatial distribution revealed by the offset maps in Figure 6 and Figure 7.

We have no access to the coordinates and actual measurements of the GPS time series used in the abovementioned publication [29] (the plot in Zhang et al. [29] does not give the digit corresponding to each point of the GPS time series). Nevertheless, we manually aligned the schematic view of the GPS locations to the geocoded SAR amplitude over the Tanjiahe landslide area, using the river shoreline as the matching features. In this way, the sketch maps of GPS stations are coarsely co-registered with the offset tacking results. Then the pixels in the same area of GPS stations are extracted for a comparison. The GPS time series plot was taken from the publication [29] and digitized, in order to obtain the GPS measurements corresponding to the curves in the plot. The GPS measurements span the time period from December 2014 to December 2015, overlapping 10 months in time with the offset measurements (February 2015–February 2016).

Prior to the comparison, the GPS time series measurements are projected onto the azimuth and slant range directions, based on the knowledge of the main sliding direction of the landslide (340 degrees clock-wise from the North), and slope degrees of each position derived from the reference SRTM DEM. The projected GPS monthly measurements are interpolated to the acquisition dates of each image in the TSX data stack, in order to make the time series comparison on a one-to-one basis.

The time series of pixels located in the same area of the GPS stations are plotted against the annual displacements of individual GPS stations, as shown in Figure 10. As ZG290 and ZG287 are located out of the mask of valid pixels, the other two stations, ZG288 and ZG289, are used in the following analysis.

In Figure 10, we can see the time series offsets measured from pixels located on the positions of ZG288 and ZG289 closely follow the corresponding GPS measurements; the differences between the offsets and GPS time series are estimated by RMSE, and summarized in

Table 4. The root mean square error (RMSE) between the time series displacements measured by SBAS offset tracking and GPS stations.

	ZG288	ZG289
Azimuth RMSE (cm)	1.89	1.20
Range RMSE (cm)	3.38	1.80

. Considering the precision of SBAS offset tracking (as estimated in Table 3) of 2.5 ± 1.1 cm in the azimuth direction and 2.7 ± 0.9 cm in the range direction, the RMSE between the offset time series and GPS data are not statistically significant.

4. Discussion

4.1. The Relationship between the Landslide and Water Level Variations of the Three Gorges Reservoir

The construction of the Three Gorges Dam was started in 2003 and completed in 2009. The reservoir level rose from 66 m to 135 m in 2003, then to 156 m in 2006, and finally to 175 m above sea level after three impoundments. After reaching the designed maximum height of 175 m in 2010, the water level experiences 30 m of fluctuation between 145–175 m every year. A drawdown-filling cycle is repeated every year at almost exactly the same time.

As is well known [31,32], the ground water table or pore-water pressure within the soil layers of the landslide body are affected by the reservoir surface fluctuation and local precipitation, which decreases the effective normal stress leading to a decrease in shear strength of the soils. In previous studies, the fluctuation of the reservoir water level and seasonal rainfall are found as the two main triggering factors for landslides along the Yangtze River banks [31,33,34,35,36]. Two studies of the Tanjiahe landslide show controversial results on whether the local rainfall is the key driving factor of the slope movements in this area [29,37]. However, previous studies of the Ivancich landslide in central Italy point out there is a lack of correlation between the rainfall and the extremely slow landslide displacement (<16 mm·year⁻¹) [38,39,40]. Thus, in this section, the landslide displacement is respectively compared with reservoir water level measurements and daily rainfall data. The rainfall data was measured from a gauge station in Badong County, 16 km upstream from the Tanjiahe landslide site.

It should be noted that the time series measurements of azimuth and range offset are not evenly spaced in the time domain, as some acquisition dates are missing. Thus, prior to the analysis, a cubic spline interpolation is used to interpolate across the missing dates for the every-11-day measurements. The interpolated displacements of the three selected pixels ‘P1’, ‘P2’, and ‘P3’are displayed in Figure 11 as follows.

As we can see from Figure 11, the measurements from all three pixels show a consistent pattern of displacements in both the azimuth and range directions. The azimuth offset measurements of ‘P1’ are then selected for subsequent analysis in Section 4.1.

The every-11-day offset measurements with a corresponding trend line are plotted against the water level measurements (Figure 12) and local rainfall data (Figure 13).

In Figure 12, a significant and abrupt increase in deformation magnitude can be observed, synchronized with the sharp reservoir drawdown in April–July 2015, and non-significant displacement (with regard to the 2–3 cm precision of azimuth offset measurements) over the following months. It is evident that the active landslide period coincides with the fast drawdown of the reservoir water level. No noticeable correlation is found between the dramatic raising of water level in September–October and the landslide displacement.

In Figure 13, heavy and intense rainfall is observed from March to October, covering the period of the greatest displacement rate (April–July 2015). However, in the period of July–October 2015 with intensity of rainfall second only to the previous months, no noticeable deformation can be observed.

The above results suggest that rainfall does not play a key role in triggering the landslide in the observation year, but we cannot rule out the possibly that rainfall has combining effects with the water level variations due to the overlapped period of reservoir fast drawdown and heavy rainfall. Reservoir drawdown is the key driving factor of the landslide. It appears that the slope stability decreases with the fast drawdown of the reservoir water level and increases with the big rise of water level.

4.2. Potential and Limitations of the SBAS Offset Tracking Approach in Comparison with InSAR

Sub-pixel offset tracking techniques only utilize intensity bands of the satellite imagery to retrieve 2D ground deformation. It is less sensitive to low coherence and does not require phase-unwrapping, which leads to most of the failures in time series InSAR due to the low density of valid pixels. As a method free of phase-unwrapping, offset tracking has no limitation in the maximum detectable displacement gradient (DDG). Thus, offset tracking techniques potentially have the capability and advantage to measure slope movements with the speed exceeding the maximum detectable displacement of DInSAR or map deformation in challenging areas such as densely vegetated and steeply sloped terrain.

For a single pair of SAR images, the accuracy of offset tracking is jointly determined by the deformation rates in the area of interest, image resolution, and the correlation coefficient of scatterers in the target area [41]. The presence of high-contrast surface features does help to improve the accuracy. With the availability of high-resolution SAR imagery, offset tracking is able to monitor very slow-moving landslides (16 mm·year⁻¹–1.6 m·year⁻¹ as defined in Cruden and Varnes [4], Hungr et al. [5]) and complement the applications of DInSAR. This has been demonstrated in our previous study of the Shuping landslide [3].

Given an area of interest and the same dataset, the accuracy of offset tracking is mainly determined by the correlation coefficient. Low correlation leads to a large uncertainty in cross-correlation and eventually low accuracy of measurements. For this reason, temporal and spatial baseline screening is necessary prior to analysis. If there is a significant dependence between the number of reliable measurements and the temporal–spatial baseline, it is beneficial to create a small baseline network of offset pairs, in order to increase the density and coverage of observation.

The proposed SBAS offset tracking approach is demonstrated of being capable of measuring centimetre-level landslide rates in densely vegetated terrain. Instead of only measuring the deformation of only a few sparsely distributed strong scatterers, the proposed approach provides a synoptic overview of the landslide by constructing a small baseline network and time series inversion of redundant connection of offset pairs. According to the results of our preliminary experiment in conventional offset tracking, to achieve the same precision, the number of reliable measurements derived by SBAS offset tracking is more than 15 times the conventional offset tracking method.

Offset tracking has the advantage of obtaining 2D measurements using data from a single orbit. It should be noted that the azimuth and range offsets only measure the projection of the real displacement on the slant range plane due to the radar geometry. The displacement component perpendicular to the slant range plane, if there was any, would not be detected. To measure 3D displacement, images from at least two different orbits are needed to solve the least squares functions. Data from descending and ascending orbits are preferred to improve the robustness of the estimation, which should be considered when selecting new data in future studies.

East-West (E-W)-oriented landslides provide a better geometry for line-of-sight (LOS) measurement from sun-synchronous SAR imaging instruments, as the E-W and downward component of the sliding vector can both be captured by satellite LOS measurements. For North-South (N-S)-oriented landslides, as most of the landslides on the banks of Yangtze River appear to be, Offset Tracking is of great importance to provide measurements in the azimuth direction (approximately N-W) when repeat data are only available from a single orbit.

InSAR techniques have been widely used for displacement monitoring in many areas including the Three Gorges Region, with success demonstrated through measurements of much smaller displacement rates in urban areas using time series InSAR approaches [42,43]. This case study, shows results of so-called ‘very slow-moving’ landslide (16 mm·year⁻¹ to 1.6 m·year⁻¹ as defined in Cruden and Varnes [4]) with annual displacement rates up to 20 cm. As calculated in Table 2 using a multi-looking factor of 2, the upper limit of measurable displacement in one repeat cycle (11 days), is 0.59 cm, over a ground distance of 1 m. For the Tanjiahe landslide showing a dramatic increase in deformation over a short period, there is a high probability of underestimation by InSAR based techniques, especially on the landslide boundary.

In addition to the limitation of maximum detectable displacement gradient (DDG), the rapid loss of phase coherence is a major issue in densely vegetated areas. In our preliminary work, using the TerraSAR-X Staring Spotlight data with an 11-day repeat cycle and 0.23 m × 0.84 m resolution, the coherence loss is still a problem, resulting in too low a redundancy of data connections to apply time series InSAR. Satellite data with a shorter re-visit cycle and high resolution (1–3 m at least) is expected can help to address this issue, which should be exploited in future work. A shorter repeat interval is much-needed by DInSAR in this kind of study area. The improvement of the re-visit time will also increase the maximum measurable displacement of DInSAR.

Geometric distortion is also a key factor affecting the quality of interferograms, especially in an area characterised by many steep slopes. DEM products often exhibit higher height errors in areas with rugged topography due to geometric distortions. Low resolution, inaccuracies, or both in the reference DEM can lead to large residual errors of topographic phase, which further decrease the quality of interferograms.

Theoretically, time series InSAR has higher accuracy (millimetre-level) compared with Offset Tracking (centimetre-level). In other types of terrain (e.g., with more man-made structures, less vegetation, or lower slopes), the use of InSAR techniques may have more advantages for displacement monitoring, especially for slower displacement.

For slow-moving landslides, the use of offset tracking is recommended to assess if the assumption of maximum displacement gradient of InSAR can be fulfilled. Offset Tracking is less sensitive to low coherence and is able to derive 2D displacement using data from a single orbit, whilst time series InSAR can help to detect the smaller magnitude of deformation (e.g., during a less active period of the landslide). Thus, the two techniques are complementary to each other and there appears to be hope of more improvements with the availability of satellite data of shorter revisit cycle and higher resolution.

5. Conclusions

This work demonstrates the capability of the SBAS Offset Tracking approach to monitor centimetre-level landslide displacement in a challenging area characterised by dense vegetation cover and steep slopes. In the case study of the Tanjiahe landslide, as significance is found between the number of reliable measurements and the temporal baseline, a small baseline network of offset pairs is created to minimize temporal decorrelation, and increase the density and coverage of the offset measurements at the end. Considering the centimetre-level displacement rate, an extra step is taken to remove the residual offsets due to co-registration errors and orbit inaccuracies before the SVD inversion of all offset pairs. Taking advantage of the sub-metre resolution of the TSX Staring Spotlight data, the proposed SBAS offset tracking approach has been shown of being capable of measuring centimetre-level landslide rates with an average precision of 2–3 cm, with point density more than 15 times of the conventional offset tracking approach. The offset results have been validated of good agreement with published GPS measurements. This approach is of particular interests for deformation monitoring in many rural areas lack of high contrast surface features, especially over densely vegetated and steep terrain.

In the case study, the relationship between the landslide and local rainfall, as well as the water level changes of the Three Gorges Reservoir has been assessed. The reservoir fast drawdown is identified as a major triggering factor of the landslide, and rainfall does not appear to be a key triggering factor in the observation period.