Performance Assessment of Tailored Split-Window Coefficients for the Retrieval of Lake Surface Water Temperature from AVHRR Satellite Data

Abstract

Although lake surface water temperature (LSWT) is defined as an essential climate variable (ECV) within the global climate observing system (GCOS), current satellite-based retrieval techniques do not fulfill the GCOS accuracy requirements. The split-window (SW) retrieval method is well-established, and the split-window coefficients (SWC) are the key elements of its accuracy. Performances of SW depends on the degree of SWC customization with respect to its application, where accuracy increases when SWC is tailored for specific situations. In the literature, different SWC customization approaches have been investigated, however, no direct comparisons have been conducted among them. This paper presents the results of a sensitivity analysis to address this gap. We show that the performance of SWC is most sensitive to customizations for specific time-windows (Sensitivity Index SI of 0.85) or spatial extents (SI 0.27). Surprisingly, the study highlights that the use of separated SWC for daytime and night-time situations has limited impact (SI 0.10). The final validation with AVHRR satellite data showed that the subtle differences among different SWC customizations were not traceable to the final uncertainty of the LSWT product. Nevertheless, this study provides a basis to critically evaluate current assumptions regarding SWC generation by directly comparing the performance of multiple customization approaches for the first time.

1. Introduction

1.1. Accuracy of Satellite-Based Acquisition of Lake Water Temperature Measurements

Lake surface water temperature (LSWT) has been identified by the global climate observing system (GCOS) as one of the essential climate variables (ECV) [1]. Consequently, there is ongoing interest to monitor this variable to detect long-term trends. Water temperature is not only an important ecological parameter in lacustrine eco-systems [2], it can also serve as a proxy for detection of local climate change [3]. Studies have revealed global warming trends for LSWT within different climate zones (e.g., [4,5]), and there is evidence that indications of climate change are sometimes even stronger within lake than in air temperature records (e.g., [6,7]). To further explore these trends on a continental or even a global scale, there is a need to generate accurate and homogeneous LSWT time series from different climatic regions. The World Meteorological Organisation (WMO) recommends that time series prepared for climate studies should ideally consist of data records that exceed 30 years.

Traditionally, lake water temperature monitoring is based on in-situ measurements acquired from individual lakes. Thus, the availability of measurement data is often restricted to point-based locations, and limited to a specific duration. Moreover, a range of measurement methods have been applied to retrieve these in-situ records (e.g., based on the use of different instruments, defined measurement depths, etc.). This heterogeneity in terms of data coverage and retrieval methods hampers the detection of climate signals within individual lakes and even more notably when comparing climate signals associated with different lakes.

Satellite-based temperature measurements overcome these limitations. The data is spatially and temporally homogeneous and is acquired with a consistent measurement method across the defined regions of interest. They can be used to create independent time-series datasets, to complement existing in-situ temperature records or to merge different datasets by serving as a relatively more robust and extensive baseline record. The advanced very high-resolution radiometer (AVHRR) sensors provide thermal infrared (TIR) data at two separate wavelengths, from NOAA-satellites since the early 1980s and from EUMSAT MetOp-satellites since 2002. Consequently, time series data that spans more than 30 years is available. The potential to generate extensive and temporally homogeneous time series provides motivation to further improve AVHRR data processing methods.

However, the accuracy of LSWT retrieval from raw satellite data depends on many factors. Many sources along the processing chain contribute to the aggregated uncertainty associated with the final data product [8]. The retrieval method itself (accounting for atmospheric correction), hardware/sensor-related uncertainties, and uncertainties from different sources along the processing chain (cloud screening, geolocation, resampling, and calibration) are all known sources of contribution. Furthermore, the accuracy of LSWT retrieval from satellite data strongly depends on the characteristics of the target lake defined by its local properties (climate, latitude, altitude) and its morphology (depth, size, flow dynamics) [9,10].

Under optimal conditions and with careful post-processing, an accuracy of <0.5 K can be achieved [11,12,13]. However, the accuracy target of 0.2 K, mentioned by GCOS for satellite-based lake water temperature retrieval [14], is still beyond the capabilities of current LSWT retrieval methods for earth observation data. Furthermore, even the more realistic accuracy target of 0.5 K (with a threshold of 0.8 K) required for the operational sea surface temperature and ice analysis (OSTIA) product used in numerical weather predictions at the European Centre for Medium-Range Weather Forecasts (ECMWF) [15], is difficult to achieve [16]. In general, validation studies of automated retrieval methods designed to be used with data from multiple inland water bodies are in general not yet able to reach the 0.5 K accuracy target [13,17,18,19,20,21]. The best results have been achieved with AATSR (0.56 K [13]) and ATSR-2 (0.47–0.64 K [17]) sensors. Operational accuracies associated with AVHRR and MODIS sensors range between 1 K and 2 K in comparison [18,19,20,21].

The first part of this study, focuses on optimizing the split-window retrieval method itself. Thus, only the correction of the atmospheric attenuation of the TIR signal along its path from the earth’s surface to the top-of-the-atmosphere (TOA) is analyzed. Other sources of uncertainty from the pre- and post-processing of the data (e.g., geo-referencing, instrument calibration, cloud filtering, skin-bulk temperature conversion, etc.) are not addressed within the scope of this study. We hypothesized that the more we tailor the retrieval method to specific atmospheric conditions, the higher the associated accuracy. However, this would also effectively restrict the applicability of the method to a wider range of scenarios. We compared the performances of different customized retrieval methods to identify reasonable and optimal trade-offs between accuracy and the applicability of the respective methods to a range of scenarios.

The second part considered the implications of the results from the first part of the study within the whole processing chain (i.e., starting from data preprocessing to the generation of the final LSWT product). This procedure evaluates the impact of different tailoring approaches on the overall accuracy of the processing chain. Firstly, the different resultant AVHRR LSWT products were validated against in-situ data to determine if the inherent SWC uncertainty could be effectively linked to the overall uncertainty. Secondly, a theoretical analysis with a simple error propagation model was conducted to estimate the impact of different tailoring methods with respect to different sensors (e.g., (A) ATSR, MODIS, and AVHRR).

1.2. The Satellite-Based LSWT Retrieval Method

The split-window approach is based on making use of the different absorption characteristics of water vapor between differential TIR spectral windows [22]. Two algorithms are currently applied in various applications. The multi-channel SST (MCSST) [23] assumes that there is a linear relationship between the atmospheric transmittance of the signal and the difference in absorption between the two channels. The non-linear SST (NLSST) used with NOAA SST products [24] improves the accuracy particularly for day-time measurements [25], because it considers the non-linear nature of atmospheric absorption processes. However, when adapted and applied to inland water bodies, no significant improvement was found with NLSST rather than with the MCSST algorithm [13,26,27]. Thus, we use the well-established MCSST-based split-window method (Equation (1)) with radiative transfer modelling for synthetic matchup generation. This was previously applied in [13,19].

$$T_{LSWT}=a_0+a_{1}B{T}_4+a_2\left(B{T}_4-B{T}_5\right)+a_3\sec \mathsf{\theta }\left(B{T}_4-B{T}_5\right)$$

(1)

• $a_{0,1,2,3}$ split-window coefficients (SWC)
• $B{T}_{4,5}$ brightness temperature from AVHRR bands 4 and 5
• $\mathsf{\theta }$ satellite’s view zenith angle (VZA)

1.2.1. Empirical Matchup Data for SWC Generation

The split-window coefficients (SWC) in Equation (1) are empirical coefficients, which are determined by multi-linear regression with a set of empirical matchup data (hereafter referred to as matchup data). The selection and the quality of the matchup data is of crucial importance, as the accuracy associated with the MCSST retrieval approach depends on the quality of the split-window coefficients. The matchup data is comprised of simultaneously taken measurements of the same feature. Each pair contains a TOA measurement from the satellite, and a coincident measurement at the earth’s surface (in-situ measurement).

Current sea surface temperature (SST) products use in-situ data from buoys, which are distributed in the oceans around the world, to determine globally valid coefficients. However, buoy data is often sparse or unavailable. While other in-situ measurement data from stations near the shore can be used instead, such data does often not adequately represent the LSWT of open water. Especially when temperatures are measured in shallow waters or within semi-isolated areas like narrow bights or harbors.

An alternative to in-situ data is the use of synthetic matchup data generated by radiative transfer modelling. This has been successfully applied and validated in recent studies (e.g., [13,17,19]). The idea is to generate matchup data using a radiative transfer (RT) model. The RT model ingests atmospheric profiles from NWP re-analysis to yield the brightness temperatures as observed by the satellite’s sensors for any given surface temperature. This underlying concept offers the advantage of generating a synthetic dataset that is independent of the quality and availability of in-situ data. Moreover, synthetic matchup data can be generated in large quantities, which offers more flexibility to produce tailored SWC.

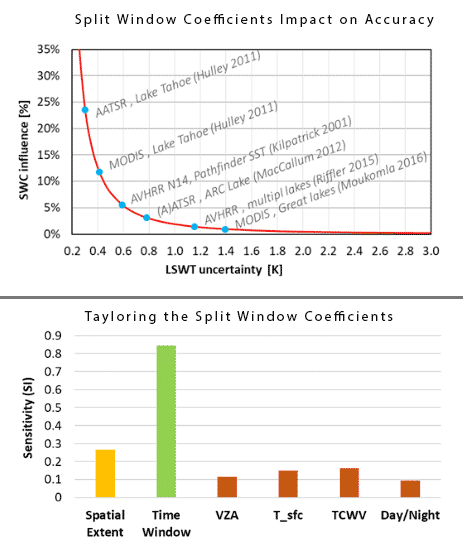
1.2.2. Tailoring the Split-Window Coefficients

The SWCs are derived from the polynomial split-window equation (Equation (1)) by regression, using empirical pre-calculated matchup data. Thus, the SWC are tailored to and valid for situations that they were trained for, using the matchup data. For example, if only matchup data with surface temperatures below 5 °C are used to train SWCs, then the applications of the resulting coefficients are limited to cases with comparable surface temperature. While highly tailored SWC have limited ranges of applicability, they yield results with greater accuracy.

The concept of reducing the validity of SWC across a wider range of conditions to improve their performance under appropriate scenarios has been successfully applied in various studies. For example [13,19] spatially restrict the coefficients’ validity to lake specific coefficients; the MODIS product uses two sets of coefficients [28], each tailored to different ranges of water vapor; and the Pathfinder algorithm [29] uses temporally-tailored monthly coefficients combined with coefficients tailored to different water vapor ranges. The contrary can also be done to simplify and maximize the utility of derived SWC under a wider range of conditions. For instance, Hulley et al. [13] assumed that all of the atmospheric states at a local point are covered within year of matchup data, such that the coefficients are universally valid with respect to time.

While all of these SWC tailoring approaches have proven merits, it is uncertain as to which approach is associated with better relative performance with respect to the others. This study addresses this knowledge gap by quantifying and comparing the relative performance related to the most important types of SWC tailoring approaches. A sensitivity analysis is conducted with data from five different regions. This quantification exercise supports the direct comparison of the coefficients’ intrinsic errors, and effectively highlights the main sources of SWC related uncertainties.

2. Data and Study Sites

2.1. Study Sites

The sensitivity analysis was performed independently for five different areas located in different regions of Europe. The areas are circular, with a maximum radius of about 500 km around a center. From north to south, the sites include Northern Scandinavia (NSC), Southern Scandinavia (SSC), Eastern Europe (EEU), the Alps (ALP), and a Mediterranean region around Greece (GRE), as shown in Figure 1. In general, the climate is dryer and colder towards the north, and it transitions from a more maritime climate in the west to a more continental climate regime in the east. At northern latitudes, the total atmospheric column contains less water vapor than in the south (Figure 2), whereas the cloud cover rate is higher in the northern latitudes (Figure 3). For example it can be observed that there is an approximately 50% probability of >90% cloud coverage over the NSC, whereas around 15% over Greece. Temperature retrieval based on TIR radiation requires clear sky observations. Since clouds are opaque with respect to TIR wavelengths, and therefore they are excluded from the matchup data.

The NSC site extends over Norway and Sweden in the west, Finland in the center and Russia in the east. The topography is rather flat and homogeneous for the majority of the region. However, at the north-western edge the Norwegian mountains elevates to about 1500 m a.s.l.; these features act as an orographic barrier against prevailing westerly weather conditions. The region is generally colder and dryer than the other regions due to its latitude and to the decreasing influence of the Gulf Stream. Even though the total column of water vapor in the atmosphere is low and stable (Figure 2), the region has a high rate of cloud cover, which significantly reduces the number of suitable satellite observations (Figure 3).

The SSC site extends over Norway, Sweden and Denmark, and parts of the Baltic Sea. The topography is flat towards the south-east and mountainous towards the north-west, with elevations reaching 2600 m a.s.l. The topographic features form an orographic barrier like that observed in the NSC site, resulting in dryer conditions over Sweden. On the other hand, the notable influence of the Gulf Stream leads to a generally warmer and more humid climate over the whole region. The cloud cover rate is, as for NSC, high and consequently reduces the number of clear sky observations (Figure 3).

The EEU site extends mainly over Poland, Hungary, Slovakia, Romania and Ukraine. The hilly and mountainous topography is dominated by the Carpathian ridge, and the highest elevations reach over 2600 m a.s.l. The continental climate is characterized by pronounced seasonal patterns, especially with respect to temperature differences. The atmosphere is generally drier and less influenced by short term weather dynamics induced by the moisture influx of the sea.

The ALP site extends over Germany, France, Italy, Austria and Switzerland. The pronounced topography ranges from a few meters a.s.l. in the Po-Basin to over 4000 m a.s.l. in the Alps. The region is characterized by the alpine ridge, which acts as a strong orographic barrier that separates the north and the south into two distinct climatic regions. Whereas the north is generally colder and has a slightly more continental climate, the south is strongly influenced by the warm Mediterranean Sea and its important moisture influx to the atmosphere (Figure 2).

The GRE site extends over the Balkans, southern Italy, Greece, Bulgaria and parts of the Mediterranean Sea. It is the most heterogeneous one of the five regions, not only in terms of topography but also in terms of land/water transition. The hilly yet mountainous topography on the main land reaches elevations of over 2900 m a.s.l. in the Olympus mountain range, and it includes parts of the Ionian Sea, the Aegean Sea and a large quantity of small islands. The warm Mediterranean climate provides a constant supply of water vapor from the sea, along with an increased storage capacity for water vapor in the atmosphere. The combined effect results in elevated absolute humidity rates (Figure 2), and relatively low cloud coverage over the GRE region (Figure 3).

2.2. Generation of Matchup Data

To generate the matchup data, the fast radiative transfer model for TIROS operational vertical sounder (RTTOV) v.11 [31] was used. The model is known to be capable of producing highly accurate results efficiently. The RT-model was fed with atmospheric profile data extracted from the ECMWF ERA-INTERIM reanalysis data ([30]). The ERA-INTERIM dataset is a global atmospheric reanalysis dataset with spatial resolution of about 80 km grid cells and a temporal resolution of 6 h. The dataset was designed to be used in climate studies (i.e., long-term stability), and has a temporal extent that covers the entire period where AVHRR-2 and -3 data is available (i.e., 1979 to the present day).

For this study, the atmospheric profiles and ground parameters were extracted for every grid cell within the five regions at a six-hour time step for a period of four years (2002–2005). This produced meteorological dataset with over 3.5 M atmospheric profiles and corresponding ground data. For each of these atmospheric profiles, the RT-model was run 40 times to include satellite view zenith angles (VZA) between 0° and 60° and surface temperatures between −5 °C and 35 °C. A total of over 142 M radiative transfer model runs were conducted to create the match-up database, with a distinct matchup pair being produced with the completion of each run.

2.3. Validation Data

The final validation was performed for a four-year period (2004–2007), by comparing satellite-derived LSWT with in-situ measurements at Lake Constance and Lake Geneva. Pre-processed AVHRR data from NOAA-17 archived at the Remote Sensing Group of the University of Bern [32] was used for the validation. The derived LSWT product was compared to hourly in-situ measurements from Lake Geneva and Lake Constance for the whole test period. The measurements made at Lake Geneva were recorded at a location (46.458°N, 6.399°E) about 100 m from the shore and 1 m below the water surface. The measurements at Lake Constance were taken in the Lindau Harbor (47.544°N, 9.685°E), at a depth of 0.5 m.

3. Method

3.1. Sensitivity Analysis

For the sensitivity analysis (SA), the ‘one-at-a-time’ or ‘local’ approach (e.g., [33]) was used such that only one input variable was modified at a time while the others remained constant at their baseline values. The initially modified input variable is then reset to its baseline value, and the same procedure is repeated for each of the other input variables. With this approach, any observed change in the output can be ascertained to the specific input variable that was modified in isolation. A quantitative comparison of the impacts of the input variables is possible as each variable is explored from the same starting point (baseline).

To quantify the performance of the variables of interest with the SA, the intrinsic error of the SWC is used as performance indicator. The intrinsic error is equal to the regression error, which is the standard deviation (SD) between the matchup data and the mathematical model (Equation (1) parametrized with the SWC). Furthermore, a sensitivity index (SI) is computed for each parameter. The SI is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value.

For each SWC customization approach, a different sub-set of the matchup data base was chosen to regress the coefficients. The filter to select the matchup data used for the coefficients regression translates into the parameter space during which is explored during the SA. The SA is performed on the six parameters expected to be the most influential; the ranges of values associated with each parameter is summarized in

Table 1. Overview of the parameters and the associated range of values explored with the sensitivity analysis. Baseline values are bold.

Parameter	Units
Time window	[days]	1	2	4	7	14	30	90	180	360	720
Spatial radius	[km]						50	90	125	200	300	400	550
VZA range	n bins						1	2	4	10
Sfc Temperature	n bins						1	2	4	10
TCWV	n bins						1	2	4	10
Day/night separation	true/false						false	true

. We also assume that all of the input variables are independent, and any correlations are considered to be negligible. While this assumption is not entirely true, the potential correlations are considered to be weak, and will not significantly affect the outcome of the SA.

The baselines for the time window and the spatial radius are chosen based on the results of a preliminary analysis, which was conducted, but excluded from this paper for the sake of brevity. The baseline for the view zenith angle was chosen based on values reported in the literature (see below), and the baseline values for the other variables is set to ‘all’. This effectively includes all realistic values without constraints.

The spatial extent (radius R in km) is defined as the region where the same set of coefficients can be applied without substantial loss in accuracy. If such a region is circular, the size of the region can be expressed by its radius R (i.e., distance from the center to the edge of the circle). The SA explores different spatial extents within R = [0, 500] km. While the maximum radius of 500 km is associated to a rather small region, the preliminary analysis showed that errors stabilized for distances exceeding 1000 km. Consequently, R_max was set to 550 km. The baseline value for the region size was fixed at R = 50 km, which was identified as a good trade-off from the results of the preliminary analysis.

The time window is defined as the interval (in days) within which a set of coefficients remains valid without substantial loss in accuracy; it is dependent on the stability of the atmospheric conditions over time. Time window intervals between one day and two years were investigated. Based on the results of the preliminary analysis, a baseline value of 30 days was selected.

The view zenith angle (VZA) is an important factor that affects the accuracy of coefficients. It defines the length of the path a signal must travel through the atmosphere, and also the strength of the emitted signal (i.e., directional emissivity). These effects are supposed to be accounted for by the formulation of the retrieval method (i.e., the VZA dependent term in Equation (1)). However, a significant decrease in accuracy can be observed at larger VZAs around 45–60 degrees. The VZA parameter is represented by the number of equal sized bins with which the VZA range between 0 and 60 degrees is divided. Thus, three VZA bins means that we compute three sets of coefficients, one of each that is applicable for lower, medium, and high VZA, respectively. The VZA is not limited to a defined threshold; the whole range of available data from nadir to about 58 degrees is explored. The baseline is using only one bin, meaning that there is only one set of coefficients covering the whole range of VZA.

The surface temperature (Tsfc) is the temperature of the emitting body. It determines the strength of the emitted signal at the earth’s surface and also influences the emissivity itself [34]. Similar to the VZA limit, the parameter represents the number of bins that is applied to split the range; the result is then applied to separate coefficients. The baseline is one Tsfc bin, which means that a single set of coefficients covers the whole range of Tsfc values.

The water vapor content (total column of water vapor, TCWV) in the atmosphere absorbs electromagnetic radiation in the TIR. Consequently, its influence on the coefficients quality is of interest. Like for the VZA bins and the Tsfc bins, the parameter defines the number of distinct ranges into which the range of possible water vapor content values is divided. The baseline is one TCWV bin, meaning that there is only one set of coefficients covering the whole range of TCWV values.

The time of the day is used to generate specific coefficients for day-time and night-time temperature retrieval. The ERA-INTRIM reanalysis dataset provides data four times a day at 0 h, 6 h, 12 h and 18 h. Two variations with and without the separation of day/night coefficients were set up in this study. Day and night-time is defined by the sun zenith angle, where five degrees over the horizon is defined as daytime and 5 degrees below the horizon is considered as night-time. The twilight period in between the two defined periods of time is excluded in this study. The variant without distinction between day and night was selected as the baseline.

3.2. Validation

Based on the results from the sensitivity analysis, different sets of coefficients are generated and applied to a set of satellite data. Thus, for each set of SWC, a LSWT time-series is derived, and compared to the available in-situ data collected from Lake Geneva and Lake Constance. Both temporal and spatial matches were identified to compare the two types of measurements. From each satellite scene, the average of all pixel values within a 5 km radius around the in-situ measurement location is taken to calculate the satellite-based LSWT value. This value is then compared to the in-situ measurement with the closest time stamp to the satellite overpassing time, and within a 2 h temporal window.

3.3. Uncertainty Propagation Analysis

The LSWT processing chain includes many sources of uncertainties. These uncertainties are propagated and aggregated in the final LSWT product. To estimate the influence and the relevance of the SWCs’ intrinsic uncertainty, a model that quantifies the amount of error that is propagated throughout the processing chain is needed. In this study, the uncertainty analysis is limited to the relationship between the total amount of uncertainty and the SWCs’ intrinsic uncertainty. Therefore, the error propagation model can be simplified by assuming that only the combination two sources contribute to the total uncertainty, namely the SWCs’ intrinsic uncertainty (σ_SWC) and the auxiliary uncertainty (σ_aux). The latter is a factor that combines the cumulative effect of all uncertainties in the processing chain, excluding the SWCs’ intrinsic uncertainty. To further simplify the problem, the two sources are assumed to independent from each other, and having a Gaussian uncertainty distribution. A simple error propagation model can be applied under the aforementioned assumptions; the model is described by Equation (2) [35,36], and is applied to estimate the influence of the SWCs’ intrinsic uncertainty on the total uncertainty.

$${\sigma }_{tot}=\sqrt{{\sigma }_{SWC}{}^2+{\sigma }_{aux}{}^2}$$

(2)

• ${\sigma }_{tot}$ Total uncertainty of the LSWT product;
• ${\sigma }_{SWC}$ uncertainty issued from the SWCs regression;
• ${\sigma }_{aux}$ uncertainty from all other sources expect from the SWCs.

From the sensitivity analysis, the range of expected SWC intrinsic uncertainty values is known, and the total uncertainty is determined from the LSWT product. Hence, the influence of SWCs’ intrinsic uncertainty on the total uncertainty of any validated LSWT product can be determined. Likewise, this can also be determined for data derived from other sensors using the same retrieval method.

4. Results

4.1. Results of the Sensitivity Analysis

4.1.1. Region Size

The effect of region size on the SWC depends on the study region. In general, the intrinsic error associated with the GRE site is the highest, followed by the error associated with the EEU, ALP sites, and lowest in the SSC and NSC sites (Figure 4).

This observation is expected, as regions with higher temperatures are supposed to have more dynamic atmospheric conditions, which are linked to higher SWC uncertainties.

However, the sensitivity of SWC to region size is strongest in NSC (Sensitivity Index, SI of 0.51), followed by the ALP (0.40), and GRE (0.31). SWC sensitivity to region size is limited in both the EEU (0.05) and SSC (0.06) sites; the results are summarized in

Table 2. Overview of the intrinsic errors (in degrees of K) for each region, with respect to variable radius values. The sensitivity index (SI) is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value (i.e., radius of 50 km).

	SI (-)	Intrinsic Error (K) with Changing Radius
		550 km	400 km	300 km	200 km	125 km	90 km	50 km
ALP	0.40	0.150	0.148	0.140	0.131	0.124	0.120	0.108
SSC	0.06	0.105	0.104	0.101	0.101	0.101	0.100	0.099
NSC	0.51	0.088	0.083	0.079	0.075	0.069	0.067	0.058
EEU	0.05	0.168	0.167	0.167	0.168	0.168	0.167	0.160
GRE	0.31	0.201	0.199	0.193	0.180	0.165	0.162	0.154
AVG	0.27	0.143	0.140	0.136	0.131	0.125	0.123	0.116

.

For regions with intrinsic errors that were identified to be more sensitive to changes in radius values (NSC, ALP, GRE), a strong increase in intrinsic error for lower radii up to about 200 or 300 km is observed; after this range of values, the intrinsic error tends to stabilize (Figure 4). For the EEU region, the increase in the sensitivity of intrinsic errors to changes in radius values occurs between 50 km to 90 km, then stabilizes for larger region sizes. For the SSC region, the intrinsic error remains stable over the whole range of tested radius values.

4.1.2. Time Window Size

For all regions, SWC are very sensitive to the time window size. In

Table 3. Overview of the Intrinsic errors (in degree K) for each region and time window. The sensitivity index (SI) is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value (i.e., 30-day time window).

	SI (-)	Intrinsic Error (K) with Changing Time-Window
		720-day	360-day	180-day	90-day	30-day	14-day	7-day	4-day	2-day	1-day
ALP	0.80	0.129	0.125	0.124	0.119	0.108	0.096	0.086	0.075	0.061	0.043
SSC	0.87	0.119	0.115	0.114	0.109	0.099	0.090	0.076	0.067	0.042	0.033
NSC	1.00	0.080	0.079	0.077	0.070	0.058	0.052	0.048	0.037	0.029	0.022
EEU	0.77	0.178	0.178	0.179	0.177	0.160	0.141	0.118	0.092	0.062	0.056
GRE	0.78	0.175	0.173	0.174	0.167	0.154	0.141	0.121	0.100	0.073	0.055
AVG	0.85	0.136	0.134	0.134	0.129	0.116	0.104	0.090	0.074	0.054	0.042

, it can be observed that the SI for the regions vary from 0.77 in EEU up to 1.00 in NSC.

The main component of the intrinsic error accumulates within the first two weeks (Figure 5), where the average intrinsic error increases from an average of 0.042 K (1 day)) to 0.104 K (14 days).

Persistent synoptic weather systems typically remain over Europe from several days up to two weeks. Those short-term changes in the atmosphere account for main sources of SWC uncertainties.

Another significant increase in uncertainties can be observed when the time window increases from 30 to 180 days, which corresponds to increases from 0.116 K to 0.134 K on average. Based on this observation, the seasonal variability in the atmosphere seems to be significant and an important source of uncertainty.

The change in uncertainty appears to plateau when the time window size increases beyond approximately one year (Figure 5). A 721-day time window is associated with almost the same amount of intrinsic error (0.136 K) as a 180-day time window size (0.134 K).

The shortest time window that was investigated in the study corresponds to one full day; the effects of day/night cycle were not captured as a result.

4.1.3. View Zenith Angle (VZA)

We expected a rather stable behavior to be associated with changing the VZA parameter, since it is integrated in the retrieval method (Equation (1)). In particular, the method was designed to handle the whole range of possible VZA values with the same set of coefficients. However, upon further inspection of the individual intrinsic errors associated with each resultant subrange after splitting the full range of VZA values into 10 bins (Figure 6), it is evident that for VZA of more than 35 to 45 degrees, the intrinsic error increases significantly over all of the investigated regions.

Figure 7 highlights only a slight increase in the overall accuracy with respect to how the VZA range is divided into several small sub-ranges with own coefficients. Strong sensitivity to changes in the VZA is detected in the ALP site with an SI of 0.2 and the uncertainty is reduced from 0.108 K to 0.086 K (

Table 4. Overview of the Intrinsic errors (in degree K) for each region and explored number of VZA bins. The sensitivity index (SI) is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value (i.e., 1 bin).

	SI (-)	Intrinsic Error (K) with Changing VZA Bins
		1 bin	2 bins	4 bins	10 bins
ALP	0.20	0.108	0.096	0.089	0.086
SSC	0.12	0.099	0.094	0.090	0.087
NSC	0.15	0.058	0.053	0.051	0.049
EEU	0.02	0.160	0.160	0.159	0.157
GRE	0.07	0.154	0.149	0.145	0.142
AVG	0.11	0.116	0.110	0.107	0.104

). In the NSC (SI 0.15), SSC (SI 0.12), and GRE (SI 0.07) sites, the reduction in uncertainty is already very low, whereas there is no significant improvement observed over the EEU (SI 0.02) site.

It should be noted that this increase is unrelated to any confounding effects that may be attributed to pixel overlapping or blurring. While this explanation is relevant when working with pixels from real satellite images, it is not applicable with respect to simulated pixels. The latter remain perfect individual dots for the full range of VZA values. Consequently, this increase in uncertainty at larger VZA values is related to other mechanisms not considered in the split-window equation (Equation (1)).

4.1.4. Total Column of Water Vapor (TCWV)

Figure 8 and

Table 5. Overview of the Intrinsic errors (in degree K) for each region and explored number of TCWV bins. The sensitivity index (SI) is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value (1 bin).

	SI (-)	Intrinsic Error (K) with Changing TCWV Bin
		1 bin	2 bins	4 bins	10 bins
ALP	0.17	0.108	0.105	0.099	0.090
SSC	0.16	0.099	0.097	0.091	0.083
NSC	0.13	0.058	0.058	0.057	0.051
EEU	0.19	0.160	0.155	0.145	0.131
GRE	0.18	0.154	0.148	0.142	0.127
AVG	0.16	0.116	0.113	0.107	0.096

show that dividing the water vapor range into subranges with tailored coefficients has a similar effect in all regions. The sensitivity is the highest in the EEU site (SI 0.19), and it is also associated with the largest absolute reduction of error ranging from about 0.16–0.13 K. On the contrary, the lowest sensitivity (SI 0.13) and the lowest absolute reduction of error from about 0.06–0.05 K is observed over the NSC site, where the moisture content and the overall intrinsic error is also the lowest.

The sensitivity is directly related to the realistic extents of the TCWV ranges occurring in the respective regions. In this study, the TCWV range of each region is subdivided into a fixed number of bins. In the case of the NSC region, which is characterized by a low TCWC maxima, this results in narrower and more homogeneous bins that have limited impact on the overall accuracy. In contrast, the subdivision of wider regional extents of possible moisture values into smaller subranges for other locations/ sites enhances the performance.

4.1.5. Surface Temperature

Similar to the results of the investigation with TCWV, we observe that dividing the Tsfc range into subranges has a similar effect for all regions (Figure 9). In terms of absolute change in intrinsic error, the strongest reduction is observed in the EEU site, ranging from 0.160 K to 0.134 K, while the lowest reduction is observed in the NSC site, ranging from 0.058 K to 0.049 K. In terms of SI, all the regions have a similar sensitivity to Tsfc (EEU SI 0.17 to SSC SI 0.15), excepting the GRE site (SI 0.12), which is associated with a considerably lower sensitivity (

Table 6. Overview of the Intrinsic errors (in degree K) for each region and explored number of surface temperature bins. The sensitivity index (SI) is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value (1 bin).

	SI (-)	Intrinsic Error (K) with Changing Tsfc Bins
		1 bin	2 bins	4 bins	10 bins
ALP	0.16	0.108	0.101	0.097	0.090
SSC	0.15	0.099	0.093	0.089	0.084
NSC	0.16	0.058	0.055	0.052	0.049
EEU	0.17	0.160	0.150	0.144	0.134
GRE	0.12	0.154	0.147	0.143	0.135
AVG	0.15	0.116	0.109	0.105	0.099

). The observation over the latter may be related to the elevated TCWV rates around the warm Mediterranean Sea, which corresponds to the high general uncertainty related to the potential effects of Tsfc bins. However, the exact cause for this remains unknown.

4.1.6. Time of the Day

The effect of using separated daytime and night-time SWC, instead of a general SWC, is rather low across all regions. The sensitivity is highest in the ALP and EEU sites, both with an SI of 0.11, and lowest in the GRE and SSC sites, both with an SI of 0.08 (

Table 7. Overview of the Intrinsic errors (in degree K) for each region and for the scenarios with and without separated day and night-time coefficients. The sensitivity index (SI) is defined as the difference between the largest and the smallest intrinsic error, scaled to the baseline value (without day/night separation).

	SI (-)	Intrinsic Error (K) Day/Night Separation
		No	Yes
ALP	0.11	0.108	0.096
SSC	0.08	0.099	0.091
NSC	0.10	0.058	0.052
EEU	0.11	0.160	0.143
GRE	0.08	0.154	0.142
AVG	0.10	0.116	0.105

). The highest absolute reduction in intrinsic error is to be found in the EEU region (0.160 K to 0.143 K), whereas the lowest absolute reduction is to be found in the NSC region (0.058–0.052 K).

This result was unexpected and in contradiction to other studies (e.g., [13,19]). A possible explanation for this may be attributed to the application of a skin-to-bulk conversion that is implicit to the SWC in the other studies. In this study, only the atmospheric attenuation between the earth’s surface and the top of atmosphere was considered to generate the SWC. The study highlights this difference; while differentiating between day- and night-time situations makes sense for skin-to-bulk conversion, but it has a negligible effect on the correction of atmospheric attenuation of TIR radiation.

4.1.7. Overview Per Region

When comparing the impact of the different tested parameters, the order of importance differs slightly from region to region (Figure 10). However, in all regions, the SWC are most sensitive to the time window size (average SI of 0.85). Thus, overall uncertainty can be notably minimized with the reduction of the time window size.

The region size was identified to be the second most important parameter, associated with an average SI of 0.27. However, the sensitivity to the spatial extent of a region depends strongly on the region’s characteristics (e.g., topography and climatic zones). For the regions of SSC (SI 0.06) and EEU (0.05), the size of the region has almost no significance on the SWCs’ performance, whereas for the regions of NSC (SI 0.51) and ALP (SI 0.40), this parameter has a very significant effect.

Tailored SWC to subranges of VZA, TCWC and Tsfc perform slightly better than coefficients covering the whole range of these parameters. Nevertheless, the sensitivity of SWC to VZA (average SI 0.11), TCWV (SI 0.16) and Tsfc (SI 0.15) is generally relatively moderate compared to observed effects of the time window and the spatial region sizes.

The lowest sensitivity was observed for the separation into day and night coefficients (average SI 0.10). The variability between averaged day- and night-time atmospheres is less than the variability of the atmosphere in space and time. In the end, there is still a detectable improvement in all regions when differentiating between day- and night-time situations, but the effect is almost insignificant compared to the effects of the other parameters.

4.2. Validation of SWC with In-Situ Data

Different sets of SWC were used to generate LSWT time series from NOAA-17 data. The SWC are subject to changes in the following parameters: time window sizes of 14, 30, and an infinite number of days (inf.), spatial extents of 50, 200, and 400 km, once with and once without day night separation (dn1 and dn0). Each of these coefficients are applied to the same set of satellite data, and validation is performed with the same in-situ data.

The intrinsic error from these validation coefficients are shown in

Table 8. Intrinsic error of the SWC which were used for validation at Lake Geneva (EPFL) and at Lake Constance (Lindau). The values in the table represent the amount of BIAS ± SD. The columns contain the values for each station and for the three radii (50 km, 200 km, and 400 km) used to generate the SWCs. The lines contain the three time-window sizes (14 days, 30 days, and infinite) used to generate of the SWCs, once without (dn0) and once with (dn1) individual day and night coefficients.

			EPFL, Lake Geneva			Lindau, Lake Constance
			Radius (km)			Radius (km)
			50	200	400	50	200	400
Time Window (days)	dn0	14	0.01 ± 0.09	0.01 ± 0.12	0.01 ± 0.13	0.01 ± 0.08	0.01 ± 0.11	0.01 ± 0.13
		30	0.01 ± 0.10	0.01 ± 0.13	0.00 ± 0.14	0.00 ± 0.09	0.01 ± 0.12	0.00 ± 0.13
		inf.	0.00 ± 0.12	0.01 ± 0.15	0.00 ± 0.16	0.01 ± 0.10	0.01 ± 0.14	0.00 ± 0.16
	dn1	14	0.01 ± 0.08	0.01 ± 0.11	0.01 ± 0.13	0.00 ± 0.07	0.01 ± 0.11	0.01 ± 0.12
		30	0.01 ± 0.09	0.01 ± 0.12	0.01 ± 0.14	0.01 ± 0.07	0.01 ± 0.11	0.00 ± 0.13
		inf.	0.00 ± 0.12	0.00 ± 0.15	0.00 ± 0.16	0.01 ± 0.10	0.00 ± 0.14	0.00 ± 0.15

. The intrinsic errors are comparable to those observed during the sensitivity analysis for the ALP region. The lowest intrinsic error is observed for the most customized coefficients (14 days, 50 km and dn1), whereas the highest intrinsic error is observed for the most universal coefficients (inf., 400 km, dn0).

Examining the performance of the coefficients generated from the validation with in-situ data (

Table 9. LSWT validation against in-situ data from Lake Geneva (EPFL) and from Lake Constance (Lindau). The values in the table represent the BIAS ± SD of the LSWT product. The columns contain the values for each station and for the three radii (50 km, 200 km, and 400 km) used to generate the SWC’s. The lines contain the three time-window sizes (14 days, 30 days, and infinite) used to generate the SWC’s, once without (dn0) and once with (dn1) individual day and night coefficients.

			EPFL, Lake Geneva			Lindau, Lake Constance
			Radius (km)			Radius (km)
			50	200	400	50	200	400
Time Window (days)	dn0	14	−0.10 ± 1.28	−0.12 ± 1.29	−0.16 ± 1.29	0.37 ± 1.37	0.28 ± 1.39	0.25 ± 1.38
		30	−0.10 ± 1.27	−0.14 ± 1.29	−0.17 ± 1.29	0.36 ± 1.36	0.27 ± 1.38	0.23 ± 1.38
		inf.	−0.18 ± 1.24	−0.23 ± 1.24	−0.26 ± 1.24	0.31 ± 1.36	0.21 ± 1.37	0.15 ± 1.36
	dn1	14	−0.02 ± 1.32	−0.07 ± 1.31	−0.14 ± 1.29	0.56 ± 1.49	0.36 ± 1.42	0.30 ± 1.41
		30	0.01 ± 1.31	−0.07 ± 1.30	−0.14 ± 1.29	0.57 ± 1.47	0.36 ± 1.43	0.30 ± 1.41
		inf.	−0.04 ± 1.28	−0.12 ± 1.28	−0.20 ± 1.26	0.51 ± 1.46	0.33 ± 1.42	0.26 ± 1.41

), the spread (variance) is observed to be approximately one order of magnitude higher than the intrinsic error of the coefficients. For Lake Geneva, the best results in terms of bias is associated with coefficients with a higher level of specialization (EPFL: 30 days, 50 km, dn1), whereas the variance is the lowest for longer time-windows and without individual day and night coefficients (EPFL: inf., dn0). At Lake Constance, the lowest bias is associated with coefficients with a lowest level of specialization (Lindau: inf., 400 km, dn0), whereas differences in the variance are not significant. However, the variance is found to be generally lower for sets of coefficients without individual day and night coefficients (Lindau, dn0).

4.3. Uncertainty Propagation Analysis

The total uncertainty of a LSWT product was estimated using the error propagation model described in Equation (2). The application is based on the validation results described in the previous chapter with SWC uncertainties of ${\mathsf{\sigma }}_{SWC}=\left[0.07\mathrm{K},0.16\mathrm{K}\right]$ (Table 8). The choice of SWC has an influence of about 0.5% to 0.7% compared to the total uncertainty (${\mathsf{\sigma }}_{tot}=\left[1.24\mathrm{K},1.49\mathrm{K}\right]$ Table 9).

To generalize the results, the model was applied to two extreme cases to evaluate the intrinsic uncertainty associated with SWCs revealed during the sensitivity analysis (${\mathsf{\sigma }}_{SWC}=0.05\mathrm{K}$ and ${\mathsf{\sigma }}_{SWC}=0.2\mathrm{K}$), and for a range of auxiliary uncertainties (${\mathsf{\sigma }}_{aux}=\left[0.0\mathrm{K},2.0\mathrm{K}\right])$.

In Figure 11, the curves representing total uncertainty computed with ${\mathsf{\sigma }}_{SWC}=0.05\mathrm{K}$ and ${\mathsf{\sigma }}_{SWC}=0.2\mathrm{K}$ converge towards each other as auxiliary uncertainty increases. The gray curves illustrated in Figure 11 and Figure 12 represent the influence of the SWC’s accuracy on the total uncertainty ($1-{\mathsf{\sigma }}_{tot0.05\mathrm{K}}/{\mathsf{\sigma }}_{tot0.2\mathrm{K}}$); the percentage of potential uncertainty reduction when using SWC with ${\mathsf{\sigma }}_{SWC}=0.05\mathrm{K}$ instead of ${\mathsf{\sigma }}_{SWC}=0.2\mathrm{K}$ is given.

Based on this observation, the influence of SWC can be considered to be negligible for total uncertainties above 0.8 K (<3%). It becomes significant at an uncertainty of around 0.6 K (>5%). The increasing uncertainty steepens with respect to the introduction of important influences at 0.45 K (9.7%) or even at 0.3 K (23.6%).

Validation results from other studies (i.e., red triangles in Figure 12) are also included to provide an estimate and a point of reference to compare the influence of SWCs’ accuracy on the aggregated uncertainty of LSWT products from different sensors. It should be emphasized that the influence of SWC values are estimated based on a simplified error propagation model. The real SWC influence depends on the exact composition and the nature of auxiliary uncertainties, which are only considered with a black box approach in this study.

5. Discussion

The sensitivity analysis revealed that the most sensitive parameter that influences the SWC’s intrinsic uncertainty is the size of the time window during which coefficients are valid. The largest accumulation of intrinsic error was observed with the increase of the time window size from one day to around two weeks. Thus, a major part of the SWC’s uncertainty is related to synoptic scale weather variability. However, the regression of coefficients with time window sizes below two weeks leads to strong variations within the SWC over time, and their long-term consistency is questionable. The second important source of increase in SWC intrinsic error is observed when the time window changes from monthly to yearly time periods. This indicates that the seasonal atmospheric variability may be another important source of uncertainty in SWC. With further increases to time window sizes beyond one year, the performance did not decrease further. This supports the assumption made by Hulley et al. 2011 [13], which claims that if each possible atmospheric configuration at a specific location is covered within a one year period, the coefficients are valid for the whole defined study period.

The local SWCs tend to perform better than generalized ones when considering the effect of variations in spatial extent. However, the difference is not as distinct as expected, particularly with regards to the results of lake-specific LSWT retrievals from the literature [11,13,19,37]. The impact of the spatial extent depends strongly on the topography, land cover variability, especially the differences between land and sea surfaces nearby, and the climatic characteristics of the region. In topographically more homogeneous areas such as the EEU or SSC regions, the spatial extent of the SWC’s applicability is of low significance to the SWC performance. Even SWCs applicable for spatial extents above 500 km perform similarly to very local SWC (<100 km). However, in heterogeneous regions (e.g., GRE), SWC perform significantly better when customized to specific local conditions. This observation agrees with the results from [9], which emphasizes the regional topographic and climatic effects on LSWT uncertainty.

The VZA contributes to a significant increase in the SWC’s intrinsic error, particularly at high viewing angles around 45–60 degrees. The increased uncertainty is not related to pixel overlapping or blurring. It is an indication that the parametrization of the VZA in the split-window equation (Equation (1)) is not optimal (see Section 4.1 VZA). However, the potential for improvements seems very limited even if there was a better mathematical expression describing the integration of VZA in the split-window retrieval approach. In fact, during LSWT retrieval, a potentially small performance gain using tailored SWC would likely be concealed by the combined effects of other sources of uncertainties that also increase with elevated VZA values (e.g., pixel overlapping and blurring). This result is also in agreement with the fact that retrieval methods, which do not directly account for the VZA [37,39] yield results with similar performances to studies that do [19,27].

Newman et al. [34] mention that the temperature-dependent emissivity is often underestimated and its effect neglected as a result. Nevertheless, differentiated SWC for ranges of surface temperatures are only associated with moderate improvements, even though temperature dependent emissivity of the surface is not considered within the split-window equation (Equation (1)).

Brown and Minnet [28] used separated SWC for different water vapor rates to improve their results. In this study, differentiating coefficients for specific ranges of water vapor content only had a moderate effect on the performance of SWC.

The use of differentiated coefficients for day- and night-time retrieval did not result in a significant reduction in intrinsic errors compared to the use of coefficients derived under general conditions. At first sight, this contradicts with findings from different studies (e.g., [13,19]) that reported improvements when using separated sets of SWC for day- and night-time temperature retrievals. The idea to differentiate between day- and night-time retrievals has its origins in the SST retrieval methods, where the SWCs are determined from matchup data with bulk temperature measurements from buoys. Therefore, a skin-to-bulk conversion, which corrects for the thermal skin effect, is implicitly included into the coefficients. In the case of the use of synthetic matchup data from radiative transfer modelling, as used within this study, only contributions of atmospheric attenuation between skin temperature at the earth’s surface and brightness temperature at the TOA is considered in the derived SWC. Comparing the results reported in Riffler et al. [19] and the study results, the separation into day-time and night-time data is applicable for skin-to-bulk conversion, but is not suited for atmospheric correction. In fact, the temperature difference between skin and bulk of a water body is highly responsive to sun irradiation and stratification of the lake, which differs between day and night.

The validation with 4 years (2004–2007) of NOAA-17 data shows that the use of different tailored SWCs had no significant effect on the retrieval accuracy. At Lake Geneva, the SWCs with the highest degree of specialization, perform slightly better than the coefficients with the lowest specialization, whereas the contrary is true in the case of Lake Constance. Nevertheless, the impact of the SWC are considered to be negligible based on the validation results. It should be noted that skin-to-bulk correction was not applied to the validation, thus, the LSWT skin temperature derived from satellites is directly compared to in-situ bulk measurements.

The theoretical influence of SWC on the aggregated uncertainty associated with the final LSWT product could be estimated with the error propagation model. The validation results of the impact of the SWC where estimated to be neglectable (0.5–0.7%) which confirm the result from the validation. However, by generalizing the relation between the SWC’s uncertainty and the product uncertainty, it was demonstrated that the importance of customized SWCs increases with increasing accuracy of the LSWT product. It was estimated that customized SWC start to have a significant influence (>4.8%) when the total aggregated uncertainty of the LSWT product is <0.6 K.

6. Conclusions

Tailoring the split window coefficients to certain atmospheric conditions or geographical locations generally increased the accuracy associated with the split window retrieval method. However, during validation with in-situ measurements, the subtle performance differences of the tested split window coefficients (SWC) could not be linked to the accuracy associated with the final lake surface water temperature (LSWT) product. Other cumulative sources of uncertainty within the processing chain were likely dominant (e.g., calibration, cloud contamination, georectification uncertainty, skin to bulk temperature conversion etc.). It was shown that with improvements to the overall accuracy of the retrieval process, the tailoring of SWC becomes more important (Figure 11). As soon as LSWT products are required to reach accuracy targets below ~0.6 K, the tailoring of SWCs becomes a significant factor (influence >5% relative to the total uncertainty) to reach the target.

The study compared the effectiveness of certain common approaches to generate SWC. For the first time, the potential gain in the performance of optimized SWC was isolated from the overall processing chain. Some common assumptions for SWC generation could be confirmed, whereas others require further evaluation:

In general, we can assume that a set of coefficients regressed with one year of empirical data can be considered to be valid for all the other years as well, with the exception of some extraordinary changes in the atmosphere e.g., due to volcanic eruptions. We could also conclude that defining the degree of SWC localization or regionalization based on defining the radius of a circular region is not an optimal approach.

Other characteristics such as altitude, latitude, average humidity, or location relative to the directionality of a mountain ridge, all can have more influence on the results than based on the consideration of the absolute distance between points alone. The use of a single set of coefficients to cover the whole range of view zenith angle (VZA), in combination with a VZA threshold of 45° for the data, is a reasonable trade-off between accuracy and the number of omitted data points per satellite overpass. For total column of water vapor (TCWV) and surface temperature (Tsfc), the performance gain when using differentiated coefficients for ranges of TCWV and Tsfc is modest compared to the increase in complexity.

The day–night separation of SWCs had a very low impact on the SWC accuracy. This is because potential differences between day- and night-time retrieval is less related to variations in atmospheric absorption of thermal infrared radiation (TIR) than to heat exchange processes inside the surface water layers and at the interface to the atmospheric boundary layer. Thus, it was also concluded that the SWC should only account for the atmospheric correction of the TIR signal. The heat transfer between the lakes’ skin and bulk layers is governed by different physical mechanisms, and should be tackled outside the SWC. While the separation between the two processes is difficult to achieve when the SWCs are derived from matchup data based on bulk measurements, it is feasible with an RT modelling approach designed to derive SWCs

Finally, the validation showed that the benefits of tailored SWC are of increased relevance when other uncertainties within the processing chain are minimized. Otherwise, the application of generalized SWCs does not adversely affect the overall retrieval quality, and can be a reasonable choice.