Using 3D Point Clouds Derived from UAV RGB Imagery to Describe Vineyard 3D Macro-Structure

Abstract

In the context of precision viticulture, remote sensing in the optical domain offers a potential way to map crop structure characteristics, such as vegetation cover fraction, row orientation or leaf area index, that are later used in decision support tools. A method based on the RGB color model imagery acquired with an unmanned aerial vehicle (UAV) is proposed to describe the vineyard 3D macro-structure. The dense point cloud is first extracted from the overlapping RGB images acquired over the vineyard using the Structure from Motion algorithm implemented in the Agisoft PhotoScan software. Then, the terrain altitude extracted from the dense point cloud is used to get the 2D distribution of height of the vineyard. By applying a threshold on the height, the rows are separated from the row spacing. Row height, width and spacing are then estimated as well as the vineyard cover fraction and the percentage of missing segments along the rows. Results are compared with ground measurements with root mean square error (RMSE) = 9.8 cm for row height, RMSE = 8.7 cm for row width and RMSE = 7 cm for row spacing. The row width, cover fraction, as well as the percentage of missing row segments, appear to be sensitive to the quality of the dense point cloud. Optimal flight configuration and camera setting are therefore mandatory to access these characteristics with a good accuracy.

1. Introduction

Grapevine productivity depends on physical, biological and chemical factors, including climate, soil characteristics, grape variety, topography, occurrence of pests or diseases and management practices. Spatial variations of these factors within fields and between fields impact grape quality and yield. An optimal management of cultural practices during the growing season and at harvesting must therefore be taken into account. In this context of precision viticulture, which began in 2000 as reviewed by [1], remote sensing in the optical domain offers a potential way to extract spatial information on the crop state in a non-destructive way. It can later be used in decision support tools.

Although potentially promising, remote sensing from satellite observations is not often routinely used except by [2], who characterize crop coefficients for irrigation management. Indeed, satellite observations raise a number of problems specific to vineyards, mainly associated with the heterogeneous structure of the canopy in relation to the spatial resolution of the satellite images. First, the spatial resolution of the existing sensors providing images at a reasonable cost, such as LANDSAT, SPOT or Sentinel-2 (from 5 to 30 m), is not adapted to very small vineyard fields [3]. The main limitation in this case is due to the mixed nature of the signal measured in a single pixel [4] since vineyards are cultivated in rows with the row spacing potentially occupied by green grass, making the extraction of the specific signature of the rows complex. Further, the row structure [5,6,7], as well as the terrain slope [8,9], induce directional effects on the reflectance signal that must be accounted for. The use of higher spatial resolution systems (a few centimeters to a few decimeters) thus appears mandatory to identify rows and extract the corresponding characteristics while minimizing the effects of the inter-row status (bare soil, senescent or green grass) and row orientation. Further, the row structure is of prime importance for the processing and interpretation of other sources of remote sensing data such as (i) thermal infrared images to identify shadowed elements when evaluating evapotranspiration for water stress monitoring [10] or (ii) visible/near infrared images to accurately compute the fraction of intercepted radiation [11].

When considering satellite sensors, the acquisition date is dependent on the orbital characteristics of the platform and on cloud occurrence. Conversely, it is much more flexible with airborne or unmanned aerial vehicle (UAV) platforms, even if the acquisition also depends on climatic conditions (wind, rain) and legal constraints. This allows planning flights at a date very close to specific phenological stages for the detection of plant stress and diseases or for pre-harvest characterization [12].

A number of studies explored aerial imagery with resolutions of around few decimeters to map crop vigor [3,13,14,15] and grape quality [16]. Most of them are based on the normalized vegetation index (NDVI) proposed by [17]. As an alternative, Zarco-Tejada et al. [5] proposed developing a radiative transfer model inversion technique to estimate some state variables of the vineyards. They used airborne hyperspectral measurements aggregated at a spatial resolution of a few meters to estimate the leaf area index and the leaf chlorophyll content of vineyards with bare row spacing.

The emergence of UAVs in recent years has thus provided new opportunities to obtain timely high spatial resolution images over vineyards at a reasonable cost. However, a recent review of UAV acquisitions applied to vegetated areas [18] indicates that the objective of most of the published studies focus on UAV vegetation characteristics mapping, while only a few actually present quantitative validation results where UAV estimates are compared to ground measurements. Many of these studies are based on the use of multi or hyperspectral data to compute several vegetation indices in relation to the vegetation vigor [16,19,20,21,22] or grapevine species [23,24]. More quantitative studies are related to water and nitrogen stress [21,25]. Some authors have also investigated the combination of spectral domains such as the optical and thermal infrared ones [25,26].

One of the main issues in vineyard characterization is to isolate the pixels belonging to the rows from the ones belonging to the row spacing. The difference in spectral properties between rows and inter-rows were first exploited by applying a threshold on vegetation indices computed on multispectral images [3,22,27]. Other studies, based both on the spatial and the spectral properties of the rows, applied a Fourier transform to the red band of RGB images [28,29,30]. However, these methods are obviously dependent on the spectral contrast between the row and inter-row composition with degraded performances in the presence of grass.

To overcome this problem, another solution is to take advantage of the multiplicity of images acquired by the UAV over the surface. The large fraction of overlapping between them is capitalized by deriving a dense point cloud (DPC) using photogrammetric techniques such as Structure from Motion algorithms (SfM, [26,31,32,33,34]). The DPC is then used to derive the digital surface model (DSM) after filtering and meshing. This was successfully applied to major crops [32], as well as recently to vineyards [35]. In this study, the DPC was used to compute the vegetation cover fraction, which was then related to the leaf area index. However, the information provided by the DPC is much richer and potentially allows characterizing the full 3D macro-structure of the canopy, e.g., the envelope of each row.

The objective of this study is to develop an algorithm for vineyard structural characteristic estimation from dense point clouds derived from the RGB color model images acquired with an UAV. It is achieved in the context of the Piemonte area in northeastern Italy which is composed of small fields of around 1 ha, frequently located on steep slopes. Green grass is often present within the row spacing. The experimental site, the ground measurements as well as the UAV acquisitions are first presented. Then, the methods used to obtain the DPC and to extract the canopy architecture characteristics are described. The results are finally presented, focusing on four main characteristics of the macro-structure of the canopy, i.e., row orientation, height, width and spacing.

2. Materials and Methods

2.1. Experimental Site

The experiment took place in the Fontanafredda vineyards, famous for the Barolo red wine (Italy, 44.64°N, 7.98°E), on 12 September 2013 under sunny clear sky conditions. The area is characterized by a hilly topography, with mainly vineyard plots. The rows are generally oriented along iso-altitude curves. The row spacing is variable with grass growing in between rows in most of the cases and cut several times during the season. The canopies are pruned to control the amount of vegetation and ease the maturation of the grapes, but shoots are often growing after the pruning operation.

There were 20 sampled sites called elementary sampling units (ESU) (Figure 1). They cover a square area of 10 m side and were selected to represent the range of possible growing patterns, row orientation and slopes as well as variable amount of grass between the rows. The coordinates of each ESU were measured with a GPS within a few meters accuracy. The 20 ESUs were grouped into four zones corresponding to four UAV flights (Figure 1). The variation in height in each area covered by the flights is 2 m (flight 3), 14 m (flight 1), 20 m (flight 2) and 35 m (flight 4).

2.2. Ground Measurements of the Row Characteristics

For each ESU, the height, width and distance between rows were measured at the ground level using a ruler (Figure 2). Measurements were averaged over ten replicates along two adjacent rows in the center of the ESU. The maximum height corresponds to the distance between the soil and the top of the highest leaf. When the row section was similar to a rectangle, the row width was measured at about 120 cm from the soil. For more complex patterns (trapezoidal), we measured the row width at the height corresponding to the maximum row width. As for the height measurements, we calculated the average over ten replicates acquired along two adjacent rows. Finally, the row spacing (distance between trunks across the row direction) was measured with only four replicates since plants were regularly spaced within the crop. We then approximated the measured vegetation cover fraction of each ESU as the ratio between the row width and the row spacing. The accuracy of a single dimension measurement was about 3 cm, and the standard deviation across the replicates was around 10 cm for the height, 5 cm for the width and 3 cm for the row spacing.

2.3. Unmanned Aerial Vehicle (UAV) Measurements

UAV measurements were performed and processed to generate the DPC by the AIRINOV private company. They used a 2 m wingspan fixed-wings UAV built in EPP (Expanded PolyPropylene). It weighed less than 2 kg including the payload. This allows hand-launching for take-off and direct landing on the plane belly. The UAV is battery-powered, and can fly up to 50 min at about 50 km/h speed at altitudes ranging from 20 m to 300 m. It can scan a 15 ha area in about 10 min. Real-time UAV positioning was monitored by a GPS with an accuracy of a few meters with regards to the flight plan, mainly due to aerologic conditions and, to a minor extent, GPS position inaccuracies. The height of the plane was monitored by barometers.

A Panasonic digital RGB camera DMC-GF3 was mounted on the UAV. It is characterized by a 17.3 mm ×13.0 mm sensor matrix of 12 million pixels, and a focal length of 14 mm. The images were recorded on a flash card. Priority was given to the speed, leading to exposure times lower than a few milliseconds. The images were acquired at a frequency of 1 Hz, allowing about 60% to 80% overlapping along and between the tracks, according to the nominal 45 km/h UAV speed.

The UAV flew in straight South−North-oriented parallel lines. The nominal flight altitude relative to the take-off point was computed to provide a Ground Sampling Distance (GSD) between 2 and 6 cm for each ESU (

Table 1. Characteristics of the four zones corresponding to the four flights.

Flight Number	1	2	3	4
Sampled ESUs	1–4	5–9	10–11	12–20
Surface of the flown area (ha)	2.5	4.4	3.5	9.3
Flying Height 1 (m)	89	89	202	71
GSD 2 (cm)	2.8	2.8	6.4	2.2
Images (Nb/ha)	81	36	15	33
Tie points 3 (Nb/m2)	2.5	2.8	6.7	2.7

¹ The flying height is the vertical distance between the take-off point and the UAV. ² GSD is the Ground Sampling Distance. ³ The sparse point cloud density is quantified by the number (Nb) of tie points per m².

). However, because of the complex topography of the area, the distance between the UAV and the surface was variable. This induced significant variations in GSD (from 2 cm up to 7 cm), as well as in the nominal overlapping along and across tracks (Table 1). As a consequence, more than nine overlapping images were available for almost all the ESUs, except for ESU#8 (4 images), ESU#20 (6 images) ESU#18 (7 images) and ESU#19 (8 images), which were observed from a shorter distance. The density of images (Nb. Images/ha, Table 1) for each flight also varied significantly because of variations in flight height.

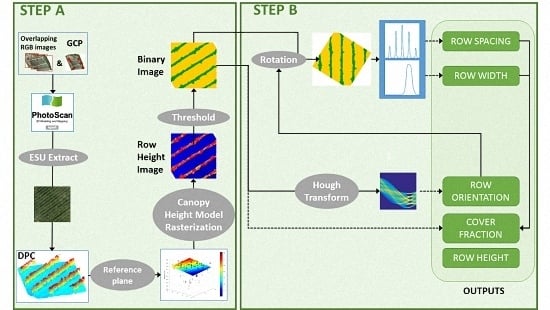
2.4. Characterizing the Row Macro-Structure: Algorithm Overview

Figure 3 presents an overview of the algorithm that computes the characteristics of the 3D macro-structure of the rows. The pre-processing step consists in deriving a binary image from the overlapping RGB images acquired with the UAV (Figure 3, Step A). This is achieved by generating the dense point cloud (DPC) with the Agisoft PhotoScan software (Version 1.1.0) and then gridding the whole image into 10 m × 10 m square cells. Then, for each cell, we separate the soil pixels from the ones corresponding to the vegetation by fitting a soil reference plane using the 10% lowest points. This allows deriving the Canopy Height Model (CHM), e.g., the altitude of the points relating to the soil within the cell. The DPC is then rasterized with a 5 cm resolution and transformed into a binary image where background and vineyard are separated. Step B consists of characterizing the macro-structure of the vineyard rows (Figure 3, Step B). First, row height is derived from the height image. The orientation of the rows is computed by applying a Hough transform of the binary image, which is then rotated accordingly to get vertically oriented rows in the image. The cumulated profile of horizontally oriented vegetation pixels is finally computed to estimate row width and row spacing. Different methods are also used to estimate the vineyard cover fraction.

3. Fine-Tuning the Pre-Processing of Images (Step A)

This section describes the pre-processing steps (Figure 3, Step A) that require adjusting thresholds and parameters.

3.1. Point Cloud Derived from Overlapping RGB Images

The widely used Agisoft PhotoScan software [36] was run by AIRINOV to generate the DPC from overlapping RGB images acquired with the UAV. PhotoScan was selected according to [37] and [38], who demonstrated that it provides the most reliable results among existing softwares based on Structure from Motion algorithms. For each flight, between 5 to 12 ground control points (GCP) were identified on the Google Earth image (Figure 1) and used in PhotoScan to get the absolute coordinates of the DPC. The accuracy of the geometric calibration over the GCP is between 2 to 3 m.

The PhotoScan software automatically adjusts the distortion characteristics of the camera (three radial and two2 tangential distortion coefficients) and aligns the overlapping images using a SIFT (Scale Invariant Feature Transform) algorithm that detects key points which correspond to specific features in the images [39]. Finally, the key points matching between overlapping images, called tie points in PhotoScan, are used to determine the pairs of overlapping images and compute the camera positions. Tie points constitute the sparse point cloud which is later used to generate the DPC [40]. The average density of tie points varies significantly between 2.5 to 6.7 tie points/m² depending on the flight: higher altitudes provide more overlap between images and increase the density of tie points despite the decrease of GSD (Table 1). All these computations are applied over each ESU, e.g., 10 m square cells corresponding to the elementary grid used in this study. The density of the PC varies also significantly as a function of the GSD of the images (Figure 4) between around 100,000 points/m² for the lowest ground sampling distance (Flight 3, ESU#10 and ESU#11) up to 700,000 points/m² for the highest one (ESU#19). It was not possible to extract a DPC for ESU#5 because of the insufficient number of overlapping images.

3.2. Deriving the Crop Height Model (CHM)

For each cell, the altitude of the background is assumed to be a tilted plane. The cell is first decomposed into a set of sub-blocks. Due to a relatively large row spacing in the Piemonte area vineyards, the cover fraction should be smaller than 90%. Under this assumption, by considering 2 × 2 m² sub-blocks, the 10% points of the DPC with the lowest altitude belong to the background. Indeed, the sub-block side length (2 m) is slightly larger than the expected row spacing. Further analysis (not shown for the sake of brevity) confirmed that this 10% threshold is efficient to identify the background altitude.

The reference plane is fitted to the 10% lowest points over the 25 sub-blocks. We used a robust fitting technique [41] to limit the influence of possible outliers. As shown by Figure 5, ESU2 presents more outliers than ESU19. This is due to the fact that the camera positioning is better estimated for ESU19 since the point cloud density is much higher.

Once the reference plane is estimated, we build the CHM by computing the relative height of each DPC point in the grid cell as the difference between its altitude and the one of its vertical projection on the reference plane. The height of the points that are lower than the reference plane is set to 0. This algorithm does not consider a spatial continuity constraint of the reference plane between two adjacent 2 × 2 m² sub-blocks. However, results show that the discontinuities are marginal due to both the use of the robust fitting technique and the limited local variations of the terrain slope and aspects in that area. Finally, when the row spacing is covered by grass, the reference plane altitude might be slightly overestimated, which could lead to possible row height underestimation.

3.3. Dense Point Cloud Rasterization

The macro-structure of the canopy is described using a regular fine grid. Each cell of this fine grid is referred to a pixel in the following. The local height of the macro-structure is computed as the maximum height of the DPC points included in each pixel. The size of the pixel should thus be large enough to contain a sufficient number of DPC points and must be smaller than a leaf, e.g., around few cm². Two pixel sizes were tested: 2 cm and 5 cm. Figure 6a shows that the percentage of empty pixels (no DPC point inside) is substantial when considering a 2 cm resolution. This is especially true for ESU#10 and ESU#11 for which the ground sampling distance was degraded because of higher flying altitudes of the UAV (Table 1). Conversely, the 5 cm pixels provide a percentage of empty pixels always lower than 5% (Figure 6a).

When considering the 5 cm resolution, the number of points per pixel significantly varies depending on the density of the DPC (Figure 6b). This latter is primarily controlled by the ground sampling distance of the original images. There are generally 5 to 10 DPC points in each pixel, except for ESU#10 and ESU#11 because of the low GSD (Table 1). Considering the relatively sparse DPC with still a high number of empty pixels, ESU#10 and ESU#11 will not be included in the further analysis. For the other ESUs, the number of DPC points per pixel (Figure 6b) are unevenly distributed, with generally higher values on the rows, especially on their edges (Figure 7). This can be explained by the more textured nature of the rows as compared to the background. Moreover, row edges present interesting features that make them good key point candidates.

3.4. Binary Image Generation: Separating the Row from the Background

The convex-hull of the canopy, represented by the fine-gridded height map previously computed, is used to separate the vegetation from the background. A 3 × 3 pixel filter is first applied to fill isolated empty pixels: if more than 5 pixels over the surrounding eight ones are not empty, the height is computed as the median height of the available surrounding pixels. A threshold height value is then used to assign each pixel to a background. Below this threshold, the pixel is considered as background. To determine the optimal height threshold to create the binary image, the height cumulative frequency distribution in each ESU is analyzed.

Results show that the height distribution rapidly reaches a plateau after 50 cm up to around 170 cm (Figure 8a). This is explained by the parallelepipedic shape of the vine rows generated by the pruning practices in Fontanafredda. The row width is thus almost constant along the plant height which makes the method mostly sensitive to the top leaves due to the flight height and the restricted field of view of the camera. ESU#8 and ESU#19 are showing an unexpected behavior with around 98% of the pixels with a height lower than 50 cm. As a matter of fact, for these ESUs, the point density within the DPC is low, and null along the rows while an average value of 9 (ESU#8) and 19 points (ESU#19) is observed (Figure 6) despite the low number of images acquired for these ESUs (Section 2.3). This shows that the spatial distribution of empty cells in the DPC may strongly impact the results. We thus discarded ESU#8 and ESU#19 for further analysis and we strongly recommend to perform a first visual check of the DPC such as proposed in Figure 7 before processing the data. The influence of the threshold value within the 50–170 cm range on the percentage of vegetated pixels is shown in Figure 8b. Results show that the sensitivity to the threshold value is low (standard deviation between 0.1% and 2%) due to the parallelepipedic shape of the rows. The threshold value is consequently set to 50 cm to be consistent with the minimum height observed on the ground (see lower points in Figure 8a). Then, the image over each ESU is classified accordingly into vine or background (or empty pixels) using the 50 cm height threshold value to generate a binary image. A closing morphological operation is eventually applied to remove outliers corresponding to pixels surrounded by pixels belonging to the other class.

4. Estimation of Vineyard Row Characteristics (Step B)

The binary images and corresponding gridded height images obtained after the preprocessing step A are processed to derive the row characteristics and compare them to ground level measurements.

4.1. Row Height

Defining row height is difficult since the top of the row is not flat and uniform along the row as shown by Figure 2. We therefore propose to define the row height according to the distribution of the elevation of the pixels in each ESU. The empirical cumulated distribution function of pixel elevation is first computed from the gridded height image (Figure 9a). Then, we select the cumulated frequency ($F_{Height}=0.68)$ that minimizes the RMSE (root mean square error) between the corresponding height $\left(H_{row}\right)$ and the measured row height over all the ESUs (Figure 9b). The RMSE presents a flat minimum between $0.55<F_{Height}<0.75$. This indicates that the row height estimation is not very sensitive to $F_{Height}$ within this range. For $F_{Height}=0.68$, the RMSE is quite good (9.8 cm) when compared to the accuracy associated with the row height measurements which presents a standard deviation between 3 cm and 29 cm over the ESUs (Figure 9c).

4.2. Row Orientation

The row orientation is estimated by applying the Hough transform [42] to the binary images similarly to the work of [29]. The Hough transform is a well-known algorithm that identifies linear features in an image: each pair of vine cells in the binary image forms a line. When represented in polar coordinates, the radius (ρ) is the distance between the two vine cells and the angle (θ) corresponds to the line orientation. Linear features correspond to high occurrence of [ρ, θ] values in the [ρ, θ] feature space (Figure 10a). The orientation from the north of the linear features (i.e., the rows in our case) is given by θ. Although the row orientation was not measured on the ground, the algorithm was validated by simply rotating the binary images by θ and assessing visually how vertical the rows were. Results confirm the efficiency of the algorithm to estimate the actual row orientation as illustrated in Figure 10b,c.

4.3. Row Spacing

Once the row orientation is computed, the rotated binary image (Figure 10c) is used to compute the profile of the cumulated number of vine cells along the vertical direction, i.e., along the rows. Row center location corresponds to the peak summits of cumulated vine pixels (Figure 11a). To limit uncertainties due to relatively flat peaks, the summit location ($P_s$) is defined as the value for which the same cumulated number of pixels is observed from both sides. Further, to eliminate artefacts due to image borders, the first and last peaks are removed in case they are not fully included in the ESU. Finally, a constraint is put on the minimum distance between peaks to prevent from identifying rows that would be unrealistically spaced. A minimum distance of 35 pixels (175 cm) is used, considering that the row spacing in such vineyards is larger than 250 cm. This constraint must therefore be adapted when applied to other vineyards using different planting patterns. The row spacing is estimated as the average distance between row peaks.

Figure 11b shows a good agreement between the estimated and the measured row spacing over the 15 ESUs. The root mean square error (RMSE) between estimated and measured row spacing is 9 cm when considering all the ESUs together. However, ESU#4 shows an unexpected overestimation. For this particular ESU, a problem related to the ground measurements is suspected because of the low number of replicates (4) and the corresponding high standard deviation (16 cm). When removing ESU#4, a good accuracy of row spacing estimation is obtained (RMSE = 7 cm), considering the 5 cm resolution of the binary images.

4.4. Row Width

Once each row center is identified, the coordinates of the pixels across the row direction are shifted so that all the rows of the ESU overlap. The row cumulated profile is computed to identify the peak summit ($P_s$) and the corresponding value $CP\left(P_s\right)$ of the cumulated row profile. The row width is then defined as the distance between the two points of the cumulated profile corresponding to $T_{Width}\mathrm{x}CP\left(P_s\right)$ (Figure 12a) where $T_{Width}$ is an optimized threshold value. Similar to what is proposed for the height determination, the value of $T_{Width}$, is adjusted to provide the best agreement with the ground measurements. The RMSE shows a relatively flat minimum between $60\%<T_{Width}<75\%$ (Figure 12b). The optimal value is $T_{Width}$ = 68% corresponding to a RMSE = 8.7 cm. This shows a relatively good agreement with the observed row width values, considering the image resolution (5 cm), and the ground measurement accuracy: the standard deviation of the measurements within an ESU varies between 2 cm for ESU#13 and 8.5 cm for ESU#20 (Figure 12c). The use of the cumulated profile makes the method robust and little sensitive to missing segments along the rows (unless the whole row is missing) and to the presence of grass in the inter-row.

4.5. Cover Fraction and Percentage of Missing Row Segments

The cover fraction can be computed in two different ways: it can be estimated in the same way as the ground measurements by dividing the previously estimated row width by the row spacing using the binary images (M1). Alternatively, it can be estimated by computing the ratio of the vegetated pixels to the total number of valid pixels over the image (M2). As expected, Figure 13a shows a quite good agreement between ground measurements and UAV estimates using the same computation method (M1, RMSE = 2.6%). However, higher discrepancies are observed when counting the number of vegetated pixels (M2, RMSE = 4.2%). This can be explained by two factors: (i) invalid pixels that may correspond either to vegetation or soil can bias the results, and (ii) method M1 (also applied to ground measurements) does not take into account possible missing segments of rows.

The percentage of missing segments of rows for each ESU was therefore computed. When considering the rotated binary image (vertical rows), a missing row segment is defined as a series of horizontal lines perpendicular within the row with no vegetation pixel. Each individual row is first extracted from the image with rows oriented vertically, using the estimated position of the row center ($P_s$) and the row spacing. The profile of the sum of vegetation pixels perpendicular to the row is then computed to retrieve the number of lines with no vegetation. The percentage of missing row segments is finally computed over all the rows in the ESU as the total number of missing lines divided by the total length (in pixels) of the rows.

Results show that when the percentage of missing row segments and the percentage of missing pixels are small (ESUs 1 to 4, 13, 16, 17), a very good consistency between the two methods and the ground measurements is observed (Figure 13a). Further, for ESUs with a significant percentage of missing row segments and few invalid pixels (ESUs 6, 7, 12 and 14), the vegetation cover fraction is not accurately estimated when using the row width and row spacing, as in method M1 and ground measurements. Finally, when the percentage of invalid pixels is significant (ESUs 9, 15, 18, and 20), the consistency between the two methods for cover fraction estimation and the ability of detecting missing segments is weak: results mainly depend on whether the invalid pixels are mainly located within the row or not: for ESU#9, the cover fraction estimated with M2 is lower than that using M1 since invalid pixels are mainly located in the fourth row (Figure 13b top). Conversely, a good consistency is observed between the two methods for ESU#18 for which the invalid pixels are located consistently at the border of the rows (Figure 13b bottom). However, the good consistency does not mean that the estimated cover fraction is accurate since, in this case, the row width of ESU#18 was significantly underestimated (Figure 12).

5. Conclusions

A dedicated method was developed to estimate several vineyard characteristics using the RGB method imagery acquired from an unmanned aerial vehicle (UAV) platform. It includes row orientation, height, width and row spacing, as well as canopy cover fraction and percentage of missing row segments. Validation against ground measurements was performed when possible and showed good performances of the algorithms.

The dense point cloud (DPC) is derived from a Structure from Motion (SfM) algorithm applied to RGB images. We used the dense point cloud to separate the background from the vineyard. Conversely to methods based on classification of multispectral or RGB images, the proposed algorithm is not sensitive to the presence of grass between the rows. Further, the height threshold value used to separate the background from the vegetation might be much less sensitive to the illumination conditions as compared to the multispectral or RGB-based methods [27]. However, both the flight configuration (altitude, UAV speed, camera resolution, field of view and overlap between images) and the photogrammetric processing appear critical to provide dense point clouds of good quality with evenly distributed high density points. This study shows that when the number of RGB images over an area is not sufficient and when the ground sampling distance is too degraded, the quality of the dense point cloud is poor. Further, the point density is often lower at the row edges, resulting in a loss of accuracy of the row characteristics estimates. This particularly impacts the row width and vegetation cover fraction. A quality flag should therefore be proposed to characterize the spatial sampling in terms of number as well as location/distribution of the missing pixels in the binary image.

The algorithm we developed to compute the row height and width requires two parameters ($F_{Height}\mathrm{and}{T}_{Width})$. Because of the rectangular shape of the rows in our experiment site, the algorithm is not very sensitive to these parameters over a large range of variation. This demonstrates the robustness of the algorithms. However, in case of rows characterized by other shapes, more attention must be paid to these parameters.

The good accuracy obtained in row height, width and spacing as well as the percentage of missing row segments when the flight configuration is optimal allows computing the row volume that is one of the main inputs to estimate the fraction of light intercepted by the vineyards (FIPAR), knowing the leaf area density in the canopy volume and the leaf inclination distribution function. The combination of SfM with multispectral imagery acquired from the same UAV platform should thus provide all the information required to calculate FIPAR. Future work will therefore be dedicated to the estimation of more functional characteristics of the vineyards.