An Empirical Ocean Colour Algorithm for Estimating the Contribution of Coloured Dissolved Organic Matter in North-Central Western Adriatic Sea
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Measurements of Seawater
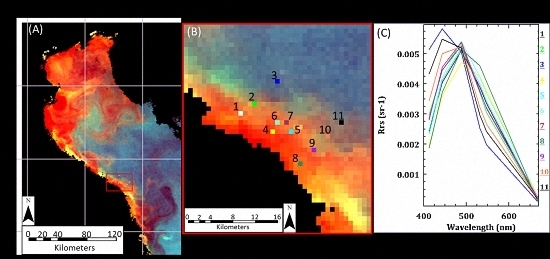
2.3. Satellite Data and Processing
2.4. CDOM Models
3. Results
3.1. Field Distribution of CDOM
3.2. Model Definition
3.2.1. Simple OLS Linear Regression
3.2.2. Dependent Variable Transformation
3.2.3. Generalized Least Squares (GLS)
3.2.4. Curvature of the Residuals
3.2.5. Model Validation
3.3. Application of Satellite-Derived CDOM
4. Discussion
5. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Volpe, G.; Santoleri, R.; Vellucci, V.; Ribera d’Alcala, M.; Marullo, S.; D’Ortenzio, F. The colour of the Mediterranean Sea: Global versus regional bio-optical algorithms evaluation and implication for satellite chlorophyll estimates. Remote Sens. Environ. 2007, 107, 625–638. [Google Scholar] [CrossRef]
- McClain, C.R. A decade of satellite ocean color observation. Annu. Rev. Mar. Sci. 2009, 1, 19–42. [Google Scholar] [CrossRef] [PubMed]
- Del Vecchio, R.; Subramaniam, A. Influence of the Amazon River on the surface optical properties of the western tropical North Atlantic Ocean. J. Geophys. Res. 2004, 109, C11001. [Google Scholar] [CrossRef]
- Pan, X.; Mannino, A.; Russ, M.E.; Hooker, S.B. Remote sensing of the absorption coefficients and chlorophyll a concentration in the U.S. southern Middle Atlantic Bight from SeaWiFS and MODIS-Aqua. J. Geophys. Res. 2008, 113, C11022. [Google Scholar] [CrossRef]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Hansell, D.A.; Lorenzi-Kayser, M. Global distribution and dynamics of colored dissolved and detrital organic materials. J. Geophys. Res. 2002, 107, C123228. [Google Scholar] [CrossRef]
- Keith, D.J.; Yoder, J.A.; Freeman, S.A. Spatial and temporal distribution of coloured dissolved organic matter (CDOM) in Narragansett Bay, Rhode Island: Implication for phytoplankton in coastal waters. Estuar. Coast. Shelf Sci. 2002, 55, 705–717. [Google Scholar] [CrossRef]
- McKee, D.; Cunningham, A.; Jones, K.J. Optical and hydrographic consequences of freshwater run-off during spring phytoplankton growth in a Scottish fjord. J. Plankton Res. 2002, 24, 1163–1171. [Google Scholar] [CrossRef]
- Bricaud, A.; Morel, A.; Prieur, L. Absorption by dissolved organic matter of the sea (yellow substance) in the UV and visible domains. Limnol. Oceanogr. 1981, 26, 43–53. [Google Scholar] [CrossRef]
- Nelson, J.R.; Guarda, S. Particulate and dissolved spectral absorption on the continental shelf of the southeastern United States. J. Geophys. Res. 1995, 100, 8715–8732. [Google Scholar] [CrossRef]
- Coble, P. Marine Optical Biogeochemistry: The Chemistry of Ocean Color. Chem. Rev. 2007, 107, 402–418. [Google Scholar] [CrossRef] [PubMed]
- Swan, C.M.; Siegel, D.A.; Nelson, N.B.; Carlson, C.A.; Nasir, E. Biogeochemical and hydrographic controls on chromophoric dissolved organic matter distribution in the Pacific Ocean. Deep-Sea Res. I 2009, 56, 2175–2192. [Google Scholar] [CrossRef]
- Nelson, N.B.; Siegel, D.A.; Carlson, C.A.; Swan, C.M. Tracing global biogeochemical cycles and meridional overturning circulation using chromophoric dissolved organic matter. Geophys. Res Lett. 2010, 37. [Google Scholar] [CrossRef]
- Stedmon, C.A.; Osburn, C.L.; Gragh, T. Tracing water mass mixing in the Baltic–North Sea transition zone using the optical properties of coloured dissolved organic matter. Estuar. Coast. Shelf Sci. 2010, 87, 156–162. [Google Scholar] [CrossRef]
- Del Castillo, C.E.; Coble, P.G.; Morell, J.M.; López, J.M.; Corredor, J.E. Analysis of the optical properties of the Orinoco River plume by absorption and fluorescence spectroscopy. Mar. Chem. 1999, 66, 35–51. [Google Scholar] [CrossRef]
- Del Vecchio, R.; Blough, N.V. Spatial and seasonal distribution of chromophoric dissolved organic matter (CDOM) and dissolved organic carbon (DOC) in the Middle Atlantic Bight. Mar. Chem. 2004, 89, 169–187. [Google Scholar] [CrossRef]
- Rochelle-Newall, E.J.; Fisher, T.R. Chromophoric dissolved organic matter and dissolved organic carbon in Chesapeake Bay. Mar. Chem. 2002, 77, 23–41. [Google Scholar] [CrossRef]
- Steinberg, D.K.; Nelson, N.; Carlson, C.A.; Prusak, A.C. Production of chromophoric dissolved organic matter (CDOM) in the open ocean by zooplankton and the colonial cyanobacterium Trichodesmium spp. Mar. Ecol. Prog. Ser. 2004, 267, 45–56. [Google Scholar] [CrossRef]
- Andrew, A.A.; Del Vecchio, R.; Subramaniam, A.; Blough, N.V. Chromophoric dissolved organic matter (CDOM) in the equatorial Atlantic Ocean: Optical properties and their relation to CDOM structure and source. Mar. Chem. 2013, 148, 33–43. [Google Scholar] [CrossRef]
- Nelson, N.B.; Siegel, D.A. The global distribution and dynamics of chromophoric dissolved organic matter. Annu. Rev. Mar. Sci. 2013, 5, 447–476. [Google Scholar] [CrossRef] [PubMed]
- Mopper, K.; Keiber, D.J. Photochemistry and the cycling of carbon, sulfur, nitrogen and phosphorus. In Biogeochemistry of Marine Dissolved Organic Matter; Hansel, D.A., Carlson, C.A., Eds.; Academic Press: San Diego, CA, USA, 2002; pp. 455–507. [Google Scholar]
- Moran, M.A.; Sheldon, W.M.; Zepp, R.G. Carbon loss and optical property changes during long-term photochemical and biological degradation of estuarine dissolved organic matter. Limnol. Oceangr. 2000, 45, 1254–1264. [Google Scholar] [CrossRef]
- Boyd, T.J.; Osburn, C.L. Changes in CDOM fluorescence from allochthonous and autochthonous sources during tidal mixing and bacterial degradation in two coastal estuaries. Mar. Chem. 2004, 89, 189–210. [Google Scholar] [CrossRef]
- Carder, K.L.; Chen, F.R.; Lee, Z.P.; Hawes, S.K.; Kamykowski, D. Semianalytic moderate-resolution imaging spectrometer algorithms for chlorophyll and absorption with bio-optical domains based on nitrate-depletion temperatures. J. Geophys. Res. 1999, 104, 5403–5421. [Google Scholar] [CrossRef]
- Hoge, F.E.; Wright, C.W.; Lyon, P.E.; Swift, R.N.; Yungel, J.K. Inherent optical properties imagery of the western North Atlantic Ocean: Horizontal spatial variability of the upper mixed layer. J. Geophys. Res. 2001, 106, 31129–31140. [Google Scholar] [CrossRef]
- Lee, Z.P.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705–2714. [Google Scholar] [CrossRef] [PubMed]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Behrenfeld, M.J. Independence and interdependencies among global ocean color properties: Reassessing the bio-optical assumption. J. Geophys. Res. 2005, 110, C07011. [Google Scholar] [CrossRef]
- Siegel, D.A.; Maritorena, S.; Nelson, N.B.; Behrenfeld, M.J.; McClain, C.R. Colored dissolved organic matter and its influence on the satellite-based characterization of the ocean biosphere. Geophys. Res. Lett. 2005, 32, L20605. [Google Scholar] [CrossRef]
- Doerffer, R.; Schiller, H. The MERIS case 2 water algorithm. Int. J. Remote Sens. 2007, 28, 517–535. [Google Scholar] [CrossRef]
- Lee, Z.P.; Arnone, R.A.; Hu, C.; Werdell, P.J.; Lubac, B. Uncertainties of optical parameters and their propagations in an analytical ocean color inversion algorithm. Appl. Opt. 2010, 49, 369–381. [Google Scholar] [CrossRef] [PubMed]
- Bricaud, A.; Ciotti, A.M.; Gentili, B. Spatial-temporal variations in phytoplankton size and colored detrital matter absorption at global and regional scales, as derived from twelve years of SeaWiFS data (1998–2009). Glob. Biogeochem. Cycles 2012, 26, GB1010. [Google Scholar] [CrossRef]
- Tilstone, G.H.; Peters, S.W.M.; Van Der Woerd, H.J.; Eleveld, M.A.; Ruddick, K.; Schönfeld, W.; Krasemann, H.; Martinez-Vicente, V.; Blondeau-Patissier, D.; Röttgers, R.; et al. Variability in specific-absorption properties and their use in a semianalytical ocean colour algorithm for MERIS in north sea and western English channel coastal waters. Remote Sens. Environ. 2012, 118, 320–338. [Google Scholar] [CrossRef]
- Werdell, P.J.; Franz, B.A.; Bailey, S.W.; Feldman, G.C.; Boss, E.; Brando, V.E.; Dowell, M.; Hirata, T.; Lavender, S.J.; Lee, Z.; et al. Generalized ocean color inversion model for retrieving marine inherent optical properties. Appl. Opt. 2013, 52, 2019–2037. [Google Scholar] [CrossRef] [PubMed]
- Aurin, D.A.; Dierssen, H.M. Advantages and limitations of ocean color remote sensing in CDOM-dominated, mineral-rich coastal and estuarine waters. Remote Sens. Environ. 2012, 125, 181–197. [Google Scholar] [CrossRef]
- Dong, Q.; Shang, S.; Lee, Z. An algorithm to retrieve absorption coefficient of chromophoric dissolved organic matter from ocean color. Remote Sens. Environ. 2013, 128, 259–267. [Google Scholar] [CrossRef]
- Matsuoka, A.; Hooker, S.B.; Bricaud, A.; Gentili, B.; Babin, M. Estimating absorption coefficients of colored dissolved organic matter (CDOM) using a semi-analytical algorithm for southern Beaufort Seawaters: Application to deriving concentrations of dissolved organic carbon from space. Biogeosciences 2013, 10, 917–927. [Google Scholar] [CrossRef]
- Mannino, A.; Russ, M.E.; Hooker, S.B. Algorithm development and validation for satellite-derived distributions of DOC and CDOM in the U.S. Middle Atlantic Bight. J. Geophys. Res. 2008, 113, C07051. [Google Scholar] [CrossRef]
- Fichot, C.G.; Kaiser, K.; Hooker, S.B.; Amon, R.M.W.; Babin, M.; Belanger, S.; Walker, S.A.; Benner, R. Pan-Arctic distributions of continental runoff in the Arctic Ocean. Sci. Rep. 2013, 3, 1053. [Google Scholar] [CrossRef] [PubMed]
- Mannino, A.; Novak, M.G.; Hooker, S.B.; Hyde, K.; Aurin, D. Algorithm development and validation of CDOM properties for estuarine and continental shelf waters along the northeastern U.S. coast. Remote Sens. Environ. 2014, 152, 576–602. [Google Scholar] [CrossRef]
- Zhu, W.; Yu, Q.; Tian, Y.Q.; Becker, B.L.; Zheng, T.; Carrick, H. An assessment of remote sensing for colored dissolved organic matter in complex freshwater environments. Remote Sens. Environ. 2014, 140, 766–778. [Google Scholar] [CrossRef]
- Raicich, F. On the fresh water balance of the Adriatic coast. J. Mar. Syst. 1996, 9, 305–319. [Google Scholar] [CrossRef]
- Marini, M.; Fornasiero, P.; Artegiani, A. Variations of Hydrochemical Features in the Coastal Waters of Monte Conero: 1982–1990. Mar. Ecol. 2002, 23, 258–271. [Google Scholar] [CrossRef]
- Campanelli, A.; Fornasiero, P.; Marini, M. Physical and Chemical characterization of water column in the Piceno coastal area (Adriatic Sea). Fresenius Environ. Bull. 2004, 13, 430–435. [Google Scholar]
- Campanelli, A.; Grilli, F.; Paschini, E.; Marini, M. The influence of an exceptional Po River flood on the physical and chemical oceanographic properties of the Adriatic Sea. Dyn. Atmos. Oceans 2011, 52, 284–297. [Google Scholar] [CrossRef]
- Giani, M.; Djakovac, T.; Degobbis, D.; Cozzi, S.; Solidoro, C.; Umani, S.F. Recent changes in the marine ecosystems of the northern Adriatic Sea. Estuar. Coast. Shelf Sci. 2012, 115, 1–13. [Google Scholar] [CrossRef]
- Degobbis, D.; Precali, R.; Ivančić, I.; Smodlaka, N.; Fuks, D.; Kveder, S. Long-term changes in the northern Adriatic ecosystem related to anthropogenic eutrophication. J. Environ. Pollut. 2000, 13, 495–533. [Google Scholar] [CrossRef]
- Marini, M.; Jones, B.H.; Campanelli, A.; Grilli, F.; Lee, C.M. Seasonal variability and Po River plume influence on biochemical properties along western Adriatic coast. J. Geophys. Res. 2008, 113, C05S90. [Google Scholar] [CrossRef]
- Berto, D.; Giani, M.; Savelli, F.; Centanni, E.; Ferrari, C.R.; Pavoni, B. Winter to spring variations of chromophoric dissolved organic matter in a temperate estuary (Po River, northern Adriatic Sea). Mar. Environ. Res. 2010, 70, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Cozzi, S.; Giani, M. River water and nutrient discharges in the Northern Adriatic Sea: Current importance and long term changes. Cont. Shelf Res. 2011, 31, 1881–1893. [Google Scholar] [CrossRef]
- Poulain, P.M.; Raicich, F. Forcings. In Physical Oceanography of the Adriatic Sea; Cushman-Roisin, B., Gacic, M., Poulain, P.M., Artegiani, A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001; pp. 45–65. [Google Scholar]
- Zore-Armanda, M.; Gaćić, M. Effects of Bora on the circulation in the North Adriatic. Ann. Geophys. 1987, 5B, 93–102. [Google Scholar]
- Artegiani, A.; Bregant, D.; Paschini, E.; Pinardi, N.; Raicich, F.; Russo, A. The Adriatic Sea general circulation. Part I. Air-sea interactions and water mass structure. J. Phys. Oceanogr. 1997, 27, 1492–1514. [Google Scholar] [CrossRef]
- Artegiani, A.; Bregant, D.; Paschini, E.; Pinardi, N.; Raicich, F.; Russo, A. The Adriatic Sea general circulation. Part II: Baroclinic Circulation Structure. J. Phys. Oceanogr. 1997, 27, 1515–1532. [Google Scholar]
- Boldrin, A.; Carniel, S.; Giani, M.; Marini, M.; Bernardi Aubry, F.; Campanelli, A.; Grilli, F.; Russo, A. Effects of bora wind on physical and biogeochemical properties of stratified waters in the northern Adriatic. J. Geophys. Res. 2009, 114, C08S92. [Google Scholar] [CrossRef]
- Poulain, P.M.; Cushman-Roisin, B. Circulation. In Physical Oceanography of the Adriatic Sea; Cushman-Roisin, B., Gačič, M., Poulain, P.M., Artegiani, A., Eds.; Kluwier Academic Publisher: Dordrecht, The Netherlands, 2001; pp. 67–109. [Google Scholar]
- Orlić, M.; Gačič, M.; La Violette, P.E. The currents and circulation of the Adriatic Sea. Oceanol. Acta 1992, 15, 109–124. [Google Scholar]
- Kourafalou, V.H. Process studies on the Po River plume, north Adriatic Sea. J. Geophys. Res. 1999, 104, 29963–29985. [Google Scholar] [CrossRef]
- Kourafalou, V.H. River plume development in semi-enclosed Mediterranean regions: North Adriatic Sea and Northwestern Aegean Sea. J. Mar. Syst. 2001, 30, 181–205. [Google Scholar] [CrossRef]
- Jeffries, M.A.; Lee, C.M. A climatology of the northern Adriatic Sea’s response to Bora and river forcing. J. Geophys. Res. 2007, 112, 1–18. [Google Scholar] [CrossRef]
- Sangiorgi, F.; Donders, T.H. Reconstructing 150 years of eutrophication in the north-western Adriatic Sea (Italy) using dinoflagellate cysts, pollen and spores. Estuar. Coast. Shelf Sci. 2004, 60, 69–79. [Google Scholar] [CrossRef]
- Socal, G.; Acri, F.; Bastianini, M.; Bernardi Aubry, F.; Bianchi, F.; Cassin, D.; Coppola, J.; De Lazzari, A.; Bandelj, V.; Cossarini, G.; et al. Hydrological and biogeochemical features of the Northern Adriatic Sea in the period 2003–2006. Mar. Ecol. 2008, 29, 449–468. [Google Scholar] [CrossRef]
- Marini, M.; Campanelli, A.; Sanxhaku, M.; Kljajić, Z.; Betti, M.; Grilli, F. Late spring characterization of different coastal areas of the Adriatic Sea. Acta Adriat. 2015, 56, 27–46. [Google Scholar]
- Specchiulli, A.; Bignami, F.; Marini, M.; Fabbrocini, A.; Scirocco, T.; Campanelli, A.; Penna, P.; Santucci, A.; D’Adamo, R. The role of forcing agents on biogeochemical variability along the southwestern Adriatic coast: The Gulf of Manfredonia case study. Estuar. Coast. Shelf Sci. 2016, 183, 136–149. [Google Scholar] [CrossRef]
- United Nations Educational, Scientific, and Cultural Organization (UNESCO). The Acquisition, Calibration and Analysis of CTD Data; A Report of SCOR WG 51; United Nations Educational, Scientific, and Cultural Organization: Paris, France, 1988; pp. 1–59. [Google Scholar]
- Mitchell, B.G.; Kahru, M.; Wieland, J.; Stramska, M. Determination of spectral absorption coefficient of particles, dissolved material and phytoplankton for discrete water samples. In Ocean Optics Protocols for Satellite Ocean Colour Sensor Validation; NASA/TM-2003-211621/Rev4-Volume IV; Fargion, G.S., Mueller, J.L., McClain, C.R., Eds.; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 39–64. [Google Scholar]
- Vignudelli, S.; Santinelli, C.; Murru, E.; Nainnicini, L.; Seritti, A. Distributions of dissolved organic carbon (DOC) and chromophoric dissolved organic matter (CDOM) in coastal of the northern Tyrrhenian Sea (Italy). Estuar. Coast. Shelf Sci. 2004, 60, 133–149. [Google Scholar] [CrossRef]
- Copernicus Marine Environment Monitoring Service (CMEMS) Online Catalogue. Available online: http://marine.copernicus.eu/services-portfolio/access-to-products/ (accessed on 10 October 2016).
- Volpe, G.; Colella, S.; Forneris, V.; Tronconi, C.; Santoleri, R. The Mediterranean Ocean Colour Observing System—System development and product validation. Ocean Sci. 2012, 8, 869–883. [Google Scholar] [CrossRef]
- Santoleri, R.; Volpe, G.; Marullo, S.; Buongiorno Nardelli, B. Open Waters Optical Remote Sensing of the Mediterranean Sea. In Remote Sensing of the European Seas; Barale, V., Gade, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 103–116. [Google Scholar]
- Mobley, C.D. Estimation of the remote-sensing reflectance from above-surface measurements. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- D’Alimonte, D.; Zibordi, G.; Berthon, J.-B.; Canuti, E.; Kajiyama, T. Performance and applicability of bio-optical algorithms in different European seas. Remote Sens. Environ. 2012, 124, 402–412. [Google Scholar] [CrossRef]
- Braga, F.; Giardino, C.; Bassani, C.; Matta, E.; Candiani, G.; Strombeck, N.; Adamo, M.; Bresciani, M. Assessing water quality in the northern Adriatic Sea from HICO (TM) data. Remote Sens. Lett. 2013, 4, 1028–1037. [Google Scholar] [CrossRef]
- Kajiyama, T.; D’Alimonte, D.; Zibordi, G. Regional algorithms for European Seas: A case study based on MERIS data. IEEE Geosci. Remote Sens. 2013, 10, 283–287. [Google Scholar] [CrossRef]
- Brando, V.E.; Braga, F.; Zaggia, L.; Giardino, C.; Bresciani, M.; Matta, E.; Bellafiore, D.; Ferrarin, C.; Maicu, F.; Benetazzo, A.; et al. High-resolution satellite turbidity and sea surface temperature observations of river plume interactions during a significant flood event. Ocean Sci. 2015, 11, 909–920. [Google Scholar] [CrossRef]
- Sathyendranath, S. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex Waters; Report Number 3; International Ocean-Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2003; pp. 1–140. [Google Scholar]
- D’Sa, E.J.; Miller, R.L. Bio-optical properties in waters influenced by the Mississippi River during low flow conditions. Remote Sens. Environ. 2003, 84, 538–549. [Google Scholar] [CrossRef]
- Belanger, S.; Babin, M.; Larouche, P. An empirical ocean color algorithm for estimating the contribution of chromophoric dissolved organic matter to total light absorption in optically complex waters. J. Geophys. Res. 2008, 113, C04027. [Google Scholar] [CrossRef]
- Del Castillo, C.E.; Miller, R.L. On the use of ocean color remote sensing to measure the transport of dissolved organic carbon by the Mississippi River Plume. Remote Sens. Environ. 2008, 112, 836–844. [Google Scholar] [CrossRef]
- Tiwari, S.P.; Shanmugam, P. An optical model for the remote sensing of coloured dissolved organic matter in coastal/ocean waters. Estuar. Coast. Shelf Sci. 2011, 93, 396–402. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016; Available online: https://www.R-project.org/ (accessed on 22 June 2016).
- Graybill, F.A.; Iyer, H.K. Regression Analysis: Concepts and Applications; Duxbuty Press: Belmont, TN, USA, 1994; p. 3978. [Google Scholar]
- Wooldridge, J.M. Heteroscedasticity. In Introductory Econometrics, 6th ed.; Cengage Learning: Boston, MA, USA, 2016; pp. 240–252. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis, 3rd ed.; John Wiley and Sons: New York, NY, USA, 1998; pp. 280–282. [Google Scholar]
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Mixed Effects Models and Extensions in Ecology with R; Springer: New York, NY, USA, 2009; pp. 74–75. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; p. 171. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. NLME: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-128. 2016. Available online: http://CRAN.R-project.org/package=nlme (accessed on 18 October 2016).
- Christensen, R. Plane Answers to Complex Questions: The Theory of Linear Models, 4th ed.; Springer: New York, NY, USA, 2011; pp. 368–370. [Google Scholar]
- Crawley, M.J. Statistics: An Introduction Using R, 2nd ed.; John Wiley and Sons: Chichester, UK, 2015; pp. 193–202. [Google Scholar]
- Arpa Emilia Romagna-Idro-Meteo-Clima. Available online: https://www.arpae.it/sim/ (accessed on 16 January 2016).
- Harris, C.K.; Sherwood, C.R.; Signell, R.P.; Bever, A.J.; Warner, J.C. Sediment dispersal in the northwestern Adriatic Sea. J. Geophys. Res. 2008, 113, C11S03. [Google Scholar] [CrossRef]
- D’Sa, E.J.; Miller, R.L.; Del Castillo, C. Bio-optical properties and ocean color algorithms for coastal waters influenced by the Mississippi River during a cold front. Appl. Opt. 2006, 45, 7410–7428. [Google Scholar] [CrossRef] [PubMed]
- Komick, N.M.; Costa, M.P.F.; Gower, J. Bio-optical algorithm evaluation for MODIS for western Canada coastal waters: An exploratory approach using in situ reflectance. Remote Sens. Environ. 2009, 113, 794–804. [Google Scholar] [CrossRef]
- Kutsera, T.; Piersona, D.C.; Kalliob, K.Y.; Reinarta, A.; Sobek, S. Mapping lake CDOM by satellite remote sensing. Remote Sens. Environ. 2005, 94, 535–540. [Google Scholar] [CrossRef]
- Mobley, C.D.; Sundman, L.K. HydroLight 5.2-EcoLight 5.2 Technical Documentation (2013); Sequoia Scientific, Inc.: Bellevue, WA, USA, 2013; Available online: http://www.oceanopticsbook.info/view/references/publications (accessed on 15 October 2016).











| Region | Cruise | Dates | No. of Measurements |
|---|---|---|---|
| aCDOM, S | |||
| Zone A | Ritmare A | 29 November 2013 | 6 |
| Zone B | ANOC14_1 | 13 February 2014 | 4 |
| Zone B | ANOC14_2 | 21 Marh 2014 | 5 |
| Zone A | Balmas 1 | 25 March 2014 | 3 |
| Zone B | Balmas 2 | 24 May 2014 | 4 |
| Zone B | Balmas 3 | 21–22 August 2014 | 3 |
| Zone C | Ecosee/a 1 | 26 August 2014 | 15 |
| Zone A | ANOC_4 | 22 September 2014 | 7 |
| Zone C | Ecosee/a 2 | 7 October 2014 | 6 |
| Zone B | Ecosee/a 3 | 17 October 2014 | 4 |
| Zone B | Balmas 4 | 29 October 2014 | 3 |
| Zone A | Ritmare B | 11–12 December 2014 | 18 |
| Zone B | ANOC15_1 | 11 February 2015 | 6 |
| Zone B | ANOC15_2 | 14 March 2015 | 4 |
| Zone B | ANOC15_2 | 6 May 2015 | 5 |
| Zone B | Ecosee/a 4 | 22 July 2015 | 11 |
| Zone B | ANOC15_4 | 18 September 2015 | 7 |
| Zone B | Escavo AN | 10 November 2015 | 10 |
| Zone A | Solemon2015 | 29 November 2015 | 2 |
| Zone B | ANOC16_1 | 11 February 2016 | 7 |
| Zone B | ANOC16_2 | 18–19 March 2016 | 15 |
| Zone A | Ritmare C | 28–29 April 2016 | 7 |
| Zone B | ANOC16_4 | 18 June 2016 | 6 |
| Zone A | Medias2016 | 23 June 2016 | 6 |
| Zone C | Post-Ecosee/a | 15 July 2016 | 8 |
| Region | aCDOM355 (m−1) | S | n | ||
|---|---|---|---|---|---|
| Mean | s.d. | Mean | s.d. | ||
| Zone A | 0.81 | 0.49 | 31.75 | 5.25 | 42 |
| Zone B | 0.38 | 0.30 | 36.27 | 2.26 | 99 |
| Zone C | 0.38 | 0.16 | 35.16 | 0.52 | 29 |
| Parameter | Parameter Estimate | Standard Error | t-Value | p |
|---|---|---|---|---|
| b1 | 0.22966 | 0.08290 | 2.770 | 0.006831 * |
| b2 | 0.01374 | 0.03707 | 0.371 | 0.711856 |
| b3 | 0.26675 | 0.24283 | 1.098 | 0.274996 |
| b4 | 1.63251 | 0.47735 | 3.420 | 0.000951 * |
| b5 | −0.18052 | 0.15756 | −1.146 | 0.255012 |
| Parameter (Model 1) | Parameter Estimate | Standard Error | t-Value | p |
|---|---|---|---|---|
| b1 | 0.1165 | 0.0226 | 5.157 | 1.46 × 10−6 * |
| b2 | 1.9089 | 0.0857 | 22.273 | <2 × 10−16 * |
| Parameter (Model 2) | Parameter Estimate | Standard Error | t-Value | p |
|---|---|---|---|---|
| b1 | 0.42387 | 0.01403 | 30.21 | <2 × 10−16 * |
| b2 | 1.15761 | 0.05321 | 21.75 | <2 × 10−16 * |
| Parameter (Model 3) | Parameter Estimate | Standard Error | t-Value | p |
|---|---|---|---|---|
| b1 | 0.18325 | 0.01552 | 11.81 | <2 × 10−16 * |
| b2 | 1.48088 | 0.11732 | 12.62 | <2 × 10−16 * |
| Parameter (Model 4) | Parameter Estimate | Standard Error | t-Value | p |
|---|---|---|---|---|
| b1 | −0.39669 | 0.07517 | −5.277 | 1.05 × 10−6 * |
| b2 | 2.18707 | 0.74484 | 2.936 | 0.004309 * |
| b3 | −5.50891 | 1.12927 | −4.878 | 5.18 × 10−6 * |
| b4 | 1.70642 | 0.12586 | 13.55 | <2 × 10−16 * |
| b5 | 0.06978 | 0.01424 | 4.901 | 4.74 × 10−6 * |
| b6 | 3.18145 | 1.13802 | 2.796 | 0.006450 * |
| b7 | 13.1729 | 3.34276 | 3.941 | 0.000170 * |
| b8 | −0.74416 | 0.10134 | −7.343 | 1.37 × 10−10 * |
| b9 | −1.15771 | 0.27683 | −4.182 | 7.20 × 10−5 * |
| b10 | 3.41274 | 0.61429 | 5.556 | 3.34 × 10−7 * |
| b11 | −13.29309 | 3.88291 | −3.423 | 0.000967 * |
| Algorithm | Adjusted R2 | APD | RMSE (m−1) |
|---|---|---|---|
| Model 1 | 0.8426 | 33 (28) * | 0.1421 |
| Model 2 | 0.8322 | 31 (24) | 0.1482 |
| Model 3 | 0.8426 | 35 (31) | 0.1496 |
| Model 4 | 0.5528 | 72 (65) | 0.3344 |
| Mannino et al. [37] | 0.5594 | 28 (23) | 0.2580 |
| Del Castillo and Miller [78] | 0.0098 | 74 (71) | 0.3541 |
| D’Sa and Miller [76] | 0.4122 | 39 (30) | 0.2922 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campanelli, A.; Pascucci, S.; Betti, M.; Grilli, F.; Marini, M.; Pignatti, S.; Guicciardi, S. An Empirical Ocean Colour Algorithm for Estimating the Contribution of Coloured Dissolved Organic Matter in North-Central Western Adriatic Sea. Remote Sens. 2017, 9, 180. https://doi.org/10.3390/rs9020180
Campanelli A, Pascucci S, Betti M, Grilli F, Marini M, Pignatti S, Guicciardi S. An Empirical Ocean Colour Algorithm for Estimating the Contribution of Coloured Dissolved Organic Matter in North-Central Western Adriatic Sea. Remote Sensing. 2017; 9(2):180. https://doi.org/10.3390/rs9020180
Chicago/Turabian StyleCampanelli, Alessandra, Simone Pascucci, Mattia Betti, Federica Grilli, Mauro Marini, Stefano Pignatti, and Stefano Guicciardi. 2017. "An Empirical Ocean Colour Algorithm for Estimating the Contribution of Coloured Dissolved Organic Matter in North-Central Western Adriatic Sea" Remote Sensing 9, no. 2: 180. https://doi.org/10.3390/rs9020180
APA StyleCampanelli, A., Pascucci, S., Betti, M., Grilli, F., Marini, M., Pignatti, S., & Guicciardi, S. (2017). An Empirical Ocean Colour Algorithm for Estimating the Contribution of Coloured Dissolved Organic Matter in North-Central Western Adriatic Sea. Remote Sensing, 9(2), 180. https://doi.org/10.3390/rs9020180