SAR-PC: Edge Detection in SAR Images via an Advanced Phase Congruency Model
Abstract
:1. Introduction
2. Review of the Phase Congruency
3. Methodology
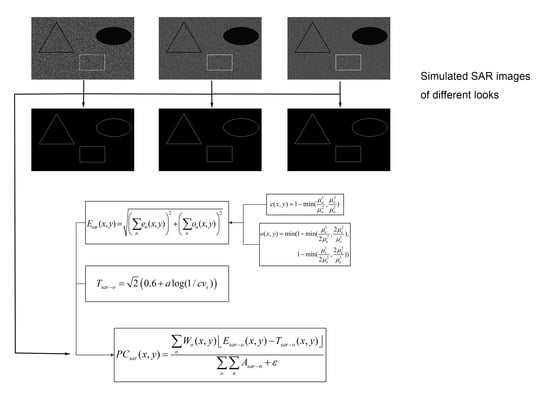
3.1. SAR Local Energy Model
3.2. Noise Estimation
4. Experimental Results
4.1. Parameter Settings
4.2. Comparison on Simulated SAR Images
4.3. Comparison on Satellite SAR Images
5. Discussion
5.1. Discussion On Simulated SAR Images
5.2. Discussion On Satellite SAR Images
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SAR | Synthetic Aperture Radar |
| PC | Phase Congruency |
| SAR-PC | SAR Phase Congruency |
| ROC | Receiver Operating Characteristic |
| CFAR | Constant False Alarm Rate |
| ROA | Ratio Of Averages |
| MSP-ROA | Maximum Strength edge Pruned Ratio Of Averages |
| ROEWA | Ratio Of Exponentially Weighted Averages |
| GSS | Gaussian-Gamma-Shaped |
| RBED | Ratio-Based Edge Detector |
| RL | Ratio Line |
| probability density function | |
| Probability of detection | |
| coefficient of variation | |
| PFA | Probability of False Alarm |
| GT | Ground Truth |
| True Positive | |
| False Positive | |
| True Negative | |
| False Negative | |
| True Positive Rate | |
| False Positive Rate |
Appendix A. The Derivation Process of the Relationship Between cv and Cr
References
- Touzi, R.; Lopes, A.; Bousquet, P. A statistical and geometrical edge detector for SAR images. IEEE Trans. Geosci. Remote Sens. 1988, 26, 764–773. [Google Scholar] [CrossRef]
- Amirmazlaghani, M.; Amindavar, H.; Moghaddamjoo, A. Speckle suppression in SAR images using the 2-D GARCH model. IEEE Trans. Image Process. 2009, 18, 250–259. [Google Scholar] [CrossRef] [PubMed]
- Bovik, A.C. On detecting edges in speckle imagery. IEEE Trans. Acoust. Speech Signal Process. 1988, 36, 1618–1627. [Google Scholar] [CrossRef]
- Ganugapati, S.; Moloney, C. A ratio edge detector for speckled images based on maximum strength edge pruning. In Proceedings of the 1995 International Conference on Image Processing, Washington, DC, USA, 23–26 October 1995; Volume 2, pp. 165–168.
- Fjortoft, R.; Lopes, A.; Marthon, P.; Cubero-Castan, E. An optimal multiedge detector for SAR image segmentation. IEEE Trans. Geosci. Remote Sens. 1998, 36, 793–802. [Google Scholar] [CrossRef]
- Shui, P.L.; Cheng, D. Edge detector of SAR images using Gaussian-Gamma-shaped bi-windows. IEEE Geosci. Remote Sens. Lett. 2012, 9, 846–850. [Google Scholar] [CrossRef]
- Wei, Q.R.; Feng, D.Z. An efficient SAR edge detector with a lower false positive rate. Int. J. Remote Sens. 2015, 36, 3773–3797. [Google Scholar] [CrossRef]
- Tupin, F.; Maitre, H.; Mangin, J.F.; Nicolas, J.M.; Pechersky, E. Detection of linear features in SAR images: Application to road network extraction. IEEE Trans. Geosci. Remote Sens. 1998, 36, 434–453. [Google Scholar] [CrossRef]
- Wei, Q.R.; Feng, D.Z. Extracting line features in SAR images through image edge fields. IEEE Geosci. Remote Sens. Lett. 2016, 13, 540–544. [Google Scholar] [CrossRef]
- Sun, J.; Mao, S. River detection algorithm in SAR images based on edge extraction and ridge tracing techniques. Int. J. Remote Sens. 2011, 32, 3485–3494. [Google Scholar] [CrossRef]
- Fu, X.; You, H.; Fu, K. A statistical approach to detect edges in SAR images based on square successive difference of averages. IEEE Geosci. Remote Sens. Lett. 2012, 9, 1094–1098. [Google Scholar] [CrossRef]
- Wei, Q.R.; Feng, D.Z.; Xie, H. Edge detector of SAR images using crater-shaped window with edge compensation strategy. IEEE Geosci. Remote Sens. Lett. 2016, 13, 38–42. [Google Scholar] [CrossRef]
- Ma, X.; Liu, S.; Hu, S.; Geng, P.; Liu, M.; Zhao, J. SAR image edge detection via sparse representation. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Tison, C.; Tupin, F.; Maitre, H. Retrieval of building shapes from shadows in high resolution SAR interferometric images. In Proceedings of the 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 3, pp. 1788–1791.
- Thiele, A.; Cadario, E.; Schulz, K.; Thonnessen, U.; Soergel, U. Building recognition from multi-aspect high-resolution InSAR data in urban areas. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3583–3593. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G.; Reale, D. Edge detection using real and imaginary decomposition of SAR data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3833–3842. [Google Scholar] [CrossRef]
- Ferraioli, G. Multichannel InSAR building edge detection. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1224–1231. [Google Scholar] [CrossRef]
- Baselice, F.; Ferraioli, G. Statistical edge detection in urban areas exploiting SAR complex data. IEEE Geosci. Remote Sens. Lett. 2012, 9, 185–189. [Google Scholar] [CrossRef]
- Morrone, M.C.; Owens, R.A. Feature detection from local energy. Pattern Recognit. Lett. 1987, 6, 303–313. [Google Scholar] [CrossRef]
- Kovesi, P. Invariant Measures of Image Features from Phase Information; University of Western Australia: Crawley, Australia, 1996. [Google Scholar]
- Kovesi, P. Phase congruency detects corners and edges. In Proceedings of the Digital Image Computing: Techniques and Applications 2003, Sydney, Australia, 10–12 December 2003.
- Mulet-Parada, M.; Noble, J.A. 2D+ T acoustic boundary detection in echocardiography. Med. Image Anal. 2000, 4, 21–30. [Google Scholar] [CrossRef]
- Venkatesh, S.; Owens, R. An energy feature detection scheme. In Proceedings of the ICIP’89: IEEE International Conference on Image Processing, Singapore, 5–8 September 1989.
- Kovesi, P. Image features from phase congruency. Videre J. Comput. Vis. Res. 1999, 1, 1–26. [Google Scholar]
- Weisstein, E.W. CRC Concise Encyclopedia of Mathematics; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Wong, A.; Clausi, D.A. ARRSI: Automatic registration of remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1483–1493. [Google Scholar] [CrossRef]
- Fan, J.; Wu, Y.; Wang, F.; Zhang, Q.; Liao, G.; Li, M. SAR image registration using phase congruency and nonlinear diffusion-based SIFT. IEEE Geosci. Remote Sens. Lett. 2015, 12, 562–566. [Google Scholar]
- Zhang, Z.; Wang, X.; Xu, L. Target detection in SAR images based on sub-aperture coherence and phase congruency. Intell. Autom. Soft Comput. 2012, 18, 831–843. [Google Scholar] [CrossRef]
- Făgădar-Cosma, M.; Micea, M.V.; Creţu, V. Obtaining highly localized edges using phase congruency and ridge detection. In Proceedings of the 2010 International Joint Conference on Computational Cybernetics and Technical Informatics (ICCC-CONTI), Timisoara, Romania, 27–29 May 2010; pp. 339–342.
- Xiao, P.F.; Feng, X.Z.; Zhao, S.H.; She, J.F. Segmentation of high-resolution remotely sensed imagery based on phase congruency. Acta Geod. Cartogr. Sin. 2007, 2, 146–151. [Google Scholar]
- Mehrotra, R.; Namuduri, K.R.; Ranganathan, N. Gabor filter-based edge detection. Pattern Recognit. 1992, 25, 1479–1494. [Google Scholar] [CrossRef]
- Jiang, W.; Lam, K.M.; Shen, T.Z. Efficient edge detection using simplified Gabor wavelets. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2009, 39, 1036–1047. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.R.; Feng, D.Z.; Yuan, M.D. Automatic local thresholding algorithm for SAR image edge detection. In Proceedings of the 2013 IET International Radar Conference, Xi’an, China, 14–16 April 2013; pp. 1–5.
- Bowyer, K.; Kranenburg, C.; Dougherty, S. Edge detector evaluation using empirical ROC curves. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; Volume 1, pp. 354–359.
- Heath, M.; Sarkar, S.; Sanocki, T.; Bowyer, K. Comparison of edge detectors: A methodology and initial study. In Proceedings of the CVPR IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 18–20 June 1996; pp. 143–148.


















| Detectors: | RBED | GSS | RL | PC | Log-PC | SAR-PC |
|---|---|---|---|---|---|---|
| Time (s) | 0.22 | 0.25 | 0.15 | 0.85 | 0.85 | 0.92 |
| Detectors: | RBED | GSS | PC | Log-PC | SAR-PC |
|---|---|---|---|---|---|
| Time (s) | 0.30 | 0.23 | 1.29 | 1.29 | 1.34 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiang, Y.; Wang, F.; Wan, L.; You, H. SAR-PC: Edge Detection in SAR Images via an Advanced Phase Congruency Model. Remote Sens. 2017, 9, 209. https://doi.org/10.3390/rs9030209
Xiang Y, Wang F, Wan L, You H. SAR-PC: Edge Detection in SAR Images via an Advanced Phase Congruency Model. Remote Sensing. 2017; 9(3):209. https://doi.org/10.3390/rs9030209
Chicago/Turabian StyleXiang, Yuming, Feng Wang, Ling Wan, and Hongjian You. 2017. "SAR-PC: Edge Detection in SAR Images via an Advanced Phase Congruency Model" Remote Sensing 9, no. 3: 209. https://doi.org/10.3390/rs9030209
APA StyleXiang, Y., Wang, F., Wan, L., & You, H. (2017). SAR-PC: Edge Detection in SAR Images via an Advanced Phase Congruency Model. Remote Sensing, 9(3), 209. https://doi.org/10.3390/rs9030209