Mapping Forest Ecosystem Biomass Density for Xiangjiang River Basin by Combining Plot and Remote Sensing Data and Comparing Spatial Extrapolation Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sets
2.2.1. Forest Inventory Data
2.2.2. Remote Sensing Data
2.3. Methods
2.3.1. Extraction and Selection of Spectral Variables
2.3.2. Multivariate Linear Regression (MLR) and Logistic Regression (LR) Model
2.3.3. kNN Algorithms
2.3.4. Leave-One-Out Cross-Validation (LOOCV) and Model Evaluation
3. Results
3.1. Independent Variables of Models
3.2. Multivariate Linear Regression (MLR) Modeling
3.3. Logistic Regression (LR) Modeling
3.4. kNN Modeling
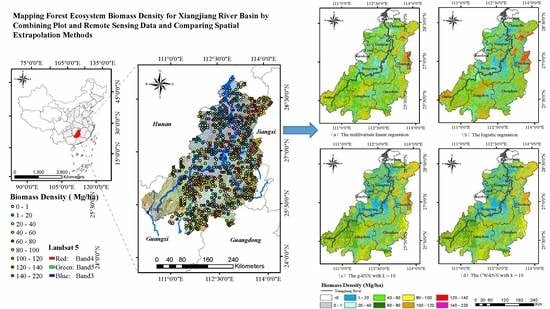
3.5. Spatial Distribution of AGB
4. Discussion
4.1. Rationality of Spectral Variable Selection
4.2. Comparison of Different Methods for Biomass Estimation
4.3. Spatial Distribution of AGB in the Xiangjiang River Basin
4.4. Comparison with Previous Biomass Estimations
4.5. Uncertainty Analysis of Forest Biomass
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AGB | aboveground biomass density |
| kNN | the k-nearest neighbors algorithm |
| LOOCV | Leave-one-out cross-validation |
| LR | Logistic regression model |
| MLR | Multivariate linear regression model |
| NDVI | normalized difference vegetation index |
| SVI | spectral vegetation index |
| MSAVI | modified soil-adjusted vegetation index |
| MNDVI | modified normalized difference vegetation index |
| DVI | difference vegetation index |
| TVI | transformed vegetation index |
| RSR | reduced simple ratio |
| ARVI | atmospherically resistant vegetation index |
| VARI | visible atmospherically resistant index |
| EVI | enhanced vegetation index |
Appendix



References
- Xiang, W.H.; Tian, D.L.; Yan, W.D. Review of researches on forest biomass and productivity. J. Cent. South For. Invent. Plan. 2003, 22, 57–60. (In Chinese) [Google Scholar]
- Hu, Y.; Su, Z.; Li, W.; Li, J.; Ke, X. Influence of tree species composition and community structure on carbon density in a subtropical forest. PLoS ONE 2015, 10, e0136984. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, S.; Hogg, E.H.; Lieffers, V.; Qin, Y.; He, F. Estimating spatial variation in Alberta forest biomass from a combination of forest inventory and remote sensing data. Biogeosciences 2014, 11, 2793–2808. [Google Scholar] [CrossRef] [Green Version]
- Lu, D. The potential and challenge of remote sensing-based biomass estimation. Int. J. Remote Sens. 2006, 27, 1297–1328. [Google Scholar] [CrossRef]
- Klinge, H.; Rodrigues, W.A.; Brunig, E.; Fittkau, E.J. Biomass and structure in a Central Amazonian rain forest. In Ecological Studies: Tropical Ecological Systems; Golley, F.B., Medina, E., Eds.; Springer: Berlin, Germany, 1975; pp. 115–122. [Google Scholar]
- Huxley, J.S. The variation in the width of the abdomen in immature fiddler crabs considered in relation to its relative growth–rate. Am. Nat. 1924, 58, 468–475. [Google Scholar] [CrossRef]
- Brown, S.; Gillespie, A.; Lugo, A. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar]
- Ketterings, Q.M.; Coe, R.; van Noordwijk, M.; Palm, C.A. Reducing uncertainty in the use of allometric biomass equations for predicting above-ground tree biomass in mixed secondary forests. For. Ecol. Manag. 2001, 146, 199–209. [Google Scholar] [CrossRef]
- Geudens, G.; Staelens, J.; Kint, V.; Goris, R.; Lust, N. Allometric biomass equations for Scots pine (Pinus sylvestris L.) seedlings during the first years of establishment in dense natural regeneration. Ann. For. Sci. 2004, 61, 653–659. [Google Scholar] [CrossRef]
- Bi, H.; Turner, J.; Lambert, M.J. Additive biomass equations for native eucalypt forest trees of temperate Australia. Trees 2004, 18, 467–479. [Google Scholar] [CrossRef]
- Kenzo, T.; Furutani, R.; Hattori, D.; Kendawang, J.J.; Tanaka, S.; Sakurai, K.; Ninomiya, I. Allometric equations for accurate estimation of above-ground biomass in logged-over tropical rainforests in Sarawak, Malaysia. J. For. Res. 2009, 14, 365–372. [Google Scholar] [CrossRef]
- Tinker, D.; Stakes, G.K.; Arcano, R.M. Allometric equation development, biomass, and aboveground productivity in ponderosa pine forests, Black Hills, Wyoming. West. J. Appl. For. 2010, 25, 112–119. [Google Scholar]
- Blujdea, V.N.B.; Pilli, R.; Dutca, I.; Ciuvat, L.; Abrudan, I.V. Allometric biomass equations for young broadleaved trees in plantations in Romania. For. Ecol. Manag. 2012, 264, 172–184. [Google Scholar] [CrossRef]
- Penman, J.; Gytarsky, M.; Hiraishi, T.; Krug, T.; Kruger, D.; Pipatti, R.; Buendia, L.; Miwa, K.; Ngara, T.; Tanabe, K.; et al. Definitions and methodological options to inventory emissions from direct human-induced degradation of forests and devegetation of other vegetation types. In Good Practice Guidance for Land Use, Land-Use Change and Forestry; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland; Institute for Global Environmental Strategies (IGES): Hayama, Japan, 2003. [Google Scholar]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef] [PubMed]
- Fang, J.Y.; Wang, Z.M. Forest biomass estimation at regional and global levels, with special reference to China’s forest biomass. Ecol. Res. 2001, 16, 587–592. [Google Scholar] [CrossRef]
- Paustian, K.; Ravindranath, N.H.; Amstel, A.R.V. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2006. [Google Scholar]
- Cohen, W.B.; Goward, S.N. Landsat’s role in ecological applications of remote sensing. BioScience 2004, 54, 535–545. [Google Scholar] [CrossRef]
- Boudreau, J.; Nelson, R.F.; Margolis, H.A.; Beaudoin, A.; Guindon, L.; Kimes, D.S. Regional aboveground forest biomass using airborne and spaceborne LiDAR in Quebec. Remote Sens. Environ. 2008, 112, 3876–3890. [Google Scholar] [CrossRef]
- Lucas, R.M.; Mitchell, A.L.; Armston, J. Measurement of forest above-ground biomass using active and passive remote sensing at large (subnational to global) scales. Curr. For. Rep. 2015, 1, 162–177. [Google Scholar] [CrossRef]
- Kobayashi, S.; Sanga-Ngoie, K. The integrated radiometric correction of optical remote sensing imageries. Int. J. Remote Sens. 2008, 29, 5957–5985. [Google Scholar] [CrossRef]
- Liu, J.K.; Shih, P.T. Topographic correction of wind-driven rainfall for landslide analysis in Central Taiwan with validation from aerial and satellite optical images. Remote Sens. 2013, 5, 2571–2589. [Google Scholar] [CrossRef]
- Harrell, P.; Bourgeau-Chavez, L.L.; Kasischke, E.S.; French, N.H.F.; Christensen, N.L. Sensitivity of ERS-1 and JERS-1 radar data to biomass and stand structure in Alaskan boreal forest. Remote Sens. Environ. 1995, 54, 247–260. [Google Scholar] [CrossRef]
- Konovalyuk, M.; Gorbunova, A.; Baev, A.; Kuznetsov, Y. Parametric reconstruction of radar image based on Multi-point Scattering Model. Int. J. Microw. Wirel. Trans. 2014, 6, 543–548. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S. Lidar-based mapping of leaf area index and its comparison with satellite GLOBCARBON LAI Products. Remote Sens. Environ. 2009, 113, 1628–1645. [Google Scholar] [CrossRef]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm. 2010, 65, 581–590. [Google Scholar] [CrossRef]
- Olsoy, P.J.; Glenn, N.F.; Clark, P.E.; Derryberry, D.R. Aboveground total and green biomass of dryland shrub derived from terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2014, 88, 166–173. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.W. Multi-temporal terrestrial laser scanning for modeling tree biomass change. For. Ecol. Manag. 2014, 318, 304–317. [Google Scholar] [CrossRef]
- Sun, G.; Ranson, K.J.; Kharuk, V.I. Radiometric slope correction for forest biomass estimation from SAR data in the western Sayani Mountains, Siberia. Remote Sens. Environ. 2002, 79, 279–287. [Google Scholar] [CrossRef]
- Neilson, E.T.; MacLean, D.A.; Meng, F.R.; Arp, P.A. Spatial distribution of carbon in natural and management stands in an industrial forest in New Brunswick, Canada. For. Ecol. Manag. 2007, 253, 148–160. [Google Scholar] [CrossRef]
- Nafiseh, G.; Mahmod, R.S.; Mohammadzadeh, A. A review on biomass estimation methods using synthetic aperture radar data. Int. J. Geomat. Geosci. 2011, 1, 776–788. [Google Scholar]
- Sinha, S.; Jeganathan, C.; Sharma, L.K.; Nathawat, M.S. A review of radar remote sensing for biomass estimation. Int. J. Environ. Sci. Technol. 2015, 12, 1779–1792. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2014, 9, 1–43. [Google Scholar] [CrossRef]
- Wang, G.; Oyana, T.; Zhang, M.; Adu-Prah, S.; Zeng, S.; Lin, H.; Se, J. Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images. For. Ecol. Manag. 2009, 258, 1275–1283. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, M.; Gertner, G.Z.; Oyana, T.; McRoberts, R.E.; Ge, H. Uncertainties of mapping forest carbon due to plot locations using national forest inventory plot and remotely sensed data. Scand. J. For. Res. 2011, 26, 360–373. [Google Scholar] [CrossRef]
- Wang, C.; Wang, S.; Guo, Z.; Wang, L.; Ma, C. Study on classification method of hyperspectral remote sensing image based on hierarchical multinomial logistic regression algorithm. Int. J. Earth Sci. Eng. 2014, 7, 415–420. [Google Scholar]
- Tomppo, E.; Halme, M. Using coarse scale forest variables as ancillary information and weighting of variables in k-NN estimation: A genetic algorithm approach. Remote Sens. Environ. 2004, 92, 1–20. [Google Scholar] [CrossRef]
- Tomppo, E.O.; Gagliano, C.; de Natale, F.; Katila, M.; McRoberts, R. Predicting categorical forest variables using an improved k-Nearest Neighbour estimator and Landsat imagery. Remote Sens. Environ. 2009, 113, 500–517. [Google Scholar] [CrossRef]
- Foody, G.M.; Cutler, M.E.; Mcmorrow, J.; Pelz, D.; Tangki, H.; Boyd, D.S.; Douglas, I. Mapping the biomass of Bornean tropical rain forest from remotely sensed data. Glob. Ecol. Biogeogr. 2001, 10, 379–387. [Google Scholar] [CrossRef]
- Almeida, A.C.; Barros, P.L.C.; Monteiro, J.H.A.; Rocha, B.R.P. Estimation of above-ground forest biomass in Amazonia with neural networks and remote sensing. IEEE Lat. Am. Trans. 2009, 7, 27–32. [Google Scholar] [CrossRef]
- Feng, Y.M.; Lei, X.D.; Lu, Y.C. Interpretation of pixel-missing patch of remote sensing image with Kriging interpolation of spatial statistics. J. Remote Sens. 2004, 8, 317–322. [Google Scholar]
- Saatchi, S.; Halligan, K.; Despain, D.; Crabtree, R. Estimation of forest fuel load from radar remote sensing. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1726–1740. [Google Scholar] [CrossRef]
- Saatchi, S.; Marlier, M.; Chazdon, R.L.; Clark, D.B.; Russell, A.E. Impact of spatial variability of tropical forest structure on radar estimation of aboveground biomass. Remote Sens. Environ. 2011, 115, 2836–2849. [Google Scholar] [CrossRef]
- Meng, Q.; Borders, B.; Madden, M. High-resolution satellite image fusion using regression Kriging. Int. J. Remote Sens. 2010, 31, 1857–1876. [Google Scholar] [CrossRef]
- Diao, Y.; Zhang, C.; Liu, J.; Liang, Y.; Hou, X.; Gong, X. Optimization model to estimate Mount Tai forest biomass based on remote sensing. IFIP Adv. Inf. Commun. Technol. 2011, 370, 453–459. [Google Scholar]
- Lee, J.H.; Im, J.H.; Kim, K.M.; Heo, J. Change Analysis of aboveground forest carbon stocks according to the land cover change using multi-temporal Landsat TM images and machine learning algorithms. J. Korean Assoc. Geogr. Inf. Stud. 2015, 18, 81–99. [Google Scholar] [CrossRef]
- Jackett, C.J.; Turner, P.J.; Lovell, J.L.; Williams, R.N. Deconvolution of MODIS imagery using multiscale maximum entropy. Remote Sens. Lett. 2011, 2, 179–187. [Google Scholar] [CrossRef]
- Li, W.K.; Guo, Q.H. A maximum entropy approach to one-class classification of remote sensing imagery. Int. J. Remote Sens. 2010, 31, 2227–2235. [Google Scholar] [CrossRef]
- Rodríguez-Veiga, P.; Saatchi, S.; Tansey, K.; Balzter, H. Magnitude, spatial distribution and uncertainty of forest biomass stocks in Mexico. Remote Sens. Environ. 2016, 183, 265–281. [Google Scholar] [CrossRef]
- Mcroberts, R.E.; Tomppo, E.O. Remote sensing support for national forest inventories. Remote Sens. Environ. 2007, 110, 412–419. [Google Scholar] [CrossRef]
- Mcroberts, R.E.; Næsset, E.; Gobakken, T. Optimizing the k-nearest neighbors technique for estimating forest aboveground biomass using airborne laser scanning data. Remote Sens. Environ. 2015, 163, 13–22. [Google Scholar] [CrossRef]
- Buma, B.; Krapek, J.; Edwards, R.T. Watershed-scale forest biomass distribution in a perhumid temperate rainforest as driven by topographic, soil, and disturbance variables. Can. J. For. Res. 2016, 46, 844–854. [Google Scholar] [CrossRef]
- Zhao, L.; Xiang, W.; Li, J.; Lei, P.; Deng, X.; Fang, X.; Peng, C. Effects of topographic and soil factors on woody species assembly in a Chinese subtropical evergreen broadleaved forest. Forests 2015, 6, 650–669. [Google Scholar] [CrossRef]
- Tang, X.; Fehrmann, L.; Guan, F.; Forrester, D.I.; Guisasola, R.; Kleinn, C. Inventory-based estimation of forest biomass in Shitai County, China: A comparison of five methods. Ann. For. Res. 2016, 59, 269–280. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, K.L.; Wang, Q.X. Using SWAT to simulate runoff under different land use scenarios in Xiangjiang River Basin. Chin. J. Eco-Agric. 2011, 19, 1431–1436. [Google Scholar] [CrossRef]
- Li, H.K.; Lei, Y.C. Estimation and Evaluation of Forest Biomass Carbon Storage in China; China Forestry Press: Beijing, China, 2010. (In Chinese) [Google Scholar]
- Fan, W.Y.; Zhang, H.Y.; Yu, Y.; Mao, X.G.; Yang, J.M. Comparison of three models of forest biomass estimation. Chin. J. Plant Ecol. 2011, 35, 402–410. (In Chinese) [Google Scholar] [CrossRef]
- Sun, H.; Qie, G.P.; Wang, G.X.; Tan, Y.F.; Li, J.P.; Peng, Y.G.; Ma, Z.G.; Luo, C.Q. Increasing the accuracy of mapping urban forest carbon density by combining spatial modeling and spectral unmixing analysis. Remote Sens. 2015, 7, 15114–15139. [Google Scholar] [CrossRef]
- Gao, H.X. Applied Multivariate Statistical Analysis, 1st ed.; Peking University Press: Beijing, China, 2005; pp. 125–220. (In Chinese) [Google Scholar]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013; Available online: http://www.R-project.org/ (accessed on 18 October 2016).
- Vincent, G.; Sabatier, D.; Blanc, L.; Chave, J.; Weissenbacher, E.; Pélissier, R.; Fonty, E.; Molino, J.F.; Couteron, P. Accuracy of small footprint airborne LiDAR in its predictions of tropical moist forest stand structure. Remote Sens. Environ. 2012, 125, 23–33. [Google Scholar] [CrossRef]
- He, Q.; Chen, E.; An, R.; Li, Y. Above-ground biomass and biomass components estimation using LiDAR data in a coniferous forest. Forests 2013, 4, 984–1002. [Google Scholar] [CrossRef]
- Atkinson, P.M.; Massari, R. Generalised linear modelling of susceptibility to landsliding in the central Apennines, Italy. Comput. Geosci. 1998, 24, 373–385. [Google Scholar] [CrossRef]
- Wang, J.C.; Guo, Z.G. Logistic Regression Models: Methods and Application; Higher Education Press: Beijing, China, 2001; pp. 1–17. (In Chinese) [Google Scholar]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef] [Green Version]
- Franco-Lopez, H.; Ek, A.R.; Bauer, M.E. Estimation and mapping of forest stand density, volume, and cover type using the k-nearest neighbors method. Remote Sens. Environ. 2001, 77, 251–274. [Google Scholar] [CrossRef]
- Rajaniemi, S.; Tomppo, E.; Ruokolainen, K.; Tuomisto, H. Estimating and mapping pteridophyte and Melastomataceae species richness in western Amazonian rainforests. Int. J. Remote Sens. 2005, 26, 475–493. [Google Scholar] [CrossRef]
- Liang, S.L.; Li, X.W.; Wang, J.D. Quantitative Remote Sensing: Concepts and Algorithms; Science Press: Beijing, China, 2013. [Google Scholar]
- Moore, A.W.; Lee, M.S. Efficient algorithms for minimizing cross validation error. In Proceedings of the Eleventh International Conference on Machine Learning, New Brunswick, NJ, USA, 10–13 July 1994; pp. 190–198.
- Ji, L.; Wylie, B.K.; Nossov, D.R.; Peterson, B.; Waldrop, M.P.; McFarland, J.W.; Rover, J.; Hollingsworth, T.N. Estimating aboveground biomass in interior Alaska with Landsat data and field measurements. Int. J. Appl. Earth Observ. Geoinf. 2012, 18, 451–461. [Google Scholar] [CrossRef]
- Clevers, J.; van der Heijden, G.; Verzakov, S.; Schaepman, M. Estimating grassland biomass using SVM band shaving of hyperspectral data. Photogr. Eng. Remote Sens. 2007, 73, 1141–1148. [Google Scholar] [CrossRef]
- Kajisa, T.; Murakami, T.; Mizoue, N.; Top, N.; Yoshida, S. Object-based forest biomass estimation using Landsat ETM+ in Kampong Thom Province, Cambodia. J. For. Res. 2009, 14, 203–211. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.; Batistella, M.; Zhang, M.; Laurin, G.V.; Saah, D. Aboveground forest biomass estimation with Landsat and Lidar data and uncertainty analysis of the estimates. Int. J. For. Res. 2012, 2012, 436537. [Google Scholar] [CrossRef]
- Timothy, D.; Onisimo, M.; Cletah, S.; Adelabu, S.; Tsitsi, B. Remote sensing of aboveground forest biomass: A review. Trop. Ecol. 2016, 57, 125–132. [Google Scholar]
- Nelson, R.F.; Kimes, D.S.; Salas, W.A.; Routhier, M. Secondary forest age and tropical forest biomass estimation using thematic mapper imagery. BioScience 2000, 50, 419–431. [Google Scholar] [CrossRef]
- Foody, G.M.; Boyd, D.S.; Cutler, M.E. Predictive relations of tropical forest biomass from Landsat TM data and their transferability between regions. Remote Sens. Environ. 2003, 85, 463–474. [Google Scholar] [CrossRef]
- Zheng, D.; Rademacher, J.; Chen, J.; Crow, T.; Bresee, M.; Le Moine, J.; Ryu, S.R. Estimating aboveground biomass using Landsat 7 ETM+ data across a managed landscape in northern Wisconsin, USA. Remote Sens. Environ. 2004, 93, 402–411. [Google Scholar] [CrossRef]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Zhao, P.; Lu, D.; Wang, G.; Wu, C.; Huang, Y.; Yu, S. Examining spectral reflectance saturation in Landsat imagery and corresponding solutions to improve forest aboveground biomass estimation. Remote Sens. 2016. [Google Scholar] [CrossRef]
- Fassnacht, K.S.; Gower, S.T.; MacKenzie, M.D.; Nordheim, E.V.; Lillesand, T.M. Estimating the leaf area index of North Central Wisconsin forests using the landsat thematic mapper. Remote Sens. Environ. 1997, 61, 229–245. [Google Scholar] [CrossRef]
- Jakubauskas, M.E. Thematic Mapper characterization of lodgepole pine seral stages in Yellowstone National Park, USA. Remote Sens. Environ. 1996, 56, 118–132. [Google Scholar] [CrossRef]
- Steininger, M.K. Satellite estimation of tropical secondary forest above-ground biomass: Data from Brazil and Bolivia. Int. J. Remote Sens. 2000, 21, 1139–1157. [Google Scholar] [CrossRef]
- Jiao, X.M.; Xiang, W.H.; Tian, D.L. Carbon Storage of Forest Vegetation and Its Geographical Distribution in Hunan Province. J. Cent. South For. Univ. 2005, 25, 4–8. (In Chinese) [Google Scholar]
- Liu, C.; Liu, M.; Wang, K.L.; Chen, H.S. Evolvement of landscape pattern in upper and middle reaches of Xiangjiang River. Chin. J. Ecol. 2007, 26, 1822–1827. (In Chinese) [Google Scholar]
- Huang, X.N.; Tong, J. Dynamics of carbon storage of Chinese fir in Hunan province. J. Cent. South Univ. For. Technol. 2011, 31, 80–84. (In Chinese) [Google Scholar]
- Xu, X.; Yang, D. Spatial distribution and dynamic changes of total biomass quantity of Pinus massoniana forests in Hunan province. J. Cent. South Univ. For. Technol. 2012, 32, 73–78. [Google Scholar]
- Jiang, Y.T. Analysis of Spatio-Temporal Dynamics and Factors Influencing Vegetation NPP in Xiangjiang River Basin. Master’s Thesis, Hunan University of Science and Technology, Xiangtan, China, May 2015. [Google Scholar]
- Liu, Z.D.; Li, B.; Fang, X.; Xiang, W.H.; Tian, D.L.; Yan, W.D.; Lei, P.F. Dynamic characteristics of forest carbon storage and carbon density in Hunan Province. Acta Ecol. Sin. 2016, 36, 6897–6908. [Google Scholar]
- Wang, X.; Feng, Z.; Ouyang, Z. Vegetation carbon storage and density of forest ecosystems in China. Chin. J. Appl. Ecol. 2001, 12, 13–16. (In Chinese) [Google Scholar]
- Chave, J.; Condit, R.; Aguilar, S.; Hernandez, A.; Lao, S.; Perez, R. Error propagation and scaling for tropical forest biomass estimates. Phil. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 409–420. [Google Scholar] [CrossRef] [PubMed]
- Ledo, A.; Cornulier, T.; Illian, J.B.; Iida, Y.; Kassim, A.R.; Burslem, D.F. Re-evaluation of individual diameter: Height allometric models to improve biomass estimation of tropical trees. Ecol. Appl. 2016, 26, 2374–2380. [Google Scholar] [CrossRef] [PubMed]
- Réjou-Méchain, M.; Muller-Landau, H.C.; Detto, M.; Thomas, S.C.; Le Toan, T.; Saatchi, S.S.; Barreto-Silva, J.S.; Bourg, N.A.; Bunyavejchewin, S.; Butt, N.A.; et al. Local spatial structure of forest biomass and its consequences for remote sensing of carbon stocks. Biogeoscience 2014, 11, 6827–6840. [Google Scholar] [CrossRef] [Green Version]
- Milena, S.; Markku, K. Allometric models for tree volume and total aboveground biomass in a tropical humid forest in Costa Rica. Biotropica 2005, 37, 2–8. [Google Scholar]
- Miyakuni, K.; Heriansyah, I.; Heriyanto, N.M.; Kiyono, Y. Allometric biomass equations, biomass expansion factors and root-to-shoot ratios of planted Acacia mangium Willd. Forests in West Java, Indonesia. J. Forest Plan. 2004, 10, 69–76. [Google Scholar]
- Stegen, J.C.; Swenson, N.G.; Valencia, R.; Enquist, B.J.; Thompson, J. Above-ground forest biomass is not consistently related to wood density in tropical forests. Glob. Ecol. Biogeogr. 2009, 18, 617–625. [Google Scholar] [CrossRef]






| Approach | Mean AGB (Mg/ha) | R2 | RMSE (Mg/ha) | (Mg/ha) | (Mg/ha) | |
|---|---|---|---|---|---|---|
| FID | 64.53 | — | — | — | — | |
| MLR | 64.51 | 0.54 | 31.55 | 60.31 | 1.30 | |
| LR | 64.52 | 0.52 | 32.43 | 59.11 | 1.35 | |
| g-kNN | k = 3 | 64.46 | 0.48 | 34.78 | 60.24 | 1.56 |
| k = 5 | 64.01 | 0.51 | 32.90 | 59.74 | 1.39 | |
| k = 7 | 63.90 | 0.53 | 32.14 | 59.55 | 1.33 | |
| k = 10 | 63.84 | 0.54 | 31.87 | 59.32 | 1.31 | |
| CW-kNN | k = 3 | 63.94 | 0.48 | 34.66 | 59.74 | 1.55 |
| k = 5 | 64.07 | 0.51 | 32.95 | 59.88 | 1.40 | |
| k = 7 | 63.98 | 0.53 | 32.36 | 59.69 | 1.35 | |
| k = 10 | 63.88 | 0.54 | 31.93 | 59.47 | 1.31 | |
| Interval | FID | MLR | LR | g-kNN | CW-kNN | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Mg/ha) | k = 3 | k = 5 | k = 7 | k = 10 | k = 3 | k = 5 | k = 7 | k = 10 | |||
| <0 | 0.00 | 5.79 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 0~1 | 3.60 | 0.00 | 0.01 | 1.00 | 0.92 | 0.93 | 0.89 | 1.00 | 0.91 | 0.92 | 0.89 |
| 1~20 | 22.60 | 7.33 | 15.62 | 23.50 | 22.16 | 21.90 | 22.47 | 23.81 | 22.29 | 22.08 | 22.69 |
| 20~40 | 4.80 | 14.47 | 19.35 | 7.71 | 9.93 | 10.49 | 10.10 | 7.35 | 9.90 | 10.42 | 9.80 |
| 40~60 | 14.80 | 18.17 | 16.19 | 12.37 | 9.57 | 7.88 | 7.05 | 12.02 | 9.03 | 7.40 | 6.50 |
| 60~80 | 18.50 | 25.50 | 19.02 | 20.77 | 21.30 | 21.42 | 21.18 | 20.98 | 21.18 | 21.17 | 21.38 |
| 80~100 | 13.70 | 23.64 | 17.30 | 20.74 | 25.22 | 28.03 | 30.91 | 21.10 | 25.81 | 28.74 | 31.43 |
| 100~120 | 10.20 | 4.99 | 10.09 | 9.75 | 8.61 | 8.06 | 6.72 | 9.58 | 8.69 | 8.08 | 6.65 |
| 120~140 | 6.00 | 0.11 | 2.28 | 2.94 | 1.90 | 1.04 | 0.62 | 2.95 | 1.81 | 0.99 | 0.60 |
| 140~220 | 5.80 | 0.03 | 0.15 | 1.21 | 0.39 | 0.25 | 0.07 | 1.20 | 0.39 | 0.21 | 0.05 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Huang, Z.; Sun, H.; Wang, G. Mapping Forest Ecosystem Biomass Density for Xiangjiang River Basin by Combining Plot and Remote Sensing Data and Comparing Spatial Extrapolation Methods. Remote Sens. 2017, 9, 241. https://doi.org/10.3390/rs9030241
Zhu J, Huang Z, Sun H, Wang G. Mapping Forest Ecosystem Biomass Density for Xiangjiang River Basin by Combining Plot and Remote Sensing Data and Comparing Spatial Extrapolation Methods. Remote Sensing. 2017; 9(3):241. https://doi.org/10.3390/rs9030241
Chicago/Turabian StyleZhu, Jia, Zhihong Huang, Hua Sun, and Guangxing Wang. 2017. "Mapping Forest Ecosystem Biomass Density for Xiangjiang River Basin by Combining Plot and Remote Sensing Data and Comparing Spatial Extrapolation Methods" Remote Sensing 9, no. 3: 241. https://doi.org/10.3390/rs9030241
APA StyleZhu, J., Huang, Z., Sun, H., & Wang, G. (2017). Mapping Forest Ecosystem Biomass Density for Xiangjiang River Basin by Combining Plot and Remote Sensing Data and Comparing Spatial Extrapolation Methods. Remote Sensing, 9(3), 241. https://doi.org/10.3390/rs9030241