1. Introduction
Aerial imagery, including that from unmanned aerial vehicles (UAVs), has become increasingly popular. Its advantages, such as high spatial resolution, low cost, and ready availability, provide numerous potential applications [
1,
2,
3]. Compared with low or median spatial resolution images, aerial images often have very high spatial resolution (VHSR). This provides more details of the earth surface, including the shape, structure, size, and texture of ground targets, and even topology and thematic information among targets. Therefore, a VHSR image is useful for investigating urban environments, target extraction, and urban land-cover mapping [
4,
5,
6,
7]. However, the higher resolution does not necessarily produce greater classification accuracies; VHSR image classification poses a challenge in practical application [
8]. This is because if the spatial resolution is very fine, then the classification could not be improved anymore because of the within-class variability in spectral values. To conquer this problem, spatial feature extraction and complementing with spectral features are known to be important technique in VHSR image classification [
9].
Spatial feature extraction is aimed at describing the shape, structure, and size of a target on the earth surface. However, the spatial arrangement of the ground targets is complex and uncertain. Many researchers have proposed threshold-based approaches to extract spatial features and improve the performance of VHSR image classification. For example, Han et al. considered the shape and size of a homogeneous area, selecting suitable spatial features using parameters [
10]. Zhang et al. discussed a multiple shape feature set that can characterize the target using different points to enhance classification accuracy [
11]. However, an “optimal” threshold for a given image cannot be determined until a series of experiments has been carried out, which is very time-consuming. Although such a threshold can be selected by experiment, one cannot know whether it is indeed the best for all images. Furthermore, such a single optimal threshold may not handle the various shapes in all image cases.
Besides threshold-based extension methods, a mathematical model is an effective means to treat contextual information for extracting spatial features. For example, Moser et al. extracted spatial-contextual information using the Markov random field (MRF) [
12]. There is extensive literature on the use of MRF in VHSR image classification, such as [
13,
14,
15]. Morphological profiles (MPs) represent another powerful tool for spatial feature extraction [
16]. The structural element (SE) is crucial to morphological operations, so MPs have been extended in size and shape by many researchers [
9,
17]. Furthermore, MP attributes have been exploited for describing spatial features of VHSR images [
18,
19,
20]. Among these methods, contextual information within a “window” around a central pixel is simulated and a mathematical model extracted, such as the MRF or MPs. However, the main limitations of considering a set of neighbors using a regular window are the following: (i) The regular neighborhood may not cover the various shapes of different targets in the varying classes, or even different targets within a single class; (ii) although extension of the MP in size or shape can improve the classification performance, it is still inadequate to fit the various shapes and sizes of ground targets in an image scene. Therefore, the adaptive ability of a spatial feature extraction approach should be studied extensively. Ideally, spatial feature extraction should be driven by the image data itself.
In recent decades, many literature works have revealed that image object-based image analysis was effective for that classification [
21,
22]. An image object is a group pixel set with similar spectral values, such that the object has homogeneous spectra. Compared with pixel-based methods, the object-based approach has two advantages: (i) Image objects have more usable features (e.g., shape, size and texture) than a single pixel; (ii) because the processing unit is improved from pixel to object, much “salt and pepper” noise can be smoothed in the classification results. For example, Zhao et al. proposed an algorithm integrating spectral, spatial contextual, and spatial location cues within a condition random field framework to improve the performance of VHSR image classification [
23]. Zhang et al. proposed an object-based spatial feature called object correlative index (OCI) to improve land-cover classification [
24]. Most of image object-based classification methods rely on the performance of segmentation [
25]. However, the scale parameter of multi-resolution segmentation is difficult to determine [
26]. In the present work, we integrated an image raster and its corresponding segment vector to use topological relationships and geographic characteristics, with the aim of extracting VHSR image spatial features automatically.
The proposed approach is based on two simple assumptions: (i) Objects making up a target are not only spatially continuous but are also more homogeneous in spectra than objects not belonging to the same target; (ii) objects from one target usually have very similar auto-correlation. As shown in
Figure 1, objects comprising a ground target appear spectrally very similar, and are continuous in the spatial domain. Based on this observation, Tobler’s First Law of Geography (TFL) of geographic and topologic relationships of an object is used to constrain the extension for exploring the target region. One advantage of this combination is that it can better model the spatial arrangement of a target and effectively detect the target regardless of its shape or size (e.g., the rectangular or “L” shaped building or linear road in
Figure 1). For the second assumption above (ii), Moran’s Index (MI) is typically used to quantitatively measure auto-correlation of the pixels for an object. Then, objects making up a target with similar (homonymous) MI are used to constrain the extension. In other words, the extension of a region for an uncertain target should be driven by the TFL of geography and the target itself, rather than parameter constraints. Experimental results demonstrate outstanding classification accuracy performance of the proposed feature extraction method. This means that the two basic assumptions based on observation of the ground target’s geography are very useful in feature extraction of VHSR aerial imagery.
The main goal of this paper was to propose an automatic object-based, spatial-spectral feature extraction method for VHSR image classification. With the aid of TFL of geography, that method extracts spatial features based on topology and spectral feature constraints, which are important to VHSR image classification. In more detail, the contributions of the method are as follows:
- (i)
Contextual information of remote sensing imagery has been studied extensively and TFL has been widely applied in the field of geographic information systems (GIS). However, to the best of our knowledge, few approaches have been developed based on the TFL of geography for VHSR image classification in an object-manner. The present study proves that GIS spatial analysis can be used effectively for spatial feature extraction of VHSR images.
- (ii)
When an image is processed by multi-scale segmentation, the topological relationship between a central object and surrounding objects becomes more complex, unlike a central pixel and its neighboring pixels (e.g., 4-connectivity or 8-connectivity). Another contribution of this study is its extension strategy based on topology and spectral feature constraints, which is adaptive and improves modeling of the shape and size of an uncertain target.
- (iii)
Besides the segmentation, the progress of feature extraction is automatic, and no parameter adjustment is necessary during its application to classification. This opens up the possibility of widespread practical application to remote sensing imagery.
The remainder of this paper is organized as follows. In
Section 2, TFL of geography is reviewed. In
Section 3, the proposed feature extraction method is described. An experimental description is given in
Section 4 and conclusions are given in
Section 5.
2. Review of Tobler’s First Law of Geography
Here, we briefly review TFL. According to Waldo Tobler, the first law of geography is that “everything is related to everything else, but near things are more related than distant things” [
27]. It is evident from this law that it was largely ignored and the quantitative revolution declined, but it gained prominence with the growth of GIS. Despite notable exceptions, it is hard to imagine a world in which the law is not true, and it provides a very useful principle for analyzing earth surface information [
28]. The widespread application of geography today accommodates a variety of perspectives on the significance of this law [
29,
30]. Remote sensing imagery is obtained based on the radiance of specific source targets on the ground surface. Therefore, when an image is segmented into objects, those objects are related in the spatial and spectral domains. Thus, TFL of geography is applicable to image analysis.
To extract spatial features of images based on TFL of geography, it is necessary to quantitatively measure correlation among objects and pixels within an object. The MI, an index of spatial dependence, is common for specifically describing metrics of spatial autocorrelation. MI has positive values when TFL applies, is zero when neighboring values are as different as distant ones, and is negative when neighboring values are more different than distant ones [
31]. MI of object
o is defined in Equation (1), where
is given in Equation (2).
Here, b is the band index of the image and n is the total number of bands. N is the total number of pixels within the object. is a pixel value of band b within o. is an element of a matrix of spatial weights; if xi and xj are neighbors, , otherwise . is the mean of pixels within o.
The constraint-rule on the extension around a central object is analyzed further in
Section 3. In particular, we had two objectives: (i) TFL of geography is introduced for spatial feature extraction of a VHSR image, and its feasibility investigated; (ii) to reduce the classification algorithm’s data dependence and expand application of the VHSR image, we advance a “rule-constraint” automatic feature extraction method based on TFL of geography, instead of the traditional parameter-based feature extraction approach. One important difference between TFL in our study and spatial contextual information related in existing approaches is that TFL is adopted as a “relaxing rule” in the description of neighboring information, while many existing approaches describe the spatial contextual information in a rigorous manner. In addition, the relaxing rule in our study is driven adaptively by the contextual information rather than by a preset parameter. Details of our proposed methods are presented in
Section 3.
3. Proposed Approach
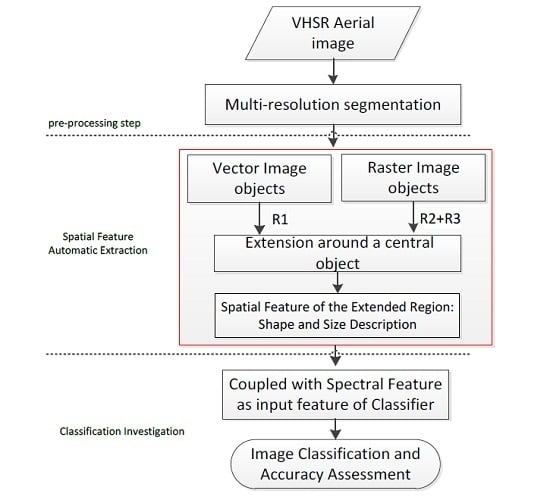
The proposed approach contains three main-blocks, as shown in
Figure 2, they are: (1)
Pre-processing step: In this paper, spatial features of a VHSR image are extracted in an object-by-object manner. Thus, image objects are first extracted using multi-resolution segmentation approach, which is embedded in the well-known eCogintion software [
32]. The multi-resolution segmentation is an iterative region and bottom-up merging segmentation approach, and the merging process relies on local homogeneity by comparing adjacent objects within a certain radius [
33]; (2)
Spatial Feature Automatic Extraction: After segmentation, each image object is scanned and processed by an iterative procedure, as labeled by the red rectangle in
Figure 2. The algorithm for the extension and spatial features for an extended region are described in the following sub-sections; (3)
Classification Investigation: To test the accuracy and feasibility of the proposed automatic feature extraction approach, the proposed approach is compared with different spatial feature extraction approaches through land cover classification. Due to this, the concentration of this paper is to propose an automatic spatial feature extraction approach, the second block (spatial feature automatic extraction) will be detailed in the following sub-sections.
3.1. Extension Based on Constraint of TFL of Geography
Based on the segmentation results, a target may be composed of a group of correlative objects. Extension from one object of the group is used to extract the target region. However, target shape and size is uncertain in the spatial domain, and the objects in a group may vary spectrally and in homogeneity. Thus, it is difficult to constrain this extension by a determined parameter for a variety of target classes within an image scene. Here, three rules derived from TFL of geography are used to constrain the extension. To clarify this, symbols are explained in
Table 1.
Extension for a specific central object is done in an object manner, given that the following rules are satisfied. Each extension around is an iteration that is terminated depending on whether the relationship between and meets the following rules of constraint.
R1: and touch each other directly or indirectly in topology. “Indirectly” means that a connection has been built by previous extension between and , but without direct touching.
R2: is in the range
R3: should meet the constraint or . In other words, not only should and both have positive or negative MIs, but the explored region constructed by the extended objects should realize positive or negative MIs with its candidate component object .
The details of these constraints used to explore the target region are shown in Algorithm 1 and
Figure 3.
| Algorithm 1. Extension of an object |
| Input: One of the segmented image object, . |
| Output: A group of object sets that are surrounded :. |
- 1.
In the initialization step, is added to . - 2.
An object that touches in topology is collected in a container, which is designated by ;. - 3.
A feature vector () is built, based on mean values of band-1, band-2, band-3 and brightness of , and () is prepared for each object of . The distance between and is compared, and the nearest-neighbor object is selected from . - 4.
If and meet the constrained rule R1, R2, and R3, is accepted as the “same-target-source” object while compared with ; 4.1. is added to . At the same time, is used to replace for extension. 4.2. From step-1 through to step-4.1 is an iterative procedure. The iterative extension terminates when any of the three constraint rules is not satisfied. - 5.
Else, terminate the extension and return .
|
- 6.
Extension end.
|
It should be noted that: (i) In each iteration,
is replaced only for the extension in the spatial domain. The initial attribute of
, including its mean and standard deviation, are not varied in step-3 and the constraint rule (R2 and R3); (ii) according to TLF of geography, an object within the surrounding object set that achieves the nearest distance between itself and its central object is selected as the next central object for iteration, and distances are determined by (3). This is to ensure that the explored objects produce features similar to the central object
in the attribute (feature) domain, but extend one by one in the spatial domain. As an example, in
Figure 3,
is highlighted as the central object, and it is readily seen that the region of a target soil can be extracted object-by-object using our proposed algorithm.
where
is the distance between the two vectors
and
,
is o’s feature vector,
,
is the mean value for band-1 pixels within o, and
is the brightness of o. As with
,
.
The segmented vector is exported with the mean of the RGB band and brightnesses to a shape file. The vector layer is overlaid by the image raster for spatial analysis by our proposed algorithms. Application of the proposed algorithm was developed with the ESRI ArcGIS Engine 10.1 development kit and C# language.
3.2. Spatial Features: Shape and Size of Exploited Region
When iteration of an extension surrounding a central object is terminated, a homogenous and spatially continuous group of objects is output. To describe spatial features of the region composed by these grouped objects, a shape index (SI) and size-area (SA) are proposed, because shape and size are important for distinguishing various ground objects.
where
is distance between the gravity point (
) and region boundary point
,
n is the total number of points on the region boundary, and n is determined by the interval distance and boundary length, as shown in
Figure 4.
SA is given by
where
a is the image spatial resolution and
is the area of a pixel.
M is the total number of pixels within the extended region.
Each image object is scanned and processed by proposed Algorithm 1. Then, two spatial features, SI and SA, are extracted automatically to complement the spectral features for classification. The proposed method benefits from the following characteristics.
- (i)
The segmented vector and image raster are integrated for spatial feature extraction, thereby demonstrating the novel concept that segmented vectors of topology and image features are both useful and feasible for VHSR image feature extraction.
- (ii)
Three constraints and their related algorithms are driven based on the geographic theory of TFL. The proposed approach is automatic without any parameterization, thereby reducing data dependence and holding the promise of additional applications to VHSR image classification. It is worth noting that “automatic” means the progress of the feature extraction is automatic (excluding the segmentation and the supervised classification).
- (iii)
The proposed approach based on TFL can adaptively extract the region of a target, because the extension around a central object is driven by the spatial contextual information itself.
5. Conclusions
In this work, an automatic object-based, spatial-spectral feature extraction approach was proposed for the classification of VHSR aerial imagery. The proposed approach was inspired by TFL of geography to constrain the extent of region exploration. Two spatial features, SI and SA, are proposed for describing the region until the extension is terminated. Experiments were conducted on three actual VHSR aerial images. The experimental results demonstrate the effectiveness of our approach, which gave results superior to those from the use of only original spectral features, the widely used spatial-spectral method, M-MPs, APs, RFs, RGF, and OCI.
Based on the findings of this work from analysis and experiment, we conclude that, the TFL of geography can be used for quantitative image feature extraction from VHSR imagery, which contains spatial data describing the land cover on the earth surface. Moreover, although the two types of spatial data (raster and vector) are very different in their characteristics, they can be integrated with the aid of intrinsic geography. This is helpful for better modeling of the spatial features of VHSR images.
Furthermore, from the perspective of practical application, the proposed feature extraction approach without a parameter is simple and data-dependent, which will lead to more potential applications. With the development of UAV technology, large numbers of VHSR images can be acquired conveniently, and classification is important in practical application [
37]. Further development of this work will include comprehensive research on the topological relationship between objects. In addition, because the smaller zone that is meaningless compared with the object of interest, and which can be seen as containing “noise objects,” has a negative effect on classification performance and accuracy, knowledge-based rules driven by expert experience will be considered for optimizing the post-classified map.