Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site and Experimental Design
2.2. Data Collection
2.3. Methods
2.3.1. Random Forest Algorithm
2.3.2. Artificial Neural Network Algorithm
2.3.3. Support Vector Machine Algorithm
2.3.4. Partial Least Squares Algorithm
2.3.5. Precision Evaluation
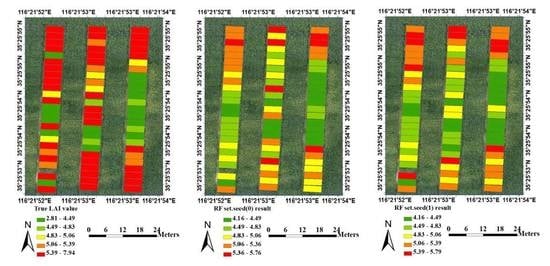
3. Results and Analysis
3.1. Calibration Set and Validation Set Based on Sampling Strategy
3.2. Appropriate Model Parameters for LAI Inversion Model
3.3. Comparison of Whole Growth Period Models
3.4. Comparison of Single Growth Period Models
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lugg, D.G.; Sinclair, T.R. Seasonal changes in photosynthesis of field-grown soybean leaflets. 2. Relation to nitrogen content. Photosynthetica 1981, 15, 138–144. [Google Scholar]
- Burkey, K.O.; Wells, R. Response of soybean photosynthesis and chloroplast membrane function to canopy development and mutual shading. Plant Physiol. 1991, 97, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Boerma, H.R.; Specht, J.E. Soybeans: Improvement, Production and Uses; American Society of Agronomy: Madison, WI, USA, 2004. [Google Scholar]
- Chen, J.M.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.G. Derivation and validation of Canada-wide coarse-resolution leaf area index maps using high-resolution satellite imagery and ground measurements. Remote Sens. Environ. 2002, 80, 165–184. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar] [CrossRef]
- Breda, N. Ground-based measurements of leaf area index: A review of methods, instruments and current controversies. J. Exp. Bot. 2003, 54, 2403–2417. [Google Scholar] [CrossRef] [PubMed]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination—Part I. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Campos-Taberner, M.; Javier Garcia-Haro, F.; Camps-Valls, G.; Grau-Muedra, G.; Nutini, F.; Crema, A.; Boschetti, M. Multitemporal and multiresolution leaf area index retrieval for operational local rice crop monitoring. Remote Sens. Environ. 2016, 187, 102–118. [Google Scholar] [CrossRef]
- Liu, K.; Zhou, Q.; Wu, W.; Xia, T.; Tang, H. Estimating the crop leaf area index using hyperspectral remote sensing. J. Integr. Agric. 2016, 15, 475–491. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Bao, Y.; Luo, J.; Jin, X.; Xu, X.; Song, X.; Yang, G. Exploring the best hyperspectral features for LAI estimation using partial least squares regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef]
- Liang, L.; Di, L.; Zhang, L.; Deng, M.; Qin, Z.; Zhao, S.; Lin, H. Estimation of crop LAI using hyperspectral vegetation indices and a hybrid inversion method. Remote Sens. Environ. 2015, 165, 123–134. [Google Scholar] [CrossRef]
- Fan, W.J.; Xu, X.R.; Liu, X.C.; Yan, B.Y.; Cui, Y.K. Accurate LAI retrieval method based on PROBA/CHRIS data. Hydrol. Earth Syst. Sci. 2010, 14, 1499–1507. [Google Scholar] [CrossRef]
- Delegido, J.; Verrelst, J.; Rivera, J.P.; Ruiz-Verdu, A.; Moreno, J. Brown and green LAI mapping through spectral indices. Int. J. Appl. Earth Obs. 2015, 35, 350–358. [Google Scholar] [CrossRef]
- Vuolo, F.; Dini, L.; D’Urso, G. Retrieval of leaf area index from CHRIS/PROBA data: An analysis of the directional and spectral information content. Int. J. Remote Sens. 2008, 29, 5063–5072. [Google Scholar] [CrossRef]
- Jihua, M.; Bingfang, W.; Qiangzi, L. Method for estimating crop leaf area index of China using remote sensing. Trans. Chin. Soc. Agric. Eng. 2007, 23, 160–167. [Google Scholar]
- Verrelst, J.; Camps-Valls, G.; Munoz-Mari, J.; Pablo Rivera, J.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Liang, D.; Guan, Q.; Huang, W.; Huang, L.; Yang, G. Remote sensing inversion of leaf area index based on support vector machine regression in winter wheat. Trans. Chin. Soc. Agric. Eng. 2013, 29, 117–123. [Google Scholar]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote Sens. Environ. 2004, 92, 195–206. [Google Scholar] [CrossRef]
- Duan, S.; Li, Z.; Wu, H.; Tang, B.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. Int. J. Appl. Earth Obs. 2014, 26, 12–20. [Google Scholar] [CrossRef]
- Herrmann, I.; Pimstein, A.; Karnieli, A.; Cohen, Y.; Alchanatis, V.; Bonfil, D.J. LAI assessment of wheat and potato crops by VENμS and Sentinel-2 bands. Remote Sens. Environ. 2011, 115, 2141–2151. [Google Scholar] [CrossRef]
- Megainduction, J.C. Machine Leaming on Very Large Database; School of Computer Science, University of Technology: Sydney, Australia, 1991. [Google Scholar]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
- Han, Z.Y.; Zhu, X.C.; Fang, X.Y.; Wang, Z.Y.; Wang, L.; Zhao, G.X.; Jiang, Y.M. Hyperspectral estimation of apple tree canopy LAI based on SVM and RF regression. Spectrosc. Spectr. Anal. 2016, 36, 800–805. [Google Scholar]
- Omer, G.; Mutanga, O.; Abdel-Rahman, E.M.; Adam, E. Empirical prediction of Leaf Area Index (LAI) of endangered tree species in intact and fragmented indigenous forests Ecosystems using WorldView-2 data and two robust machine learning algorithms. Remote Sens. 2016, 8, 324. [Google Scholar] [CrossRef]
- Verrelst, J.; Munoz, J.; Alonso, L.; Delegido, J.; Pablo Rivera, J.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ. 2012, 118, 127–139. [Google Scholar] [CrossRef]
- Mustafa, Y.T.; Van Laake, P.E.; Stein, A. Bayesian network modeling for improving forest growth estimates. IEEE Trans. Geosci. Remote 2011, 49, 639–649. [Google Scholar] [CrossRef]
- Bo, Q.I.; Zhang, N.; Zhao, T.J.; Xing, G.N.; Zhao, J.M.; Gai, J.Y. Prediction of leaf area index using hyperspectral remote sensing in breeding programs of soybean. Acta Agron. Sin. 2015, 41, 1073. [Google Scholar]
- Wong, T. Parametric methods for comparing the performance of two classification algorithms evaluated by k-fold cross validation on multiple data sets. Pattern Recogn. 2017, 65, 97–107. [Google Scholar] [CrossRef]
- Mingliang, L.I.; Yang, D.; Chen, J. Probabilistic flood forecasting by a sampling-based Bayesian model. J. Hydroelectr. Eng. 2011, 30, 27–33. [Google Scholar]
- Cochran, W.G. Sampling Technique; China Statistical Publishing House: Beijing, China, 1985. [Google Scholar]
- Aasen, H.; Burkart, A.; Bolten, A.; Bareth, G. Generating 3D hyperspectral information with lightweight UAV snapshot cameras for vegetation monitoring: From camera calibration to quality assurance. ISPRS J. Photogramm. 2015, 108, 245–259. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J.; Tang, H.; Huang, C.; Yang, F.; Chen, B.; Wang, X.; Xin, X.; Ge, Y. Predicting grassland leaf area index in the Meadow Steppes of Northern China: A comparative study of regression approaches and hybrid geostatistical methods. Remote Sens. 2016, 8, 632. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, C.; Huang, W. Foundations and Applications of Quantitative Remote Sensing in Agriculture, 1st ed.; Science Press: Beijing, China, 2008; pp. 156–157. [Google Scholar]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ. 1990, 33, 55–64. [Google Scholar] [CrossRef]
- Frigge, M.; Hoaglin, D.C.; Iglewicz, B. Some implementations of the boxplot. Am. Stat. 1989, 43, 50–54. [Google Scholar] [CrossRef]
- Benjamini, Y. Opening the box of a boxplot. Am. Stat. 1988, 42, 257–262. [Google Scholar] [CrossRef]
- Cheng, T.; Riaño, D.; Koltunov, A.; Whiting, M.L.; Ustin, S.L.; Rodriguez, J. Detection of diurnal variation in orchard canopy water content using MODIS/ASTER Airborne Simulator (MASTER) data. Remote Sens. Environ. 2013, 132, 1–12. [Google Scholar] [CrossRef]
- Sandelowski, M. Sample size in qualitative research. Res. Nurs. Health 1995, 18, 179–183. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Krishnan, P.; Alexander, J.D.; Butler, B.J.; Hummel, J.W. Reflectance technique for predicting soil organic matter. Soil Sci. Soc. Am. J. 1980, 44, 1282–1285. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- He, Q. Neural Network and its Application in IR; Graduate School of Library and Information Science, University of Illinois at Urbana-Champaign Spring: Champaign, IL, USA, 1999. [Google Scholar]
- Kimes, D.S.; Nelson, R.F.; Manry, M.T.; Fung, A.K. Review article: Attributes of neural networks for extracting continuous vegetation variables from optical and radar measurements. Int. J. Remote Sens. 1998, 19, 2639–2663. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2011. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; Volume 1. [Google Scholar]
- Si, W.; Amari, S.I. Conformal transformation of Kernel functions: A data-dependent way to improve support vector machine classifiers. Neural Process. Lett. 2002, 15, 59–67. [Google Scholar]
- Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A. The R Project for Statistical Computing. Available online: http://www.r-project.org (accessed on 6 April 2005).
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Geisser, S. A predictive approach to the random effect model. Biometrika 1974, 61, 101–107. [Google Scholar] [CrossRef]
- Wolter, P.T.; Townsend, P.A.; Sturtevant, B.R.; Kingdon, C.C. Remote sensing of the distribution and abundance of host species for spruce budworm in Northern Minnesota and Ontario. Remote Sens. Environ. 2008, 112, 3971–3982. [Google Scholar] [CrossRef]
- Mevik, B.; Wehrens, R. The pls package: Principal component and partial least squares regression in R. J. Stat. Softw. 2007, 18, 1–24. [Google Scholar] [CrossRef]
- Tedeschi, L.O. Assessment of the adequacy of mathematical models. Agric. Syst. 2006, 89, 225–247. [Google Scholar] [CrossRef]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G.; Tuv, E. Bias of importance measures for multi-valued attributes and solutions. In Proceedings of the International Conference on Artificial Neural Networks, Espoo, Finland, 14–17 June 2011; pp. 293–300. [Google Scholar]






| Growing Period | Observation Plots | Max Value | Min Value | Mean Value | p Value | Coefficient of Variation |
|---|---|---|---|---|---|---|
| R1 period | 96 | 5.705 | 1.285 | 2.988 | 0.000 | 0.331 |
| R3 period | 126 | 9.06 | 5.415 | 7.295 | 0.051 * | 0.116 |
| R5 period | 123 | 8.22 | 3.15 | 5.479 | 0.002 | 0.197 |
| R6 period | 116 | 6.54 | 1.83 | 4.24 | 0.192 * | 0.262 |
| R7 period | 82 | 6.78 | 1.585 | 3.579 | 0.000 | 0.345 |
| R1~R7 period | 543 | 9.06 | 1.285 | 4.906 | 0.000 | 0.382 |
| RF Regression Model Parameters | |||||||||
| Growth Period | Ntree | mtry | Norm.votes | Reference | |||||
| whole growth period | 500 | 2 | TRUE | Liang et al. [11] | |||||
| single growth period | 500 | 2 | TRUE | ||||||
| ANN Regression Model Parameters | |||||||||
| Weight | Size | Decay | Maxit | Switch for entropy | |||||
| whole growth period | 1 | 1 | 0.001 | 1000 | Least squares | Li et al. [32] | |||
| single growth period | 1 | 1 | 0.0005 | 1000 | Least squares | ||||
| SVM Regression Model Parameters | |||||||||
| Shrinking | Gamma | Eps | C | kernel | Probability | ||||
| whole growth period | 1 | 0.001 | 0.01 | 1 | radial basis | 1 | Li et al. [32] | ||
| single growth period | 1 | 0.01 | 0.01 | 1 | radial basis | 1 | |||
| PLS Regression Model Parameters | |||||||||
| Ncomp | Validation | ||||||||
| whole growth period | 5 | cross-validation (CV) | Li et al. [32] | ||||||
| single growth period | 5 | cross-validation (CV) | |||||||
| Regression Method | V-R2 | V-RMSE | |||
|---|---|---|---|---|---|
| R2 | SDR2 | RMSE | SDRMSE | ||
| SRS | RF | 0.712 | 0.042 | 0.106 | 0.007 |
| ANN | 0.674 | 0.044 | 0.11 | 0.006 | |
| SVM | 0.718 | 0.040 | 0.102 | 0.006 | |
| PLS | 0.657 | 0.041 | 0.114 | 0.006 | |
| STR | RF | 0.741 | 0.031 | 0.106 | 0.005 |
| ANN | 0.706 | 0.036 | 0.11 | 0.006 | |
| SVM | 0.749 | 0.025 | 0.104 | 0.005 | |
| PLS | 0.689 | 0.033 | 0.114 | 0.006 | |
| Regression Method | V-R2 | V-RMSE | |||
|---|---|---|---|---|---|
| R2 | SDR2 | RMSE | SDRMSE | ||
| SRS | RF | 0.375 | 0.137 | 0.090 | 0.009 |
| ANN | 0.427 | 0.135 | 0.086 | 0.010 | |
| SVM | 0.408 | 0.130 | 0.088 | 0.010 | |
| PLS | 0.274 | 0.109 | 0.104 | 0.012 | |
| STR | RF | 0.400 | 0.130 | 0.088 | 0.009 |
| ANN | 0.452 | 0.132 | 0.086 | 0.009 | |
| SVM | 0.439 | 0.108 | 0.089 | 0.007 | |
| PLS | 0.309 | 0.120 | 0.102 | 0.011 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. https://doi.org/10.3390/rs9040309
Yuan H, Yang G, Li C, Wang Y, Liu J, Yu H, Feng H, Xu B, Zhao X, Yang X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sensing. 2017; 9(4):309. https://doi.org/10.3390/rs9040309
Chicago/Turabian StyleYuan, Huanhuan, Guijun Yang, Changchun Li, Yanjie Wang, Jiangang Liu, Haiyang Yu, Haikuan Feng, Bo Xu, Xiaoqing Zhao, and Xiaodong Yang. 2017. "Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models" Remote Sensing 9, no. 4: 309. https://doi.org/10.3390/rs9040309
APA StyleYuan, H., Yang, G., Li, C., Wang, Y., Liu, J., Yu, H., Feng, H., Xu, B., Zhao, X., & Yang, X. (2017). Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sensing, 9(4), 309. https://doi.org/10.3390/rs9040309