Improving the Impervious Surface Estimation from Hyperspectral Images Using a Spectral-Spatial Feature Sparse Representation and Post-Processing Approach
Abstract
:1. Introduction
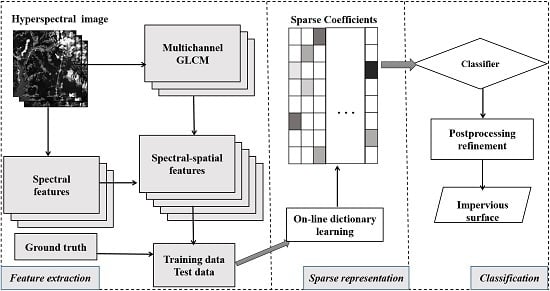
2. Materials and Methods
2.1. Dataset and Preprocessing
2.2. Methods
2.2.1. Feature Extraction
2.2.2. Spectral-Spatial Sparse Representation
2.2.3. Classification Strategy and Accuracy Assessment
3. Results and Analysis
3.1. Experiments with the Hyperion Data
3.2. Experiments with the University of Pavia Image
3.3. Experiments with the Pavia Center Image
3.4. Post-Classification Refinement
4. Discussion
4.1. The Classification Accuracy for Impervious Surface
4.2. The Computational Costs
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Weng, Q. Remote sensing of impervious surfaces in the urban areas: Requirements, methods, and trends. Remote Sens. Environ. 2012, 117, 34–49. [Google Scholar] [CrossRef]
- Fan, F.; Fan, W.; Weng, Q. Improving urban impervious surface mapping by linear spectral mixture analysis and using spectral indices. Can. J. Remote Sens. 2015, 41, 1–10. [Google Scholar] [CrossRef]
- Ma, Q.; He, C.; Wu, J.; Liu, Z.; Zhang, Q.; Sun, Z. Quantifying spatiotemporal patterns of urban impervious surfaces in China: An improved assessment using nighttime light data. Landsc. Urban Plan. 2014, 130, 36–49. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Lin, H. Improving the impervious surface estimation with combined use of optical and sar remote sensing images. Remote Sens. Environ. 2014, 141, 155–167. [Google Scholar] [CrossRef]
- Shao, Z.; Liu, C. The integrated use of DMSP-OLS nighttime light and modis data for monitoring large-scale impervious surface dynamics: A case study in the yangtze river delta. Remote Sens. 2014, 6, 9359–9378. [Google Scholar] [CrossRef]
- Liu, X.; Hu, G.; Ai, B.; Li, X.; Shi, Q. A normalized urban areas composite index (NUACI) based on combination of DMSP-Ols and MODIS for mapping impervious surface area. Remote Sens. 2015, 7, 17168–17189. [Google Scholar] [CrossRef]
- Jing, W.; Yang, Y.; Yue, X.; Zhao, X. Mapping urban areas with integration of DMSP/OLS nighttime light and MODIS data using machine learning techniques. Remote Sens. 2015, 7, 12419–12439. [Google Scholar] [CrossRef]
- Zhou, Y.; Smith, S.J.; Elvidge, C.D.; Zhao, K.; Thomson, A.; Imhoff, M. A cluster-based method to map urban area from DMSP/OLS nightlights. Remote Sens. Environ. 2014, 147, 173–185. [Google Scholar] [CrossRef]
- Wang, Z.; Gang, C.; Li, X.; Chen, Y.; Li, J. Application of a Normalized Difference Impervious Index (NDII) to extract urban impervious surface features based on landsat tm images. Int. J. Remote Sens. 2015, 36, 1055–1069. [Google Scholar] [CrossRef]
- Zhang, L.; Weng, Q. Annual dynamics of impervious surface in the pearl river delta, china, from 1988 to 2013, using time series landsat imagery. ISPRS J. Photogramm. Remote Sens. 2016, 113, 86–96. [Google Scholar] [CrossRef]
- Li, L.; Lu, D.; Kuang, W. Examining urban impervious surface distribution and its dynamic change in Hangzhou metropolis. Remote Sens. 2016, 8, 1–20. [Google Scholar] [CrossRef]
- Song, X.P.; Sexton, J.O.; Huang, C.; Channan, S.; Townshend, J.R. Characterizing the magnitude, timing and duration of urban growth from time series of landsat-based estimates of impervious cover. Remote Sens. Environ. 2016, 175, 1–13. [Google Scholar] [CrossRef]
- Tang, F.; Xu, H.Q. Comparison of performances in retrieving impervious surface between hyperspectral (hyperion) and multispectral (TM/ETM+) images. Spectrosc. Spectr. Anal. 2014, 34, 1075–1080. [Google Scholar]
- Tan, K.; Jin, X.; Du, Q.; Du, P.J. Modified multiple endmember spectral mixture analysis for mapping impervious surfaces in urban environments. J. Appl. Remote Sens. 2014, 8, 085096. [Google Scholar] [CrossRef]
- Shuai, L.; Qi, L. Composite kernel support vector regression model for hyperspectral image impervious surface extraction. J. Remote Sens. 2016, 20, 420–430. [Google Scholar]
- Ridd, M.K. Exploring a vis (vegetation-impervious surface-soil) model for urban ecosystem analysis through remote sensing: Comparative anatomy for cities. Int. J. Remote Sens. 1995, 16, 2165–2185. [Google Scholar] [CrossRef]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sens. Environ. 2003, 84, 493–505. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. A spatially adaptive spectral mixture analysis for mapping subpixel urban impervious surface distribution. Remote Sens. Environ. 2013, 133, 62–70. [Google Scholar] [CrossRef]
- Deng, Y.; Wu, C. Development of a class-based multiple endmember spectral mixture analysis (C-MESMA) approach for analyzing urban environments. Remote Sens. 2016, 8, 349. [Google Scholar] [CrossRef]
- Xu, H. Rule-based impervious surface mapping using high spatial resolution imagery. Int. J. Remote Sens. 2013, 34, 27–44. [Google Scholar] [CrossRef]
- Shao, Z.; Fu, H.; Fu, P.; Yin, L. Mapping urban impervious surface by fusing optical and sar data at the decision level. Remote Sens. 2016, 8, 945. [Google Scholar] [CrossRef]
- Okujeni, A.; van der Linden, S.; Hostert, P. Extending the vegetation-impervious-soil model using simulated enmap data and machine learning. Remote Sens. Environ. 2015, 158, 69–80. [Google Scholar] [CrossRef]
- Weng, Q.; Hu, X.; Lu, D. Extracting impervious surfaces from medium spatial resolution multispectral and hyperspectral imagery: A comparison. Int. J. Remote Sens. 2008, 29, 3209–3232. [Google Scholar] [CrossRef]
- Roberts, D.A.; Gardner, M.; Church, R.; Ustin, S.; Scheer, G.; Green, R.O. Mapping chaparral in the santa monica mountains using multiple endmember spectral mixture models. Remote Sens. Environ. 1998, 65, 267–279. [Google Scholar] [CrossRef]
- Fan, F.; Deng, Y. Enhancing endmember selection in multiple endmember spectral mixture analysis (MESMA) for urban impervious surface area mapping using spectral angle and spectral distance parameters. Int. J. Appl. Earth Obs. 2014, 33, 290–301. [Google Scholar] [CrossRef]
- Van der Linden, S.; Hostert, P. The influence of urban structures on impervious surface maps from airborne hyperspectral data. Remote Sens. Environ. 2009, 113, 2298–2305. [Google Scholar] [CrossRef]
- Fauvel, M.; Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J.; Tilton, J.C. Advances in spectral-spatial classification of hyperspectral images. Proc. IEEE 2013, 101, 652–675. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, H.; Li, Y.; Zhang, Y.; Fang, C. Mapping urban impervious surface with dual-polarimetric sar data: An improved method. Landsc. Urban Plan. 2016, 151, 55–63. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Wei, T.; Zhenwei, S.; Ying, W.; Changshui, Z. Sparse unmixing of hyperspectral data using spectral a priori information. IEEE Trans. Geosci. Remote Sens. 2015, 53, 770–783. [Google Scholar]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A.; Somers, B. Music-csr: Hyperspectral unmixing via multiple signal classification and collaborative sparse regression. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4364–4382. [Google Scholar] [CrossRef]
- Yi, C.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar]
- Du, P.; Xue, Z.; Li, J.; Plaza, A. Learning discriminative sparse representations for hyperspectral image classification. IEEE J. Sel. Top. Signal Process. 2015, 9, 1089–1104. [Google Scholar] [CrossRef]
- Gui, J.; Sun, Z.; Ji, S.; Tao, D.; Tan, T. Feature selection based on structured sparsity: A comprehensive study. IEEE Trans. Neural Netw. Learn. 2016, 25, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Liu, X.; Zhang, L. A multichannel gray level co-occurrence matrix for multi/hyperspectral image texture representation. Remote Sens. 2014, 6, 8424–8445. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C. Updating the 2001 national land cover database impervious surface products to 2006 using landsat imagery change detection methods. Remote Sens. Environ. 2010, 114, 1676–1686. [Google Scholar] [CrossRef]
- Nagel, P.; Yuan, F. High-resolution land cover and impervious surface classifications in the twin cities metropolitan area with naip imagery. Photogramm. Eng. Remote Sens. 2016, 82, 63–71. [Google Scholar] [CrossRef]
- Deng, C. Incorporating endmember variability into linear unmixing of coarse resolution imagery: Mapping large-scale impervious surface abundance using a hierarchically object-based spectral mixture analysis. Remote Sens. 2015, 7, 9205–9229. [Google Scholar] [CrossRef]
- Mairal, J.; Bach, F.; Ponce, J.; Sapiro, G. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 2010, 11, 19–60. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B 1996, 58, 267–288. [Google Scholar]
- Su, H.; Yong, B.; Du, P.; Liu, H.; Chen, C.; Liu, K. Dynamic classifier selection using spectral-spatial information for hyperspectral image classification. J. Appl. Remote Sens. 2014, 8, 085095. [Google Scholar] [CrossRef]
- Li, N.; Bruzzone, L.; Chen, Z.; Liu, F. A novel technique based on the combination of labeled co-occurrence matrix and variogram for the detection of built-up areas in high-resolution sar images. Remote Sens. 2014, 6, 3857–3878. [Google Scholar] [CrossRef]
- Puissant, A.; Hirsch, J.; Weber, C. The utility of texture analysis to improve per-pixel classification for high to very high spatial resolution imagery. Int. J. Remote Sens. 2005, 26, 733–745. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Sun, W.; Jiang, M.; Li, W.; Liu, Y. A symmetric sparse representation based band selection method for hyperspectral imagery classification. Remote Sens. 2016, 8, 238. [Google Scholar] [CrossRef]
- Charles, A.S.; Olshausen, B.A.; Rozell, C.J. Learning sparse codes for hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 963–978. [Google Scholar] [CrossRef]
- Efron, B.; Hastie, T.; Johnstone, I.; Tibshirani, R. Least angle regression. Ann. Stat. 2004, 32, 407–499. [Google Scholar]
- Hu, X.; Weng, Q. Impervious surface area extraction from ikonos imagery using an object-based fuzzy method. Geocarto Int. 2010, 26, 3–20. [Google Scholar] [CrossRef]
- Kotarba, A.Z.; Aleksandrowicz, S. Impervious surface detection with nighttime photography from the international space station. Remote Sens. Environ. 2016, 176, 295–307. [Google Scholar] [CrossRef]
- Li, E.; Du, P.; Samat, A.; Xia, J.; Che, M. An automatic approach for urban land-cover classification from Landsat-8 OLI data. Int. J. Remote Sens. 2015, 36, 5983–6007. [Google Scholar] [CrossRef]
- Samsudin, S.H.; Shafri, H.Z.M.; Hamedianfar, A.; Mansor, S. Spectral feature selection and classification of roofing materials using field spectroscopy data. J. Appl. Remote Sens. 2015, 9, 095079. [Google Scholar] [CrossRef]
- Fernandez, I.; Aguilar, F.J.; Aguilar, M.A.; Flor Alvarez, M. Influence of data source and training size on impervious surface areas classification using vhr satellite and aerial imagery through an object-based approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4681–4691. [Google Scholar] [CrossRef]
- Xu, H.Q.; Wang, M.Y. Remote sensing-based retrieval of ground impervious surfaces. J. Remote Sens. 2016, 20, 1270–1289. [Google Scholar]













| SPE-SVM | SS-SVM | SPE-RF | SS-RF | SPE-SR | SS-SR | |
|---|---|---|---|---|---|---|
| Producer’s Accuracy | 0.513 | 0.534 | 0.599 | 0.633 | 0.573 | 0.636 |
| User’s Accuracy | 0.777 | 0.784 | 0.697 | 0.729 | 0.778 | 0.754 |
| OA | 0.934 | 0.936 | 0.931 | 0.937 | 0.938 | 0.940 |
| AA | 0.748 | 0.759 | 0.784 | 0.803 | 0.777 | 0.806 |
| Kappa | 0.583 | 0.602 | 0.606 | 0.643 | 0.627 | 0.657 |
| SPE-SVM | SS-SVM | SPE-RF | SS-RF | SPE-SR | SS-SR | |
|---|---|---|---|---|---|---|
| Producer’s Accuracy | 0.459 | 0.496 | 0.504 | 0.634 | 0.551 | 0.596 |
| User’s Accuracy | 0.790 | 0.788 | 0.672 | 0.689 | 0.708 | 0.779 |
| OA | 0.952 | 0.954 | 0.946 | 0.953 | 0.951 | 0.957 |
| AA | 0.725 | 0.743 | 0.742 | 0.806 | 0.767 | 0.779 |
| Kappa | 0.557 | 0.585 | 0.548 | 0.635 | 0.594 | 0.637 |
| SPE-SVM | SS-SVM | SPE-RF | SS-RF | SPE-SR | SS-SR | |
|---|---|---|---|---|---|---|
| Producer’s Accuracy | 0.972 | 0.972 | 0.989 | 0.990 | 0.993 | 0.996 |
| User’s Accuracy | 0.993 | 0.996 | 0.981 | 0.992 | 0.983 | 0.993 |
| OA | 0.978 | 0.980 | 0.981 | 0.989 | 0.984 | 0.993 |
| AA | 0.980 | 0.983 | 0.978 | 0.988 | 0.980 | 0.991 |
| Kappa | 0.952 | 0.957 | 0.959 | 0.976 | 0.965 | 0.984 |
| SPE-SVM | SS-SVM | SPE-RF | SS-RF | SPE-SR | SS-SR | |
|---|---|---|---|---|---|---|
| Producer’s Accuracy | 0.911 | 0.910 | 0.985 | 0.989 | 0.989 | 0.990 |
| User’s Accuracy | 0.902 | 0.901 | 0.991 | 0.990 | 0.989 | 0.996 |
| OA | 0.951 | 0.951 | 0.987 | 0.989 | 0.988 | 0.992 |
| AA | 0.956 | 0.955 | 0.987 | 0.989 | 0.988 | 0.992 |
| Kappa | 0.902 | 0.901 | 0.973 | 0.978 | 0.975 | 0.984 |
| OA Kappa (SPE-SVM) | OA Kappa (SS-SVM) | OA Kappa (SPE-RF) | OA Kappa (SS-RF) | OA Kappa (Our Hybrid Approach) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Hyperion dataset 1 | 0.934 | 0.583 | 0.936 | 0.602 | 0.931 | 0.606 | 0.937 | 0.643 | 0.943 | 0.666 |
| Hyperion dataset 2 | 0.952 | 0.557 | 0.953 | 0.585 | 0.946 | 0.548 | 0.953 | 0.635 | 0.958 | 0.640 |
| University of Pavia | 0.978 | 0.952 | 0.980 | 0.957 | 0.981 | 0.959 | 0.989 | 0.976 | 0.996 | 0.992 |
| Pavia center image | 0.951 | 0.902 | 0.951 | 0.901 | 0.987 | 0.973 | 0.989 | 0.978 | 0.993 | 0.987 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Gu, G. Improving the Impervious Surface Estimation from Hyperspectral Images Using a Spectral-Spatial Feature Sparse Representation and Post-Processing Approach. Remote Sens. 2017, 9, 456. https://doi.org/10.3390/rs9050456
Liu S, Gu G. Improving the Impervious Surface Estimation from Hyperspectral Images Using a Spectral-Spatial Feature Sparse Representation and Post-Processing Approach. Remote Sensing. 2017; 9(5):456. https://doi.org/10.3390/rs9050456
Chicago/Turabian StyleLiu, Shuai, and Guanghua Gu. 2017. "Improving the Impervious Surface Estimation from Hyperspectral Images Using a Spectral-Spatial Feature Sparse Representation and Post-Processing Approach" Remote Sensing 9, no. 5: 456. https://doi.org/10.3390/rs9050456
APA StyleLiu, S., & Gu, G. (2017). Improving the Impervious Surface Estimation from Hyperspectral Images Using a Spectral-Spatial Feature Sparse Representation and Post-Processing Approach. Remote Sensing, 9(5), 456. https://doi.org/10.3390/rs9050456