A Machine Learning Based Reconstruction Method for Satellite Remote Sensing of Soil Moisture Images with In Situ Observations

Abstract

Surface soil moisture is an important environment variable that is dominant in a variety of research and application areas. Acquiring spatiotemporal continuous soil moisture observations is therefore of great importance. Weather conditions can contaminate optical remote sensing observations on soil moisture, and the absence of remote sensors causes gaps in regional soil moisture observation time series. Therefore, reconstruction is highly motivated to overcome such contamination and to fill in such gaps. In this paper, we propose a novel image reconstruction algorithm that improved upon the Satellite and In situ sensor Collaborated Reconstruction (SICR) algorithm provided by our previous publication. Taking artificial neural networks as a model, complex and highly variable relationships between in situ observations and remote sensing soil moisture is better projected. With historical data for the network training, feedforward neural networks (FNNs) project in situ soil moisture to remote sensing soil moisture at better performances than conventional models. Consequently, regional soil moisture observations can be reconstructed under full cloud contamination or under a total absence of remote sensors. Experiments confirmed better reconstruction accuracy and precision with this improvement than with SICR. The new algorithm enhances the temporal resolution of high spatial resolution remote sensing regional soil moisture observations with good quality and can benefit multiple soil moisture-based applications and research.

1. Introduction

Surface soil moisture is generally the water content within the upper 10 cm of soil. Although such water is a very small portion of the global water content, it is fundamentally important to many hydrological, biochemical, biological, agricultural and other processes [1]. Many applications also involve surface soil moisture as a key variable, including construction engineering [2], meteorology [3], climate change monitoring [4,5], environmental science [6,7,8] and agricultural modeling [9]. Due to these facts, it is important to monitor soil moisture conditions, especially to obtain spatial and temporal variations in soil moisture.

To acquire as many soil moisture observations as possible with as high a quality as possible, much effort has been applied. On the ground, the international soil moisture network (ISMN) provides a worldwide network of soil moisture in situ observatories [10]. Their discrete observations measure soil moisture only at specific locations and are thus inadequate to represent the soil moisture spatial distribution, although they provide temporally continuous observations. In addition, techniques for measuring soil moisture across a wide area have been developed since the mid–1970s, when a surge in satellite development began. With the development of optical remote sensors onboard satellite missions, more and more optical remote sensing products have been able to provide soil moisture retrieval possibilities. In recent decades, microwave remote sensing has also encountered significant development [11,12,13,14,15]. Specifically, many remote sensing missions have been utilized for soil moisture retrieval. One of the most recent projects is the SMAP-soil moisture active passive mission, which is driven by JPL NASA [16]. Other projects include the moderate resolution imaging spectroradiometer (MODIS) and the Advanced Microwave Scanning Radiometer—EOS (AMSR-E) onboard Aqua [17,18], the Soil Moisture and Ocean Salinity (SMOS) mission driven by the ESA [19].

However, soil moisture remote sensing with microwave techniques is highly dependent on environmental factors such as soil surface roughness [20] and land cover heterogeneity [21]. Although L–band microwave soil moisture products can partially overcome the influence of dense vegetation, optical remote sensing has its advantages in exemption from complicated polarization information exploration or exhaustive field observations on soil surface roughness. Thus, many soil moisture remote sensing achievements have been made on optical soil moisture remote sensing [22,23,24,25,26]. Nevertheless, clouds, thick fogs, mists, darkness, absence of revisiting and many other factors have prevented optical sensors from operating over a required location at the required moment. Although optical remote sensing imaging techniques have achieved massive archives throughout their long history, spatiotemporal gaps of soil moisture observations inevitably exist.

To overcome the incompleteness of soil moisture or other remote sensing results, much elaborative effort has been made. Existing methods can be divided into three categories: (1) methods that fill gaps using spatial information; (2) methods that fill gaps by temporal information; and (3) methods that fill gaps by integrating both spatial and temporal information. In the gap–filling process, some methods also make use of ancillary data sources, such as other remote sensing images, a digital elevation model, or land use state information. Representatives of these categories are listed below.

Table 1. State-of-the-art gap-filling approaches and their shortcomings.

Categories	Approaches	References	Shortcomings
Spatial information based methods	Kriging interpolation	[27,28]	Requires neighborhood information from remote sensing images, which is inaccessible in complete cloud contamination.
	Co-Kriging method	[29,30]
	Co-Kriging method on image segmentations	[31,32,33]
	Neighborhood Similar Pixel Interpolator method	[34,35]
Temporal information based methods	TIMESAT software package	[36]	Natural temporal changes cannot be easily modeled.
	smoothing time-series data	[36]
	Curve fitting on temporal domain	[37]
	Curve fitting and Fourier analysis in frequency domain of time series	[38]
	Phenology models fitting on temporal domain	[39]
Spatiotemporal Combined methods	spatial interpolation in neighborhood before temporal interpolation	[40,41]	Both shortcomings From the spatial approaches and temporal approaches may apply here.
	spatial interpolation in neighborhood after temporal interpolation	[42]
	hybrid Generalized Additive Model	[43]
	Satellite and In-situ sensor Collaborated Reconstruction (SICR)	[44]	Too simple models cannot cover natural relationships and variations.

gives a summary of the state-of-the-art approaches as well as their shortcomings, while detailed comments are farther below.

The first category of methods for filling gaps uses spatial information. Considering the fact that spatially close geospatial features usually appear to be related or similar, geostatistical approaches such as the Kriging method have been widely used in filling gaps of remote sensing images using the information provided by available pixels or auxiliary data around the gaps [27,28]. When another data frame without gaps is available, the co-Kriging method becomes useful to address the extra observations made by the same sensor at the same site on another date to fill gaps in remote sensing images [29,30]. In that case, image segmentations can also be gap-filling units [31,32,33]. Chen et al. [34] also proposed a method that uses data from an alternative date, which is a novel Neighborhood Similar Pixel Interpolator method, to fill gaps for Landsat ETM+ SLC failures. This method was later improved by Zhu et al. [35] using a geostatistical technique.

The second category of methods for filling gaps uses information in time series, specifically the pixel values acquired at moments other than at the gap to be filled. Kandasamy et al. [45] provided an informative review of these temporal methods. Jönsson and Eklundh [36] developed the TIMESAT software package, recovering image gaps by asymmetric Gaussian and Savitzky-Golay filters and smoothing time-series data. Other gap-filling approaches using temporal information include the gap filling on the MODIS Leaf Area Index (LAI) data [37] and AVHRR NDVI data [38]. Later, Verger et al. [39] developed a Consistent Adjustment of the Climatology to Actual Observations approach for increasing the accuracy of temporal interpolations of missing AVHRR LAI data, by utilizing climatological data within the model.

Other than those who utilize either temporal or spatial information for gap filling, there exist several spatiotemporal gap-filling approaches that solve this problem by a combination of temporal and spatial steps. Running et al. [40] provided a method for filling gaps in ecosystem metrics, which include FPAR, LAI, and net photosynthesis. This method on the one hand uses simple spatial interpolation within the same land cover classes. On the other hand, if no cloud-free pixels are available in the neighborhood window of a gap pixel, this method takes temporal interpolation using earlier or later observations. Later, Borak and Jasinski [41] modified this approach to fill gaps on MODIS LAI images over a large portion of North America. Unlike Running et al. [40], Gafurov and Bárdossy [42] developed another algorithm that executes temporal models prior to spatial models. Later, Poggio et al. [43] developed an innovative method for gap-filling MODIS EVI data that utilizes a hybrid Generalized Additive Model (GAM). This geostatistical model uses spatial and temporal information simultaneously.

Overall, the present spatial approaches for filling gaps of remote sensing indices assume access to neighborhood information at the same time, but optical sensors can be totally blocked by heavy fog or thick clouds, which leads to poor spatial information in a single frame of image. In other cases, spaceborne remote sensors without geosynchronous characters could have revisit gaps. These two reasons degrade the capability of such methods. On the other hand, temporal changes of natural variations of environmental metrics might have various characteristics, making the temporal models of other remote sensing metrics incapable of recovering soil moisture.

In [44], a novel method SICR algorithm was proposed to recover soil moisture remote sensing under complete cloud contamination with the help of in situ observations. This innovation study proposed a solution for reconstructing regional soil moisture distributions under complete contamination of a target area in which the optical remote sensors are totally invalid. The SICR algorithm extracts recovery models from historical remotely sensed soil moisture images of the same region, together with contemporary in situ soil moisture observation series by a number of observatories located in this target region.

In this method, linear models were widely utilized. Nevertheless, the relationship between natural factors and remote sensing metrics is not always linear. Moreover, different sensing techniques represent soil moisture at different spatial scales, which are not always linearly related. Therefore, linear models are not adequate for projecting the recovered relationships, and more sophisticated models could be involved.

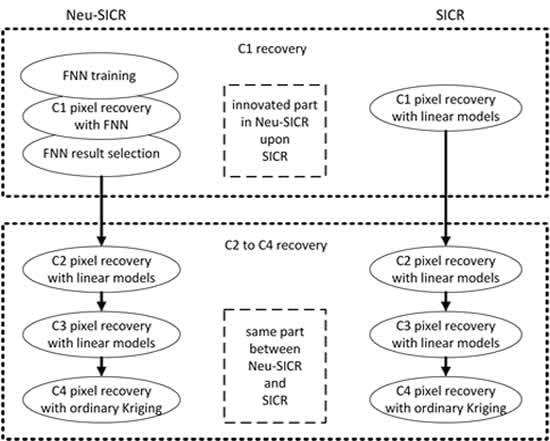
To overcome the aforementioned shortcomings and disadvantages, this paper presents a substitute to one of the recovery models in the SICR method, aiming to improve the recovering accuracy by modeling the projection relationship from in situ soil moisture to remotely sensed soil moisture more accurately. To our knowledge, it is the first approach that utilizes neural network and machine learning techniques for recovering remote sensing soil moisture images while combining spaceborne and in situ data. This approach has improved remotely sensed soil moisture image recovery quality in terms of both accuracy and precision. Benefiting from the flexibility of artificial neural networks as the projecting model, the method is thus named the Neu-SICR algorithm.

The remainder of this paper is arranged as follows. Section 2 offers an overview of the Neu-SICR algorithm. The problem assumptions and the major innovation in this algorithm are illustrated. Section 3 expands the algorithm verification experiment and its results. Section 4 examines the results and compares the recovery quality of this method with that of conventional methods. Section 5 gives the conclusion of this article and provides an outlook for future research topics on this method.

2. Methodology

In this section, the detailed design of the novel Neu-SICR algorithm is proposed. The first subsection gives the assumptions to the basic environment where this algorithm applies; the second subsection illustrates the algorithm workflow and the necessity of our innovation to SICR; and the third elaborates the innovative part of the Neu-SICR algorithm.

2.1. Problem Assumption

While soil moisture is of great importance in various applications and regional soil moisture recovery is a good contribution to multifarious scenarios, our Neu-SICR algorithm is developed under certain circumstances, such that the functionality and accuracy of this algorithm can be guaranteed.

Assumption 1.

The remotely sensed regional surface soil moisture should be a raster format image in the context of the whole algorithm. In this raster image of remotely sensed surface soil moisture by spaceborne optical sensors, each pixel carries a percentage value as a comprehensive description of the volumetric water content throughout the local soil covered by this pixel and close to the ground surface. This percentage should be acquired by a certain inversion algorithm from original remote sensing data, such as a multispectral ground reflectance image, a microwave ground reflectance image, an image of water or vegetation-related indices. Such a regional surface soil moisture image is called a “moisture image” as an abbreviation in the following context. Moreover, the moisture image to be recovered is hereafter called the “target image”, and the moment when the target image is represented is hereafter called the “target moment”.

Assumption 2.

The Neu-SICR algorithm is intended to recover the moisture image where the historical moisture image records a past period and a number of in situ soil moisture observatories that spread over the region quasi-uniformly, and the local surface soil moisture is recorded simultaneously with the remotely sensed data that are available.

Assumption 3.

The Neu-SICR algorithm can recover moisture images only where land use conditions remain unchanged, not only throughout the whole past period from when historical data are utilized (namely, the “historical period” as an abbreviation) but also until the target moment.

Assumption 4.

Although the Neu-SICR algorithm processes the moisture image at the pixel level with a high spatial resolution, a pixel of the moisture image covers an area where meteorological and geographical conditions are heterogeneous. This heterogeneity makes the remotely sensed soil moisture on each pixel a synthesis of various soil moisture conditions throughout the whole area.

2.2. The Innovation of the Neu-SICR Method Compared with the Original SICR Method

The novel Neu-SICR method proposed in this paper has basically inherited the algorithmic structure of the original SICR method that was proposed in a previous paper [44]. Similar to the original SICR algorithm, the Neu-SICR algorithm also recovered a soil moisture image in a 4-stage manner. Because the Neu-SICR algorithm has modified only the first stage recovery process, we provide a detailed description of only this stage. For completeness, Figure 1 illustrates the whole workflow of both the SICR and Neu-SICR algorithms and the differences between them.

The first stage of recovery processes a category of moisture image pixels, namely, the C1 pixels, for which in situ soil moisture observations are available. The soil moisture value in a C1 pixel of a moisture image represents an integrated soil moisture condition in the area covered by this pixel. This area, under the circumstances of spaceborne high resolution optical remote sensing, is regarded as a square ground at the scale of tens to hundreds of meters. At the same time, the soil moisture observatory in this C1 pixel provides continuous and all-weather surface soil moisture observations.

Since a local neighborhood at the image resolution scale usually has uniform weather conditions, these two soil moisture values from the same neighborhood are correlated. In the temporal dimension, this relation would not vary throughout the whole historical period until the target moment because Assumption 3 stated that land use conditions remain unchanged. Therefore, modeling the relationship between a C1 pixel soil moisture and the in situ soil moisture reading from historical records can recover a C1 pixel on the contaminated target image through in situ soil moisture reading at the target moment.

Although the in situ soil moisture observatory is located inside this C1 pixel, its in situ moisture value represents the soil moisture condition in only a fraction of a cubic meter of soil [46], which is much smaller than the high spatial resolution of remote sensing soil moisture images, which are the concern of this paper. Therefore, as previously assumed in assumption 4, environmental heterogeneity within a C1 soil moisture image pixel and this scale difference lead to an inequality between the C1 pixel soil moisture value and the in situ soil moisture value. Although these soil moisture values are correlated, this relation is therefore determined by the local environmental conditions and thus have countless variations.

Nevertheless, because of the advancement of machine learning methods and artificial neural network techniques, novel solutions to modeling intricate relationship have become available. With the help of artificial neural networks, it becomes possible to present arbitrary approximations to arbitrary mappings, including implicit models and relationships, such as projection between in situ soil moisture values and C1 pixel soil moisture [47]. However difficult it is for this relation within this pair of soil moisture observations to be physically modeled, it can be learned by machine learning methods and represented by artificial neural networks from historical observation series.

The novel Neu-SICR recovery algorithm presented in this paper thus takes an artificial neural network, specifically the feedforward neural network (FNN), as a substitution for linear models in the SICR algorithm and models the relationship between C1 pixel soil moisture and in situ soil moisture observations. Basic theory, detailed model construction and training methodology are described in Section 2.3.

2.3. Artificial Neural Networks and C1 Pixel Recovery

2.3.1. The Feedforward Neural Network

A feedforward neural network (FNN) is an artificial neural network that contains an input layer, an output layer, and one or more layers between them. The neurons in each layer are connected toward all neurons in the next layer by weighted edges. Input numerical patterns pass through these connections, carrying different weights, from layer to layer, and sum up at each neuron, and then, the output of the FNN is finally formed.

In our algorithm, for each C1 pixel and the corresponding in situ soil moisture inside, in situ soil moisture values are fed into an FNN input and corresponding C1 remote sensing soil moisture values are acquired from this FNN output. The in situ soil moisture values are thus transformed into values of the C1 pixel where this in situ observatory locates. The structure of the feedforward neural network utilized as the C1 pixel recovery model is shown in Figure 2.

When this FNN is initially set up before being trained, the weights on the edges between the layers and neurons are initialized. The progress to make the initial network a projection from in situ soil moisture values to C1 pixel values needs to adjust the weights on these edges. This process is network training, with the help of true in situ soil moisture and C1 pixel value pairs from the historical record. After sufficient training, the FNN can serve as a good fit of the projection from in situ soil moisture values to C1 pixel values, although this projection is not in an explicit functional form.

2.3.2. C1 Pixel Recovery Algorithm Based on the FNN

As stated above, the advantages of an artificial neural network in modeling implicit relationships drive the innovation of this Neu-SICR method to model projection from in situ soil moisture to C1 pixel soil moisture on a target image. The major steps in recovering each C1 pixel through Neu-SICR are as follows. To recover all C1 pixels on the target image, duplicating these steps on each C1 pixel is required.

Initial Model Building

To recover the C1 pixel value on a target image from in situ soil moisture, an FNN is utilized as the model for projection. This model is hereafter called the “C1 recovery model”. The number of hidden layers and the number of neurons in each hidden layer define the structure of an FNN, and the initial weights on the edges between neurons are randomly initialized. Once these numbers of layers and neurons are given, the FNN is initialized.

Training Data Definition

Once initialized, this C1 recovery model is trained to fit the relationship implied in the historical soil moisture pairs in the next step. As stated in Assumption 2, every C1 pixel can provide a remotely sensed surface soil moisture on this pixel at every moment when historical remote sensing data are available. At the same time, the in situ soil moisture observatory located in this C1 pixel also provides a contemporarily observed surface soil moisture.

These two data sources thus form a pair of historical soil moisture observations with respect to this C1 pixel at one historical moment. With many soil moisture images and contemporary in situ observations available in the archives, such soil moisture pairs at different moments form a time series. These soil moisture pairs later serve to train the C1 recovery model and are thus called “training pairs”.

Model Training and C1 Moisture Recovering

To train an FNN, the in situ soil moisture value of each training pair is input to the neural network. The output of this network is compared with the contemporary C1 soil moisture in this pair, and an error between them is assessed. This error is later utilized to adjust the weights in the neural network, making the network fit this training pair better. In each round of training, all soil moisture pairs of this C1 pixel train the network in this manner one by one. An iterative training procedure can thus take several rounds of training until certain criteria are fulfilled.

Once an FNN is well trained and fulfills these criteria, it fits the relationship from in situ soil moisture to C1 pixel soil moisture within a certain error level, and it can project in situ soil moisture to C1 pixel values. It therefore becomes the C1 recovery model of this C1 pixel. Since training a neural network is not among the major innovations of our Neu-SICR algorithm and many popular neural network training algorithms are available, a detailed description is omitted here. For more details on artificial neural network training, readers are suggested to refer to the literature [48,49,50].

After the C1 recovery model is well trained, the in situ soil moisture at the target moment is input to the C1 recovery model, and the model’s output is the recovered soil moisture at this C1 pixel on the target image. A C1 pixel value of the target image is thus recovered.

C1 Recovery Result Selection

A machine learning model’s training result could be influenced by the initial weights in the neural network. While these weights are randomly initialized in our algorithm, C1 recovery models and consequent recovered C1 pixel soil moisture might be unstable when the training dataset is not sufficiently large. To stabilize the recovery results, a number of model training and C1 pixel recovering trials for each C1 pixel must be conducted in the Neu-SICR algorithm, and on these trials, some result selection criteria are executed.

In the Neu-SICR algorithm, each C1 recovery model’s quality is estimated by two criteria. One criterion is how well they recover the training data, and the other criterion is how close the recovered target soil moisture value is to the contemporary in situ soil moisture value.

To achieve the best C1 recovery model, many repeats of neural network training and verification for each network shape are conducted. In each repeat, a C1 recovery model is trained first, and the C1 pixel series in the training data as well as the target soil moisture value are recovered thereafter. In detail, after training a C1 recovery model, all in situ soil moisture values on this C1 pixel are input to the model one after another, and a series of recovered historical C1 pixel values followed by the recovered target value are output by the C1 recovery model.

For each repeat, the FNN-recovered historical series are compared to its true historical series. Their similarity is measured by a weighted correlation coefficient between the two series. The definition of this weighted correlation coefficient is given in Equations (1)–(3).

$$m(x;w)=\frac{{\displaystyle {\sum }_i{w}_i{x}_i}}{{\displaystyle {\sum }_i{w}_i}}$$

(1)

$$\mathrm{cov}(x,y;w)=\frac{{\displaystyle {\sum }_i{w}_i(x_i-m(x;w))(y_i-m(y;w))}}{{\displaystyle {\sum }_i{w}_i}}$$

(2)

$$corr(x,y;w)=\frac{\mathrm{cov}(x,y;w)}{\sqrt{\mathrm{cov}(x,x;w)\mathrm{cov}(y,y;w)}}$$

(3)

The weighted correlation coefficient between the recovered historical sequence and the true historical sequence basically follows the conventional correlation coefficient. Firstly, the weighted mean of all variables in each sequence is computed with Equation (1). In this equation, vector $x$ is either the FNN-recovered historical series or the true historical series for comparison. All elements in these series are indexed throughout by variable $i$. Thereafter, the weighted covariance between these two sequences is achieved using Equation (2). In this equation, vectors $x$ and $y$ are the FNN-recovered and true historical series, respectively. Finally, the weighted correlation coefficient between the recovered and true historical sequence is defined by Equation (3). In Equations (1)–(3), $w$ is the weight vector that adopted the inverse distance weighting mechanism and differentiates the importance of each soil moisture value along a series. Considering the fact that the recovery quality with a soil moisture condition that is closer to the target soil moisture condition is more important in judging the recovery quality, a recovery value at this date is given higher weight. The weighting is defined in Equation (4)

$$w_i=\exp (\frac{-2\times \left|s{m}_i-s{m}_t\right|}{\frac{1}{n}{\displaystyle {\sum }_j\left|s{m}_j-s{m}_t\right|}})$$

(4)

where $s{m}_i$ is the in situ soil moisture value on date i, and $s{m}_t$ is the in situ soil moisture value at the target moment.

For each repeat, the quality of the C1 recovery model is measured by this weighted correlation coefficient, and then, this measure is thresholded. Only those models that have larger than 0.5 weighted correlation coefficients are regarded as model candidates.

Moreover, the recovered target C1 pixel value by each model candidate is compared to the contemporary in situ soil moisture. Among all model candidates, the one who recovers a target soil moisture value closest to the in situ soil moisture value is selected as the best C1 recovery model. For clarity, these criteria are also described in Equation (5).

$$\begin{array}{l}{t}_{\mathrm{s}}=\arg \underset{t}{\min }\left|in\_situ(s,d_{\mathrm{target}})-s{m}_{rec}(s,d_{\mathrm{target}},t)\right|\\ and\\ corr(sm(s,:),s{m}_{rec}(s,:,t_{\mathrm{s}});w)>0.5\end{array}$$

(5)

In this equation, $t_{\mathrm{s}}$ is the selected best trial of a C1 pixel $s$, $in\_situ(s,d_{\mathrm{target}})$ is the in situ soil moisture reading at station in C1 pixel $s$ on date $d_{\mathrm{target}}$. Moreover, $s{m}_{rec}(s,d_{\mathrm{target}},t)$ is the recovered soil moisture value by a trial $t$ at C1 pixel $s$ on date $d_{\mathrm{target}}$. In the second equation, $s{m}_{rec}(s,:)$ is the historical remotely sensed soil moisture series on C1 pixel $s$, and $s{m}_{rec}(s,:,t_s)$ is the recovered historical remote sensing soil moisture series on C1 pixel $s$ by trial $t_{\mathrm{s}}$.

Following these steps on each C1 pixel, the soil moistures on the C1 pixels of the target image are recovered.

In conclusion, the major innovation of our Neu-SICR algorithm is to take a more flexible model, the artificial FNN, as a substitution of the linear model between the C1 pixel and the in situ observations, to reduce the recovery error of C1 pixels.

3. Study Area and Data

The Neu-SICR algorithm proposed in this paper has been verified by experiments to prove its usability and accuracy. In this section, details of these experiments are provided.

3.1. Experiment Scenario

For the sake of significance in comparison with the original SICR algorithm, the experiments were conducted at the same location as the experiments mentioned in [44].

Thus, the soil moisture data recovered belong to the area located around Huntsville of Tennessee, in the central south of the USA. The experiment zone is a rectangular area that has an extent of 108 km in the east–west direction and 94 km in the south-north direction. As mentioned in [44], this area experiences hot humid summers with average high temperatures of 90°F (32.2 °C) and mild winters with an average low temperature of 49°F (9.4 °C). Precipitation in this area is at 1379 mm annually on average. At the same time, 3 reasons cause the experiment area to have research value. First, agricultural land constitutes more than half of this region, where soil moisture is one of the most important factors in agricultural production, and measuring and monitoring regional soil moisture has been endowed with great importance here; second, an ideal number of in situ soil moisture sensors located uniformly in this area provide continuous observation and abundant data for neural network training. Driven by the above reasons, this area is ideal to be chosen for the Neu-SICR algorithm verification.

3.2. Data

3.2.1. Remotely Sensed Data

Remotely sensed data adopted for verifying the Neu-SICR algorithm were satellite imagery. As an economical and efficient data source, the multispectral images produced by 4 WFV (wide field of view) sensors onboard the Chinese GF-1 satellite were utilized. The WFV sensors onboard the GF-1 satellite can conduct frame mode ground imaging in the nadir direction as well as in the off-nadir direction with satellite agility, with a spatial resolution of 16 m. These multispectral sensors provide imagery in 4 bands, and the wavelength ranges of each are listed in

Table 2. Band information of the WFV sensor onboard the GF-1 satellite.

Band Number	Band Name	Wavelength Start (nm)	Wavelength End (nm)
1	Blue	450	520
2	Green	520	590
3	Red	630	690
4	NIR	770	890

. The field of view of these sensors’ mosaic expands to be as wide as 830 km. The WFV sensors can thus recover any place globally in 4 days. The bands’ distribution makes it possible to regress remotely sensed soil moisture, and the field of view guarantees covering the scenario in a single flight all at once, while the revisit period provides the possibility of abundant historical observations. Moreover, the GF-1 WFV dataset utilized in this paper can be accessed from the CCRSDA website [51] free of charge. All these factors made it a good choice to adopt GF-1 WFV imagery for these experiments.

As mentioned above, for comparison with the original SICR algorithm, the same dataset used also in the original SICR algorithm paper was adopted here. Here, 9 of the 12 frames of A1 grade images used by Xiang Zhang and Nengcheng Chen in [44] made up the remotely sensed data set because the other 3 images were largely contaminated by clouds. These images were observed since 10 March 2014 until 17 October 2014 and were numbered in ascending sequence with respect to observation date. The observed date and time of each image are listed in

Table 3. Acquisition date and time of the experimental remote sensing data.

No.	Acquisition Date and Time (Local Time)	No.	Acquisition Date and Time (Local Time)
1	10 March 2014 16:56	6	31 May 2014 17:00
2	31 March 2014 17:09	7	14 September 2014 16:49
3	11 April 2014 16:39	8	22 September 2014 16:45
4	20 April 2014 16:58	9 (target image)	17 October 2014 16:55
5	6 May 2014 16:50

. In our verification experiment, images 1 to 8 served as historical data, and image 9 served as the ground truth image, which was recovered as the target image.

3.2.2. In Situ Soil Moisture Data

The experiments to verify the Neu-SICR algorithm also required in situ observations simultaneous with respect to the remotely sensed imagery. In this experiment, in situ soil moisture values observed by probes at soil moisture observatories among the soil climate analysis network (SCAN) [52] were traced and adopted.

The SCAN is a continental-scale sensor network that was established by the U.S. Department of Agriculture (USDA)-Natural Resources Conservation Service (NRCS)-National Water and Climate Center in 1999 and has been continuously growing to provide in situ soil moisture calibration and validation datasets. In the experiment scenario, 11 soil moisture observatories from the SCAN could be accessed. Each of them contains in situ soil moisture sensors [Hydraprobe Analog (2.5 Volt)] that provide soil moisture values at different depths below the Earth. We chose the uppermost observations, which represent the soil moisture 0.05 m below the ground surface to match the remote sensing dataset because the GF-1 WFV sensor spectra can hardly penetrate the soil. The series numbers, names and location information of these observatories are listed in

Table 4. In situ soil moisture observatories’ information.

Series Number in U.S. Department of Agriculture (USDA)	Observatory Name	Geographical Location	Pixel Coordinate in Image
2053	Wtars	34°54′N; 86°32′W	(2104, 3551)
2054	Hytop	34°52′N; 86°6′W	(2295, 6008)
2055	Hodges	34°27′N; 86°9′W	(5208, 5747)
2056	Stanley Farm	34°26′N; 86°41′W	(5364, 2705)
2057	AAMU-JTG	34°47′N; 86°33′W	(2936, 3440)
2058	Hartselle Usda	34°26′N; 87°0′W	(5367, 867)
2059	Newby Farm	34°51′N; 86°53′W	(2456, 1553)
2075	McAllister Farm	35°4′N; 86°35′W	(996, 3204)
2076	Allen Farms	35°4′N; 86°54′W	(931, 1494)
2077	Eastview Farm	35°8′N; 86°11′W	(428, 5479)
2078	Bragg Farm	34°54′N; 86°36′W	(2175, 3151)

.

4. Experiment and Results

This section describes every detail of the algorithm verification experiment that we conducted. Before applying the Neu-SICR algorithm, data were pre-processed following the steps listed at the end of this article in Appendix A. After pre-processing, the following experiment was conducted.

4.1. C1 Recovery

Following the Neu-SICR algorithm described in Section 2, the algorithm verification experiment started by recovering C1 pixels. In this section, the details and parameter settings of this experiment are introduced.

4.1.1. Network Shape Design

As introduced in Section 2.3, an artificial FNN was built up in recovering each C1 pixel. Due to the limited archive of WFV multispectral images at the experiment area, historical soil moisture series consisted of only 9 images. This led to limited training samples for the C1 pixel recovery model and thus limited the complexity of this network. For this reason, to fully train the neural network and avoid over-fitting to the historical soil moisture pairs, the recovery model for each C1 pixel was designed to be an FNN with one hidden layer.

For the number of neurons on the hidden layer, different trials were made to determine the best model. Experience revealed that 10 neurons on one hidden layer is sufficient to project almost any functions between one-dimensional input and one-dimensional output. Moreover, Zhang and Chen [44] showed that remote sensing soil moisture values of C1 pixels closely follow a linear relationship with in situ soil moisture. Thus, all trials were designed to contain 2–4 neurons on one hidden layer, to provide a variety of projection models as well as to prevent over-fitting.

4.1.2. C1 Pixel Recovery Result

After selecting the best C1 recovery model following Section 2.3.2 on each C1 pixel, the C1 pixel value of the target image is acquired. Figure 3 illustrates the C1 recovery models for each C1 pixel.

From the figures, it is easy to distinguish that remotely sensed soil moisture series at C1 pixels do not always equal the in situ soil moisture; thus, the sample points in these figures do not fit a straight line. The selected C1 recovery models appear as irregular curves in the in situ observations in the remote sensing observation space.

It is necessary to clarify that in the right part of figure (k) there appears a mismatch situation, which could result from a local minimum in the training process. However, because the to-be-recovered soil moisture is located far from the mismatch region (in the center part of figure (k)), this situation does not affect the recovery result. In fact, the weighted correlation coefficient technique in Section 2.3.2 enhances the importance of the training samples close to the target soil moisture; thus, the FNN model always fits the training data well enough around the target soil moisture. Consequently, even if such a local minimum in figure (k) occurs, they result in only a mismatch of the soil moisture conditions far from target soil moisture and will not lead to a large recovery error.

4.2. C2–C4 Recovery

4.2.1. C2 Pixel Selection and Verification Criterion

Following the workflow of the original SICR algorithm [44], after recovering C1 pixels, C2 pixels were selected and recovered.

On the multispectral WFV image acquired on 22 September 2014, the distance of each pixel and spectral distance with respect to its closest C1 pixel neighbor were computed. Since the dataset were adopted from the original experiment conducted in [44], all thresholds and equations were kept as originally introduced by Xiang Zhang and Nengcheng Chen. Finally, 31,863,518 pixels on the whole target image were selected as C2 pixel candidates.

As the original SICR algorithm stated, after selecting the C2 pixel candidates, linear models were applied on each of them with their center C1 pixel. These linear models were fit to the historical soil moisture pairs sequence, in an attempt to express the relationship between C1 pixel soil moisture and C2 pixel soil moisture. Thereafter, a linear model of each C2 pixel candidate recovered the historical soil moisture series on this C2 pixel, and the recovered series was compared with the original historical series. The Pearson product-moment correlation coefficient (called the p value in the original SICR algorithm) and the r value were computed to filter out fake C2 pixels, where linear models did not fit their series well. After this verification, 15,612,346 pixels, which covered 39.21% of the whole target image, were kept as recovered C2 pixels in the target image. The target image with C1 and C2 pixels recovered is shown in Figure 4.

4.2.2. C3 Pixel Verification Criterion

As the original SICR algorithm is designed, after acquiring C2 pixel values, the other gaps on the target image were examined for whether they present a linear trend with respect to time.

A linear model was fit to each gap pixel’s historical series of “time tag-soil moisture” pairs. As above, to recover C3 pixels, the Pearson product-moment correlation coefficient (called the p value in the original SICR algorithm) and the r value were taken as verification criteria to judge whether the pixel’s historical soil moisture series showed a significant enough trend with respect to time, and only those pixels whose fitting result matched the criterion were selected as C3 pixels. In this part, 2,425,911 C3 pixels were recovered, which covered 6.09% of the whole image.

4.2.3. C4 Recovery with ArcMap Software, the Tool Selection and Parameter Details

After the aforementioned experiment steps, 21,778,760 pixels on the target image, which cover 54.70% of the whole image, were left, including the water areas where pixels did not need recovery. For simplicity, we temporarily regarded them all as C4 pixels and would mask out the water area later. These pixels did not have in situ soil moisture observatories inside, nor did they have linear variation when changing with time, or a spectral similarity with a close C1 pixel. Therefore, relying on only the similarity within a neighborhood allows for their soil moisture to be deduced; thus, a geostatistical interpolation method, the ordinary Kriging, was utilized.

To fulfill the C4 pixel recovery by ordinary Kriging, the ArcMap 10.1 software was utilized. In this software, a Geostatistical Wizard tool could provide semi-automatic analysis to the statistical distribution of the recovered C1 to C3 pixel soil moisture. This tool could analyze the C1 to C3 pixels, extract the range, nugget, and other parameters of semivariogram for the soil moisture values on C1 to C3 pixels. Afterward, it built an interpolation to fill the gaps in between.

Specifically, after analyzing the recovered C1 to C3 pixels, the Geostatistical Wizard tool used an exponential model to fit the semivariogram of the C1 to C3 pixels’ soil moisture distribution. The results showed that the range of this semivariogram equaled 12,722.4536 m, the partial sill equaled 6.2460, and the nugget size equaled 28.0120. An interpolation was therefore built up and filled the C4 pixel gaps on the target image.

Afterward, a mask of the water area was applied on this raster image, and water areas in this experiment region were masked out.

4.3. Reconstructed Soil Moisture Result

Following the steps above, the target soil moisture image was recovered, as shown in Figure 5. In the following subsections, the results of the algorithm verification experiment are examined, and the recovery errors of each part are illustrated.

5. Discussion

To illustrate the applicability, quality and efficiency of the proposed Neu-SICR algorithm, a discussion is given. Later, further improvement possibilities in this research are given in this section.

5.1. Accuracy and Precision of Neu-SICR

5.1.1. Error in C1 Recovery

According to the algorithm design, the C2 pixels recovery model projects C2 pixels from recovered C1 pixels, and the C4 pixel recovery source also includes C1 and C2 pixels. At the same time, C1, C2 and C4 pixels cover 93.91% of the whole recovery image; thus, errors of the C1 pixel recovery dominate the major error rate of recovery. We therefore analyze this part first.

In our algorithm verification experiment, as stated above in Section 3, 11 neural networks and the corresponding C1 pixel values were selected following the given criteria.

Table 5. Reconstruction result of C1 pixels.

C1 Pixel No.	True C1 Moisture (vol %)	Recovered Moisture (vol %)	Relative Error (%)	Number of Hidden Layer Neurons
1	33.0332	37.2839	12.8681	4
2	26.4000	28.9836	9.7867	4
3	35.9182	36.8899	2.7055	4
4	33.8506	41.6336	22.9923	4
5	31.4491	30.3410	−3.5234	4
6	32.3133	23.1040	−28.4998	4
7	34.0566	30.4689	−10.5343	4
8	28.7871	33.2374	15.4595	4
9	30.2760	30.6928	1.3768	4
10	35.5161	30.2037	−14.9576	4
11	34.5329	34.8766	0.9955	4

offers a compact conclusion of the recovered 11 C1 pixels. With the 11 C1 pixels recovered as the table shows, the C1 pixels recovering the mean square error equals 21.2265.

5.1.2. Overall Recovery Relative Error Range and Distribution

After recovering the whole target image, the recovery error is acquired compared with the remotely sensed soil moisture image on 17 October 2014 in the dataset, while considering the latter as the ground truth. Among all pixels, the maximal overestimate relative error is 630.18%, the maximal underestimate relative error is −682.38%. Although these two extrema are large, of all pixel relative errors, the first quartile is −18.98%, the median is −8.60%, and the third quartile is −1.86%. These statistics prove the high accuracy of this Neu-SICR algorithm. Figure 6 illustrates the distribution of relative errors within range [−100%, +100%], in which 38,274,628 pixels covering 96.13% of the whole target image are included. The others include 1539058 pixels of water area covering 3.86% of the whole target image and 3342 pixels of outliers covering 0.0084%. On the other hand, 3,034,1086 pixels have relative errors within the range [−20%, +20%], covering 76.20% of the target image.

5.1.3. Overall Recovery Error Range and Distribution

From the above recovery result, the absolute error of the target image recovery is analyzed. Although the extrema of the largest underestimate error reaches −21729.240 vol % and the largest overestimate error reaches 43.338 vol %, the first quartile of errors is −5.9790 vol %, the median is −2.7579 vol %, and the third quartile is −0.6123 vol %. Moreover, only 1070 pixels are error outliers worse than −100 vol % error, which cover only 0.002687% of the whole target image. On the other hand, pixels whose recovery error within the range [−10 vol %, +10 vol %] total 34134985 and cover 85.73% of the target image. A histogram of the recovery errors except for the aforementioned 1070 outliers is shown in Figure 7a.

To compare the Neu-SICR with the original SICR algorithm, the results in the original SICR paper are taken for comparison.

In the original SICR algorithm paper, Xiang Zhang and Nengcheng Chen provided a histogram of the recovery error distribution, as in Figure 7b. This histogram illustrates the error distribution of the recovered target image. In our experiment, such a histogram is also extracted from the difference image between the recovered target image and the reference true observation on 17 October 2014.

5.1.4. Performance Comparison between Neu-SICR and SICR

Although the difference between Figure 7a,b appears to be insignificant, the statistics of the Neu-SICR and SICR algorithm recovery errors listed in

Table 6. Statistics of recovery errors between the Neu-SICR and SICR algorithms.

	Recovery Relative Error (%)				Recovery Error (vol %)
	1st Quartile	Median	3rd Quartile	Inter Quartile Range	1st Quartile	Median	3rd Quartile	Inter Quartile Range
SICR	−34.75	−14.61	−1.89	32.86	−10.59	−4.48	−0.47	10.12
Neu-SICR	−19.64	−8.90	−2.13	17.51	−5.98	−2.76	−0.61	5.37

give a quantitative comparison of these two methods.

On consideration of the recovery accuracy, the median values of the relative error and recovery error (soil moisture difference) by SICR and Neu-SICR are compared. In Table 5, the relative error median value of the Neu-SICR algorithm is closer to zero than that of the SICR algorithm. The same outcome occurs for the median value of the recovery error (soil moisture difference). These facts clarify that the Neu-SICR algorithm has a higher recovery accracy than the SICR algorithm.

On the other hand, considering the recovery precision, quartile values and inter-quartile ranges are compared between the SICR and Neu-SICR algorithms. Table 5 shows that Neu-SICR has smaller inter-quartile ranges for both the relative error and recovery error (soil moisture difference) than the SICR algorithm. This fact clarifies that the recovery error of the Neu-SICR algorithm is more concentrated and therefore that the Neu-SICR algorithm has a higher precision than the SICR.

Moreover, we also utilize two indices, namely, the average relative error (ARE) and the universal image quality index (UIQI), for assessing the recovery quality, as they were used in [44]. For simplicity, their detailed definitions are omitted here. For those details, please refer to [44,53]. The comparison of these indices between Neu-SICR and the original SICR, the conventional in situ sensor based reconstruction method (IR), and the satellite sensor based reconstruction method (SR) proposed in [44] is as listed in

Table 7. Comparison of the quality assessment indices between the Neu-SICR and conventional methods.

	ARE (%)	UIQI
Neu-SICR	13.18	0.3143
SICR	19	0.1466
IR	10	0.0286
SR	22	0.0137

.

In Table 6, the Neu-SICR algorithm is outstanding with its highest UIQI and second highest ARE value. Compared to the original SICR algorithm, our innovation of the C1 recovery model improved both ARE and UIQI. Although the ARE value of Neu-SICR is not as perfect as that of the IR method, the UIQI affirms that Neu-SICR overwhelmingly beats the IR method.

In conclusion, the innovation proposed in this paper has improved the SICR algorithm in terms of the soil moisture image recovery accuracy and precision, and the Neu-SICR algorithm outperforms its predecessor.

5.2. Time Consumption of the Algorithm Verification Experiment

The algorithm verification experiment was conducted on the aforementioned hardware platform, and an acceptable efficiency was achieved. The time consumption of each part of the algorithm is listed in

Table 8. Time consumption for each category of the pixel recovery on the target image using Neu-SICR in comparison with the original SICR algorithm.

Pixel Category	Time Consumption by SICR	Time Consumption by Neu-SICR
C1	2 min (~120 s)	729 s
C2	48 min (~2880 s)	1974 s
C3	20 min (~1200 s)	1408 s
C4	14 min (~840 s)	around 1 h

.

As Table 8 shows, reconstructing such an image of a soil moisture regional distribution takes approximately two hours. Innovation on the reconstruction model and improvement of the reconstruction results did not cause a significant efficiency loss compared to the original SICR algorithm. This efficiency is acceptable for both research and engineering applications. Even in case of flood or drought disaster relief and loss assessment applications, such time consumption also makes Neu-SICR applicable when an urgent reaction is requested.

5.3. Applicability of Neu-SICR

Conclusively speaking, the algorithm verification experiment successfully recovered a soil moisture image of the experiment area corresponding to 17 October 2014. On this image, all pixels except for those for water areas are given soil moisture values similar to the historical soil moisture images. This recovery was accomplished based on historical remotely sensed soil moisture images series and contemporary in situ soil moisture series as well as the in situ soil moisture observations on the target moment.

Since no remote sensing soil moisture information on the target moment is required, the proposed Neu-SICR algorithm is applicable in recovering regional soil moisture information when this region is totally contaminated by bad weather or when remote sensors, especially satellite optical sensors, have no visibility over this region.

5.4. Merits and Limitations

From the aforementioned algorithm verification experiment and quality assessment, the conclusion can be drawn that the Neu-SICR algorithm can recover remote sensing soil moisture images under the total absence of remote sensing images at the moment when regional soil moisture is required, with the available historical remote sensing soil moisture archive in combination with contemporary in situ soil moisture observations. Although this algorithm is a partial innovation based on our previous work, there are still distinguishing features for our conclusion, as follows.

• This algorithm is an upgrade to our previous work, the SICR algorithm. To the best knowledge of the authors, this Neu-SICR algorithm is the first recovery method that utilizes machine learning and artificial neural networks on soil moisture image reconstruction. This algorithm has adopted the major structure of the SICR algorithm and has added an innovation on one of the four reconstruction rules; thus, it has inherited the merits of the SICR algorithm and makes further improvement upon it.
• The Neu-SICR algorithm has utilized machine learning in modelling the relationship between the local soil moistures at different scales. With the increasing accessibility of various types of remote sensing data, abundant archives of remote sensing soil moisture images could be expected. Therefore, machine learning, as a category of the most popular big data analysis tools recently, are among the best choices in analyzing soil moisture spatiotemporal patterns. On the other hand, with a soaring amount of remote sensing data available, data mining becomes a more and more complex topic. Under this circumstance, as a powerful data analysis approach, machine learning becomes the best choice for accomplishing these missions. In this respect, our Neu-SICR algorithm is not only suitable for the present requirements but also essential for future applications.
• In addition, artificial neural networks are capable of projecting arbitrarily complicated function projections. Since this relationship between local soil moistures of different scales is highly related to environmental conditions, it is thus too complicated to be represented by physical models or explicit functions; as a result, an artificial neural network therefore becomes the best choice to model this relationship and reconstruct soil moisture images. Taking an artificial neural network as the model in Neu-SICR is therefore the best choice for fusing in situ and remote sensing soil moisture observations. Although this model has been used in soil moisture inversion algorithms [54,55], this study is to the best of our knowledge the first to use this approach in soil moisture image reconstruction.
• In addition, as an upgrade to the original SICR algorithm, the Neu-SICR algorithm has the same applicability the SICR but has greater accuracy and better precision, as proven by our experiments. Quantitatively speaking, the overall reconstruction average relative error is improved from 19% by SICR to 13.18% by Neu-SICR; the UIQI between the reconstructed image and the true moisture image is more than doubled, from 0.1466 by SICR to 0.3143 by Neu-SICR. Since the majority of pixels are reconstructed based on C1 pixels and our innovation is aimed at improving the reconstruction quality of the C1 pixels, these advancements can safely be ascribed to the innovation on the C1 pixel recovery model. At the same time, when considering the algorithm efficiency, the Neu-SICR algorithm consumes a similar amount of time than the SICR on a similar platform. We can therefore conclude that Neu-SICR is similarly efficient to SICR.

However, there are still some limitations that lie in Neu-SICR. Since Neu-SICR extracts data relationships that rely on the accessibility and quality of remote sensing and in situ soil moisture observations, the following two issues regarding data sources are crucial.

• First, machine learning models are trained with a large number of samples, and the more training samples that are available, the better the model fits the data. This fact draws a requirement on the abundance of historical remote sensing soil moisture images and contemporary in situ soil moisture observations. If the remote sensing soil moisture archive is not abundant enough, then the relation between remote sensing and in situ soil moisture values cannot be fully represented by historical observation pairs, and in this case, this relation cannot be well extracted by machine learning models.
• Second, the Neu-SICR algorithm reconstructs soil moisture pixels while relying on the local similarity between close regions. If in situ soil moisture observatories are too sparsely located in the region of interest, then soil moisture conditions between too distant regions are badly relevant or could be little related to the models. In those cases, distant pixels to the in situ soil moisture observatories could have low recovery accuracy.
• Moreover, in our experiment, in situ soil moisture observation series encounter gaps where data are required. In those cases, we executed gap-filling methods to overcome such handicaps. However, such gap-filling methods rely on assumptions about the soil moisture spatial similarity or the co-occurrence of soil moisture conditions. Once these assumptions do not fully match the truth, gap-filling methods introduce errors to in situ soil moisture series and therefore introduce errors to reconstruction results. Consequently, better historical series quality avoids such errors.

6. Conclusions

In this paper, we proposed a novel improvement on the SICR algorithm for recovering remote sensing soil moisture images, with the help of in situ soil moisture observations. The Neu-SICR algorithm structure has been adopted from the SICR algorithm, and the foremost recovery model has been improved with artificial neural networks. The algorithm has been verified, the results have been examined, and comparisons to the original SICR algorithm have proven better reconstruction quality and similar temporal efficiency achieved by the Neu-SICR algorithm.

While conventional reconstruction algorithms rely on partial accessibility of remote sensing data, the Neu-SICR provides the possibilities for harsher situations where full remote sensing images at the target moment are beyond access, and it fuses spaceborne optical remote sensing data with ground based in situ soil moisture observations, realizing regional soil moisture reconstruction in a multi-source data fusion manner. Moreover, the Neu-SICR algorithm, as an upgrade of SICR, utilizes machine learning mechanisms to project in situ soil moisture observations at the meter level scale toward remote sensing soil moisture at the tens of meters’ scale. This manner benefits from extraordinary flexibility of artificial neural network in representing complex correlations between soil moisture at different scales and thus results in higher reconstruction quality than the SICR algorithm.

Further improvements could still be made to the recovery process, including the following: (1) By selecting other optical remote sensing data sources for model training, more abundant training pairs and consequently a better C1 recovery model can be expected; (2) By selecting other remote sensing techniques, such as microwave remote sensing soil moisture data, higher remote sensing soil moisture data quality could contribute to higher recovery quality; (3) By selecting other models projecting C1 pixel values to C2 pixel values and by choosing periodic functions that represent seasonal variation of C3 values, such as the dynamic harmonic regression model, higher recovery quality of C2 and C3 pixels could be expected when historical records are adequate to train these models.