1. Introduction
Precision agriculture is being increasingly considered as an optimal technological approach to improve the efficiency and the productivity of farming and cropping systems [
1]. Monitoring crop growth using remotely sensed biophysical variables such as leaf area index (LAI) or canopy cover (CC) has proven to be very effective for inferring information on crop biomass and yield, useful for field management [
2,
3,
4]. Yield estimation and forecasting at the field scale would allow farm managers to plan their agronomic operations, e.g., sowing, tillage or fertilization, on the basis of expected yield potential. At the district level scale, yield estimation and forecasting is useful to public and private organization, for commercial or planning purposes.
The use of remote sensing (RS) in order to monitor crop growth has considerably increased recently, with the development of new technologies such as hyperspectral sensors [
5] and easier availability of imagery, allowing exploitation of these data in a progressively more effective way [
6]. Particularly, satellite RS is increasingly used in monitoring crops and variables that describe their growth, as it allows the monitoring both of large zones on a regional or district scale [
7], and of smaller areas on a field scale [
6]. The use of these data has proven to be effective in the estimation of crop yield [
2,
8,
9,
10], by combining the monitoring from remote sensing of crop biophysical variables with crop growth models. Leaf area index (LAI), fractional canopy cover (CC), the fraction of photosynthetically active radiation absorbed by the canopy (fAPAR) and plant chlorophyll concentration are the most important canopy variables used in this context, being the main state variables used in crop growth modelling [
11]. A detailed review of the methods for retrieving canopy variables from remote sensing [
11] divided these methods into: (1) statistical approaches, e.g., using vegetation indices and regression methods linking spectral information and biochemical variables [
12]; and (2) approaches exploiting physically-based models [
13,
14,
15]. The latter are particularly interesting, because they are expected to be of more general validity, without the need for data-specific calibrations as in the former methods. Additionally, they often allow to estimate simultaneously several variables such as LAI and CC [
14]. A widely used strategy is to train artificial neural networks (ANNs) using the simulations from a canopy radiative transfer model such as PROSAIL [
16], which couples the leaf model PROSPECT [
17] and the canopy model SAIL [
18]. Many studies have shown the effectiveness of this methodology, using both multispectral [
14,
19] and hyperspectral [
20] sensors.
In order to estimate crop yield, the biophysical variables can be assimilated into crop growth models using different approaches. Following [
21], it is possible to distinguish two strategies: calibration and updating. The calibration approach consists of re-calibrating the model parameters in order to minimize the differences between simulated and observed variables. In the updating approach, it is the value of the biophysical variables simulated by the model that is updated, on the basis of the value of the biophysical variables observed e.g., from remote sensing.
Some authors have converted the state variables simulated by the models into vegetation indices (VIs) by means of canopy reflectance models and used VIs, derived from RS data, in the assimilation. For example, authors of [
22] developed a methodology in which the LAI simulated by the EPIC crop model was converted into reflectance in the RED and NIR spectral range of Landsat TM or AVHRR data using the SAIL model. NDVI values from these reflectances were then compared with NDVI derived from satellite imagery. The EPIC crop model parameters were re-calibrated for NDVI to be within 20 percent of the observed satellite data [
22]. Other authors have estimated biophysical variables from RS and used them directly in the assimilation. For example, authors of [
23] recalibrated the parameters of the SUCROS model by minimizing the difference between LAI estimated from SPOT satellite data and LAI simulated by the model. The updating approach has also been applied in many studies [
24,
25,
26,
27,
28], in which the effectiveness of this method to improve the accuracy of the crop growth model predictions has always been proven. Authors of [
24] tested the ensemble Kalman filter (EnKF), an updating assimilation method, to assimilate the LAI derived from MODIS into the WOFOST crop model [
29], in order to determine the production of wheat at a regional scale. Authors of [
25] explored the potential of EnKF for simultaneously assimilating two remotely sensed variables, i.e., soil moisture and LAI, demonstrating the possibility of preventing yield losses by monitoring the effects of water stress on crops. The potential of the EnKF method assimilation was also compared with the POD4DVAR, a four-dimensional variational algorithm [
27], assimilating LAI estimated by the CCD sensors on board of the Chinese Huan Jing (HJ) satellites HJ1A/B into the CERES crop model, both at a regional and field scale. The POD4DVAR showed a higher computational efficiency, but was more influenced by measurements uncertainties than EnKF.
Regardless of the approach, in all the studies in which remote sensing data are assimilated into crop models, not all the parameters are recalibrated, because of their large number and the limited information about them available in situ. This implies that the choices on which parameters to recalibrate at run-time and of the values to assign to fixed parameters are crucial [
23]. A study conducted by authors of [
28] highlighted these problems. The green area index (GAI) estimated from MODIS was assimilated in the WOFOST [
29] model using a calibration approach, minimizing the error between modelled GAI and MODIS-observed GAI. Only the parameters that most affect GAI were optimized, highlighting the need to calculate the parameters sensitivity for each scenario [
28].
The efficiency of the assimilation methods is also strongly dependent on the number of observations ingested into the process [
11]. Many studies in the literature (e.g., [
24,
25,
26]) showed that using a higher number of observations corresponds an improved accuracy of estimation [
2]. Generally, the number of observations assimilated into the models is higher than six. In a context of regional scale, there are many satellites which can provide data frequently, albeit at a low resolution (e.g., MODIS). However, for precision agriculture applications, it is necessary to work at the field scale, with a spatial resolution of at least 30 m or higher. The opportunities to obtain a high number of data acquisitions with such resolution are currently rather limited, therefore, in order to apply these methods at the field scale, it is necessary to use efficient assimilation algorithms, performing well even with a limited number of images, or to extend the number of observations in other ways. For example, [
4] tried to solve this problem by using a data fusion algorithm blending MODIS (250 m) and OLI data (30 m) to estimate LAI at the field scale and assimilated the data into the simple algorithm for yield (SAFY) model. The fused data set had the temporal resolution of MODIS data (8 days) and the spatial resolution of OLI (30 m).
In addition to the number of observations, the choice of the crop model to use is also an important factor conditioning the assimilation results. Generally, models that accurately describe the crop growth process have a higher accuracy, but they are more complex, more difficult to integrate with other processes (such as the assimilation methods) and have higher computational costs. In particular, the large number of parameters makes the calibration of the model rather laborious, and this is one of the main problems of the application of assimilation methods. The choice of the model to use, in agreement with the purpose to be achieved, should consider other attributes in addition to model accuracy, such as complexity and plasticity [
30,
31].
Among all the crop models that have been used in assimilation studies, Aquacrop [
32], seems particularly interesting for its relative simplicity, as compared to more complex models, due to its emphasis on water limitation and the explicit use, as main canopy state variable, of CC. This variable is usually easier to estimate from remote sensing than LAI, not being subject to saturation at high values [
31]. The first applications of Aquacrop within data assimilation schemes have provided encouraging results [
31,
33,
34,
35]. However, in Aquacrop there are about 100 parameters related to the characteristics of the crop and the soil, as well as other management and input factors. During the assimilation, authors of [
33] recalibrated 3 parameters, authors of [
34,
35] 8 parameters and authors of [
31] 13 parameters, leaving all the others fixed. Additionally, in the version currently made available by the developers, it is impossible to implement a re-initialization at the RS observation dates, preventing the application of updating approaches of data assimilation, so that only recalibration approaches have been employed so far.
SAFY [
36], a much simpler model than Aquacrop, with fewer parameters, i.e., 13 in the original version, has been also successfully employed for the estimation of wheat yield, using only recalibration assimilation approaches so far [
4,
36]. This model is potentially suitable also for the application of updating assimilation algorithms, given the accessibility of the source code, and it is particularly appealing in this context given its high computational speed [
31].
The aim of this work was to develop and compare two methods for the estimation of winter wheat yield, suitable both at field and district level, based on data assimilation algorithms combining remotely sensing crop biophysical variables with the Aquacrop and SAFY crop growth models.
Because of the above mentioned coding constraints, it was necessary to use different assimilation techniques for the two models, i.e., the EnKF was employed for SAFY, while for Aquacrop particle swarm optimization (PSO) [
37] was used. A dataset, composed by a series of images acquired with multispectral satellite sensors, was used to estimate the LAI and the CC using a model-based method employing an artificial neural network [
14]. Additionally, the purpose of this study was to test the performance of assimilation methods with a reduced number of observations, in order to verify their potential for precision agriculture applications in case of constraints e.g., due to a limited number of satellite acquisitions available within the crop growth season, a situation often occurring in areas affected by frequent cloud cover.
4. Discussion
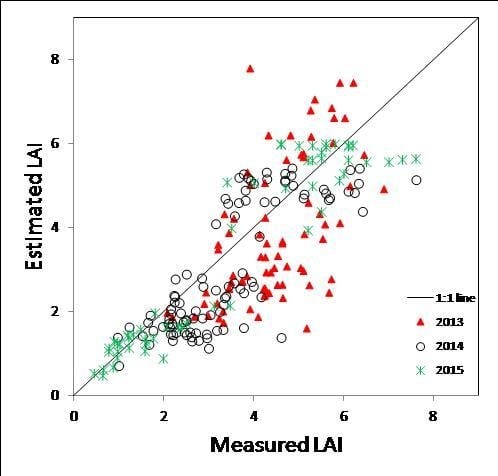
The first step of this work was the retrieval, from remote sensing data, of the biophysical variables to be used in the assimilation procedures. The biophysical variables considered were LAI and CC, both estimated using the ANN algorithm as described in
Section 2.2.2. The results shown in
Figure 4 indicate that overall, the algorithm tended to underestimate the value of LAI. The comparison between estimated values and ground measurements highlighted that, with the exception of small values (between 0 and 2), the points underestimated were more than those overestimated, particularly for values of LAI between 2 and 4, range in which the error was higher than the average RRMSE. This error distribution was partly due to the characteristics of ANN algorithm, which tended to worsen the estimation of winter wheat LAI with increasing values, because of the well-known issue of saturation of the canopy reflectance [
19]. Using HJ-1 data, authors of [
55] obtained better results than ours, for a larger ground dataset collected in the same area of Yangling in 2014 (
n = 80), with RRMSE values as low as 21% for optical vegetation indices. However, it should be noted that the methods used by these authors are based on empirical calibrations, with a prevailing local validity, whereas, in our case, the ANN method is of general application, not requiring preliminary calibrations [
19,
20]. Authors of [
56] assessed the performance of the same ANN-based algorithm used in the present study, with SPOT4 HRVIR and Landsat 8 data, obtaining an RMSE of 0.74 for winter wheat, better than the RMSE values found in our study (
Table 6) for 2013 and 2014, respectively of 1.48 and 1.03, but similar to the that obtained in 2015, i.e., 0.75. It should be noted that in the dataset used by the authors of [
56], only two data points had LAI values higher than 3 and the maximum LAI was 4.5. Conversely, in our dataset, many points had LAI values well above 3, reaching up to a maximum value of almost 8 (
Figure 4).
A considerable impact on the LAI estimation accuracy might have been brought about also by the quality of the remote sensing data. The region of interest is strongly characterized by the presence of clouds and haze, so the probability to acquire clear images is very low, especially during spring, when rainfalls are frequent. The atmospheric correction for these images was difficult and it strongly influenced the reflectance and consequently the estimation of LAI. With such restrictive atmospheric conditions, it is not surprising that radar data can provide better estimates of LAI than optical data [
55]. Indeed, authors of [
55], using empirical calibrations, achieved better results when they included regressors in the estimation of LAI, radar polarimetric parameters obtained from RADARSAT-2, alone or coupled with vegetation indices from HJ-1. In the latter case they achieved a RRMSE of 17.4% when using partial least squares regression.
The consideration about the influence of the atmosphere on the quality of input data for the Yanling area is also true for CC, but in this case the RRMSE between RS estimation and ground measurements was smaller than for LAI, with a RMSE of 7.2% and a RRMSE of 9% for the three years. This is due to the fact that CC is less subject to a saturation at high values than LAI. The observation period was between March and May, when the variation of LAI was between 0.5 and 7, corresponding to a variation of CC between 40% and 91%. By the end of March, LAI was higher than 3, which corresponded to a CC of 80%, so for most measurements dates CC varied between 80% and 91%. In such a small range of values, the ANN algorithm could estimate CC changes with a higher accuracy. In this case our results were better than those achieved by [
56], who obtained a RMSE of 19% for winter wheat, whereas in our study RMSE values ranged between 5.1% and 7.3% in the three years. Our results are also better than those of [
33], who achieved a RMSE of 15.8% and an RRMSE of 19.6% when using only HJ-1 data. These authors obtained better results, comparable to ours, when they used, in empirical regression models, coupled optical and radar data as regressors, reaching a RMSE of 8.8% and a RRMSE of 10.9%, confirming the above considerations on atmospheric effects. Again, it should be remembered that we used a general purpose model-based algorithm, i.e., not requiring a local calibration, unlike [
33]. Part of the differences in the accuracy of estimation of CC could also be attributed to the equations used to convert ground measurement of LAI into CC. We used an equation proposed in [
40] after a specific study on wheat, which showed that it performed better than the equation proposed by [
57] for maize, which was also employed in [
33].
The estimation of LAI and CC was aimed at the application of assimilation methods for estimating yield, thus the error in their estimate could influence the results of the assimilation. In particular, the EnKF method takes explicitly into account the error in the observations to be assimilated into the model, which was set in our case to a value of 30%, in agreement with the RRMSE actually obtained for LAI (
Figure 4). This sort of error is expected to have a remarkable effect on the accuracy of the assimilation results [
2].
SAFY and Aquacrop are two growth crop models with rather different characteristics. The former is a simple algorithm, developed specifically for remote sensing applications, with a reduced number of influential parameters and strongly dependent on the scenario characteristics [
49]. The latter is more complex than SAFY; the number of influential parameters is higher and the influence of scenario characteristics is lower than for SAFY. The strength of Aquacrop is its capability of taking into account crop physiological processes related to water stress, which are ignored by SAFY, but of great interest for the estimation of crop water requirements and yield response to drought from remote sensing [
7,
31]. However, despite being less complex than other crop models such as e.g., EPIC [
22] or CERES [
26], the larger number of parameters of Aquacrop makes it harder to calibrate and slower to run than SAFY, therefore making it less suitable for an assimilation application.
The application of two different assimilation algorithms to the two models, EnKF on SAFY and PSO on Aquacrop, allowed to obtain reasonable yield estimates both at the field and at the district scale. In the field application, the accuracy of SAFY with the application of EnKF was similar or higher than for Aquacrop with PSO. The estimated yields obtained with EnKF and SAFY varied in a range between 3 and 8 t∙ha−1, while for PSO with Aquacrop they varied between 4 and 7 t∙ha−1. The first method estimated with a good approximation low yield values, but the estimation accuracy decreased with the increasing yield and above 6 t∙ha−1 an underestimation was apparent. Instead, the second method overestimated values of yield lower than 4 t∙ha−1 and underestimated values over 6 t·ha−1. Both methods showed the tendency to saturate at values higher than 6.5 t∙ha−1.
Both methods were initially applied by using a single preliminary calibration for the entire dataset, i.e., the three different winter wheat growth cycles. However, in such case, the yields estimated from the PSO with Aquacrop had a rather small range of variation (
Figure 6b), looking rather insensitive to scenario changes. A different calibration for each climate dataset was necessary (
Figure 6c), in order to have comparable results with those obtained applying the EnKF to SAFY, the latter being calibrated only once for all the years. In [
34], PSO method for the assimilation of crop biomass was used, estimated from field based spectral reflectance measurements, into the Aquacrop model, and employed a quite extensive winter wheat dataset collected over 4 years. During the PSO assimilation the authors recalibrated only three parameters (canopy growth coefficient, maximum canopy cover and maximum effective rooting depth), but no information is provided on how the other parameters were set. They achieved an RMSE of 0.65 t·ha
−1 for the whole validation dataset.
Jin et al. [
35] used the same field dataset and methodology as in [
34], but during the PSO assimilation they recalibrated eight Aquacrop parameters: increase of canopy cover per growing degree day (cgc), maximum canopy cover (ccx), decrease of canopy cover per growing degree day (cdc), growing degree days from sowing to emergence (eme), number of plants ha
−1 (num), soil water depletion factor for canopy senescence (psen), shape factor for water stress limiting stomatal conductance (pstoshp), and maximum effective rooting depth (rootdep). Also, in this case no information was provided on the other parameters and input variables. They achieved RMSE values for yield estimates ranging from 0.51 to 0.61 t·ha
−1 for the different years and RRMSE from 8.8 to 10.7%, i.e., much better than our RRMSE value of 24%. However these results were obtained using ground-based hyperspectral measurements. The authors of [
33] used HJ-1 data, acquired in 2014 in Yangling, for estimation of biomass or canopy cover, which was then used for the assimilation into the Aquacrop model using the PSO method. In this case, the yield estimation accuracy was lower, with an RMSE of 1.24 t·ha
−1 and a RRMSE of 26%, comparable with our results. Since, for these authors, the estimation of biomass was more accurate than that of CC; because of the above mentioned issues, they obtained better results when they used biomass for the assimilation, with a RMSE of 0.92 t·ha
−1 and a RRMSE of 19.4%. Even better results were achieved by [
33] when they combined optical and radar data for the estimation of the biophysical variables to be used for the assimilation, reaching a RMSE of 0.81 t·ha
−1 and a RRMSE of 17%. This confirms that the use of radar data could partially overcome the above mentioned difficulties with the atmospheric effects on optical data for the Yangling area.
In the regional scale application, both methods simulated the mean and total yield of the Yangling administrative area with a good approximation, as compared to official statistics. The wheat classification procedure was quite successful and it showed the spatial distribution of growing areas, interestingly revealing the effect of year-to-year variation due to crop rotation practices. Yield estimation results were generally consistent with those obtained with the field scale application. For PSO with Aquacrop the accuracy in the spatialized application was higher than expected from field scale results. It should be noted that for this method it was necessary to recalibrate the fixed parameters and the ranges of parameters optimized during the assimilation, for each observed crop growth cycle. For EnKF with SAFY, conversely, the same calibration was used for all the analyzed crop growth cycles. Because of the computational limits of Aquacrop, the classes in which the pixels were binned were reduced from about 1800 used in EnKF-SAFY to 100 for PSO-Aquacrop. This reduction was one of the causes of the lower spatial variation of yield for Aquacrop (
Figure 8) as compared to SAFY (
Figure 7). Another cause was the low variation of CC, and the input data for PSO-Aquacrop, which affected the output.
Despite the error in the input data, found for both LAI and CC, and the limited number of remote sensing observation dates, the estimation of yield was reasonable. For EnKF with SAFY this depended on the characteristics of the Kalman Filter. This method, in fact, “filtered” the error on the measurements, introduced as a random effect, reducing its influence on the output. The effect of the error can be also reduced by increasing the number of ensemble, but this inevitably increases the computational time. For this method the choice of measurements error variance and the number of ensembles is fundamental [
51].
For PSO with Aquacrop, the input error of CC was lower than for SAFY, but the yield estimation accuracy seemed to be more affected by the calibration of the model for each climatic scenario. This method thus resulted to be strongly dependant on the initial calibration, which resulted rather complex because of the high number of parameters which described the model. This dependence from calibration combined with the inaccessibility of the Aquacrop code and with the high computational cost, made the PSO method with Aquacrop less suitable for an operational application as an assimilation algorithm.
The value of RRMSE obtained with the assimilation based on the EnKF with SAFY ranged, in the present study, between 15% and 20% among the years, with a value of 18% for the whole dataset.
Veloso [
48], using a modified SAFY version including CO
2 fluxes, and recalibrating seven parameters assimilating LAI retrieved from remote sensing, obtained RRMSE values between 12% and 24% for wheat yield estimation. It should be noted that a much larger number of observations of LAI from remote sensing acquisitions were available in [
48] as compared to the present study.
In the literature [
22,
23,
24,
25,
26,
27,
28] the RRMSE value found by applying different methods of assimilation in different models was reported to be between 5% and 16%, therefore quite lower than ours. However, it is important to consider that some of these studies [
24,
25,
27] employed more than 20 observations of biophysical variables in the assimilations for each crop growth cycle, while other studies [
4,
26] used less images (around 10) at a higher resolution and with a lower error on the biophysical variables estimations. The method tested in this study, instead, assimilated a reduced number of images (just three or four) for each crop growth cycle and with an estimation error of about 20%, reaching levels of accuracy in the estimation of the yield comparable with the studies encountered in the literature. Casa et al. [
2] showed that the frequency of available observations, but also their distribution along the crop growth cycle has an important influence on the accuracy of model estimation, when used for model forcing.
5. Conclusions
This study demonstrated the possibility to estimate the winter wheat yield, at field and district level scale, through the use of assimilation methods. Two different approaches were tested, one based on an updating assimilation method, the EnKF, employed for the assimilation of LAI into SAFY, and another based on a calibration assimilation method, the PSO, used to assimilate the CC into Aquacrop. The tests at the field scale showed the feasibility of using medium resolution (30 m GSD) satellite data, such as from HJ1A/B or Landsat 8 OLI images, to estimate yield, with potential applications for precision agriculture.
However, the results obtained with Aquacrop were less accurate as compared to other methods of assimilation for calibration encountered in the literature [
22,
23,
28]. This is mainly due to the characteristics of Aquacrop, for which is indispensable to carry out a very accurate calibration. Nevertheless, the application at the district scale of PSO assimilation with Aquacrop, was in agreement with the yield provided by official statistics. This occurred because Aquacrop was recalibrated for each climate dataset. Furthermore, to meet the high computational requirements of this assimilation method for calibration, a coarser binning of pixels, according to the CC temporal series, was applied, forcing a reduced number of classes. In this way the range of variation of simulated yields was rather limited, leading to accurate results but responding less to spatial or temporal variation of yields. The high computational cost, the difficult calibration and the need to recalibrate for each year of climate datasets makes, therefore, the PSO method applied to Aquacrop less efficient.
The performance of the EnKF with the SAFY model, was comparable with the results of others upgrading assimilation method encountered in literature [
24,
25,
26,
27,
28], which is especially encouraging when considering that, despite the limited number of remote sensing images, i.e., three or four, with an error of LAI estimation of 30%, the error on the yield estimation was around 18%. This allows the application of this upgraded assimilation method in areas of the world where it is not possible to obtain a large number of images for each crop cycle.
The encouraging results of the present work obtained with SAFY should be confirmed with further studies with other validations, possibly with experiments that provide more frequent field measurements, a larger variety of climatic and environmental datasets and a higher quality of remote sensing image collection.