Next Article in Journal
Four-Component Model-Based Decomposition for Ship Targets Using PolSAR Data
Next Article in Special Issue
Modeling the Spatiotemporal Dynamics of Gross Domestic Product in China Using Extended Temporal Coverage Nighttime Light Data
Previous Article in Journal
The 2013 FLEX—US Airborne Campaign at the Parker Tract Loblolly Pine Plantation in North Carolina, USA
Previous Article in Special Issue
Characterizing the Growth Patterns of 45 Major Metropolitans in Mainland China Using DMSP/OLS Data
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 9
Issue 6
10.3390/rs9060620
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Evaluating the Use of DMSP/OLS Nighttime Light Imagery in Predicting PM2.5 Concentrations in the Northeastern United States

by
Xueke Li
1,
Chuanrong Zhang
1,*,
Weidong Li
1 and
Kai Liu
2
1
Department of Geography, University of Connecticut, Storrs, CT 06269, USA
2
Key Laboratory of Water Cycle & Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources, Chinese Academy of Sciences, Beijing 100101, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2017, 9(6), 620; https://doi.org/10.3390/rs9060620
Submission received: 3 May 2017 / Revised: 1 June 2017 / Accepted: 13 June 2017 / Published: 16 June 2017
(This article belongs to the Special Issue Recent Advances in Remote Sensing with Nighttime Lights)
Browse Figures
Versions Notes

Abstract

:
Degraded air quality by PM2.5 can cause various health problems. Satellite observations provide abundant data for monitoring PM2.5 pollution. While satellite-derived products, such as aerosol optical depth (AOD) and normalized difference vegetation index (NDVI), have been widely used in estimating PM2.5 concentration, little research was focused on the use of remotely sensed nighttime light (NTL) imagery. This study evaluated the merits of using NTL satellite images in predicting ground-level PM2.5 at a regional scale. Geographically weighted regression (GWR) was employed to estimate the PM2.5 concentration and analyze its relationships with AOD, meteorological variables, and NTL data across the New England region. Observed data in 2013 were used to test the constructed GWR models for PM2.5 prediction. The Vegetation Adjusted NTL Urban Index (VANUI), which incorporates Moderate Resolution Imaging Spectroradiometer (MODIS) NDVI into NTL to overcome the defects of NTL data, was used as a predictor variable for final PM2.5 prediction. Results showed that Defense Meteorological Satellite Program/Operational Linescan System (DMSP/OLS) NTL imagery could be an important dataset for more accurately estimating PM2.5 exposure, especially in urbanized and densely populated areas. VANUI data could obviously improve the performance of GWR for the warm season (GWR model with VANUI performed 17% better than GWR model without NDVI and NTL data and 7.26% better than GWR model without NTL data in terms of RMSE), while its improvements were less obvious for the cold season (GWR model with VANUI performed 3.6% better than the GWR model without NDVI and NTL data and 1.83% better than the GWR model without NTL data in terms of RMSE). Moreover, the spatial distribution of the estimated PM2.5 levels clearly revealed patterns consistent with those densely populated areas and high traffic areas, implying a close and positive correlation between VANUI and PM2.5 concentration. In general, the DMSP/OLS NTL satellite imagery is promising for providing additional information for PM2.5 monitoring and prediction.

Graphical Abstract

1. Introduction

Fine particulate matter (known as PM2.5, with an aerodynamic diameter less than 2.5 µm) is hazardous to human health [1,2]. Evidence from both long-term and short-term studies of PM2.5 suggests that high levels of PM2.5 can cause high rates of mortality [3,4], contribute to high risks of cardiovascular diseases [5,6], and lead to increased possibility of lung function decline [7,8]. Thus, accurately characterizing the spatiotemporal distribution and variation in PM2.5 concentration is crucial for laying a sound basis for improving public health.
In general, two approaches have been introduced to characterize surface PM2.5 concentration. The first one is to use ground-based PM2.5 monitoring networks. It can provide accurate measurements. However, its spatial coverage is limited and observed data are only available at certain times due to sampling frequencies. In addition, these point measurements are insufficient to explain regional variations, and thus are inevitably subject to errors when estimating PM2.5 concentration at a regional scale [9]. By contrast, remote sensing (RS) technology can provide continuous spatial and temporal observations, which may help to solve the problem faced by monitoring networks. The RS approach uses satellite-retrieved aerosol optical depth (AOD) to estimate PM2.5 pollution in areas where ground-based monitors are too sparsely distributed [10,11,12]. A growing body of work has been done on examining the relationship between RS-retrieved AOD from various sensors and ground-measured PM2.5 [13,14,15,16]. Among them, Moderate Resolution Imaging Spectroradiometer (MODIS) imagery has been demonstrated to be a quality-guaranteed product and has been widely used in predicting PM2.5 concentration [17,18]. Apart from AOD retrievals, meteorological variables and land use information, for instance, have also been utilized to develop more sophisticated statistical models for PM2.5 estimation [14,19,20,21,22,23,24,25]. Results from these studies revealed that the incorporation of meteorological parameters and land use information into the PM2.5-AOD relationship can improve the performance of prediction models.
In the last two decades, the nighttime light (NTL) imagery from the Defense Meteorological Satellite Program/Operational Linescan System (DMSP/OLS) began to play an important role in various studies, including but not limited to detecting human settlements [26], estimating population density [27], and mapping urban extent [28,29,30]. Despite its wide use in demographic and socioeconomic studies, NTL data has received less attention in PM2.5 pollution monitoring, especially in those studies concerning complex regions with both urban and rural settings. Only recently, a couple of studies investigated the effectiveness of DMSP/OLS NTL data in predicting daily PM2.5 average concentration [31,32]. However, the DMSP/OLS NTL data were used as the only input variable in these studies for PM2.5 prediction, and the potential contributions of meteorological variables and AOD measurements were ignored.
This study aimed to evaluate the potential of using DMSP/OLS NTL data, together with satellite-retrieved AOD data and meteorological data, to estimate the ground-level PM2.5 concentration. The study area is the New England region, which is composed of urban, suburban, and rural areas. For this purpose, the geographically weighted regression (GWR) method [33] was chosen for performing PM2.5 prediction. The performance of the specifically constructed GWR models with different input variables was cross-validated, and the spatiotemporal variability of the predicted PM2.5 was demonstrated for the year 2013.

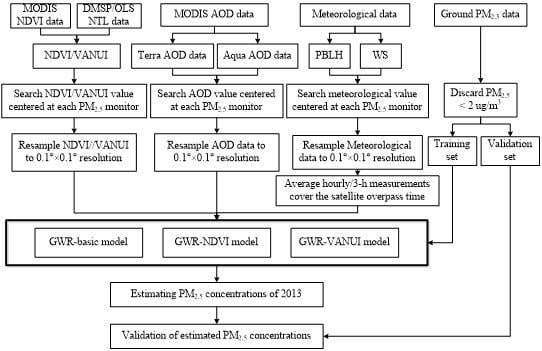
2. Materials and Methods

2.1. Study Area

Our study area is the New England region, Northeastern United States. It comprises the states of Maine (ME), New Hampshire (NH), Vermont (VT), Massachusetts (MA), Connecticut (CT), and Rhode Island (RI) (Figure 1). The entire New England region has an area of approximately 186,460 km2, with a population of 14,444,865 as recorded in 2010. Among the six states, MA is the most populous while VT is the least populous. A prominent characteristic of New England is its densely distributed forests [34], which cover approximately 80% of its total land. Particularly, ME, NH, and VT are among the top four most heavily forested states in the United States. Mean annual temperature ranges from 10 °C in southern CT to 3 °C in the northern highlands of VT, NH, and ME. Mean annual precipitation ranges from 790 to 2550 mm, with more rainfall at higher elevations.

2.2. Data

2.2.1. Ground Measurements

The ground-level PM2.5 measurements over New England from 1 January 2013 to 31 December 2013 were acquired from the US Environmental Protection Agency (EPA)’s Air Quality System [35]. According to Hu, Waller, Al-Hamdan, Crosson, Estes Jr, Estes, Quattrochi, Sarnatand, and Liu [20], PM2.5 values that fall below the detection limit were removed (<2 μg/m3). As a result, 55 monitoring sites were counted for the analysis (Figure 1). Please note that the northern area (mainly ME, NH, and VT, with very low population density and high forest coverage) has fewer PM2.5 monitors than the southern area (mainly CT, eastern MA, and RI, with some large cities and most urban areas).
The meteorological data were derived from two assimilated datasets. The wind speed (WS, m/s) data was obtained from the Phase 2 North America Land Data Assimilation System (NLDAS-2) [36] with a high spatial resolution (1/8th degree, or ~13 km). Since NLDAS-2 does not provide the planetary boundary layer height (PBLH, m) data, our PBLH data was obtained from the North American Regional Reanalysis (NARR) (http://www.emc.ncep.noaa.gov/mmb/rreanl/) dataset, which has a spatial resolution of ~32 km. To be consistent with the satellite overpass time (10:30 a.m. local time for Terra, and 1:30 p.m. local time for Aqua), the mean values of the two variables were calculated for the daily time period from 9 a.m. to 3 p.m. local time.

2.2.2. Satellite Observations

The 2013 MODIS AOD Level 2 product (Collection 5.1) within the study domain was downloaded from a NASA Archive and Distribution System [37]. The AOD data consists of both retrievals from the two satellites, Terra and Aqua. The relatively fine spatial (10 km at nadir) and temporal (1–2 days) resolution of these measurements makes them suitable for characterizing daily PM2.5 concentration at a regional scale. High quality retrievals with Quality Assurance labels 3 were used to avoid introducing potential errors [38].
The annual cloud-free composited NTL data was obtained from a Version 4 F18 sensor (2010–2013) for the year 2013 [39]. This stable light product is the result of discarding visible band values with ephemeral events and replacing background noise with the value of 0. Consequently, the data, recorded as a digital number (DN), ranges from 1 to 63. With a scanning swath of 3000 km, the current stable light product can provide global imagery from 1992 to 2013, with a spatial resolution of 30 arc-seconds (~1 km).
The 2013 MODIS normalized difference vegetation index (NDVI) Level 3 product was acquired from National Aeronautics and Space Administration (NASA)’s Earth Observations (NEO) [40]. Specifically, the Terra satellite observations (MOD13A2), with a spatial resolution of 1 km and a revisit period of 16 days, were used. A detailed description of the MODIS NDVI products can be found elsewhere [41].

2.3. Methods

The predictions of PM2.5 concentration over New England were carried out by incorporating the ground-based PM2.5 measurement dataset and several satellite observation datasets (MODIS, VANUI, and meteorological data) into three specific GWR models with different predictor sets. The results from the proven optimal GWR model were used as the final PM2.5 prediction. The detailed processing steps are illustrated in Figure 2.

2.3.1. Data Pre-Processing and Integration

Before inputting the data of the dependent and independent variables into a GWR model, a uniform data resolution and map projection should be considered. A reprojection was performed to all of the datasets. Then, grid cells with 10 km resolution were built across the New England region. The data of dependent and independent variables were assigned to the nearest grid cells. The distribution of PM2.5 monitoring sites is uneven across the study domain, with more sites clustering in major cities like Boston. For grid cells that contain more than one PM2.5 monitoring site, the mean values of these sites were calculated. Similarly, the averaged AOD values were used for grid cells that contain more than one AOD observation. However, for those grid cells that have only one AOD observation available, an adjustment ratio was applied [42]. The final datasets used in this study are the products derived by spatially matching all the original data to the grid cells.

2.3.2. Model Construction

The relationships between PM2.5 and the predictors vary over space. Such spatial variations have been observed in previous studies [16,43,44,45]. Since the predictors used in our study differ from those previous studies, a comparison between the traditional multiple linear regression (MLR) (using the ordinary least squares estimator) and GWR was first conducted. The comparison showed that GWR outperformed the MLR with an improved mean accuracy of 0.15 in adjusted R2, which means that GWR could explain more variance in PM2.5. Therefore, using global estimation models to describe the relationships will produce less accurate results. The GWR method can estimate the spatial variation and non-stationarity of a continuous spatial variable [33], such as the PM2.5 concentration, at a regional scale. In other words, the regression coefficients in GWR modeling are location-specific instead of being constant globally. More applications of GWR can be found in recent publications [46,47]. In this study, a specific GWR model was designed for PM2.5 prediction. Four main impact factors, AOD, PBLH, WS, and VANUI, were used as explanatory variables to predict PM2.5 concentration in the GWR analysis (Table 1). The adaptive bandwidth was selected to account for the unbalanced distribution of the surface monitors. The specific GWR model for PM2.5 estimation with the four explanatory variables is expressed as
PM 2.5 ~ AOD + PBLH + WS + VANUI
where PM2.5 is the daily ground-level PM2.5 measurement ( μ g / m 3 ); AOD is the mean AOD averaged from MODIS AOD products onboard the Terra and Aqua satellites (unitless); PBLH (m) and WS (m/s) are meteorological parameters (definitions in Section 2.2.1); and VANUI is the Vegetation Adjusted NTL Urban Index (unitless).
The spectral index VANUI is based on Zhang et al. [48]. It has proven to be effective in reducing the NTL saturation [49] by the combined use of NTL and vegetation information, as expressed below by
VANUI = ( 1 − NDVI ) × NTL
where NDVI is the MODIS Level 3 16-day NDVI value (unitless), and NTL is the normalized DMSP/OLS NTL value (unitless). The NDVI values are confined to (0, 1.0) to mask water bodies, while the normalized NTL values are accomplished by dividing the original NTL values by 63. Thus, VANUI has a value range of 0–1. VANUI values near 1 indicate core urban areas with little vegetation, whereas VANUI values close to 0 imply areas with dense vegetation cover [48].

2.3.3. Model Validation

To assess the role of VANUI in PM2.5 prediction, a GWR model without using VANUI (termed as GWR-basic, see Table 1) was constructed. Additionally, a GWR model with only NDVI data instead of VANUI (denoted as GWR-NDVI, see Table 1) was also constructed to specifically explore the contribution of DMSP/OLS NTL to PM2.5 prediction. For the convenience of description, the recommended GWR model with VANUI data, as given in Equation (1), is referred as GWR-VANUI.
To test the performance of the three specific models, a 10-fold cross validation was conducted. That is, the matched dataset in all sites was first randomly divided into 10 folds. Nine folds were used for model training, while the remaining one fold served for model testing [20]. This process was iterated 10 times until every site was tested. During the procedure, the root mean squared error (RMSE), the mean absolute error (MAE), the relative root mean squared error (RRMSE), and the relative mean absolute error (RMAE) were employed to evaluate the reliability of the GWR model predictions.

3. Results

3.1. Descriptive Statistics

Figure 3 shows the histograms of all related variables, expressed in frequency distribution. The descriptive statistics (e.g., mean, standard deviation (SD), maximum, minimum, and median) for the variables are summarized in Table 2. The annual average PM2.5 value in 2013 is 8.49 μg/m3, with a SD of 4.36 μg/m3. PM2.5 concentration shows a typical lognormal distribution. AOD has an overall mean value of 0.13, with a SD of 0.12. As expected, the frequency distribution of AOD is more similar to that of the PM2.5 concentration than to those of other variables. The correlation analysis verifies this point, with AOD having the highest Pearson’s coefficient of 0.51 with PM2.5. VANUI (0.52 ± 0.18) is close to a normal distribution, and similarly NDVI (0.45 ± 0.17) in the study region happens to exhibit a distribution similar to a normal distribution function. PBLH shows a lognormal distribution and has a broad value range, which is from 71 m to 1998 m. Surface wind speed (3.23 ± 1.64 m/s) tends to be a skewed normal distribution.
The seasonal changes for these variables is also analyzed and presented in Table 3. The mean PM2.5 concentrations during the winter (9.59 ± 5.62 μg/m3) and the summer (10.12 ± 5.05 μg/m3) are about 30% higher than those during the spring (7.56 ± 3.48 μg/m3) and the fall (7.75 ± 3.80 μg/m3). The mean AOD values are much higher in the spring (0.13 ± 0.10) and the summer (0.18 ± 0.14) than in the fall (0.07 ± 0.05) and the winter (0.07 ± 0.04). The highest mean value of VANUI is in the wintertime (0.68 ± 0.15) while the lowest mean VANUI value is in the summertime (0.44 ± 0.16). This may be partly due to the reduced vegetation cover as shown by NDVI (its mean value in winter decreases about 50% compared with that in summer), which results in relatively high values of VANUI according to Equation (2). The highest mean value of PBLH with the largest SD is observed in the summer (694.85 ± 525.03 m), which can be explained by strong solar radiation in the summer. On the contrary, the highest mean wind speed value is found in winter (4.94 ± 2.28 m/s).
Due to the shortage of the matched data records in the winter, the data was analyzed for two seasonal periods, a warm season (15 April–14 October) and a cold season (15 October–14 April), similar to that done in Lee, Liu, Coull, Schwartz, and Koutrakis [42]. The mean values of PM2.5 for the two seasonal analysis groups are close (8.73 ± 4.48 μg/m3 for the warm season, and 7.73 ± 3.89 μg/m3 for the cold season). By contrast, the mean value of AOD is much lower in the cold season (0.08 ± 0.06) than in the warm season (0.14 ± 0.12). Regional changes in rainfall and other weather parameters which increase or decrease the PM2.5 levels might be negatively affected by this choice but in the absence of more extensive valid winter data it was the best available option.
To avoid the potential problem of strong multicollinearity among the predictor variables, Pearson’s correlation coefficients were examined. The results show that the linear correlation coefficients between the predictors in individual GWR models are relatively low (Table 4). Thus, these predictors are suitable to be used together in GWR analysis. In fact, Fotheringham and Oshan [50] recently tested the sensitivity of GWR to multicollinearity and they found that GWR is very robust to the effects of multicollinearity.

3.2. Model Validation

Table 5 shows the results of cross validation for the GWR-basic, GWR-NDVI, and GWR-VANUI. According to the error data (represented by RMSE, MAE, RRMSE, and RMAE), GWR-basic performed the worst. In addition, the models performed relatively better for the warm season than for the cold season, which is consistent with the previous study of Kloog et al. [51]. Here, the GWR-basic is considered as the benchmark to evaluate the predictive capabilities of GWR-NDVI and GWR-VANUI.
By adding NDVI as a predictor to the GWR-basic model, the prediction performance of the GWR-NDVI was improved by 10.5%, 3.9%, 10.08% and 3.26% in terms of RMSE, MAE, RRMSE, and RMAE, respectively, for the warm season; and by 1.8%, 1.18%, 2.26% and 0.98% for the cold season, respectively. The results are in line with other recent studies [52,53,54], which all indicated that land use information such as NDVI can help to predict the PM2.5 concentration.
The VANUI, a combination of NDVI and NTL, was incorporated into the GWR-basic model to examine whether or not NTL can further improve the prediction accuracy of the PM2.5 concentration. Based on the cross-validation results, GWR-VANUI shows significant improvement over GWR-basic in performance for the warm season, with 17%, 8.44%, 17.65% and 8.7% decreases in RMSE, MAE, RRMSE, and RMAE, respectively; and GWR-VANUI also makes obvious improvement over GWR-NDVI in performance for the warm season, with decreases of the following percentages in RMSE: 7.26%, MAE: 4.73%, RRMSE: 8.41%, and RMAE: 5.62%. A similar trend is found in the cross-validation results for the cold season. Overall, the prediction accuracy of GWR-VANUI is much higher than those of the other two models (17% higher over GWR-basic and 7.26% higher over GWR-NDVI in terms of RMSE) for the warm season, while it is still higher than the latter (3.6% higher over GWR-basic and 1.83% higher over GWR-NDVI in terms of RMSE) for the cold season. In general, GWR-VANUI performs better than GWR-NDVI and GWR-basic. The better prediction performance of GWR-VANUI indicates that the NTL data is helpful for more accurately predicting the PM2.5 concentration.

3.3. Spatiotemporal Estimation of the PM2.5 Concentration

Figure 4 shows the spatial variability of PM2.5 in the warm season and cold season of 2013, estimated using the GWR-VANUI model. The predicted mean values of PM2.5 for the warm season range from 5.11 to 12.8 μg/m3, while the predicted mean values of PM2.5 for the cold season range from 3.69 to 8.85 μg/m3, much lower than that for the warm season. From the two maps, it can be seen that the high predicted mean values of PM2.5 concentration are distributed in the whole south part of New England, including CT, RI, and MA, in the warm season; however, high predicted mean values only appear in isolation in the areas of medium to large cities, such as Boston, Springfield, and Hartford, in the cold season. One possible explanation for the high level of PM2.5 in the warm season might be that the intense solar radiation, high temperature, and ample water vapor during summertime accelerate the formation of secondary particles [55].
The predicted annual mean values of PM2.5 in 2013 are shown in Figure 5a. The predicted values generally range from 4.7 μg/m3 near the ME border to 10 μg/m3 in New Haven, CT. By analyzing the change trend of the annual mean values of PM2.5 derived from all monitoring stations across New England during the period from 2000 to 2014, we find that the annual mean value decrease of PM2.5 during 2013–2014 (10.83%) is much larger than that during 2012–2013 (5.65%), and the general decreasing trend is relatively obvious during the entire period. This might be related to the tightening of emission controls in PM2.5. According to the newly revised National Ambient Air Quality Standards (NAAQS) issued in earlier 2013, the standard for annual PM2.5 was set to 12 μg/m3 instead of 15 μg/m3 [56].
Despite the fact that four New England states are ranked among the top ten healthiest states in the US [57], polluted air is found in southern New England but the pollution is still below the annual standard. Compared to heavily forested and rural areas in northern New England (e.g., VT and ME), highly urbanized and populous areas in southern New England, such as Boston, Springfield, Hartford, New Haven, Bridgeport, Stamford, and Providence appear to have higher levels of PM2.5. In addition, high PM2.5 values are more likely to appear along highways with heavy traffic and large cities (e.g., sections of I-91 and I-95 highways in southern New England), which are essentially high emission sources. The results match well with the fact that VANUI correlates with population density and energy consumption, indicating an evident association between the PM2.5 concentration and NTL data. It is interesting to see that within the urban areas of major cities in southern New England, the annual mean PM2.5 concentrations are obviously high as compared to their surrounding rural forest areas, but their spatial variations tend to be low. This might be because of the regional impacts of the transported PM2.5 pollution on these cities, as reported by a previous study [23].

4. Discussion

4.1. Comparison with an Available Product

To demonstrate the performance of the GWR-VANUI model, our results were also compared with one publicly available PM2.5 product, which can be downloaded from the Dalhousie University Atmospheric Composition Analysis Group Web site (http://fizz.phys.dal.ca/~atmos/martin/?page_id=140). This globally estimated annual mean PM2.5 product was based on the study of van Donkelaar et al. [58], which was produced by combining satellite-retrieved AOD with a chemical transport model and then adjusting the estimates to ground-level PM2.5 using GWR. To be identical to the legend of Figure 5a, the available product for 2013 with a spatial resolution of 0.1° × 0.1° was resized and replotted as shown in Figure 5b. In general, the GWR-VANUI estimated PM2.5 concentration map exhibits a spatial pattern similar to that of the publicly available product, but provides more details, especially in southern New England. Considering that these specific details may not be very clear on the map, a Pearson’s correlation analysis was conducted between the estimated values of PM2.5 and the observed values. The results show that the correlation coefficient r based on the Dalhousie University product is 0.11 lower than the Pearson’s correlation coefficient for the GWR-VANUI model results. The similarity in the results combined with the improved correlation and error parameters supports the hypothesis that the GWR-VANUI model results are reasonable and improve on the currently available alternative products.
Furthermore, the role of environmental background in estimating PM2.5 concentration was also examined. The entire New England was divided into two sub-regions: northern New England, which includes CT, MA and RI; and southern New England, which includes ME, NH and VT. The primary difference between these two sub-regions is that southern New England is more urbanized with a high population density and a low forest density, whereas northern New England is less urbanized with a low population density and a high forest density. With respect to the Pearson’s correlation gradient from south to north, the r value reduces 20.5% from 0.73 to 0.58 for the predicted data of the GWR-VANUI model, and in contrast, it drops 25.8% from 0.62 to 0.46 for the available product. Overall, our study shows that the incorporation of VANUI into GWR as a predictor variable can generate more promising results, especially for urbanized and populous areas, compared with the Dalhousie University product. The spatiotemporally resolved annual PM2.5 estimates generated from the GWR-VANUI model could provide valuable information for epidemiological studies such as chronic effects of air pollution at regional scales [59]. In addition, health risks of exposure to PM2.5 could also be assessed based on the annual spatial distribution maps of PM2.5 concentrations produced by our model, which could serve as strong support and rationales for the effective control of PM2.5 emissions as well as for the practical enactment of PM2.5 regulations [60].

4.2. Effect of NTL

In this study, three GWR models were constructed for predicting surface PM2.5 concentration across New England. The model prediction results indicate that DMSP/OLS NTL data combined with NDVI data (i.e., the VANUI) can be effective for more accurately estimating PM2.5 concentration, especially for core urban areas. To further investigate the impact of VANUI on PM2.5 concentration prediction, a data sequence comparison of annual mean values of PM2.5, VANUI, NTL, and NDVI at PM2.5 monitoring sites was conducted (Figure 6). Compared with NDVI and NTL data sequences visually, the general trend of VANUI is more similar to that of the PM2.5 concentration. In particular, VANUI exhibits high variability in Boston (0.70–0.59–0.67, with Site IDs of 250250002, 250250042, and 250250044, respectively. A detailed description of these monitor IDs can be found at [61]), matching well with the PM2.5 concentration values (7.96 μg/m3–7.35 μg/m3–7.82 μg/m3) at the same locations. However, there is not much change in the NDVI values (0.30–0.30–0.30). Conversely, in some rural areas such as New Hampshire, NDVI (0.74–0.49–0.49, with Site IDs of 330115001, 330131006, and 330150014, respectively) correlates better with the PM2.5 concentration values (6.25 μg/m3–7.09 μg/m3–7.10 μg/m3) than with the VANUI values (0.03–0.41–0.49). This is partly due to the fact reported in a previous study that VANUI is better at characterizing core urban variability, though it may not capture details well for cities where there is little variation in vegetation [48]. In addition, the use of VANUI successfully reduces the saturation issue confronted by NTL. For example, in core urban areas such as New Haven (Site IDs: 90090027 and 90091123), Boston (Site IDs: 250250002, 250250042, and 250250044), Springfield (Site IDs: 250130016 and 250132009), and Providence (Site IDs: 440070022), the normalized values of NTL have already been saturated to 1. However, the VANUI values within these regions show significant variability and the variations within these intra-urban monitors can be detectable. Pearson’s correlation coefficients between annual PM2.5 concentration and the three independent variables were also calculated to assess the prediction ability of VANUI. They are 0.70 for PM2.5 and VANUI, −0.59 for PM2.5 and NDVI, and 0.63 for PM2.5 and NTL, respectively. This further ascertains that DMSP/OLS NTL in combination with NDVI (i.e., the VANUI index) could be a better alternative to NDVI for more accurately estimating the PM2.5 concentration.

5. Conclusions

In this paper, a pilot study was undertaken to evaluate the potential of using DMSP/OLS NTL data for PM2.5 prediction. The case study focuses on the New England region, where both urban and rural settings are present. VANUI (an integrated index of NTL and NDVI), satellite-derived AOD measurement, and two meteorological factors were employed as predictor variables in GWR analysis for the estimation of the PM2.5 concentration at a regional scale. We compared the specific GWR model with VANUI (i.e., GWR-VANUI) to two other specific GWR models (GWR-basic and GWR-NDVI, both of which do not use NTL). The comparison results demonstrate that the GWR-VANUI can explain more information than the two GWR models without using NTL data. We found that including NTL data can significantly improve the performance of GWR for the warm season (GWR-VANUI performed 17% better than GWR-basic and 7.26% better than GWR-NDVI in terms of RMSE), while its improvements are less obvious for the cold season (GWR-VANUI performed 3.6% better than GWR-basic and 1.83% better than GWR-NDVI in terms of RMSE). This work suggests that using NTL combined with NDVI is helpful in assessing ground-based PM2.5 concentration.
Likewise, the spatial distribution of the predicted PM2.5 concentration indicates the value of using DMSP/OLS NTL data for air quality monitoring. Higher concentrations of PM2.5 expectedly occur in urbanized and populated areas and along interstate highways, while lower levels of PM2.5 appear in less urbanized or densely forested areas. Furthermore, the comparison of data sequences of annual mean values of PM2.5 and three related variables at monitoring sites shows that the integrated use of NTL and NDVI data (as the VANUI index) is a better choice for predicting PM2.5 concentration, especially in core urban areas, where more details can be found in the predicted PM2.5 surface map. Therefore, it can be concluded that the DMSP/OLS NTL imagery can be used as a valuable dataset for more accurately predicting regional PM2.5 pollution, and this study provides supportive evidence useful for its future application in air quality monitoring.
There are still several aspects that need further improvement in future work. One is the relatively coarse spatial resolution of the satellite-retrieved AOD product used in the study. Another issue is that the capability of current VANUI is limited by the 6-bit radiometric scale of NTL [48]. With the newly released Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the Suomi National Polar-orbiting Partnership (S-NPP) spacecraft, which has a spatial resolution of 6 km for aerosol retrievals and a broader radiometric scale of 14-bit, it is expected for new opportunities to further reduce the prediction errors of PM2.5 concentration. Moreover, the sparse measurements in winter as well as other additional factors such as rainfall tend to limit the model prediction. In future research, we will attempt to incorporate other influential predictors into a mixed-effects model [62], which could generate daily PM2.5 predictions to minimize the bias.

Acknowledgments

We are grateful for the helpful comments and suggestions offered by the two anonymous reviewers for improving the quality of this paper. We also thank the MODIS Science Data Support Team and the Earth Observing System for processing, maintaining and distributing the MODIS data.

Author Contributions

Xueke Li and Chuanrong Zhang conceived and designed the framework of this research. Xueke Li performed the data processing and wrote the draft of the manuscript. Chuanrong Zhang and Weidong Li revised and edited the manuscript. Kai Liu gave advice for writing the paper.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar] [CrossRef]
  2. Kaufman, Y.J.; Tanre, D.; Boucher, O. A satellite view of aerosols in the climate system. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef] [PubMed]
  3. Dockery, D.W.; Pope, C.A.; Xu, X.; Spengler, J.D.; Ware, J.H.; Fay, M.E.; Ferris, B.G.J.; Speizer, F.E. An association between air pollution and mortality in six U.S. Cities. N. Engl. J. Med. 1993, 329, 1753–1759. [Google Scholar] [CrossRef] [PubMed]
  4. Pope, C.A. Epidemiology of fine particulate air pollution and human health: Biologic mechanisms and who’s at risk? Environ. Health Perspect. 2000, 108, 713–723. [Google Scholar] [CrossRef] [PubMed]
  5. Dominici, F.; Peng, R.D.; Bell, M.L.; Pham, L.; McDermott, A.; Zeger, S.L.; Samet, J.M. Fine particulate air pollution and hospital admission for cardiovascular and respiratory diseases. JAMA 2006, 295, 1127–1134. [Google Scholar] [CrossRef] [PubMed]
  6. Miller, K.A.; Siscovick, D.S.; Sheppard, L.; Shepherd, K.; Sullivan, J.H.; Anderson, G.L.; Kaufman, J.D. Long-term exposure to air pollution and incidence of cardiovascular events in women. N. Engl. J. Med. 2007, 356, 447–458. [Google Scholar] [CrossRef] [PubMed]
  7. Rice, M.B.; Ljungman, P.L.; Wilker, E.H.; Gold, D.R.; Schwartz, J.D.; Koutrakis, P.; Washko, G.R.; O’Connor, G.T.; Mittleman, M.A. Short-term exposure to air pollution and lung function in the framingham heart study. Am. J. Respir. Crit. Care Med. 2013, 188, 1351–1357. [Google Scholar] [CrossRef] [PubMed]
  8. Rice, M.B.; Ljungman, P.L.; Wilker, E.H.; Dorans, K.S.; Gold, D.R.; Schwartz, J.; Koutrakis, P.; Washko, G.R.; O’Connor, G.T.; Mittleman, M.A.; et al. Long-term exposure to traffic emissions and fine particulate matter and lung function decline in the framingham heart study. Am. J. Respir. Crit. Care Med. 2015, 191, 656–664. [Google Scholar] [CrossRef] [PubMed]
  9. Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Kahn, R.; Levy, R.; Verduzco, C.; Villeneuve, P.J. Global estimates of ambient fine particulate matter concentrations from satellite-based aerosol optical depth: Development and application. Environ. Health Perspect. 2010, 118, 847–855. [Google Scholar] [CrossRef] [PubMed]
  10. Engel-Cox, J.A.; Hoff, R.M.; Haymet, A.D.J. Recommendations on the use of satellite remote-sensing data for urban air quality. J. Air Waste Manag. Assoc. 2004, 54, 1360–1371. [Google Scholar] [CrossRef] [PubMed]
  11. Gupta, P.; Christopher, S.A.; Wang, J.; Gehrig, R.; Lee, Y.; Kumar, N. Satellite remote sensing of particulate matter and air quality assessment over global cities. Atmos. Environ. 2006, 40, 5880–5892. [Google Scholar] [CrossRef]
  12. Hoff, R.M.; Christopher, S.A. Remote sensing of particulate pollution from space: Have we reached the promised land? J. Air Waste Manag. Assoc. 2009, 59, 645–675. [Google Scholar] [PubMed]
  13. Liu, Y.; Franklin, M.; Kahn, R.; Koutrakis, P. Using aerosol optical thickness to predict ground-level PM2.5 concentrations in the st. Louis area: A comparison between misr and MODIS. Remote Sens. Environ. 2007, 107, 33–44. [Google Scholar] [CrossRef]
  14. Liu, Y.; Paciorek, C.J.; Koutrakis, P. Estimating regional spatial and temporal variability of PM2.5 concentrations using satellite data, meteorology, and land use information. Environ. Health Perspect. 2009, 117, 886–892. [Google Scholar] [CrossRef] [PubMed]
  15. Slater, J.F.; Dibb, J.E.; Campbell, J.W.; Moore, T.S. Physical and chemical properties of surface and column aerosols at a rural new england site during MODIS overpass. Remote Sens. Environ. 2004, 92, 173–180. [Google Scholar] [CrossRef]
  16. You, W.; Zang, Z.; Pan, X.; Zhang, L.; Chen, D. Estimating PM2.5 in xi’an, china using aerosol optical depth: A comparison between the MODIS and misr retrieval models. Sci. Total Environ. 2015, 505, 1156–1165. [Google Scholar] [CrossRef] [PubMed]
  17. Kumar, K.R.; Sivakumar, V.; Yin, Y.; Reddy, R.R.; Kang, N.; Diao, Y.; Adesina, A.J.; Yu, X. Long-term (2003–2013) climatological trends and variations in aerosol optical parameters retrieved from MODIS over three stations in south africa. Atmos. Environ. 2014, 95, 400–408. [Google Scholar] [CrossRef]
  18. Remer, L.A.; Kaufman, Y.J.; Tanré, D.; Mattoo, S.; Chu, D.A.; Martins, J.V.; Li, R.R.; Ichoku, C.; Levy, R.C.; Kleidman, R.G.; et al. The MODIS aerosol algorithm, products, and validation. J. Atmos. Sci. 2005, 62, 947–973. [Google Scholar] [CrossRef]
  19. Chu, D.A.; Tsai, T.-C.; Chen, J.-P.; Chang, S.-C.; Jeng, Y.-J.; Chiang, W.-L.; Lin, N.-H. Interpreting aerosol lidar profiles to better estimate surface PM2.5 for columnar aod measurements. Atmos. Environ. 2013, 79, 172–187. [Google Scholar] [CrossRef]
  20. Hu, X.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G., Jr.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern U.S. using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
  21. Kloog, I.; Nordio, F.; Coull, B.A.; Schwartz, J. Incorporating local land use regression and satellite aerosol optical depth in a hybrid model of spatiotemporal PM2.5 exposures in the mid-atlantic states. Environ. Sci. Technol. 2012, 46, 11913–11921. [Google Scholar] [CrossRef] [PubMed]
  22. Koelemeijer, R.B.A.; Homan, C.D.; Matthijsen, J. Comparison of spatial and temporal variations of aerosol optical thickness and particulate matter over europe. Atmos. Environ. 2006, 40, 5304–5315. [Google Scholar] [CrossRef]
  23. Lee, H.J.; Coull, B.A.; Bell, M.L.; Koutrakis, P. Use of satellite-based aerosol optical depth and spatial clustering to predict ambient PM2.5 concentrations. Environ. Res. 2012, 118, 8–15. [Google Scholar] [CrossRef] [PubMed]
  24. Liu, Y.; Sarnat, J.A.; Kilaru, V.; Jacob, D.J.; Koutrakis, P. Estimating ground-level PM2.5 in the Eastern United States using satellite remote sensing. Environ. Sci. Technol. 2005, 39, 3269–3278. [Google Scholar] [CrossRef] [PubMed]
  25. Zou, B.; Pu, Q.; Bilal, M.; Weng, Q.; Zhai, L.; Nichol, J.E. High-resolution satellite mapping of fine particulates based on geographically weighted regression. IEEE Geosci. Remote Sens. Lett. 2016, 13, 495–499. [Google Scholar] [CrossRef]
  26. Elvidge, C.; Baugh, K.; Hobson, V.; Kihn, E.; Kroehl, H.; Davis, E.; Cocero, D. Satellite inventory of human settlements using nocturnal radiation emissions: A contribution for the global toolchest. Glob. Chang. Biol. 1997, 3, 387–395. [Google Scholar] [CrossRef]
  27. Sutton, P.C.; Elvidge, C.; Obremski, T. Building and evaluating models to estimate ambient population density. Photogramm. Eng. Remote Sens. 2003, 69, 545–553. [Google Scholar] [CrossRef]
  28. Yuyu, Z.; Steven, J.S.; Kaiguang, Z.; Marc, I.; Allison, T.; Ben, B.-L.; Ghassem, R.A.; Xuesong, Z.; Chunyang, H.; Christopher, D.E.; et al. A global map of urban extent from nightlights. Environ. Res. Lett. 2015, 10, 054011. [Google Scholar]
  29. Zhou, N.; Hubacek, K.; Roberts, M. Analysis of spatial patterns of urban growth across south asia using dmsp-ols nighttime lights data. Appl. Geogr. 2015, 63, 292–303. [Google Scholar] [CrossRef]
  30. Zhou, Y.; Smith, S.J.; Elvidge, C.D.; Zhao, K.; Thomson, A.; Imhoff, M. A cluster-based method to map urban area from dmsp/ols nightlights. Remote Sens. Environ. 2014, 147, 173–185. [Google Scholar] [CrossRef]
  31. Li, R.; Liu, X.; Li, X. Estimation of the PM2.5 pollution levels in beijing based on nighttime light data from the defense meteorological satellite program-operational linescan system. Atmosphere 2015, 6, 607–622. [Google Scholar] [CrossRef]
  32. Xu, Z.; Xia, X.; Liu, X.; Qian, Z. Combining dmsp/ols nighttime light with echo state network for prediction of daily PM2.5 average concentrations in shanghai, china. Atmosphere 2015, 6, 1507–1520. [Google Scholar] [CrossRef]
  33. Fotheringham, A.S.; Brunsdon, C.; Charlton, M. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley & Sons: New York, NY, USA, 2002. [Google Scholar]
  34. Redman, C.; Foster, D.R. Agrarian Landscapes in Transition: Comparisons of Long-Term Ecological & Cultural Change; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
  35. US Environmental Protection Agency. Air Quality System Data Mart. Available online: http://www.epa.gov/ttn/airs/aqsdatamart (accessed on 14 June 2017).
  36. The Phase 2 North America Land Data Assimilation System (NLDAS-2). Available online: https://ldas.gsfc.nasa.gov/nldas/NLDAS2forcing.php (accessed on 14 June 2017).
  37. Atmosphere Archive and Distribution System. Available online: http://ladsweb.nascom.nasa.gov (accessed on 14 June 2017).
  38. Remer, L.A.; Kleidman, R.G.; Levy, R.C.; Kaufman, Y.J.; Tanré, D.; Mattoo, S.; Martins, J.V.; Ichoku, C.; Koren, I.; Yu, H.; et al. Global aerosol climatology from the MODIS satellite sensors. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
  39. Defense Meteorological Satellite Program (DMSP). Available online: https://ngdc.noaa.gov/eog/dmsp.html (accessed on 14 June 2017).
  40. National Aeronautics and Space Administration (NASA)’s Earth Observations (NEO). Available online: https://neo.sci.gsfc.nasa.gov/ (accessed on 14 June 2017).
  41. Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
  42. Lee, H.; Liu, Y.; Coull, B.; Schwartz, J.; Koutrakis, P. A novel calibration approach of MODIS aod data to predict PM2.5 concentrations. Atmos. Chem. Phys. 2011, 11, 7991–8002. [Google Scholar] [CrossRef]
  43. Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
  44. Lin, G.; Fu, J.; Jiang, D.; Hu, W.; Dong, D.; Huang, Y.; Zhao, M. Spatio-temporal variation of PM2.5 concentrations and their relationship with geographic and socioeconomic factors in china. Int. J. Environ. Res. Public Health 2014, 11, 173–186. [Google Scholar] [CrossRef] [PubMed]
  45. Song, W.; Jia, H.; Huang, J.; Zhang, Y. A satellite-based geographically weighted regression model for regional PM2.5 estimation over the pearl river delta region in china. Remote Sens. Environ. 2014, 154, 1–7. [Google Scholar] [CrossRef]
  46. Wang, K.; Zhang, C.; Li, W. Predictive mapping of soil total nitrogen at a regional scale: A comparison between geographically weighted regression and cokriging. Appl. Geogr. 2013, 42, 73–85. [Google Scholar] [CrossRef]
  47. Zhang, C.; Li, W.; Civco, D. Application of geographically weighted regression to fill gaps in slc-off landsat etm+ satellite imagery. Int. J. Remote Sens. 2014, 35, 7650–7672. [Google Scholar] [CrossRef]
  48. Zhang, Q.; Schaaf, C.; Seto, K.C. The vegetation adjusted ntl urban index: A new approach to reduce saturation and increase variation in nighttime luminosity. Remote Sens. Environ. 2013, 129, 32–41. [Google Scholar] [CrossRef]
  49. Elvidge, C.D.; Cinzano, P.; Pettit, D.R.; Arvesen, J.; Sutton, P.; Small, C.; Nemani, R.; Longcore, T.; Rich, C.; Safran, J.; et al. The nightsat mission concept. Int. J. Remote Sens. 2007, 28, 2645–2670. [Google Scholar] [CrossRef]
  50. Fotheringham, A.S.; Oshan, T.M. Geographically weighted regression and multicollinearity: Dispelling the myth. J. Geogr. Syst. 2016, 18, 303–329. [Google Scholar] [CrossRef]
  51. Kloog, I.; Koutrakis, P.; Coull, B.A.; Lee, H.J.; Schwartz, J. Assessing temporally and spatially resolved PM2.5 exposures for epidemiological studies using satellite aerosol optical depth measurements. Atmos. Environ. 2011, 45, 6267–6275. [Google Scholar] [CrossRef]
  52. Di, Q.; Kloog, I.; Koutrakis, P.; Lyapustin, A.; Wang, Y.; Schwartz, J. Assessing PM2.5 exposures with high spatiotemporal resolution across the continental United States. Environ. Sci. Technol. 2016, 50, 4712–4721. [Google Scholar] [CrossRef] [PubMed]
  53. Lee, M.; Kloog, I.; Chudnovsky, A.; Lyapustin, A.; Wang, Y.; Melly, S.; Coull, B.; Koutrakis, P.; Schwartz, J. Spatiotemporal prediction of fine particulate matter using high-resolution satellite images in the southeastern US 2003–2011. J. Expo. Sci. Environ. Epidemiol. 2016, 26, 377–384. [Google Scholar] [CrossRef] [PubMed]
  54. Ma, L.; Wu, J.; Li, W.; Peng, J.; Liu, H. Evaluating saturation correction methods for dmsp/ols nighttime light data: A case study from china’s cities. Remote Sens. 2014, 6, 9853–9872. [Google Scholar] [CrossRef]
  55. Hu, X.; Waller, L.A.; Lyapustin, A.; Wang, Y.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G., Jr.; Estes, S.M.; Quattrochi, D.A.; Puttaswamy, S.J.; et al. Estimating ground-level PM2.5 concentrations in the Southeastern United States using maiac aod retrievals and a two-stage model. Remote Sens. Environ. 2014, 140, 220–232. [Google Scholar] [CrossRef]
  56. Air quality: Epa’s 2013 Changes to the Particulate Matter (Pm) Standard. Available online: http://www.nationalaglawcenter.org/wp-content/uploads/assets/crs/RL33254.pdf (accessed on 3 May 2017).
  57. America’s Health Rankings. Available online: http://cdnfiles.americashealthrankings.org/SiteFiles/Reports/Americas-Health-Rankings-2012-v1.pdf (accessed on 3 May 2017).
  58. van Donkelaar, A.; Martin, R.V.; Spurr, R.J.D.; Burnett, R.T. High-resolution satellite-derived PM2.5 from optimal estimation and geographically weighted regression over north america. Environ. Sci. Technol. 2015, 49, 10482–10491. [Google Scholar] [CrossRef] [PubMed]
  59. Kloog, I.; Coull, B.A.; Zanobetti, A.; Koutrakis, P.; Schwartz, J.D. Acute and chronic effects of particles on hospital admissions in new-england. PLoS ONE 2012, 7, e34664. [Google Scholar] [CrossRef] [PubMed]
  60. Peng, J.; Chen, S.; Lü, H.; Liu, Y.; Wu, J. Spatiotemporal patterns of remotely sensed PM2.5 concentration in china from 1999 to 2011. Remote Sens. Environ. 2016, 174, 109–121. [Google Scholar] [CrossRef]
  61. AirData Download Files Documentation. Available online: https://aqsdr1.epa.gov/aqsweb/aqstmp/airdata/FileFormats.html (accessed on 14 June 2017).
  62. Kloog, I.; Chudnovsky, A.A.; Just, A.C.; Nordio, F.; Koutrakis, P.; Coull, B.A.; Lyapustin, A.; Wang, Y.; Schwartz, J. A new hybrid spatio-temporal model for estimating daily multi-year PM2.5 concentrations across northeastern USA using high resolution aerosol optical depth data. Atmos. Environ. 2014, 95, 581–590. [Google Scholar] [CrossRef]
Remotesensing 09 00620 g001 550
Figure 1. Map of the study area (The islands of Martha’s Vineyard, MA and town of Nantucket, MA are not shown here). The grid cell shown in the map is of 10 km × 10 km resolution.
Figure 1. Map of the study area (The islands of Martha’s Vineyard, MA and town of Nantucket, MA are not shown here). The grid cell shown in the map is of 10 km × 10 km resolution.
Remotesensing 09 00620 g001
Remotesensing 09 00620 g002 550
Figure 2. Flowchart outlining the PM2.5 estimation procedures in this study. The highlighted box indicates the three different scenarios for constructing the prediction model with geographically weighted regression (GWR). With other variables (e.g., aerosol optical depth (AOD) and meteorological parameters) being the same, the main difference of the three specific GWR models lies in the incorporation of land use information: (1) GWR model without normalized difference vegetation index (NDVI) and nighttime light (NTL) data (termed as GWR-basic), (2) GWR model with NDVI data (GWR-NDVI), and (3) GWR model with vegetation adjusted NTL urban index (VANUI) data (including NDVI and NTL) (GWR-VANUI).
Figure 2. Flowchart outlining the PM2.5 estimation procedures in this study. The highlighted box indicates the three different scenarios for constructing the prediction model with geographically weighted regression (GWR). With other variables (e.g., aerosol optical depth (AOD) and meteorological parameters) being the same, the main difference of the three specific GWR models lies in the incorporation of land use information: (1) GWR model without normalized difference vegetation index (NDVI) and nighttime light (NTL) data (termed as GWR-basic), (2) GWR model with NDVI data (GWR-NDVI), and (3) GWR model with vegetation adjusted NTL urban index (VANUI) data (including NDVI and NTL) (GWR-VANUI).
Remotesensing 09 00620 g002
Remotesensing 09 00620 g003 550
Figure 3. Histograms of all related variables used in the study.
Figure 3. Histograms of all related variables used in the study.
Remotesensing 09 00620 g003
Remotesensing 09 00620 g004 550
Figure 4. Spatial distribution maps of mean values of PM2.5 in the warm season (a) and the cold season (b) of 2013, estimated using the GWR-VANUI model.
Figure 4. Spatial distribution maps of mean values of PM2.5 in the warm season (a) and the cold season (b) of 2013, estimated using the GWR-VANUI model.
Remotesensing 09 00620 g004
Remotesensing 09 00620 g005 550
Figure 5. Spatial distribution maps of the GWR-VANUI predicted annual mean values of PM2.5 concentration in 2013 (a) and the publicly available annual mean PM2.5 product in 2013 (b) (downloaded from the website http://fizz.phys.dal.ca/~atmos/martin/?page_id=140).
Figure 5. Spatial distribution maps of the GWR-VANUI predicted annual mean values of PM2.5 concentration in 2013 (a) and the publicly available annual mean PM2.5 product in 2013 (b) (downloaded from the website http://fizz.phys.dal.ca/~atmos/martin/?page_id=140).
Remotesensing 09 00620 g005
Remotesensing 09 00620 g006 550
Figure 6. Data sequence comparison of annual means values of PM2.5, Vegetation Adjust NTL Urban Index (VANUI), nighttime light (NTL), and Normalized Difference Vegetation Index (NDVI) at PM2.5 monitoring sites located in New England.
Figure 6. Data sequence comparison of annual means values of PM2.5, Vegetation Adjust NTL Urban Index (VANUI), nighttime light (NTL), and Normalized Difference Vegetation Index (NDVI) at PM2.5 monitoring sites located in New England.
Remotesensing 09 00620 g006
Table
Table 1. Description of the three specific GWR models for estimating the daily PM2.5 concentration.
Table 1. Description of the three specific GWR models for estimating the daily PM2.5 concentration.
GWR ModelModel Predictors *
GWR-basicAOD, PBLH, WS
GWR-NDVIAOD, PBLH, WS, NDVI
GWR-VANUIAOD, PBLH, WS, VANUI
* AOD: aerosol optical depth. PBLH: planetary boundary layer height (m). WS: wind speed (m/s). NDVI: normalized difference vegetation index. VANUI: vegetation adjusted NTL urban index, which integrates NTL and NDVI.
Table
Table 2. Descriptive statistics for all related variables.
Table 2. Descriptive statistics for all related variables.
MeanStd. Dev.MinMaxMedian
PM2.5 (μg/m3)8.494.362.129.797.36
Aerosol optical depth0.130.120.0010.670.09
Vegetation adjusted NTL urban index0.520.180.140.980.50
Normalized difference vegetation index0.450.170.010.830.45
Planetary boundary layer height (m)420.17357.0171.121997.97270.32
Wind speed (m/s)3.231.640.01810.533.00
Table
Table 3. Seasonal summary statistics for all related variables.
Table 3. Seasonal summary statistics for all related variables.
Spring (N = 543)MeanStd. Dev.MinMaxMedian
PM2.5 (μg/m3)7.563.482.1524.966.70
Aerosol optical depth0.130.100.0010.570.09
Vegetation adjusted NTL urban index0.550.170.150.880.55
Normalized difference vegetation index0.420.150.110.760.41
Planetary boundary layer height (m)469.13424.4072.131997.97285.18
Wind speed (m/s)3.171.860.01810.532.89
Summer (N = 467)MeanStd. Dev.MinMaxMedian
PM2.5 (μg/m3)10.125.052.529.799.25
Aerosol optical depth0.180.140.0010.670.15
Vegetation adjusted NTL urban index0.440.160.140.960.41
Normalized difference vegetation index0.540.160.030.830.54
Planetary boundary layer height (m)694.85525.03105.471417.28727.27
Wind speed (m/s)2.891.050.406.682.83
Fall (N = 427)MeanStd. Dev.MinMaxMedian
PM2.5 (μg/m3)7.753.802.125.107.04
Aerosol optical depth0.070.050.0010.360.06
Vegetation adjusted NTL urban index0.550.190.140.980.54
Normalized difference vegetation index0.410.170.010.740.38
Planetary boundary layer height (m)465.74373.1071.121583.02273.92
Wind speed (m/s)3.611.730.1810.143.24
Winter (N = 180)MeanStd. Dev.MinMaxMedian
PM2.5 (μg/m3)9.595.623.2120.206.75
Aerosol optical depth0.070.040.0230.200.08
Vegetation adjusted NTL urban index0.680.150.460.980.70
Normalized difference vegetation index0.270.130.010.500.26
Planetary boundary layer height (m)310.99173.9472.511016.89256.89
Wind speed (m/s)4.942.282.198.533.74
Table
Table 4. Pearson’s correlation coefficient calculated among predictor variables.
Table 4. Pearson’s correlation coefficient calculated among predictor variables.
VANUINDVIHPBLWS
AOD0.0250.034−0.197−0.135
VANUI−0.879 *0.1050.074
NDVI−0.180−0.117
HPBL0.295
* Note that VANUI and NDVI are strongly negatively correlated, but they were not used in the same GWR model.
Table
Table 5. Ten-fold cross validation results for GWR-basic, GWR-NDVI, and GWR-VANUI.
Table 5. Ten-fold cross validation results for GWR-basic, GWR-NDVI, and GWR-VANUI.
SeasonError IndexGWR-BasicGWR-NDVIGWR-VANUI
ValueValueImprovement (%) over GWR-BasicValueImprovement (%) over GWR-BasicImprovement (%) over GWR-NDVI
Warm seasonRMSE21.7910.51.66177.26
MAE1.541.483.91.418.444.73
RRMSE (%)11.910.710.089.817.658.41
RMAE (%)9.28.93.268.48.75.62
Cold seasonRMSE2.222.181.82.143.61.83
MAE1.71.681.181.652.941.79
RRMSE (%)13.3132.2612.83.761.54
RMAE (%)10.210.10.989.83.922.97

Share and Cite

MDPI and ACS Style

Li, X.; Zhang, C.; Li, W.; Liu, K. Evaluating the Use of DMSP/OLS Nighttime Light Imagery in Predicting PM2.5 Concentrations in the Northeastern United States. Remote Sens. 2017, 9, 620. https://doi.org/10.3390/rs9060620

AMA Style

Li X, Zhang C, Li W, Liu K. Evaluating the Use of DMSP/OLS Nighttime Light Imagery in Predicting PM2.5 Concentrations in the Northeastern United States. Remote Sensing. 2017; 9(6):620. https://doi.org/10.3390/rs9060620

Chicago/Turabian Style

Li, Xueke, Chuanrong Zhang, Weidong Li, and Kai Liu. 2017. "Evaluating the Use of DMSP/OLS Nighttime Light Imagery in Predicting PM2.5 Concentrations in the Northeastern United States" Remote Sensing 9, no. 6: 620. https://doi.org/10.3390/rs9060620

APA Style

Li, X., Zhang, C., Li, W., & Liu, K. (2017). Evaluating the Use of DMSP/OLS Nighttime Light Imagery in Predicting PM2.5 Concentrations in the Northeastern United States. Remote Sensing, 9(6), 620. https://doi.org/10.3390/rs9060620

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop