Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment
Abstract
:1. Introduction
1.1. Motivation
1.2. State of the Art
1.3. Problems with Thermal Infrared Data
1.4. Research Questions
2. Materials and Methods
2.1. Data
2.2. Site Description
2.3. Methods
2.3.1. Land Surface Temperature
2.3.2. Land Use/Land Cover
2.3.3. Administrative and Residential Boundaries
2.3.4. Averaging Land Surface Temperature and Spatial Land Cover Fractions
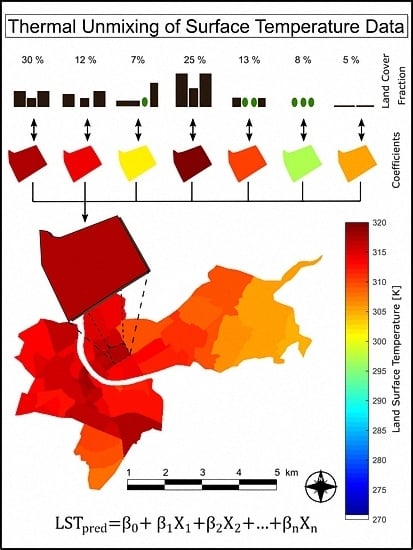
2.3.5. Multiple Linear Regression Analysis
3. Results
3.1. Land Surface Temperature and Land Use/Land Cover
3.2. Multiple Linear Regression Analysis
4. Discussion
4.1. Thermal Infrared Remote Sensing Problems
4.2. Connection of Land Surface Temperature, Vegetation and Land Use/Land Cover
4.2.1. Spatial Distribution of Land Surface Temperature
4.2.2. Multiple Linear Regression Analysis
4.2.3. Class-Specific Dependencies
5. Conclusions
- Application of MLR analysis for the interpretation of geographic data, especially regarding the growing datasets and the handling of big data
- Modeling the influence of changing land cover types on the LST and quantifying these effects
- Knowledge about the seasonal behavior of the connection between land cover and LST
- Informative figures describing the connection between land cover and LST, which can be adapted to other cities to show the cause and patterns of urban heat island issues and make it easy accessible to laymen
Acknowledgments
Author Contributions
Conflicts of Interest
References
- World Health Organization (WHO). Global Health Observatory Data Repository. Available online: http://apps.who.int/gho/data/node.main.nURBPOP?lang=en (accessed on 13 December 2016).
- López-Moreno, E.; Oyeyinka, O.; Mboup, G. Urban Trends. In State of the World’s Cities 2010/2011; Earthscan: London, UK, 2010; p. 220. [Google Scholar]
- Höppe, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Matzarakis, A.; Mayer, H.; Iziomon, M.G. Applications of a universal thermal index: Physiological equivalent temperature. Int. J. Biometeorol. 1999, 43, 76–84. [Google Scholar] [CrossRef] [PubMed]
- Honjo, T. Thermal comfort in outdoor environment. Glob. Environ. Res. 2009, 13, 43–47. [Google Scholar]
- Matzarakis, A.; Endler, C. Climate change and thermal bioclimate in cities: Impacts and options for adaptation in Freiburg, Germany. Int. J. Biometeorol. 2010, 54, 479–483. [Google Scholar] [CrossRef] [PubMed]
- Black, E.; Blackburn, M.; Harrison, G.; Hoskins, B.; Methven, J. Factors contributing to the summer 2003 European heatwave. Weather 2004, 59, 217–223. [Google Scholar] [CrossRef]
- Robine, J.-M.; Cheung, S.L.; Roy, S.L.; Oyen, H.V.; Griffiths, C.; Michel, J.-P.; Herrmann, F.R. Death toll exceeded 70,000 in Europe during the summer of 2003. C. R. Biol. 2008, 331, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Vicedo-Cabrera, A.M.; Ragettli, M.S.; Schindler, C.; Roosli, M. Excess mortality during the warm summer of 2015 in Switzerland. Swiss Med. Wkly. 2016, 146, 12. [Google Scholar] [CrossRef] [PubMed]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Karl, T.R.; Trenberth, K.E. Modern global climate change. Science 2003, 302, 1719–1723. [Google Scholar] [CrossRef] [PubMed]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Gerstengarbe, F.-W.; Werner, P.C. Katalog der Großwetterlagen Europas nach Paul Hess und Helmuth Brezowsky (1881–2004); Potsdam Institude for Climate Impact Research (PIK): Potsdam, Germany, 2005. [Google Scholar]
- Frey, C.M.; Parlow, E. Flux measurements in Cairo. Part 2: On the determination of the spatial radiation and energy balance using ASTER satellite data. Remote Sens. 2012, 4, 2635–2660. [Google Scholar] [CrossRef]
- Jin, M.S.; Kessomkiat, W.; Pereira, G. Satellite-observed urbanization characters in Shanghai, China: Aerosols, urban heat island effect, and land–atmosphere interactions. Remote Sens. 2011, 3, 83–99. [Google Scholar] [CrossRef]
- Rotach, M.W.; Vogt, R.; Bernhofer, C.; Batchvarova, E.; Christen, A.; Clappier, A.; Feddersen, B.; Gryning, S.E.; Martucci, G.; Mayer, H.; et al. BUBBLE—An urban boundary layer meteorology project. Theor. Appl. Climatol. 2005, 81, 231–261. [Google Scholar] [CrossRef]
- Parlow, E.; Vogt, R.; Feigenwinter, C. The urban heat island of Basel—Seen from different perspectives. DIE ERDE J. Geogr. Soc. Berl. 2014, 145, 96–110. [Google Scholar] [CrossRef]
- Oke, T.R. Canyon geometry and the nocturnal urban heat island: Comparison of scale model and field observations. J. Climatol. 1981, 1, 237–254. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Oke, T.R.; Johnson, G.T.; Steyn, D.G.; Watson, I.D. Simulation of surface urban heat islands under ‘ideal‘ conditions at night Part 2: Diagnosis of causation. Bound. Layer Meteorol. 1991, 56, 339–358. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Howard, L. The Climate of London; W. Phillips: London, UK, 1818. [Google Scholar]
- Ren, C.; Ng, E.; Katzschner, L. Urban climatic map studies: A review. Int. J. Climatol. 2011, 31, 2213–2233. [Google Scholar] [CrossRef]
- Eliasson, I. The use of climate knowledge in urban planning. Landsc. Urban Plan. 2000, 48, 31–44. [Google Scholar] [CrossRef]
- Mayer, H.; Holst, J.; Dostal, P.; Imbery, F.; Schindler, D. Human thermal comfort in summer within an urban street canyon in Central Europe. Meteorol. Z. 2008, 17, 241–250. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Feigenwinter, C.; Triantakonstantis, D.; Penyevskiy, I.; Tal, A.; Parlow, E.; Fleishman, G.; Düzgün, S.; Esch, T.; Marconcini, M. A conceptual list of indicators for urban planning and management based on Earth observation. ISPRS Int. J. Geo-Inf. 2014, 3, 980–1002. [Google Scholar] [CrossRef]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm. Remote Sens. 2009, 64, 335–344. [Google Scholar] [CrossRef]
- Voogt, J.A. Image representations of complete urban surface temperatures. Geocarto Int. 2000, 15, 21–32. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Effects of urban surface geometry on remotely-sensed surface temperature. Int. J. Remote Sens. 1998, 19, 895–920. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Dash, P.; Göttsche, F.-M.; Olesen, F.-S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice—Current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, B.-H.; Wu, H.; Ren, H.; Yan, G.; Wan, Z.; Trigo, I.F.; Sobrino, J.A. Satellite-derived land surface temperature: Current status and perspectives. Remote Sens. Environ. 2013, 131, 14–37. [Google Scholar] [CrossRef]
- Dousset, B.; Gourmelon, F.; Laaidi, K.; Zeghnoun, A.; Giraudet, E.; Bretin, P.; Mauri, E.; Vandentorren, S. Satellite monitoring of summer heat waves in the Paris metropolitan area. Int. J. Climatol. 2011, 31, 313–323. [Google Scholar] [CrossRef]
- Bechtel, B. Multitemporal Landsat data for urban heat island assessment and classification of local climate zones. In Joint Urban Remote Sensing Event (JURSE); IEEE: Munich, Germany, 2011; pp. 129–132. [Google Scholar]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index—Radiometric temperature relationship. Remote Sens. Environ. 2003, 85, 429–440. [Google Scholar] [CrossRef]
- Zhan, W.; Chen, Y.; Zhou, J.; Wang, J.; Liu, W.; Voogt, J.; Zhu, X.; Quan, J.; Li, J. Disaggregation of remotely sensed land surface temperature: Literature survey, taxonomy, issues, and caveats. Remote Sens. Environ. 2013, 131, 119–139. [Google Scholar] [CrossRef]
- Weng, Q.; Fu, P.; Gao, F. Generating daily land surface temperature at Landsat resolution by fusing Landsat and MODIS data. Remote Sens. Environ. 2014, 145, 55–67. [Google Scholar] [CrossRef]
- Mitraka, Z.; Chrysoulakis, N. Advanced Satellite Image fusIon Techniques for Estimating High Resolution Land Surface Temperature Time Series. In Proceedings of the 12th International Conference on Meteorology, Climatology and Atmospheric Physics (COMECAP), Heraklion, Greece, 28–31 May 2014; Volume 2, pp. 267–271. [Google Scholar]
- Mitraka, Z.; Chrysoulakis, N.; Doxani, G.; Del Frate, F.; Berger, M. Urban surface temperature time series estimation at the local scale by spatial-spectral unmixing of satellite observations. Remote Sens. 2015, 7, 4139–4156. [Google Scholar] [CrossRef]
- Voogt, J.A.; Grimmond, C. Modeling surface sensible heat flux using surface radiative temperatures in a simple urban area. J. Appl. Meteorol. 2000, 39, 1679–1699. [Google Scholar] [CrossRef]
- Gillies, R.R.; Carlson, T.N. Thermal remote sensing of surface soil water content with partial vegetation cover for incorporation into climate models. J. Appl. Meteorol. 1995, 34, 745–756. [Google Scholar] [CrossRef]
- McVicar, T.R.; Jupp, D. Using covariates to spatially interpolate moisture availability in the Murray-Darling basin: A novel use of remotely sensed data. Remote Sens. Environ. 2002, 79, 199–212. [Google Scholar] [CrossRef]
- Good, E.J. An in situ-based analysis of the relationship between land surface “skin” and screen-level air temperatures. J. Geophys. Res. 2016, 121, 8801–8819. [Google Scholar] [CrossRef]
- Rozenstein, O.; Qin, Z.; Derimian, Y.; Karnieli, A. Derivation of land surface temperature for Landsat-8 TIRS using a split window algorithm. Sensors 2014, 14, 5768–5780. [Google Scholar] [CrossRef] [PubMed]
- Barsi, J.; Schott, J.; Hook, S.; Raqueno, N.; Markham, B.; Radocinski, R. Landsat-8 thermal infrared sensor (TIRS) vicarious radiometric calibration. Remote Sens. 2014, 6, 11607–11626. [Google Scholar] [CrossRef]
- Montanaro, M.; Gerace, A.; Lunsford, A.; Reuter, D. Stray light artifacts in imagery from the Landsat 8 thermal infrared sensor. Remote Sens. 2014, 6, 10435–10456. [Google Scholar] [CrossRef]
- Gerace, A.; Montanaro, M. Derivation and validation of the stray light correction algorithm for the thermal infrared sensor onboard Landsat 8. Remote Sens. Environ. 2017, 191, 246–257. [Google Scholar] [CrossRef]
- Barsi, J. TIRS Stray Light Correction Update. Available online: https://atmcorr.gsfc.nasa.gov/tirs_notice.html (accessed on 23 May 2017).
- Abreu, L.; Anderson, G. The MODTRAN 2/3 report and LOWTRAN 7 model. Contract 1996, 19628, 132. [Google Scholar]
- Kneizys, F.; Abreu, L.; Anderson, G.; Chetwynd, J.; Shettle, E.; Berk, A.; Bernstein, L.; Robertson, D.; Acharya, P.; Rothman, L. The MODTRAN 2/3 Report and LOWTRAN 7 Model; Phillips Laboratory: Hanscom AFB, MA, USA, 1996. [Google Scholar]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.J.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Hoke, M.L.; et al. MODTRAN 5: A Reformulated Atmospheric Band Model with Auxiliary Species and Practical Multiple Scattering Options. In Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI; Shen, S.S., Lewis, P.E., Eds.; SPIE: Orlando, FL, USA, 2005; pp. 341–347. [Google Scholar]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. MODTRAN: A Moderate Resolution Model for LOWTRAN; DTIC Document; Spectral Sciences Inc.: Burlington, MA, USA, 1987. [Google Scholar]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Kistler, R.; Collins, W.; Saha, S.; White, G.; Woollen, J.; Kalnay, E.; Chelliah, M.; Ebisuzaki, W.; Kanamitsu, M.; Kousky, V.; et al. The NCEP-NCAR 50-year reanalysis. Bull. Am. Meteorol. Soc. 2001, 82, 247–267. [Google Scholar] [CrossRef]
- Barsi, J.; Barker, J.; Schott, J. An Atmospheric Correction Parameter Calculator for a Single Thermal Band Earth-Sensing Instrument. In Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 3014–3016. [Google Scholar]
- Barsi, J.; Schott, J.; Palluconi, F.; Hook, S. Validation of a web-based atmospheric correction tool for single thermal band instruments. In Proceedings of the SPIE 5882, Earth Observing Systems X, San Diego, CA, USA, 7 September 2005; p. 7. [Google Scholar]
- Foody, G.M.; Lucas, R.M.; Curran, P.J.; Honzak, M. Non-linear mixture modelling without end-members using an artificial neural network. Int. J. Remote Sens. 1997, 18, 937–953. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. Estimating very high resolution urban surface temperature using a spectral unmixing and thermal mixing approach. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 155–164. [Google Scholar] [CrossRef]
- Deng, C.; Wu, C. Examining the impacts of urban biophysical compositions on surface urban heat island: A spectral unmixing and thermal mixing approach. Remote Sens. Environ. 2013, 131, 262–274. [Google Scholar] [CrossRef]
- Cheng, K.-S.; Su, Y.-F.; Kuo, F.-T.; Hung, W.-C.; Chiang, J.-L. Assessing the effect of landcover changes on air temperature using remote sensing images—A pilot study in northern Taiwan. Landsc. Urban Plan. 2008, 85, 85–96. [Google Scholar] [CrossRef]
- Freitas, S.C.; Trigo, I.F.; Macedo, J.; Barroso, C.; Silva, R.; Perdigão, R. Land surface temperature from multiple geostationary satellites. Int. J. Remote Sens. 2013, 34, 3051–3068. [Google Scholar] [CrossRef]
- Schmutz, M.; Vogt, R.; Feigenwinter, C.; Parlow, E. Ten years of eddy covariance measurements in Basel, Switzerland: Seasonal and interannual variabilities of urban CO2 mole fraction and flux. J. Geophys. Res. 2016, 121, 8649–8667. [Google Scholar] [CrossRef]
- Wicki, A.; Parlow, E. Attribution of local climate zones using a multitemporal land use/land cover classification scheme. J. Appl. Remote Sens. 2017, 11, 026001. [Google Scholar] [CrossRef]
- Basel-Stadt. Geoportal Kanton Basel-Stadt; Grundbuch- und Vermessungsamt des Kantons Basel-Stadt: Basel-Stadt, Switzerland, 2016.
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- MeteoSwiss. Climate Normals Basel/Binningen; Reference Period 1981−2010; Federal Office of Meteorology and Climatology MeteoSwiss: Zurich, Switzerland, 2016. [Google Scholar]
- Basel-Stadt. Basel-Stadt in Zahlen 2015; Statistisches Amt des Kantons Basel-Stadt: Basel, Switzerland, 2015. [Google Scholar]
- Coll, C.; Galve, J.M.; Sanchez, J.M.; Caselles, V. Validation of Landsat-7/ETM+ thermal-band calibration and atmospheric correction with ground-based measurements. IEEE Trans. Geosci. Remote Sens. 2010, 48, 547–555. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martìnez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote Sens. 2008, 46, 316–327. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the Great Plains with ERTS. NASA: Washington, DC, USA,, 1974. [Google Scholar]
- Goward, S.N.; Markham, B.; Dye, D.G.; Dulaney, W.; Yang, J. Normalized difference vegetation index measurements from the Advanced Very High Resolution Radiometer. Remote Sens. Environ. 1991, 35, 257–277. [Google Scholar] [CrossRef]
- Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Wentz, E.; Anderson, S.; Fragkias, M.; Netzband, M.; Mesev, V.; Myint, S.; Quattrochi, D.; Rahman, A.; Seto, K. Supporting global environmental change research: A review of trends and knowledge gaps in urban remote sensing. Remote Sens. 2014, 6, 3879–3905. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Varshney, A. Improved NDBI differencing algorithm for built-up regions change detection from remote-sensing data: An automated approach. Remote Sens. Lett. 2013, 4, 504–512. [Google Scholar] [CrossRef]
- Xu, H. Extraction of urban built-up land features from Landsat imagery using a thematic oriented index combination technique. Photogramm. Eng. Remote Sens. 2007, 73, 1381–1391. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Gillespie, A.; Sabol, D.; Gustafson, W.T. Improved land surface emissivities over agricultural areas using ASTER NDVI. Remote Sens. Environ. 2006, 103, 474–487. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens. 2000, 21, 353–366. [Google Scholar] [CrossRef]
- Baldridge, A.M.; Hook, S.J.; Grove, C.I.; Rivera, G. The ASTER spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Paolini, L. Land surface temperature retrieval from Landsat 5 TM. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Barsi, J.A.; Schott, J.R.; Palluconi, F.D.; Hook, S.J. Validation of a Web-Based Atmospheric Correction Tool for Single Thermal Band Instruments. In Optics & Photonics 2005; SPIE: San Diego, CA, USA, 2005. [Google Scholar]
- Liang, S. Narrowband to broadband conversions of land surface albedo I. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Parlow, E. Correction of Terrain Controlled Illumination Effects in Satellite Data. In Progress in Environmental Research and Applications; Parlow, E., Ed.; Balkema: Rotterdam, The Netherlands, 1996; pp. 139–145. [Google Scholar]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. Error sources on the land surface temperature retrieved from thermal infrared single channel remote sensing data. Int. J. Remote Sens. 2006, 27, 999–1014. [Google Scholar] [CrossRef]
- Rigo, G.; Parlow, E. Modelling the ground heat flux of an urban area using remote sensing data. Theor. Appl. Climatol. 2007, 90, 185–199. [Google Scholar] [CrossRef]
- Christen, A.; Vogt, R. Energy and radiation balance of a central European city. Int. J. Climatol. 2004, 24, 1395–1421. [Google Scholar] [CrossRef]
- Canouï-Poitrine, F.; Cadot, E.; Spira, A.; Spira, A. Excess deaths during the August 2003 heat wave in Paris, France. Revue D’Épidémiol. Santé Publique 2006, 54, 127–135. [Google Scholar] [CrossRef]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an urban area: A case study for Hamburg, Germany. Remote Sens. 2012, 4, 3184–3200. [Google Scholar] [CrossRef]
- Su, Y.-F.; Foody, G.M.; Cheng, K.-S. Spatial non-stationarity in the relationships between land cover and surface temperature in an urban heat island and its impacts on thermally sensitive populations. Landsc. Urban Plan. 2012, 107, 172–180. [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, Y. Analysis of urban heat-island effect using ASTER and ETM+ data: Separation of anthropogenic heat discharge and natural heat radiation from sensible heat flux. Remote Sens. Environ. 2005, 99, 44–54. [Google Scholar] [CrossRef]
- Kato, S.; Yamaguchi, Y. Estimation of storage heat flux in an urban area using ASTER data. Remote Sens. Environ. 2007, 110, 1–17. [Google Scholar] [CrossRef]
- Anandakumar, K. A study on the partition of net radiation into heat fluxes on a dry asphalt surface. Atmos. Environ. 1999, 33, 3911–3918. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Esch, T.; Grimmond, C.S.B.; Parlow, E.; Lindberg, F.; Frate, D.; Feigenwinter, C. A novel approach for anthropogenic heat flux estimation from space. In Proceedings of the 9th International Conference on Urban Climate (ICUC9), Toulouse, France, 20–24 July 2015. [Google Scholar]









| Type | Dataset | Acquisition Date/Last Update |
|---|---|---|
| Raster | Landsat 8 OLI/TIR Path 195/Row 27 | 5 June 2013, 20 March 2014, 8 June 2014, 14 October 2014, 8 April 2015, 24 April 2015, 11 June 2015, 30 August 2015, 1 October 2015, 2 November 2015, 20 December 2015, 10 April 2016, 16 August 2016, 20 November 2016, 28 March 2017 |
| Landsat 8 OLI/TIR Path 196/Row 27 | 25 April 2013, 14 July 2013, 15 August 2013, 17 July 2014, 2 October 2015, 26 February 2015, 14 March 2015, 15 April 2015, 4 July 2015, 5 August 2015, 21 August 2015, 27 December 2015, 7 August 2016, 23 August 2016, 8 September 2016, 24 September 2016, 15 February 2017 | |
| LULC map | Created September 2015 using data from 2013–2015 [64] | |
| ASTER GDEM | June 2009 | |
| Vector | Residential units | 26 February 2014 |
| Meteo | Temperature, relative humidity and air pressure | March 2013 to March 2017 at MCR University Basel measurement tower [63] |
| NCEP reanalysis data | Data access from August 2015 to April 2017 [54,55,56] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wicki, A.; Parlow, E. Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment. Remote Sens. 2017, 9, 684. https://doi.org/10.3390/rs9070684
Wicki A, Parlow E. Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment. Remote Sensing. 2017; 9(7):684. https://doi.org/10.3390/rs9070684
Chicago/Turabian StyleWicki, Andreas, and Eberhard Parlow. 2017. "Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment" Remote Sensing 9, no. 7: 684. https://doi.org/10.3390/rs9070684
APA StyleWicki, A., & Parlow, E. (2017). Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment. Remote Sensing, 9(7), 684. https://doi.org/10.3390/rs9070684