Considering Inter-Frequency Clock Bias for BDS Triple-Frequency Precise Point Positioning

Abstract

The joint use of multi-frequency signals brings new prospects for precise positioning and has become a trend in Global Navigation Satellite System (GNSS) development. However, a new type of inter-frequency clock bias (IFCB), namely the difference between satellite clocks computed with different ionospheric-free carrier phase combinations, was noticed. Consequently, the B1/B3 precise point positioning (PPP) cannot directly use the current B1/B2 clock products. Datasets from 35 globally distributed stations are employed to investigate the IFCB. For new generation BeiDou Navigation Satellite System (BDS) satellites, namely BDS-3 satellites, the IFCB between B1/B2a and B1/B3 satellite clocks, between B1/B2b and B1/B3 satellite clocks, between B1C/B2a and B1C/B3 satellite clocks, and between B1C/B2b and B1C/B3 satellite clocks is analyzed, and no significant IFCB variations can be observed. The IFCB between B1/B2 and B1/B3 satellite clocks for BDS-2 satellites varies with time, and the IFCB variations are generally confined to peak amplitudes of about 5 cm. The IFCB of BDS-2 satellites exhibits periodic signal, and the accuracy of prediction for IFCB, namely the root mean square (RMS) statistic of the difference between predicted and estimated IFCB values, is 1.2 cm. A triple-frequency PPP model with consideration of IFCB is developed. Compared with B1/B2-based PPP, the positioning accuracy of triple-frequency PPP with BDS-2 satellites can be improved by 12%, 25% and 10% in east, north and vertical directions, respectively.

1. Introduction

In a quest for independence, China has pursued the build-up of a proprietary national navigation satellite system for many years. According to the deployment timeline of the BeiDou navigation satellite system (BDS), its implementation has been carried out in three steps: BeiDou navigation demonstration system by 2000, regional BDS (BDS-2) by 2012 and global BDS (BDS-3) by 2020. So far, the first two steps have been realized. The deployment and operation of the demonstration system was successful. With the successful launch of the first BDS-2 satellite M1 into the Medium Earth Orbit (MEO) in 2007, the BDS-2 was initiated. A preliminary start of navigation and position services was declared on 27 December 2011. Along with the launch of the last Geostationary Earth Orbit (GEO) satellite G6 on 25 October 2012, the BDS-2 was successfully established. The official declaration of navigation and position services covering the Asia-Pacific region was made on 27 December 2012 with a BDS-2 constellation of 14 operational satellites. In 2015, China started to build up the BDS-3. So far, 5 BDS-3 In-Orbit Validation (IOV) satellites have been launched, which marks the BDS expansion from the regional to global scale. The fully deployed BDS-3 constellation will consist of 5 GEO satellites, 27 MEO satellites and 3 Inclined Geosynchronous Orbit (IGSO) satellites [1].

The Chinese BDS, the European Galileo system, the Japanese Quasi-Zenith Satellite System (QZSS), the Global Positioning System (GPS) Block IIF satellites, the GLONASS-K satellites and partial GLONASS-M satellites provide signals on three or more frequencies. The available triple-frequency signals open new prospects for integrity monitoring [2], for fast ambiguity resolution (AR) in precise relative positioning [3], for precise point positioning (PPP) [4,5] and for ionospheric refraction analysis [6]. With the availability of more satellites from GLONASS, BDS and Galileo, many researchers focus on multi-constellation integration [7,8,9,10,11,12]. The newly emerging situation is that the integration of multi-frequency signals has also become a trend in Global Navigation Satellite System (GNSS) development.

In spite of the benefits from triple-frequency integration, an apparent inconsistency of up to 10 cm between the L1, L2 and L5 carriers was identified [13]. The L1/L2/L5 inconsistency, termed inter-frequency clock bias (IFCB), was defined as the difference between the precise satellite clock products calculated by two different ionospheric-free linear combinations of L1/L2 and L1/L5 carrier phase observations, and most likely attributed to the temperature-dependent and frequency-dependent phase bias [14]. On the contrary, the QZSS exhibited a good L1/L2/L5 consistency and no significant bias variations were observed [15,16]. For Galileo, full consistency of three carriers could also be ensured [17]. There were small bias variations with respect to B1, B2 and B3 carriers for BDS-2 satellites, but the relevant IFCB variations were generally confined to the amplitude limits of about 2 cm [18,19]. Since the amplitudes of single-day IFCB time series vary with time [20], their results, which were obtained based on a fairly limited amount of data, need to be further validated. The BDS-3 satellites transmit several new navigation signals, which provide more choices to form the ionospheric-free linear combination utilized for PPP. A further characterization and understanding of IFCB for BDS-2 and BDS-3 satellites is required. In addition, most of scientific studies on IFCB have focused on its characteristics and modeling, but rarely involve its effects on position determination. Actually, the high-precision IFCB estimates enable the consistent use of B1/B2 satellite clock products in B1/B3-based precise positioning.

The main work includes the analysis of IFCB characteristics for BDS-2 and BDS-3 satellites and IFCB effects on BDS triple-frequency PPP. The contribution starts with the description of materials and methods, including the estimation approach for IFCB and the development of triple-frequency PPP model with consideration of IFCB. Subsequently, we show and analyze our results in terms of space segment and navigation signals, data acquisition, characteristics of IFCB and performance evaluation of triple-frequency PPP. Finally, we summarize the main points and conclusions.

2. Materials and Methods

2.1. Estimation of Inter-Frequency Clock Bias

The carrier phase measurements L_k (k = 1, 2, 3) collected on the B1, B2 and B3 frequencies may be described as follows:

$$L_k=\rho +c\mathrm{d}{t}_r+(-c\mathrm{d}t+b_k)+T-I_1\cdot f_1^2/f_k^2+N_k$$

(1)

where ρ is the geometric range, cdt_r is the receiver clock offset, cdt is the satellite clock offset included in a parenthesis, b_k is the satellite-, signal- and time-dependent phase bias and the parenthesis shows a combination of b_k and cdt, T is the tropospheric delay, f is the carrier phase frequency, I₁ is the ionospheric delay on B1 frequency, and N is the phase ambiguity term grouped with the stable receiver-dependent phase hardware delay as well as the constant portion of the satellite phase hardware delay. According to Pan et al. [20], the time-varying portion of phase hardware delay at the satellite may result in the phase bias b_k.

In the BDS satellite orbit and clock determination, the B1/B2 ionospheric-free combined carrier phase observations are used. The satellite clock offset estimate can be shown below:

$$c{\overline{\mathrm{d}t}}_{12}=c\mathrm{d}t-(\frac{f_1^2}{f_1^2-f_2^2}\cdot b_1-\frac{f_2^2}{f_1^2-f_2^2}\cdot b_2)$$

(2)

where cdt₁₂ is the satellite clock offset estimate using B1/B2 observations.

As can be seen from Equation (2), the satellite clock offset estimate is different from the corresponding true value and there is an extra linear combination term of phase biases on B1 and B2 frequencies. The satellite clock offset estimated with B1/B3 observations may be different from the estimate using legacy B1/B2 measurements because of the presence of frequency-dependent phase bias b_k. From Equations (1) and (2), we can recognize that the difference between two ionospheric-free combinations of B1/B2 and B1/B3 carrier phase observations equals the sum of the difference between B1/B3 and B1/B2 satellite clock estimates and an additional ambiguity term. The ambiguity term is constant over each continuous ambiguity block. The differenced ionospheric-free (DIF) measurements, namely the triple-frequency carrier phase combination, can be expressed as:

$$DIF(L_1,L_2,L_3)=IF(L_1,L_2)-IF(L_1,L_3)=c{\overline{\mathrm{d}t}}_{13}-c{\overline{\mathrm{d}t}}_{12}+N_{DIF}$$

(3)

where N_DIF is the phase ambiguity of DIF measurement.

Rewriting Equation (3), the following equation can be obtained:

$$\delta =c{\overline{\mathrm{d}t}}_{13}-c{\overline{\mathrm{d}t}}_{12}=DIF(L_1,L_2,L_3)-N_{DIF}$$

(4)

where δ is the inter-frequency clock bias. Based on Equation (4), the IFCB is directly observable from DIF measurements. It is assumed that the similar phase errors, which are frequency dependent and change over time, do not exist in the receiver. For the purpose of fast IFCB estimation, we adopt the epoch-differenced (ED) strategy in this study [21]. As the IFCB is both satellite dependent and station independent, the ED strategy is feasible [20]. Since the phase ambiguity term in Equation (4) is invariable when the carrier phase observations on B1, B2 and B3 frequencies are free of cycle slips, it can be eliminated by between-epoch single-difference. The difference between B2 and B3 frequencies roughly equals to one-twentieth of their specific frequency values. Considering that the B2 and B3 frequencies are quite close, the phase center variations and phase wind-up effects are almost removed from DIF measurements. The ED IFCB at station r for satellite s between two adjacent epochs t and t−1 can be calculated as:

$$\mathsf{\Delta }{\delta }_r^s(t,t-1)=DIF{(L_1,L_2,L_3)}_r^s(t)-DIF{(L_1,L_2,L_3)}_r^s(t-1)$$

(5)

where Δδ is the ED IFCB.

A weighted average processing is conducted to achieve more reliable and accurate ED IFCB estimates. Assuming that the satellite s at epochs t and t−1 is successfully tracked for n stations in the network, the final ED IFCB estimate between the two epochs for satellite s can be depicted as:

$$\mathsf{\Delta }{\delta }^s(t,t-1)=\left({\displaystyle \sum _{r=1}^n\mathsf{\Delta }{\delta }_r^s(t,t-1)\cdot w_r^s(t,t-1)}\right)/\left({\displaystyle \sum _{r=1}^n{w}_r^s(t,t-1)}\right)$$

(6)

$$w_r^s(t,t-1)=\{\begin{array}{cc}\sin E_r^s(t,t-1)& E_r^s(t,t-1)<40°\\ 1& E_r^s(t,t-1)\ge 40°\end{array}$$

(7)

where $E_r^s$(t, t−1) is the average satellite elevation angle over the epochs t and t−1 at station r for satellite s, and w is the weight, which is elevation dependent and decomposed into a sinusoidal function and a constant function over different elevation ranges. In general, the measurement noises on a single frequency increase as the satellite elevation angles decrease [17]. Considering the linear combination, similar discussions on measurement noises can be found in the literatures [22,23,24]. Therefore, the ED IFCB solutions at the station with lower elevation angles are down-weighted. After comprehensively considering the accuracy and reliability of ED IFCB estimates, an empirical determination of 40° for elevation threshold is adopted.

Multipath is a significant and largely unmodeled source for satellite positioning errors. The BDS or GPS multipath can be extracted using the ionospheric-free geometric linear combination, and the ionospheric-free combination as well as multipath signals mostly varies due to variability of satellite elevation angles and receiver’s antenna height [25]. According to Najibi and Jin [26], the multipath signals are more sensitive to the satellite elevation angle variations than the receiver’s antenna height changes. The ED IFCB estimates derived from DIF measurements, which consist of two different ionospheric-free carrier phase combinations, will suffer from multipath effects. Since the physical surface formation surrounding the ground station receivers used in this paper does not change during a certain time span, the impact of variability of receiver’s antenna height should not be considered. Bilich et al. [27] illustrated the elevation angle dependence of phase multipath error. The satellite signals with low elevation angles exhibit large multipath, especially for those below 35° elevation. Therefore, the elevation-dependent weighting shown in Equation (7) can significantly weaken the effects of multipath.

The IFCB can be obtained through an accumulation of ED IFCB estimates. In addition, a reference epoch with an assumption of IFCB value should be selected. The IFCB for satellite s at epoch t can be written as:

$${\delta }^s(t)={\delta }^s(t_0)+{\displaystyle \sum _{p=t_0+1}^t\mathsf{\Delta }{\delta }^s(p,p-1)}$$

(8)

where δ^s(t₀) is the IFCB for satellite s at the reference epoch t₀, and Δδ^s(p, p−1) is the ED IFCB for satellite s between the adjacent epochs p and p−1. The IFCB value at the epoch 00:00:00 (GPS time) is set to zero for each day, and this epoch is selected as the reference epoch in this study. The IFCB estimates at all epochs of a day will contain a common bias. In parameter estimation process, the common bias will be absorbed by the phase ambiguity term, and thus has no effect on PPP float solutions. Since the phase bias b_k is station independent, it is eliminated in between-receiver single-difference. Therefore, the triple-frequency signals can be directly used in precise relative positioning and the issue of IFCB is absent. As the PPP usually adopts undifferenced model, the phase bias b_k cannot be eliminated by between-receiver single-difference. In addition, phase bias b_k is time-varying and satellite-dependent, and cannot be absorbed by phase ambiguity or receiver clock parameters. Thus, the issue of IFCB should be carefully handled when the triple-frequency signals are simultaneously used in PPP.

2.2. Triple-Frequency Precise Point Positioning Model

Actually, the IFCB estimate obtained from the above IFCB estimation process is a linear combination of the phase biases on B1, B2 and B3 frequencies, and thus it is termed phase-specific IFCB. In addition to the phase-specific IFCB, the whole IFCB estimate should also contain the code-specific IFCB, which is a linear combination of the constant code hardware biases on B1, B2 and B3 frequencies. The code-specific IFCB can be computed through the triple-frequency code observations, and it can also be expressed as a function of differential code biases (DCBs) [21]. A new type of elevation- and frequency-dependent systematic bias, termed satellite-induced code bias (SICB), was identified to exist in the code observations from BDS-2 satellites [28]. The SICB is ignored during the generation process of DCB products. Therefore, the SICB will affect the estimation of code-specific IFCB when using either triple-frequency code observations or DCBs. Although some literatures, such as [21], claimed that the code-specific IFCB is stable, its stability needs further investigation as the phase-specific IFCB shows variations of several centimeters during a day. The stability of code-specific IFCB will also affect its estimation. For completeness, the results of triple-frequency PPP using L₁/L₂ and L₁/L₃ phase observations as well as P₁/P₂ and P₁/P₃ code observations are also presented in the next section. The code-specific IFCB is simply calculated using the DCB products. Compared to the results of triple-frequency PPP ignoring P₁/P₃ code observations, the convergence time is reduced by 1.1−3.6 min, but their positioning accuracy is found to be at the same level. It is indicated that the positive role that the code observations could play in the improvement for PPP on positioning accuracy and convergence time is limited at present. Despite this, greater benefits from P₁/P₃ code observations for triple-frequency PPP can be expected after carefully handling the above issues on code-specific IFCB. In the future, we will thoroughly analyze the code-specific IFCB, including the mitigation of SICB, the effect of SICB on its estimation, the stability, the effect of stability on its estimation, and its effect on triple-frequency PPP. After this, the P₁/P₃ code observations and code-specific IFCB corrections will be included in the triple-frequency PPP model. In this paper, we mainly focus on the phase-specific IFCB. In the triple-frequency PPP model developed here, only the ionospheric-free linear combination of P₁/P₂ code observations is applied and the P₁/P₃ ionospheric-free combined code observations are not used. P_k (k = 1, 2, 3) is the measured pseudorange on B1, B2 and B3 frequencies.

The first-order ionospheric delay errors are removed by utilizing ionospheric-free combined observables. The triple-frequency PPP observation model with consideration of IFCB may be given as follows:

$$IF(P_1,P_2)=\rho +c{\overline{\mathrm{d}t}}_r-c{\overline{\mathrm{d}t}}_{12}+T$$

(9)

$$IF(L_1,L_2)=\rho +c{\overline{\mathrm{d}t}}_r-c{\overline{\mathrm{d}t}}_{12}+T+{\overline{N}}_{12}$$

(10)

$$IF(L_1,L_3)=\rho +c{\overline{\mathrm{d}t}}_r-c{\overline{\mathrm{d}t}}_{13}+T+{\overline{N}}_{13}$$

(11)

$$c{\overline{\mathrm{d}t}}_{13}=c{\overline{\mathrm{d}t}}_{12}+\delta$$

(12)

where cdt₁₂ is the precise satellite clock corrections generated and released by Multi-GNSS Experiment (MGEX), cdt_r is the receiver clock offset grouped with code hardware bias at the receiver, and N is the phase ambiguity term that has been grouped with the receiver-dependent uncalibrated phase delay (UPD) and code hardware bias as well as the corresponding satellite-specific ones. The unknown parameters including three-dimensional (3D) coordinates, tropospheric zenith wet delay (ZWD), receiver clock offset and real-valued B1/B2 and B1/B3 phase ambiguity parameters need to be estimated. The number of ambiguity parameters is twice as large as the BDS satellite number.

Appropriate stochastic models should be provided for the measurements in the Kalman filter [29] applied to BDS triple-frequency PPP. For either code or carrier phase, the ionospheric-free combined observations are a linear combination of original measurements on two different frequencies. Assuming there is no correlation between the measurements on different frequencies, of different types or from different satellites, the covariance matrix of observations for a BDS satellite is obtained by the law of random error propagation as given below:

$$Q=\left[\begin{array}{ccc}(a_{12,1}^2+a_{12,2}^2)\cdot {\sigma }_P^2& 0& 0\\ 0& (a_{12,1}^2+a_{12,2}^2)\cdot {\sigma }_L^2& (a_{12,1}\cdot a_{13,1})\cdot {\sigma }_L^2\\ 0& (a_{12,1}\cdot a_{13,1})\cdot {\sigma }_L^2& (a_{13,1}^2+a_{13,2}^2)\cdot {\sigma }_L^2\end{array}\right]$$

(13)

with $a_{12,1}=f_1^2/(f_1^2-f_2^2),$ $a_{12,2}=f_2^2/(f_1^2-f_2^2),$ $a_{13,1}=f_1^2/(f_1^2-f_3^2),$ and $a_{13,2}=f_3^2/(f_1^2-f_3^2)$ where ${\sigma }_P^2$ is the variance of code observations, and ${\sigma }_L^2$ is the variance of carrier phase observations. Regarding the actual variance, it is defined as a function of the satellite elevation angle and initial variance [30].

The file “igs08_wwww.atx” provided by International GNSS Service (IGS) is adopted to correct the phase center offsets (PCOs) of satellite antenna for BDS on B1, B2 and B3 frequencies. Currently, the BDS satellite phase center variations (PCVs) on the three frequencies are still unavailable. In order to keep consistency with the strategies adopted in the BDS precise satellite orbit determination and clock estimation, the PCO and PCV corrections of receiver antenna on GPS L1 and L2 frequencies are simply used for BDS B1 and B2 signals, respectively [8]. In view that there is only a small difference between GPS L2 and BDS B3 frequencies, we simply use the PCO and PCV corrections of receiver antenna on L2 frequency for B3 frequency. The data processing models and strategies for BDS triple-frequency PPP are summarized in

Table 1. Data processing models and strategies for BDS triple-frequency PPP.

Item	Models and Strategies	Spectral Density and Precision
Observations	Undifferenced code and carrier phase observations	Code observations: 0.6 m Phase observations: 0.004 m
Signal selection	B1/B2 and B1/B3	-
Observation weighting	Elevation-dependent weight	-
Elevation mask angle	10°	-
Sampling interval	30 s	-
Satellite orbit	Fixed using the products from MGEX	-
Satellite clock	Fixed using the products from MGEX	-
Phase wind-up effect	Corrected	-
Earth rotation parameter	Fixed	-
Station displacement	Solid Earth tides, ocean tide loading, pole tides, IERS Convention 2003	-
Relativistic effect	IERS Convention 2003	-
Phase center offset	Satellite: corrected using IGS values	-
	Receiver: corrected using GPS values from IGS
Phase center variation	Satellite: neglected; Receiver: corrected using GPS values from IGS	-
Ionospheric delay	First-order effect eliminated by ionospheric-free linear combination	-
Tropospheric delay	Dry part: corrected using Saastamoinen tropospheric model	Tropospheric ZWD: 10−9 m2/s
	Wet part: estimated; Mapping functions: GMF [33]
	Tropospheric ZWD: modeled as a random walk (RW) process
Receiver coordinate	Static: estimated and modeled as constants	Kinematic: 102 m2/s
	Kinematic: estimated and modeled as a RW process
Receiver clock	Estimated and modeled as a RW process	105 m2/s
Phase ambiguity	Estimated and modeled as constants	-
Terrestrial frame	ITRF2008	-
Time system	GPS Time	-

. In addition, Table 1 also details the specific implementation of dynamic models for state vector and stochastic models for measurements [9]. The code and phase observation precision for GPS are usually set to 0.3 and 0.002 m, respectively [31,32]. Compared with GPS, BDS satellite orbit and clock are at a relatively lower accuracy and BDS measurements exhibit relatively higher noise level [9,17]. Therefore, the code and phase observation precision for BDS are empirically set to 0.6 and 0.004 m, respectively. Cai et al. [9] adopted same values for the precision of BDS observations. The stochastic model of measurements for BDS triple-frequency PPP needs further investigation.

3. Results

3.1. Space Segment and Navigation Signals

Up to 12 June 2016, 18 BDS-2 satellites and 5 BDS-3 satellites have been launched. Currently, three BDS-2 satellites, namely M1, G2 and M5, are no longer transmitting. In addition, the BDS-2 satellite G7 and BDS-3 satellite M3-S are in the phase of flight tests. As of October 2016, there are 14 BDS-2 satellites and 4 BDS-3 satellites in full operation, including 5 GEO, 8 IGSO and 5 MEO satellites. The information on the 18 operational satellites is included in

Table 2. BDS space segment as of October 2016.

Generation	Satellite	PRN	COSPAR ID	NORAD ID	Type	Orbit
BDS-2	G1	C01	2010-001A	36287	GEO	140.0°E
	G6	C02	2012-059A	38953	GEO	80°E
	G3	C03	2010-024A	36590	GEO	110.5°E
	G4	C04	2010-057A	37210	GEO	160.0°E
	G5	C05	2012-008A	38091	GEO	58.75°E
	I1	C06	2010-036A	36828	IGSO	~122°E
	I2	C07	2010-068A	37256	IGSO	~119°E
	I3	C08	2011-013A	37384	IGSO	~120°E
	I4	C09	2011-038A	37763	IGSO	~96.5°E
	I5	C10	2011-073A	37948	IGSO	~92.5°E
	M3	C11	2012-018A	38250	MEO	~21,528 km
	M4	C12	2012-018B	38251	MEO	~21,528 km
	M6	C14	2012-050B	38775	MEO	~21,528 km
	I6	C15/C13	2016-021A	41434	IGSO	~95°E
BDS-3	I1-S	C31	2015-019A	40549	IGSO	~93.5°E
	I2-S	C32	2015-053A	40938	IGSO	~96.5°E
	M1-S	C33	2015-037A	40748	MEO	~21,528 km
	M2-S	C34	2015-037B	40749	MEO	~21,528 km

. The GEO and IGSO satellites operate in orbit at an altitude of 35,786 km with a period of revolution of 23 h 56 min. The IGSO satellites have an inclination of 55°, while the GEO satellites exhibit a non-zero inclination of 0.7°–1.7°. The MEO satellites are in a nearly circular orbit at an altitude of 21,528 km and an inclination of 55°, and complete the orbit in approximately 12 h 53 min. A PRN switch from C15 to C13 for I6 spacecraft was carried out on 11 October 2016.

The 24-h ground tracks of BDS-2 and BDS-3 satellites available for positioning on 13 July 2016, are shown in Figure 1. The ground tracks of IGSO satellites describe two similar loops in the shape of figure-of-eight. The average difference between longitudes of the two loops is roughly 30°. For main-land China, IGSO satellites provide an optimum coverage. The satellites with inclined geosynchronous orbits show an improved availability in terms of high elevation angles. When users are in densely populated areas, the so-called “urban canyon” problem can be alleviated due to the presence of IGSO satellites. The ground tracks are confined from approximately 76.2°E to 138.0°E longitude and 57.5°S to 57.5°N latitude for the eight IGSO satellites. Five GEO satellites distributed in the Indian and Pacific oceans over the Equator further complement the IGSO constellation. As such, the users in Asian-Pacific regions can observe enough satellites. The five GEO satellites are fixed in longitude because of active control, whereas their ground tracks exhibit small variations of up to 2° in latitude. Similar to the GPS, GLONASS and Galileo satellites, the BDS MEO satellites offer complete global coverage. The ground tracks of the MEO satellites are confined from 56.1°S to 56.1°N latitude.

The BDS-2 satellites transmit navigation signals in QPSK modulation on a total of three frequency bands, namely B1, B2 and B3 [35]. Compared with the BDS-2 satellites, the signals of BDS-3 satellites are modified. In addition to B1 and B3 signals, the BDS-3 satellites are also capable of transmitting several new navigation signals, namely B1C, B2a and B2b. The B1C signal centered at 1,575.42 MHz is transmitted in TMBOC(6,1) modulation, and is compatible with GPS L1 signal and Galileo E1 signal. The B2a signal with a center frequency of 1176.45 MHz is modulated using BPSK(10), AltBOC(15,10) or TD-AltBOC(15,10) modulation, and is compatible with GPS L5 signal and Galileo E5a signal. The AltBOC(15,10) or TD-AltBOC(15,10) modulated B2b signal matches the Galileo E5b signal. It should be noted that the B2 signal of BDS-2 satellites and the B2b signal of BDS-3 satellites share the same frequency, but their modulation types are different. The carrier phase frequencies and chip rates of BDS signals covered by test receivers are provided in

Table 3. BDS signals.

Generation	Band	Frequency (MHz)	Chip Rate (Mcps)
BDS-2	B1	1561.098	2.046
	B2	1207.140	2.046
	B3	1268.520	10.23
BDS-3	B1	1561.098	2.046
	B1C	1575.420	1.023
	B2a	1176.450	10.23
	B2b	1207.140	10.23
	B3	1268.520	10.23

. The B1, B1C, B2a, B2b and B3 signals can be simultaneously tracked for the BDS-3 satellites I2-S, M1-S and M2-S, while the receiver can only track the B1 and B3 signals for the I1-S satellite.

3.2. Data Acquisition

In order to achieve a good coverage of different latitude and longitude areas, we select 35 stations. The geographical distribution of the selected stations is shown in Figure 2. The green points refer to MGEX stations, which can offer B1/B2/B3 BDS-2 tracking. The international GNSS Monitoring and Assessment System (iGMAS) stations, which are marked in blue and yellow in Figure 2, can track the B1, B2 and B3 signals of BDS-2 satellites. In addition, the yellow ones are also capable of tracking the B1 and B3 signals of BDS-3 satellites. The two stations marked in black, including the iGMAS station XIA1 and the station SGG1 operated at the School of Geodesy and Geomatics (SGG) of the Wuhan University in Wuhan, China, have the capability of tracking all the BDS signals listed in Table 3, except for the B2 signal for station XIA1. Observations from a 7-day interval from 7–13 July 2016 for station SGG1, a 14-day interval from 2–15 September 2016 for station XIA1 and a 32-day interval from 15 August–15 September 2016 for other stations are selected as the core datasets for this study.

3.3. Characteristics of IFCB

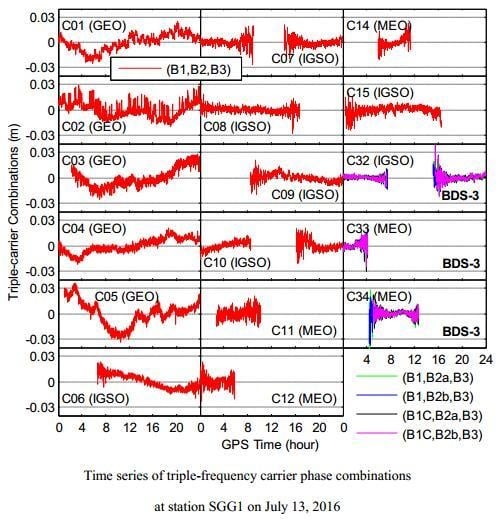
Figure 3 depicts the time series of B1/B2/B3 triple-carrier combinations for BDS-2 satellites as well as B1/B2a/B3, B1/B2b/B3, B1C/B2a/B3 and B1C/B2b/B3 triple-carrier combinations for BDS-3 satellites at station SGG1 on 13 July 2016. The triple-frequency carrier phase combination is actually the difference between two different ionospheric-free carrier phase combinations, and Equation (3) shows an example of B1/B2/B3 combination. Numerical values of the coefficients for each triple-frequency carrier phase combination are given in

Table 4. Coefficients for triple-frequency carrier phase combinations.

Combination	Coefficient
(B1, B2, B3)	(−0.457, −1.487, 1.944)
(B1, B2a, B3)	(−0.629, −1.314, 1.944)
(B1, B2b, B3)	(−0.457, −1.487, 1.944)
(B1C, B2a, B3)	(−0.583, −1.261, 1.844)
(B1C, B2b, B3)	(−0.422, −1.422, 1.844)

. The phase ambiguity in triple-frequency carrier phase combination shown in Equation (3) is determined as the mean value of triple-carrier combination time series over the common continuous ambiguity block for all B1, B2 and B3 carrier phase observations. The phase ambiguity estimate is then removed from the original triple-carrier combination time series. It seems that an alternative way can be used to estimate the IFCB. However, the satellite revisit time for the stations located in different areas is different. The different tracking time of a satellite will affect the magnitude of its IFCB estimates. Bias variations are most evident for the BDS-2 GEO satellites and the oldest spacecraft C06 among the IGSO satellites. As to other BDS-2 satellites, small bias variations can also be recognized but they are generally confined to less than 2 cm. For BDS-3 satellites, in contrast, no significant biased variations can be observed and changes of the triple-carrier combination are often dominated by receiver phase multipath and noise (PMN). After the ambiguity term is eliminated in Equation (3), the residuals mainly include a weighted sum of phase noise, multipath and hardware delay. According to Pan et al. [20], the receiver phase hardware delay should be stable over several hours, and thus it will be included in the phase ambiguity estimate and removed together with the ambiguity term. As to the satellite phase hardware delay, it will also be eliminated together with the ambiguity term since the triple-carrier combination time series of BDS-3 satellites do not show significant trend term. Therefore, the triple-carrier combination variations of BDS-3 satellites mainly show PMN changes. Similar discussions can also be found in Montenbruck et al. [18]. The above noise refers to the measurement noise in carrier phase observations.

The results shown in Figure 3 are obtained using a single station, which will be affected by numerous factors, such as the receiver quality, antenna quality and surrounding of the receiving antenna. Therefore, these results can only be roughly used for IFCB analysis. Actually, the triple-carrier combination time series show a comprehensive effect of the measurement noises, multipath as well as the time-varying portion of satellite phase hardware delay, namely IFCB. The satellite internal temperature variations due to varying sun illumination that depends on the relative geometry of the sun–spacecraft–earth may cause the variations of the satellite phase hardware delay, namely IFCB variations [14,20]. There is a negative correlation between the amplitude of single-day IFCB time series and the sun elevation above the satellite orbital plane. For the satellites with relatively lower sun elevation such as C05 and C06, the time series of triple-carrier combination show evident bias variations. As to BDS-3 satellites, there may be better thermal insulation processing at the signal transmission end. There are some reflectors near the station SGG1, including trees and walls. The multipath will have significant effect on the measurements for GEO satellites because of their almost constant elevation angles, especially for C05 with lowest elevation angles. The multipath is also an important attribution for the obvious bias variations of GEO satellites.

The root mean square (RMS) values of low-frequency and high-frequency components in the triple-frequency carrier phase combination time series for each BDS satellite are calculated using the datasets collected at SGG1 on 7–13 July 2016, and the results are shown in Figure 4. The wavelet decomposition and reconstruction is used to separate the low-frequency and high-frequency components from their combination. In this contribution, the threshold value for the distinction between low-frequency and high-frequency components is roughly 3 × 10⁻⁴ Hz, which is a compromise between different satellites since they show different noise level. It is important to note that the frequency threshold may be only appropriate for the datasets used in this paper. If we analyze the triple-carrier combination time series for GPS satellites, the frequency threshold should be determined once again. The Symlet wavelet ‘sym5’ is employed [36]. The high-frequency components mainly contain the PMN, while the low-frequency components mainly reflect the longer-term changes, namely IFCB variations. The RMS values of low-frequency components range from 0.2 to 0.9 mm for BDS-3 satellites, indicating that no significant IFCB variations can be observed for these satellites. The RMS values of low-frequency components vary within a range of 4.5–12.2 mm for BDS-2 GEO satellites, while the corresponding varying range is 0.8–5.2 and 0.7–0.9 mm for BDS-2 IGSO and MEO satellites, respectively. A further characterization and analysis of IFCB for BDS-2 satellites is required. It is interesting to note that the GEO satellites with relatively higher sun elevations above the satellite orbital plane such as C01 and C04 also have larger low-frequency components. This is because the low-frequency components may also contain partial multipath. Alternatively, other unknown factors may affect the variations of triple-frequency carrier phase combination with respect to a single station, which needs further investigation. Due to the comprehensive effects of multipath and IFCB, all the GEO satellites and the IGSO satellite C06 show larger RMS statistics of triple-carrier combination time series.

For the purpose of assessing the PMN level, the variation of RMS statistics of high-frequency components in the triple-carrier combination time series with elevation at SGG1 is plotted in Figure 5. The RMS values are computed with respect to the increment of satellite elevation angles in steps of 5°. The PMN variations are quite consistent for the four different triple-frequency carrier phase combinations of BDS-3 tracking. The BDS-2 satellites show larger carrier phase errors compared with BDS-3 satellites at mid and high elevation angles. At elevation angle of 87.5°, the RMS PMN for all four triple-carrier combinations of BDS-3 satellites is 0.8 mm, while the RMS PMN for the B1/B2/B3 triple-carrier combination of BDS-2 satellites is 1.7 mm. At the 22.5° elevation, the RMS PMN for the four different combinations of BDS-3 satellites varies in a range of 5.5–6.9 mm, while the corresponding RMS PMN for BDS-2 satellites is 3.5 mm. For comparison, the right plot illustrates the results from XIA1 of 2–15 September 2016. The receiver and antenna information for the stations SGG1 and XIA1 is listed in

Table 5. Information of two stations.

Station	Receiver Type	Receiver Number	Antenna Type	Antenna Number	Antenna Height
SGG1	prototype	-	TRM59900.00	-	0 m
	receiver		NONE
XIA1	gnss_ggr	RINTMR20160006	RINT-8CH	RINT-8CH-006	0.15 m

. A prototype receiver is set up at the station SGG1, and it is developed by one university in China. The stations SGG1 and XIA1 are equipped with different types of receivers and antennas. The comparison reveals the PMN differences caused by the different tracking performance of the specific receiver and antenna quality with respect to its multipath sensitivity as well as surrounding of the receiving antenna. According to the results at the two stations, the representative RMS errors at low elevations are 10 mm for the high-frequency components in the triple-frequency carrier phase combination, while the corresponding errors at medium and high elevations are 2 mm. Assuming, for simplicity, equal error variances on all frequencies, the 1σ PMN for triple-frequency combination is 2.3–2.5 times larger than that of the individual signals. We can conclude that the PMN errors for BDS tracking on a single frequency vary in a range of 1 to 4 mm over the considered satellite elevation ranges.

Based on ED strategy, the datasets on 32 consecutive days, i.e., 15 August–15 September 2016, are processed for all BDS-2 satellites. Figure 6 provides the time series of IFCB estimates. It is obvious that the IFCB changes over time, and the IFCB variations are generally confined to peak amplitudes of about 5 cm, except for C15. Most importantly, the IFCB exhibits notable periodic signal. The RMS statistics of IFCB estimates over the 32 days are also provided in each sub-figure. C01 has the smallest RMS values of 0.010 m, while C15 RMS values are the largest with value of 0.068 m. Compared with the results shown in Figure 3 and Figure 4, the results shown in Figure 6 can be better used for IFCB analysis. The IFCB estimation here is conducted based on a weighted average of solutions over the entire network, and thus the many influence factors such as measurement noises and multipath can be alleviated. Based on the law of random error propagation and reasonable assumption, the standard deviation (STD) of the IFCB estimates is computed and found to be usually smaller than 4 mm, except for C15. The sun elevation above the satellite orbital plane is highest for C01 during this period of time, and thus C01 has the smallest RMS IFCB. As to C06 and C08, they have the second largest RMS IFCB due to the relatively lower sun elevations. The reason for the largest RMS IFCB for C15 is that the number for stations with the capability of offering B1/B2/B3 tracking is not sufficient. The ED IFCB estimates for C15 are inaccurate at many epochs, and thus there are many accumulated errors when calculating the IFCB through accumulation. According to Pan et al. [20], the single-day IFCB time series of GPS show significant periods of 12, 8, 6, 4.8, 4 and 3 h. Some periods such as 8 h cannot be explained by the sun illumination, which indicates that other factors also affect the IFCB variations. Therefore, the factors that affect the IFCB variations need further investigation, but this does not limit the applications of IFCB to triple-frequency PPP.

The number of stations in the ground tracking network mainly determines the accuracy and reliability of IFCB estimates [21]. Taking into account the effect of measurement noises, it is better to use the sum of weights of ED IFCB for the reflection of the performance of IFCB estimates, as shown in Equation (6). Figure 7 shows the average values of sum of weights at an epoch over the 32 days for each BDS-2 satellite. It is observed that the average weight is only 3.1 for C15, while the average weight falls between 5.0 and 10.9 for other satellites. Due to the smaller weights, the IFCB estimates shown in Figure 6 exhibit higher noise level. The reason for the smallest weights from C15 is that many stations currently offer B1/B2 tracking rather than B1/B2/B3 tracking for this satellite. This explains the largest fluctuation amplitudes of IFCB time series for C15.

In real-time triple-frequency PPP, the IFCB should be estimated in real time. In addition to the computational burden, the data streams with BDS observations broadcast by a global ground tracking network should be received in real time. The above real-time estimation process for IFCB will bring additional heavy workload for the real-time triple-frequency PPP users. The IFCB prediction with a high accuracy is a possible way to minimize the workload. Following Pan et al. [20], the IFCB periods roughly coincide with the orbital repeat periods of the satellites. Thus, the IFCB of the first day is utilized to predict that of the second day for GEO and IGSO satellites and of the day after a week for MEO satellites. The similarity degree between single-day IFCB time series of two different days can be assessed by the cross-correlation [37]. A cross-correlation is performed on the single-day IFCB time series for two consecutive days or two days with an interval of a week. The normalized cross-correlation results at 1680 s lag for MEO satellites and at 240 s lag for GEO and IGSO satellites are shown in Figure 8. The time lag should be considered because of the difference between a solar day and a sidereal day. For all GEO and IGSO satellites except C01, C02 and C15, the cross-correlation values are larger than 0.6 for most cases. In addition, all MEO satellites show low similarity between waveforms of IFCB time series for two days, which may be attributed to the small IFCB variations and the long time span for IFCB prediction.

Table 6. Average cross-correlation values over 32 days for each BDS-2 satellite.

Orbit Type	Satellite PRN	Cross-Correlation
GEO	C01	0.512
	C02	0.292
	C03	0.678
	C04	0.816
	C05	0.828
IGSO	C06	0.893
	C07	0.592
	C08	0.617
	C09	0.786
	C10	0.745
	C15	0.501
MEO	C11	0.142
	C12	0.145
	C14	0.363

provides the average values of cross-correlation coefficient over 32 days for each BDS-2 satellite. According to the average results for the same orbit type of satellites, the cross-correlation coefficient between the IFCB series of two days is 0.625, 0.689 and 0.217 for GEO, IGSO and MEO satellites, respectively.

After subtracting IFCB time series of the first day from those of the day after a week for MEO satellites and of the second day for GEO and IGSO satellites, the residuals are plotted in Figure 9. The time lag is considered. The residual series show a decrease of fluctuation amplitudes from about 5 cm to about 3 cm in comparison to the IFCB series for most satellites. The RMS statistics of residuals for the 32 days are also shown in each panel. According to the average results of the 14 satellites, the prediction accuracy of IFCB is 1.2 cm.

3.4. Performance Evaluation of Triple-Frequency PPP

In order to validate the correctness of IFCB estimates, the performance of triple-frequency PPP is evaluated. The IFCB corrections are derived by prediction. As the precise satellite orbit and clock products of BDS-3 satellites are still unavailable, only BDS-2 satellites are used. For the purpose of comparison, the traditional B1/B2-based PPP processing is also carried out. The epoch-wise positioning errors for dual- and triple-frequency cases in the east, north and vertical directions at JFNG on 12 September 2016 are shown in Figure 10, and their variations are consistent for the two different cases in all three directions. Nevertheless, the convergence performance of triple-frequency case in the first two hours is slightly better than that of dual-frequency case. Compared to the dual-frequency PPP solutions, the triple-frequency PPP solutions are more stable even after a long convergence time. The RMS values of positioning errors over the last 15 min as well as the convergence time for dual- and triple-frequency PPP solutions are presented in

Table 7. Positioning accuracy and convergence time for three different cases at JFNG on 12 September 2016.

Item	Direction	B1/B2	B1/B2 + B1/B3 (with IFCB)	B1/B2 + B1/B3 (no IFCB)
Positioning Accuracy (cm)	East	1.2	0.8	1.4
	North	0.4	0.3	0.4
	Vertical	1.6	1.5	2.6
Convergence Time (min)	East	23.5	17.5	31
	North	7	5	15
	Vertical	132.5	130	134.5

. In this study, the position filter is considered to have converged when the positioning errors reach 0.1 m and keep within 0.1 m. According to Li et al. [38], the BDS B1/B2 PPP requires more than two hours to achieve a positioning accuracy better than 0.1 m for all three coordinate components. Therefore, our results are comparable to theirs. The reason for the longer convergence time of BDS PPP in comparison to GPS PPP is that the BDS satellite orbit and clock are at a relatively lower accuracy [9], and BDS measurements exhibit relatively higher noise level [17]. In addition, BDS position dilution of precision (PDOP) values are larger in most times than the GPS case although the former has more visible satellites at the station JFNG with the coverage of BDS service. For comparison, the epoch-wise positioning errors and the corresponding statistical values for the triple-frequency PPP without IFCB consideration are also shown in Figure 10 and Table 7. Its positioning accuracy and convergence performance are worse than those of the other two BDS PPP cases. The results indicate that the positioning performance will degrade without careful consideration of the IFCB, even if B1/B3 observations are added to the B1/B2 PPP processing.

The datasets from 9 stations covered by the BDS service of the Asia-Pacific area on 12–13 September 2016 are used for the accuracy statistics. For each 24-h session, the RMS statistics are computed using the positioning errors of the last 15 min. Theoretically, the position solution at the last epoch for the PPP with the use of Kalman filter has the highest positioning accuracy. However, the position solutions may still show fluctuations after a long observation time of approximately 24 hours if the re-convergence occurs due to the frequent cycle slips, the gross errors, the insufficient satellite number or even the signal blockage. For reliability, it may be better to use a period of time rather than an epoch at the end of a session for RMS calculation. Cai et al. [39] also adopted a time span of 15 min at the end of each session for RMS calculation. The average positioning errors for all 24-h cases are calculated based on the RMS values. An accuracy of 1.7, 0.4 and 2.0 cm in the east, north and vertical coordinate components is achieved for B1/B2 PPP, respectively. Taking IFCB into account, the triple-frequency PPP improves the positioning accuracy by 12%, 25% and 10% over the B1/B2 PPP to 1.5, 0.3 and 1.8 cm in the three coordinate components, respectively.

As there are mainly measurement noises as well as other unmodeled errors in observation residuals, they can be used for the evaluation of triple-frequency PPP model. The residuals of B1/B2 and B1/B3 ionospheric-free combined carrier phase observations in the triple-frequency PPP from JFNG of 12 September 2016 are shown in Figure 11. Different satellites are identified by different colors. The RMS values of phase residuals for all BDS-2 satellites are also given in each panel. B1/B2 and B1/B3 phase observation residuals appear at the same level and no significant systematic errors can be found in the B1/B3 phase residuals. It is suggested that we have properly handled the issue of satellite clocks in triple-frequency PPP model. For the purpose of further analysis, the B1/B3 phase observation residuals are re-computed when neglecting the IFCB, which indicates larger phase residuals with RMS statistics of 0.018 m. Although the difference between B1/B3 phase residuals of triple-frequency PPP with and without IFCB consideration is only 4 mm, the latter ones show systematic errors.

The robustness of position solutions is also very important in PPP besides the positioning accuracy. When the observations on B2 frequency are poorly tracked or contaminated, the benefits will be more significant after adding B3 observations to the B1/B2 PPP processing. In this paper, we only consider the ambiguity-float PPP solutions. It is expected that the ambiguity resolution will benefit from the extra frequency. Given that high-accuracy and reliable float solutions can be achieved by the triple-frequency PPP developed here, the triple-frequency PPP with AR can be investigated based on this.

For completeness, the datasets used for accuracy statistics are re-computed after adding P₁/P₃ ionospheric-free combined code observations to triple-frequency PPP processing. The code-specific IFCB is obtained using the DCB products, which are provided by German Space Operations Center. The average positioning accuracy and convergence time for all 24-h cases are calculated and listed in

Table 8. Positioning accuracy and convergence time for triple-frequency PPP ignoring P₁/P₃ code observations as well as triple-frequency PPP using P₁/P₃ code observations and code-specific IFCB corrections.

Item	Direction	Without P1/P3	With P1/P3
Positioning Accuracy (cm)	East	1.5	1.5
	North	0.3	0.3
	Vertical	1.8	1.7
Convergence Time (min)	East	60.0	57.6
	North	34.0	32.9
	Vertical	87.8	84.2

. For comparison, the results for the triple-frequency PPP developed here are also given in Table 8. After adding P₁/P₃ code observations, the convergence time shows a decrease of 1.1–3.6 min in three directions, but no significant change is found for the positioning accuracy. Greater benefits from P₁/P₃ code observations for triple-frequency PPP can be expected as long as the code-specific IFCB is thoroughly investigated and precisely estimated.

4. Discussion

The GNSS of the future will feature the combination of multi-constellation and multi-frequency signals. In this paper, we focus on triple-frequency integration. A key issue in triple-frequency PPP is to align the satellite clocks, namely IFCB consideration. The IFCB of GPS Block IIF satellites has been investigated by many researchers in terms of sources, dependence, periods, prediction, modeling, variations and amplitude limits [13,14,20,21]. The GPS multipath, which can be extracted using the ionospheric-free geometric linear combination, is a function of satellite elevation angle and antenna height, etc. [25,26,27]. The multipath effects should be considered during the IFCB estimation with the use of DIF measurements consisting of two different ionospheric-free carrier phase combinations. Full consistency of three carriers can be ensured for QZSS and Galileo, and thus the IFCB in multi-frequency integrated precise positioning can be ignored for them [15,16,17]. Several studies also relate to the IFCB of BDS-2 satellites [18,19]. Compared with their results, a wider range of IFCB variations is obtained because the datasets spanning a longer period of time are involved in the analysis. In addition, some initial results are presented, including the analysis of cross-correlation and prediction for real-time precise positioning users as well as the IFCB of BDS-3 satellites. Guo et al. [5] implemented the triple-frequency PPP with BDS data for the first time. However, the additional frequency had a marginal effect on the positioning accuracy in their results, likely because they neglected the effects of IFCB. By contrast, the triple-frequency PPP solutions here achieve higher positioning accuracy in comparison to dual-frequency PPP solutions. The consideration of the triple-frequency measurements for PPP for any satellite system was also discussed in the literature [40], which shows that one can model the triple-frequency code biases, and rigorously provide them for the PPP users for positioning. The difference between the two literatures on triple-frequency PPP is that another S-basis (datum) has been used in Odijk et al. [40], but one can transform between any S-basis choices through an S-transformation. Moreover, the code observations were also rigorously taken into account so as to maximize the redundancy of the models in the literature [40], which is a limitation for triple-frequency PPP model developed in this paper.

According to the results shown in Figure 6, the IFCB estimates of BDS-2 satellites are at a level of several centimeters and exhibit higher noise level, which may limit the applications of IFCB. There are two ways to solve this issue. One way is to increase the number of stations with the capability of offering B1/B2/B3 BDS-2 tracking since the accuracy and reliability of IFCB estimates are mainly determined by the station number in the network. The other way is to develop the efficient undifferenced estimation approach for IFCB because the ED strategy will generate accumulated error. The ED IFCB estimate of a satellite may be inaccurate at an epoch because of the effects of measurement noises when the number of stations that can track the satellite at the epoch is not sufficient. In addition, the gross errors have also effect on the ED IFCB estimation if the data quality check processing does not remove all of them. The error in ED IFCB estimate at the epoch will be introduced into the IFCB estimates at all subsequent epochs due to accumulation. Likewise, the latter epochs may also show similar behavior. As a result, the IFCB estimates will exhibit drifting, such as the IFCB estimates of C15 shown in Figure 6. The ED strategy is suitable for GPS as the peak-to-peak amplitudes of single-day IFCB series can be up to 0.269 m [20].

5. Conclusions

The BDS is providing signals on three or more frequencies. In multi-frequency PPP, a key issue is to estimate the high-accuracy IFCB. Datasets collected at 35 globally distributed stations are employed to analyze the characteristics of IFCB. Considering the effects of IFCB, a triple-frequency PPP model is developed. In the developed model, the ionospheric-free combined observations of L₁/L₂, L₁/L₃ and P₁/P₂ are employed. The GPS corrections of receiver PCO and PCV are simply used for BDS signals. As to other data processing models and strategies, they are the same as those usually adopted in PPP. The triple-frequency PPP developed here can achieve a positioning accuracy better than 2 cm for all three coordinate components. The limitation of the developed model is that the P₁/P₃ ionospheric-free combined code observations are not applied due to the lack of carefully considering the code hardware bias in IFCB estimation. The effects of stability of code hardware bias as well as the influence of SICB on its estimation need further investigation.

The time series of B1/B2a/B3, B1/B2b/B3, B1C/B2a/B3 and B1C/B2b/B3 triple-carrier combinations are used to investigate the IFCB of BDS-3 satellites. The results indicate that no significant IFCB variations can be observed for BDS-3 satellites. In addition, the carrier phase noise and multipath errors with a varying range of 1–4 mm for BDS-3 satellites are comparable to those of BDS-2 satellites. As to BDS-2 satellites, the IFCB between B1/B2 and B1/B3 satellite clocks is investigated and the IFCB variations are generally confined to peak amplitudes of about 5 cm. Moreover, the IFCB time series of BDS-2 satellites show periodic variations, and the prediction accuracy of IFCB is 1.2 cm. The triple-frequency PPP improves the positioning accuracy by 12%, 25% and 10% over the B1/B2 PPP in the east, north and vertical coordinate components, respectively. Future work includes the development of the efficient undifferenced estimation approach to obtain the more precise phase-specific IFCB, which is a linear combination of phase biases at the satellite. In addition, the estimation approach for the code-specific IFCB, which is a linear combination of code hardware biases at the satellite, needs further investigation. We will also devote ourselves to the triple-frequency PPP ambiguity resolution. The PPP of the future will feature the joint use of multi-frequency signals as well as multi-constellation signals.