Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. Field Data Collection
2.2.1. Plant Physiological Measurements
2.2.2. Hyperspectral Reflectance Measurements
2.3. Methods
2.3.1. Selection of Spectral Indices and Sensitive Bands
2.3.2. Multivariate Method
2.3.3. Sensitivity Analysis for Early Stress Detection
2.3.4. Statistical Analyses
3. Results
3.1. Vineyard Weather Condition and Physiological Responses of Grapevines to Induced Water Stress
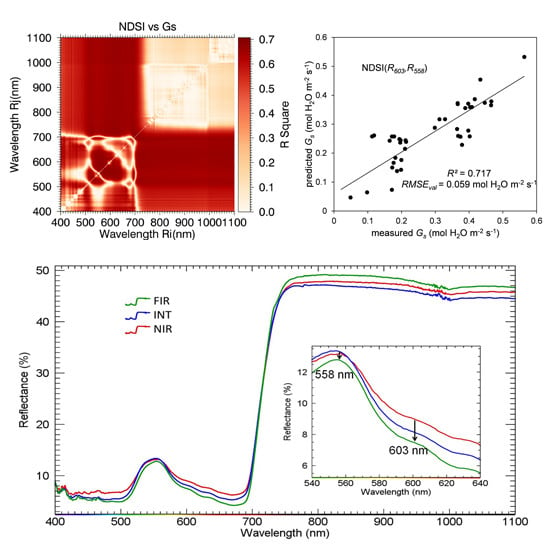
3.2. Complete-Combination Indices Analysis of the Hyperspectral Reflectance Factor Data
3.3. The Relationship between the Grapevine Water Stress Response and Hyperspectral Reflectance Indices from the Literature
3.4. PLSR Analysis
3.5. Feasibility of Early Stress Detection
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Turral, H.; Burke, J.; Faurès, J.M. Climate Change, Water and Food Security; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2011. [Google Scholar]
- Hsiao, T.; Fereres, E.; Acevedo, E.; Henderson, D. Water stress and dynamics of growth and yield of crop plants. In Water and Plant Life; Springer: Berlin, Germany, 1976; pp. 281–305. [Google Scholar]
- Vivier, M.A.; Pretorius, I.S. Genetically tailored grapevines for the wine industry. Trends Biotechnol. 2002, 20, 472–478. [Google Scholar] [CrossRef]
- Stonebridge Research Group. The Economic Impact of Wine and Grape in Missouri; Stonebridge Research Group™ LLC: St.Helena, CA, USA, 2010; p. 26. [Google Scholar]
- Dai, A. Drought under global warming: A review. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Chaves, M. Effects of water deficits on carbon assimilation. J. Exp. Bot. 1991, 42, 1–16. [Google Scholar] [CrossRef]
- Jackson, R.D.; Idso, S.; Reginato, R.; Pinter, P. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
- Krause, G.H. Photoinhibition of photosynthesis. An evaluation of damaging and protective mechanisms. Physiol. Plant. 1988, 74, 566–574. [Google Scholar] [CrossRef]
- Baker, N.R.; Rosenqvist, E. Applications of chlorophyll fluorescence can improve crop production strategies: An examination of future possibilities. J. Exp. Bot. 2004, 55, 1607–1621. [Google Scholar] [CrossRef] [PubMed]
- Lisar, S.Y.; Motafakkerazad, R.; Hossain, M.M.; Rahman, I.M. Water Stress in Plants: Causes, Effects and Responses; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Lim, P.; Nam, H. Aging and senescence of the leaf organ. J. Plant Biol. 2007, 50, 291–300. [Google Scholar] [CrossRef]
- Lichtenthaler, H.K. The stress concept in plants: An introduction. Ann. N. Y. Acad. Sci. 1998, 851, 187–198. [Google Scholar] [CrossRef] [PubMed]
- Bouman, B.; Van Keulen, H.; Van Laar, H.; Rabbinge, R. The ‘school of de wit’crop growth simulation models: A pedigree and historical overview. Agric. Syst. 1996, 52, 171–198. [Google Scholar] [CrossRef]
- Thenkabail, A.; Lyon, P.S.; Huete, J.G. Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Clevers, J.G.; Kooistra, L.; Schaepman, M.E. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth Obs. Geoinform. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A. Sensitivity to foliar anthocyanin content of vegetation indices using green reflectance. IEEE Geosci. Remote Sens. 2011, 8, 464–468. [Google Scholar] [CrossRef]
- Jensen, J.R. Remote Sensing of the Environment: An Earth Resource Perspective 2/e; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Elvidge, C.D. Visible and near infrared reflectance characteristics of dry plant materials. Int. J. Remote Sens. 1990, 11, 1775–1795. [Google Scholar] [CrossRef]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Smith, R.B.; De Pauw, E. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens. Environ. 2000, 71, 158–182. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Teluguntla, P.G.; Gumma, M.K.; Dheeravath, V. Hyperspectral Remote Sensing for Terrestrial Applications. Land Resources Monitoring, Modeling, and Mapping with Remote Sensing; CRC Press: Boca Raton, FL, USA, 2015; pp. 201–233. [Google Scholar]
- Panigada, C.; Rossini, M.; Meroni, M.; Cilia, C.; Busetto, L.; Amaducci, S.; Boschetti, M.; Cogliati, S.; Picchi, V.; Pinto, F. Fluorescence, pri and canopy temperature for water stress detection in cereal crops. Int. J. Appl. Earth Obs. Geoinform. 2014, 30, 167–178. [Google Scholar] [CrossRef]
- Gamon, J.; Penuelas, J.; Field, C. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Suárez, L.; Zarco-Tejada, P.J.; Berni, J.A.; González-Dugo, V.; Fereres, E. Modelling pri for water stress detection using radiative transfer models. Remote Sens. Environ. 2009, 113, 730–744. [Google Scholar] [CrossRef]
- Krause, G.H.; Weis, E. Chlorophyll fluorescence as a tool in plant physiology. Photosynth. Res. 1984, 5, 139–157. [Google Scholar] [CrossRef] [PubMed]
- Guanter, L.; Rossini, M.; Colombo, R.; Meroni, M.; Frankenberg, C.; Lee, J.-E.; Joiner, J. Using field spectroscopy to assess the potential of statistical approaches for the retrieval of sun-induced chlorophyll fluorescence from ground and space. Remote Sens. Environ. 2013, 133, 52–61. [Google Scholar] [CrossRef]
- Guanter, L.; Zhang, Y.; Jung, M.; Joiner, J.; Voigt, M.; Berry, J.A.; Frankenberg, C.; Huete, A.R.; Zarco-Tejada, P.; Lee, J.-E. Global and time-resolved monitoring of crop photosynthesis with chlorophyll fluorescence. Proc. Natl. Acad. Sci. USA 2014, 111, E1327–E1333. [Google Scholar] [CrossRef] [PubMed]
- Moya, I.; Camenen, L.; Evain, S.; Goulas, Y.; Cerovic, Z.G.; Latouche, G.; Flexas, J.; Ounis, A. A new instrument for passive remote sensing: 1. Measurements of sunlight-induced chlorophyll fluorescence. Remote Sens. Environ. 2004, 91, 186–197. [Google Scholar] [CrossRef]
- Meroni, M.; Rossini, M.; Guanter, L.; Alonso, L.; Rascher, U.; Colombo, R.; Moreno, J. Remote sensing of solar-induced chlorophyll fluorescence: Review of methods and applications. Remote Sens. Environ. 2009, 113, 2037–2051. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berni, J.A.; Suárez, L.; Sepulcre-Cantó, G.; Morales, F.; Miller, J.R. Imaging chlorophyll fluorescence with an airborne narrow-band multispectral camera for vegetation stress detection. Remote Sens. Environ. 2009, 113, 1262–1275. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A. Fluorescence, temperature and narrow-band indices acquired from a uav platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Ashourloo, D.; Mobasheri, M.R.; Huete, A. Developing two spectral disease indices for detection of wheat leaf rust (pucciniatriticina). Remote Sens. 2014, 6, 4723–4740. [Google Scholar] [CrossRef]
- Delalieux, S.; Auwerkerken, A.; Verstraeten, W.W.; Somers, B.; Valcke, R.; Lhermitte, S.; Keulemans, J.; Coppin, P. Hyperspectral reflectance and fluorescence imaging to detect scab induced stress in apple leaves. Remote Sens. 2009, 1, 858–874. [Google Scholar] [CrossRef]
- Inoue, Y.; Peñuelas, J.; Miyata, A.; Mano, M. Normalized difference spectral indices for estimating photosynthetic efficiency and capacity at a canopy scale derived from hyperspectral and co 2 flux measurements in rice. Remote Sens Environ. 2008, 112, 156–172. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Marshall, M.; Thenkabail, P.; Biggs, T.; Post, K. Hyperspectral narrowband and multispectral broadband indices for remote sensing of crop evapotranspiration and its components (transpiration and soil evaporation). Agric. For. Meteorol. 2016, 218, 122–134. [Google Scholar] [CrossRef]
- Pôças, I.; Rodrigues, A.; Gonçalves, S.; Costa, P.M.; Gonçalves, I.; Pereira, L.S.; Cunha, M. Predicting grapevine water status based on hyperspectral reflectance vegetation indices. Remote Sens. 2015, 7, 16460–16479. [Google Scholar] [CrossRef]
- Stagakis, S.; Markos, N.; Sykioti, O.; Kyparissis, A. Monitoring canopy biophysical and biochemical parameters in ecosystem scale using satellite hyperspectral imagery: An application on a phlomis fruticosa mediterranean ecosystem using multiangular chris/proba observations. Remote Sens. Environ. 2010, 114, 977–994. [Google Scholar] [CrossRef]
- Stratoulias, D.; Balzter, H.; Zlinszky, A.; Tóth, V.R. Assessment of ecophysiology of lake shore reed vegetation based on chlorophyll fluorescence, field spectroscopy and hyperspectral airborne imagery. Remote Sens. Environ. 2015, 157, 72–84. [Google Scholar] [CrossRef] [Green Version]
- Asner, G.P.; Martin, R.E.; Anderson, C.B.; Knapp, D.E. Quantifying forest canopy traits: Imaging spectroscopy versus field survey. Remote Sens. Environ. 2015, 158, 15–27. [Google Scholar] [CrossRef]
- Sawut, M.; Ghulam, A.; Tiyip, T.; Zhang, Y.-J.; Ding, J.-L.; Zhang, F.; Maimaitiyiming, M. Estimating soil sand content using thermal infrared spectra in arid lands. Int. J. Appl. Earth Obs. Geoinform. 2014, 33, 203–210. [Google Scholar] [CrossRef]
- Boulesteix, A.-L.; Strimmer, K. Partial least squares: A versatile tool for the analysis of high-dimensional genomic data. Brief. Bioinform. 2006, 8, 32–44. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martens, H.; Martens, M. Analysis of two data tables x and y: Partial least squares regression (plsr). In Multivariate Analysis of Quality: An Introduction; Wiley: London, UK, 2001; pp. 111–125. [Google Scholar]
- Feilhauer, H.; Asner, G.P.; Martin, R.E. Multi-method ensemble selection of spectral bands related to leaf biochemistry. Remote Sens. Environ. 2015, 164, 57–65. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.-M.; Baker, N.R. The relationship between the quantum yield of photosynthetic electron transport and quenching of chlorophyll fluorescence. Biochim. Biophys. Acta (BBA)-Gen. Subj. 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.; Painter, T.; Dangel, S.; Martonchik, J. Reflectance quantities in optical remote sensing—definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef] [PubMed]
- Gitelson, A.A.; Zur, Y.; Chivkunova, O.B.; Merzlyak, M.N. Assessing carotenoid content in plant leaves with reflectance spectroscopy. Photochem. Photobiol. 2002, 75, 272–281. [Google Scholar] [CrossRef]
- Gitelson, A.; Merzlyak, M.N. Quantitative estimation of chlorophyll-a using reflectance spectra: Experiments with autumn chestnut and maple leaves. J. Photochem. Photobiol. B Biol. 1994, 22, 247–252. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.; De Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Penuelas, J.; Frederic, B.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Peñuelas, J.; Gamon, J.; Fredeen, A.; Merino, J.; Field, C. Reflectance indices associated with physiological changes in nitrogen-and water-limited sunflower leaves. Remote Sens. Environ. 1994, 48, 135–146. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the modis vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Rouse, J.W., Jr.; Haas, R.; Schell, J.; Deering, D. Monitoring Vegetation Systems in the Great Plains with Erts. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973. [Google Scholar]
- Gitelson, A.A.; Kaufman, Y.J.; Merzlyak, M.N. Use of a green channel in remote sensing of global vegetation from eos-modis. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar] [CrossRef]
- Guyot, G.; Baret, F.; Major, D. High spectral resolution: Determination of spectral shifts between the red and the near infrared. Int. Arch. Photogramm. Remote Sens. 1988, 11, 750–760. [Google Scholar]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green lai of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Dobrowski, S.; Pushnik, J.; Zarco-Tejada, P.J.; Ustin, S. Simple reflectance indices track heat and water stress-induced changes in steady-state chlorophyll fluorescence at the canopy scale. Remote Sens. Environ. 2005, 97, 403–414. [Google Scholar] [CrossRef]
- Barnes, J.; Balaguer, L.; Manrique, E.; Elvira, S.; Davison, A. A reappraisal of the use of dmso for the extraction and determination of chlorophylls a and b in lichens and higher plants. Environ. Exp. Bot. 1992, 32, 85–100. [Google Scholar] [CrossRef]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef]
- Merton, R.; Huntington, J. In early simulation results of the aries-1 satellite sensor for multi-temporal vegetation research derived from aviris. In Proceedings of the Eighth Annual JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 9–11 Februray 1999; pp. 8–14. [Google Scholar]
- Pen¯ Uelas, J.; Filella, I.; Lloret, P.; Mun¯ OZ, F.; Vilajeliu, M. Reflectance assessment of mite effects on apple trees. Int. J. Remote Sens. 1995, 16, 2727–2733. [Google Scholar] [CrossRef]
- Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
- Haaland, D.M.; Thomas, E.V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Martens, H.; Naes, T. Multivariate Calibration; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Wold, S.; Sjöström, M.; Eriksson, L. Pls-regression: A basic tool of chemomrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Eriksson, L. Introduction to Multi-and Megavariate Data Analysis Using Projection Methods (Pca & Pls); Umetrics AB: Malmö, Sweden, 1999. [Google Scholar]
- Flexas, J.; Bota, J.; Escalona, J.M.; Sampol, B.; Medrano, H. Effects of drought on photosynthesis in grapevines under field conditions: An evaluation of stomatal and mesophyll limitations. Funct. Plant Biol. 2002, 29, 461–471. [Google Scholar] [CrossRef]
- Gollan, T.; Turner, N.; Schulze, E.-D. The responses of stomata and leaf gas exchange to vapour pressure deficits and soil water content. Oecologia 1985, 65, 356–362. [Google Scholar] [CrossRef] [PubMed]
- Socias, X.; Correia, M.; Chaves, M.; Medrano, H. The role of abscisic acid and water relations in drought responses of subterranean clover. J. Exp. Bot. 1997, 48, 1281–1288. [Google Scholar] [CrossRef]
- Hunt, E.R., Jr.; Daughtry, C.S.; Li, L. Feasibility of estimating leaf water content using spectral indices from worldview-3’s near-infrared and shortwave infrared bands. Int. J.Remote Sens. 2016, 37, 388–402. [Google Scholar] [CrossRef]
- Ghulam, A.; Li, Z.-L.; Qin, Q.; Tong, Q.; Wang, J.; Kasimu, A.; Zhu, L. A method for canopy water content estimation for highly vegetated surfaces-shortwave infrared perpendicular water stress index. Sci. China Ser. D Earth Sci. 2007, 50, 1359–1368. [Google Scholar] [CrossRef]
- Chen, J.; Gu, S.; Shen, M.; Tang, Y.; Matsushita, B. Estimating aboveground biomass of grassland having a high canopy cover: An exploratory analysis of in situ hyperspectral data. Int. J.Remote Sens. 2009, 30, 6497–6517. [Google Scholar] [CrossRef]
- Cho, M.A.; Skidmore, A.; Corsi, F.; Van Wieren, S.E.; Sobhan, I. Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression. Int. J. Appl. Earth Obs. Geoinform. 2007, 9, 414–424. [Google Scholar] [CrossRef]
- Cowan, I.; Farquhar, G. Stomatal Functioning in Relation to Leaf Metabolism and Environment. In Integration of Activity in the Higher Plant; Cambridge University Press: Cambridge, UK, 1977; pp. 471–505. [Google Scholar]
- Anjum, S.A.; Xie, X.-Y.; Wang, L.-C.; Saleem, M.F.; Man, C.; Lei, W. Morphological, physiological and biochemical responses of plants to drought stress. Afr. J. Agric. Res. 2011, 6, 2026–2032. [Google Scholar]
- Chaves, M.M.; Maroco, J.P.; Pereira, J.S. Understanding plant responses to drought—From genes to the whole plant. Funct. Plant Biol. 2003, 30, 239–264. [Google Scholar] [CrossRef]
- Xu, Z.; Zhou, G. Responses of leaf stomatal density to water status and its relationship with photosynthesis in a grass. J. Exp. Bot. 2008, 59, 3317–3325. [Google Scholar] [CrossRef] [PubMed]
- Zarco-Tejada, P.J.; Ca talina, A.; González, M.; Martín, P. Relationships between net photosynthesis and steady-state chlorophyll fluorescence retrieved from airborne hyperspectral imagery. Remote Sens. Environ. 2013, 136, 247–258. [Google Scholar] [CrossRef]
- Flexas, J.; Escalona, J.M.; Evain, S.; Gulías, J.; Moya, I.; Osmond, C.B.; Medrano, H. Steady-state chlorophyll fluorescence (fs) measurements as a tool to follow variations of net co2 assimilation and stomatal conductance during water-stress in c3 plants. Physiol. Plant. 2002, 114, 231–240. [Google Scholar] [CrossRef] [PubMed]
- Sellers, P.; Berry, J.; Collatz, G.; Field, C.; Hall, F. Canopy reflectance, photosynthesis, and transpiration. Iii. A reanalysis using improved leaf models and a new canopy integration scheme. Remote Sens. Environ. 1992, 42, 187–216. [Google Scholar] [CrossRef]
- Myneni, R.; Ganapol, B.; Asrar, G. Remote sensing of vegetation canopy photosynthetic and stomatal conductance efficiencies. Remote Sens. Environ. 1992, 42, 217–238. [Google Scholar] [CrossRef]
- Verma, S.; Sellers, P.; Walthall, C.; Hall, F.; Kim, J.; Goetz, S. Photosynthesis and stomatal conductance related to reflectance on the canopy scale. Remote Sens. Environ. 1993, 44, 103–116. [Google Scholar] [CrossRef]
- Carter, G.A. Reflectance wavebands and indices for remote estimation of photosynthesis and stomatal conductance in pine canopies. Remote Sens. Environ. 1998, 63, 61–72. [Google Scholar] [CrossRef]
- Davies, W.J.; Zhang, J. Root signals and the regulation of growth and development of plants in drying soil. Ann. Rev. Plant Biol. 1991, 42, 55–76. [Google Scholar] [CrossRef]
- Matsumoto, K.; Ohta, T.; Tanaka, T. Dependence of stomatal conductance on leaf chlorophyll concentration and meteorological variables. Agric. For. Meteorol. 2005, 132, 44–57. [Google Scholar] [CrossRef]
- Medrano, H.; Escalona, J.M.; Bota, J.; Gulías, J.; Flexas, J. Regulation of photosynthesis of c3 plants in response to progressive drought: Stomatal conductance as a reference parameter. Ann. Bot. 2002, 89, 895–905. [Google Scholar] [CrossRef] [PubMed]
- Oren, R.; Sperry, J.S.; Katul, G.; Pataki, D.E.; Ewers, B.; Phillips, N.; Schäfer, K. Survey and synthesis of intra-and interspecific variation in stomatal sensitivity to vapour pressure deficit. Plant Cell Environ. 1999, 22, 1515–1526. [Google Scholar] [CrossRef]
- Bowman, W.D. The relationship between leaf water status, gas exchange, and spectral reflectance in cotton leaves. Remote Sens. Environ. 1989, 30, 249–255. [Google Scholar] [CrossRef]
- Maas, S.; Dunlap, J. Reflectance, transmittance, and absorptance of light by normal, etiolated, and albino corn leaves. Agron. J. 1989, 81, 105–110. [Google Scholar] [CrossRef]
- Adams, M.L.; Philpot, W.D.; Norvell, W.A. Yellowness index: An application of spectral second derivatives to estimate chlorosis of leaves in stressed vegetation. Int. J.Remote Sens. 1999, 20, 3663–3675. [Google Scholar] [CrossRef]
- Globe, D. The Benefits of the 8 Spectral Bands of Worldview-2; White Paper; Digital Globe: Westminster, CO, USA, 2009; Volume 12. [Google Scholar]
- Zengeya, F.M.; Mutanga, O.; Murwira, A. Linking remotely sensed forage quality estimates from worldview-2 multispectral data with cattle distribution in a savanna landscape. Int. J. Appl. Earth Obs. Geoinform. 2013, 21, 513–524. [Google Scholar] [CrossRef]
- McMurtrey, J.; Chappelle, E.; Kim, M.; Meisinger, J.; Corp, L. Distinguishing nitrogen fertilization levels in field corn (Zea mays L.) with actively induced fluorescence and passive reflectance measurements. Remote Sens. Environ. 1994, 47, 36–44. [Google Scholar] [CrossRef]
- Yoder, B.J.; Waring, R.H. The normalized difference vegetation index of small douglas-fir canopies with varying chlorophyll concentrations. Remote Sens. Environ. 1994, 49, 81–91. [Google Scholar] [CrossRef]
- Buschmann, C.; Langsdorf, G.; Lichtenthaler, H. Imaging of the blue, green, and red fluorescence emission of plants: An overview. Photosynthetica 2001, 38, 483–491. [Google Scholar] [CrossRef]
- Papageorgiou, G.C. Chlorophyll A Fluorescence: A Signature of Photosynthesis; Springer Science & Business Media: Berlin, Germany, 2007; Volume 19. [Google Scholar]
- Gitelson, A.A.; Buschmann, C.; Lichtenthaler, H.K. Leaf chlorophyll fluorescence corrected for re-absorption by means of absorption and reflectance measurements. J. Plant Physiol. 1998, 152, 283–296. [Google Scholar] [CrossRef]
- Lichtenthaler, H.; Wenzel, O.; Buschmann, C.; Gitelson, A. Plant stress detection by reflectance and fluorescencea. Ann. N. Y. Acad.Sci. 1998, 851, 271–285. [Google Scholar] [CrossRef]
- Demmig-Adams, B.; Adams, W.W. The role of xanthophyll cycle carotenoids in the protection of photosynthesis. Trends Plant Sci. 1996, 1, 21–26. [Google Scholar] [CrossRef]
- Flexas, J.; Escalona, J.; Medrano, H. Water stress induces different levels of photosynthesis and electron transport rate regulation in grapevines. Plant Cell Environ. 1999, 22, 39–48. [Google Scholar] [CrossRef]
- Gamon, J.A.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef] [PubMed]
- Penuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
- Wong, C.; Gamon, J.A. Three causes of variation in the photochemical reflectance index (pri) in evergreen conifers. New Phytol. 2015, 206, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Hilker, T.; Coops, N.C.; Hall, F.G.; Black, T.A.; Wulder, M.A.; Nesic, Z.; Krishnan, P. Separating physiologically and directionally induced changes in pri using brdf models. Remote Sens. Environ. 2008, 112, 2777–2788. [Google Scholar] [CrossRef]
- Barton, C.; North, P. Remote sensing of canopy light use efficiency using the photochemical reflectance index: Model and sensitivity analysis. Remote Sens. Environ. 2001, 78, 264–273. [Google Scholar] [CrossRef]
- Evans, J.R. The allocation of protein nitrogen in the photosynthetic apparatus: Costs, consequences and control. In Photosynthesis; Alan R. Liss Inc.: New York, NY, USA, 1989; pp. 183–205. [Google Scholar]
- Inoue, Y.; Guérif, M.; Baret, F.; Skidmore, A.; Gitelson, A.; Schlerf, M.; Darvishzadeh, R.; Olioso, A. Simple and robust methods for remote sensing of canopy chlorophyll content: A comparative analysis of hyperspectral data for different types of vegetation. Plant Cell Environ. 2016, 39, 2609–2623. [Google Scholar] [CrossRef] [PubMed]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Hansen, P.; Schjoerring, J. Reflectance measurement of canopy biomass and nitrogen status in wheat crops using normalized difference vegetation indices and partial least squares regression. Remote Sens. Environ. 2003, 86, 542–553. [Google Scholar] [CrossRef]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Doktor, D.; Lausch, A.; Spengler, D.; Thurner, M. Extraction of plant physiological status from hyperspectral signatures using machine learning methods. Remote Sens. 2014, 6, 12247–12274. [Google Scholar] [CrossRef]








| Reflectance Index | Acronym | Equation | References |
|---|---|---|---|
| Leaf pigment | |||
| Anthocyanin (Gitelson) | AntGitelson | AntGitelson = (1/R550 − 1/R700) × R780 | [48] |
| Carotenoid Reflectance Index | CRI1 | CRI1 = 1/R510 − 1/R550 | [49] |
| Carotenoid Reflectance Index | CRI2 | CRI2 = 1/R510 − 1/R700 | [49] |
| Chlorophyll Index | CI | CI = (R750 − R705)/(R750 + R705) | [50] |
| Optimized Soil-Adjusted Vegetation Index | OSAVI | OSAVI = (1 + 0.16) × (R800 − R670)/(R800 + R670 + 0.16) | [51] |
| Red Green Index | RGI | RGI = R690/R550 | [52] |
| Structure Intensive Pigment Index | SIPI | SIPI = (R800 − R450)/(R800 + R650) | [53] |
| Transformed Chlorophyll Absorption in Reflectance Index | TCARI | TCARI = 3 × ((R700 − R670) − 0.2 × (R700 − R550) × (R700/R670)) | [54] |
| TCARI/OSAVI | TCARI/OSAVI | [54] | |
| Normalized Pigment Chlorophyll Index | NPCI | NPCI = (R680 − R430)/(R680 + R430) | [55] |
| Greenness | |||
| Enhanced Vegetation Index EVI | EVI | (2.5(R782 − R 675)/(R782 + 6 × R675 − 7.5 × R445 + 1)) | [56] |
| Normalized Difference Vegetation Index | NDVI | NDVI = (R800 − R670)/(R800 + R670) | [57] |
| Greenness Index | GI | GI = R554/R677 | [52] |
| Green NDVI | GNDVI | GNDVI = (R750 − R540 + R570)/(R750 + R540 − R570) | [58] |
| Red Edge Inflection Point | REIP | REIP = 700 + 40 × {[(R670 + R780)/2 − R700]/(R740 − R700)} | [59] |
| Simple Ratio | SR | SR = R900/R680 | [57] |
| Triangular Vegetation Index | TVI | TVI = 0.5 × (120 × (R750 − R550) − 200 × (R670 − R550)) | [60] |
| Stress | |||
| Fluorescence Ratio Index 1 | FRI1 | FRI1 = R690/R600 | [61] |
| Fluorescence Ratio Indices 2 | FRI2 | FRI2 = R740/R800 | [61] |
| Modified Red Edge Simple Ratio Index | mRESR | mRESR = (R750 − R445)/(R705 + R445) | [20] |
| Normalized Phaeophytinization Index | NPQI | NPQI = (R415 − R435)/(R415 + R435) | [62] |
| Photochemical Reflectance Index | PRI | PRI = (R531 − R570)/(R531 + R570) | [24] |
| Plant Senescence Reflectance Index | PSRI | PSRI = (R680−R500)/R750 | [63] |
| Red-Edge Vegetation Stress Index | RVSI | 0.5(R722 + R763) − R733 | [64] |
| Simple Ratio Pigment Index | SRPI | SRPI = R430/R680 | [65] |
| Water | |||
| Water Index | WI | WI = R900/R970 | [66] |
| 18 June 2014 | Gs | Ai | Fs | Fm' | ΔF/Fm' | ETR | qP | NPQ |
| FIR (n = 12) | 0.37 | 20.3 | 811 | 1221 | 0.33 | 145 | 0.64 | 5.19 |
| INT (n = 12) | 0.31 | 19.7 | 800 | 1183 | 0.32 | 140 | 0.62 | 5.53 |
| NIR (n = 8) | 0.39 | 20.1 | 784 | 1211 | 0.35 | 153 | 0.67 | 5.18 |
| RMSE | 0.08 | 3.38 | 84 | 145 | 0.04 | 17 | 0.04 | 0.90 |
| Significance level | ns. | ns. | ns. | ns. | ns. | ns. | ns. | ns. |
| 19 August 2014 | ||||||||
| FIR (n = 12) | 0.17a | 21.1a | 827a | 1213a | 0.32a | 139a | 0.63 | 5.00a |
| INT (n = 12) | 0.06b | 16.0b | 768b | 1067b | 0.28b | 121b | 0.59 | 5.89b |
| NIR (n = 12) | 0.04b | 15.4b | 721b | 983b | 0.26b | 115b | 0.57 | 6.46b |
| RMSE | 0.04 | 3.4 | 54 | 94 | 0.04 | 20 | 0.07 | 0.59 |
| Significance level | *** | ** | *** | *** | * | * | ns | *** |
| 10 July 2015 | ||||||||
| FIR (n = 24) | 0.30 | 7.88 | 694 | 962 | 0.27 | 117 | 0.57 | 1.88 |
| INT (n = 24) | 0.33 | 7.35 | 711 | 1006 | 0.28 | 124 | 0.59 | 1.93 |
| NIR (n = 24) | 0.33 | 9.45 | 694 | 967 | 0.27 | 117 | 0.57 | 1.87 |
| RMSE | 0.08 | 3.85 | 83 | 180 | 0.07 | 32 | 0.10 | 0.2 |
| Significance level | ns. | ns. | ns. | ns. | ns. | ns. | ns. | ns. |
| 21 September 2015 | ||||||||
| FIR (n = 24) | 0.19 | 17.4 | 955 | 1359 | 0.29 | 128 | 0.56 | 2.10 |
| INT (n = 24) | 0.18 | 17.0 | 1008 | 1408 | 0.29 | 125 | 0.54 | 2.12 |
| NIR (n = 24) | 0.18 | 17.3 | 921 | 1369 | 0.32 | 140 | 0.61 | 2.13 |
| RMSE | 0.03 | 3.8 | 172 | 219 | 0.07 | 32 | 0.11 | 0.21 |
| Significance level | ns. | ns. | ns. | ns. | ns. | ns. | ns. | ns. |
| Gs | Ai | Fs | Fm' | ΔF/Fm' | ETR | qP | NPQ | |
|---|---|---|---|---|---|---|---|---|
| 18 June 2014 | ||||||||
| Gs | 1.00 | |||||||
| Ai | 0.75 ** | 1.00 | ||||||
| Fs | 0.05 | 0.21 | 1.00 | |||||
| Fm' | 0.27 | 0.37 ** | 0.85 ** | 1.00 | ||||
| ΔF/Fm' | 0.39 * | 0.34 | 0.05 | 0.56 ** | 1.00 | |||
| ETR | 0.39 * | 0.34 | 0.05 | 0.56 ** | 0.99 ** | 1.00 | ||
| qP | 0.26 | 0.06 | −0.32 | 0.16 * | 0.85 ** | 0.85 ** | 1.00 | |
| NPQ | −0.23 | −0.31 | −0.82** | −0.97 ** | −0.59 ** | −0.59 ** | −0.26 | 1.00 |
| 19 August 2014 | ||||||||
| Gs | 1.00 | |||||||
| Ai | 0.82 ** | 1.00 | ||||||
| Fs | 0.47 ** | 0.29 | 1.00 | |||||
| Fm' | 0.50 ** | 0.34 * | 0.82 ** | 1.00 | ||||
| ΔF/Fm' | 0.26 | 0.22 | 0.15 | 0.68 ** | 1.00 | |||
| ETR | 0.14 | 0.22 | 0.15 | 0.69 ** | 0.99 ** | 1.00 | ||
| qP | 0.13 | 0.14 | −0.05 | 0.51 ** | 0.96 ** | 0.96 ** | 1.00 | |
| NPQ | −0.50 | −0.31 | −0.81 ** | −0.99 ** | −0.69 ** | −0.69 ** | −0.53 ** | 1.00 |
| 10 July 2015 | ||||||||
| Gs | 1.00 | |||||||
| Ai | 0.31 ** | 1.00 | ||||||
| Fs | −0.01 | −0.08 | 1.00 | |||||
| Fm' | −0.10 | 0.00 | 0.87 ** | 1.00 | ||||
| ΔF/Fm' | −0.18 | −0.10 | 0.40 ** | 0.84 * | 1.00 | |||
| ETR | 0.19 | −0.10 | 0.48 ** | 0.84 ** | 0.99 ** | 1.00 | ||
| qP | −0.22 | −0.14 | 0.24 * | 0.66 ** | 0.95 ** | 0.95 ** | 1.00 | |
| NPQ | −0.12 | −0.04 | 0.74 ** | 0.96 ** | 0.91 ** | 0.91 ** | 0.75 ** | 1.00 |
| 21 September 2015 | ||||||||
| Gs | 1.00 | |||||||
| Ai | 0.76 ** | 1.00 | ||||||
| Fs | 0.11 | −0.10 | 1.00 | |||||
| Fm' | 0.29 * | 0.10 | 0.79 ** | 1.00 | ||||
| ΔF/Fm' | 0.26 * | 0.31 ** | −0.39 ** | 0.25 * | 1.00 | |||
| ETR | 0.26 * | 0.31 ** | −0.39 ** | 0.25 ** | 1.00 ** | 1.00 | ||
| qP | 0.18 | 0.29 * | −0.65 ** | −0.06 * | 0.93 ** | 0.93 ** | 1.00 | |
| NPQ | 0.31 ** | 0.20 | 0.37 ** | 0.82 ** | 0.63 ** | 0.63 ** | 0.31 ** | 1.00 |
| Spectral Indices | Gs | Ai | Fs | Fm' | NPQ |
|---|---|---|---|---|---|
| R2 (RMSEcal) | R2 (RMSEcal) | R2 (RMSEcal) | R2 (RMSEcal) | R2 (RMSEcal) | |
| NDSI(603,558) | 0.720 (0.063) | - | - | - | - |
| NDSI(728,525) | 0.711 (0.066) | - | - | - | - |
| NDSI(830,525) | 0.703 (0.068) | - | - | - | - |
| NDSI(1000,525) | 0.694 (0.068) | - | - | - | - |
| NDSI(715,620) | 0.715 (0.066) | - | - | - | - |
| NDSI(818,620) | 0.707 (0.067) | - | - | - | - |
| NDSI(1000,620) | 0.709 (0.067) | - | - | - | - |
| NDSI(726,630) | 0.714 (0.068) | - | - | - | - |
| NDSI(778,635) | 0.707 (0.069) | - | - | - | - |
| NDSI(1000,635) | 0.707 (0.070) | - | - | - | - |
| NDSI(705,535) | - | 0.256 (5.268) | - | - | - |
| - | |||||
| NDSI(704,540) | - | - | 0.275 (140.281) | - | - |
| NDSI(704,540) | - | - | - | 0.284 (208.748) | - |
| NDSI(685,415) | - | - | - | - | 0.681 (0.992) |
| Gs | NPQ | |
|---|---|---|
| R2 (RMSEcal) | R2 (RMSEcal) | |
| Leaf Pigment | ||
| AntGitelson | 0.567 (0.100) *** | 0.269 (1.509) *** |
| CRI1 | 0.663 (0.087) *** | 0.332 (1.441) *** |
| CRI2 | 0.648 (0.090) *** | 0.207 (1.571) *** |
| CI | 0.648 (0.090) *** | 0.529 (1.211) *** |
| OSAVI | 0.662 (0.088) *** | 0.485 (1.261) *** |
| RGI | 0.592 (0.097) *** | 0.364 (1.407) *** |
| SIPI | 0.632 (0.092) *** | 0.376 (1.394) *** |
| TCARI | 0.537 (0.103) *** | 0.368 (1.403) *** |
| TCARI/OSAVI | 0.587 (0.098) *** | 0.433 (1.327) *** |
| NPCI | 0.518 (0.106) *** | 0.544 (1.191) *** |
| Greenness | ||
| EVI | 0.156 (0.140) ** | 0.038 (1.731) ** |
| NDVI | 0.662 (0.088) *** | 0.529 (1.211) *** |
| GI | 0.277 (0.130) *** | 0.057 (1.714)** |
| GNDVI | 0.218 (0.135) *** | 0.045 (1.724)** |
| REIP | 0.540 (0.104) *** | 0.456 (1.301) *** |
| SR | 0.680 (0.086) *** | 0.531 (1.196) *** |
| TVI | 0.257 (0.131) *** | 0.086 (1.687) *** |
| Stress | ||
| FRI1 | - | 0.046(1.723)** |
| FRI2 | 0.314 (0.126) *** | 0.356 (1.416) *** |
| mRESR | 0.656 (0.089) *** | 0.383 (1.386) *** |
| NPQI | 0.222 (0.134) *** | 0.094 (1.680) *** |
| PRI | 0.022 (0.151) | 0.043 (1.725) ** |
| PSRI | 0.278 (0.130) *** | - |
| RVSI | 0.263 (0.131) | - |
| SRPI | 0.530 (0.105) *** | 0.450 (1.309) *** |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maimaitiyiming, M.; Ghulam, A.; Bozzolo, A.; Wilkins, J.L.; Kwasniewski, M.T. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sens. 2017, 9, 745. https://doi.org/10.3390/rs9070745
Maimaitiyiming M, Ghulam A, Bozzolo A, Wilkins JL, Kwasniewski MT. Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sensing. 2017; 9(7):745. https://doi.org/10.3390/rs9070745
Chicago/Turabian StyleMaimaitiyiming, Matthew, Abduwasit Ghulam, Arianna Bozzolo, Joseph L. Wilkins, and Misha T. Kwasniewski. 2017. "Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy" Remote Sensing 9, no. 7: 745. https://doi.org/10.3390/rs9070745
APA StyleMaimaitiyiming, M., Ghulam, A., Bozzolo, A., Wilkins, J. L., & Kwasniewski, M. T. (2017). Early Detection of Plant Physiological Responses to Different Levels of Water Stress Using Reflectance Spectroscopy. Remote Sensing, 9(7), 745. https://doi.org/10.3390/rs9070745