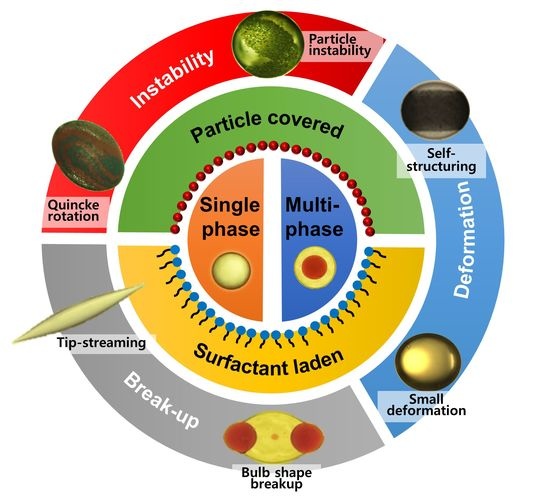
Electro-Hydrodynamics of Emulsion Droplets: Physical Insights to Applications
Abstract
:1. Introduction
2. Approaches Used to Study the Droplet Electrohydrodynamics (EHD)
3. Background and Theory
3.1. Non-Dimensional Parameters
3.2. Govening Equations of Leaky Dielectric Model (LDM)
3.2.1. Electric Field Equations and Their Solutions
3.2.2. Fluid Flow Equations and Their Solutions
3.2.3. Taylor Deformation Parameter ()
3.2.4. Effect of AC Electric Field
4. Single-phase Emulsion Droplets
4.1. Deformation
4.1.1. Under DC Electric Field
4.1.2. Under AC Electric Field
4.2. Instabilities and Breakups
4.2.1. Prolate Deforming Droplets
4.2.2. Oblate Deforming Droplets
5. Particle-Covered Droplets
5.1. Deformation
5.2. Instabilities and Breakups
6. Surfactant-Laden Droplets
6.1. Deformation
6.2. Instabilities and Breakups
7. Multi-Phase Emulsion Droplets
7.1. Deformation
7.2. Instabilities and Breakups
8. Applications
8.1. Mass Production of Micro/Nano Droplets
8.2. Functional Droplet/Particle Synthesis
8.3. Micro-Rotor
8.4. Encapsulation/Target Delivery
9. Conclusions and Future Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Taylor, G. Studies in electrohydrodynamics. I. The circulation produced in a drop by electrical field. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1966, 291, 159–166. [Google Scholar]
- Melcher, J.R.; Taylor, G.I. Electrohydrodynamics: A Review of the Role of Interfacial Shear Stresses. Annu. Rev. Fluid Mech. 1969, 1, 111–146. [Google Scholar] [CrossRef]
- Ajayi, O. A note on Taylor’s electrohydrodynamic theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1978, 364, 499–507. [Google Scholar]
- Das, D.; Saintillan, D. A nonlinear small-deformation theory for transient droplet electrohydrodynamics. J. Fluid Mech. 2017, 810, 225–253. [Google Scholar] [CrossRef] [Green Version]
- Esmaeeli, A.; Sharifi, P. Transient electrohydrodynamics of a liquid drop. Phys. Rev. E 2011, 84, 036308. [Google Scholar] [CrossRef]
- Feng, J.Q.; Scott, T.C. A computational analysis of electrohydrodynamics of a leaky dielectric drop in an electric field. J. Fluid Mech. 1996, 311, 289–326. [Google Scholar] [CrossRef]
- Torza, S.; Cox, R.; Mason, S. Electrohydrodynamic deformation and bursts of liquid drops. Phil. Trans. R. Soc. Lond. A 1971, 269, 295–319. [Google Scholar]
- Bentenitis, N.; Krause, S. Droplet deformation in dc electric fields: The extended leaky dielectric model. Langmuir 2005, 21, 6194–6209. [Google Scholar] [CrossRef]
- Zhang, J.; Zahn, J.D.; Lin, H. Transient solution for droplet deformation under electric fields. Phys. Rev. E 2013, 87, 043008. [Google Scholar] [CrossRef] [Green Version]
- Zholkovskij, E.K.; Masliyah, J.H.; Czarnecki, J. An electrokinetic model of drop deformation in an electric field. J. Fluid Mech. 2002, 472, 1–27. [Google Scholar] [CrossRef]
- Moriya, S.; Adachi, K.; Kotaka, T. Deformation of droplets suspended in viscous media in an electric field. 1. Rate of deformation. Langmuir 1986, 2, 155–160. [Google Scholar] [CrossRef]
- Zabarankin, M. Small deformation theory for two leaky dielectric drops in a uniform electric field. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20190517. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, M.S.; Song, R.; Kim, H.; Lee, J. Multimodal breakup of a double emulsion droplet under an electric field. Soft Matter 2019, 15, 2292–2300. [Google Scholar] [CrossRef]
- Abbasi, M.S.; Song, R.; Kim, J.; Lee, J. Electro-hydrodynamic behavior and interface instability of double emulsion droplets under high electric field. J. Electrost. 2017, 85, 11–22. [Google Scholar] [CrossRef]
- Abbasi, M.S.; Song, R.; Kim, S.M.; Kim, H.; Lee, J. Mono-emulsion droplet stretching under direct current electric field. Soft Matter 2019, 15, 2328–2335. [Google Scholar] [CrossRef] [PubMed]
- Abbasi, M.S.; Song, R.; Lee, J. Breakups of an encapsulated surfactant-laden aqueous droplet under a DC electric field. Soft Matter 2019, 15, 8905–8911. [Google Scholar] [CrossRef] [PubMed]
- Bararnia, H.; Ganji, D. Breakup and deformation of a falling droplet under high voltage electric field. Adv. Powder Technol. 2013, 24, 992–998. [Google Scholar] [CrossRef]
- Brosseau, Q.; Vlahovska, P.M. Streaming from the Equator of a Drop in an External Electric Field. Phys. Rev. Lett. 2017, 119, 034501. [Google Scholar] [CrossRef]
- Collins, R.T.; Jones, J.J.; Harris, M.T.; Basaran, O.A. Electrohydrodynamic tip streaming and emission of charged drops from liquid cones. Nat. Phys. 2008, 4, 149. [Google Scholar] [CrossRef]
- Das, S.; Thaokar, R.M. Large-deformation electrohydrodynamics of an elastic capsule in a DC electric field. J. Fluid Mech. 2018, 841, 489–520. [Google Scholar] [CrossRef] [Green Version]
- Dommersnes, P.; Rozynek, Z.; Mikkelsen, A.; Castberg, R.; Kjerstad, K.; Hersvik, K.; Fossum, J.O. Active structuring of colloidal armour on liquid drops. Nat. Commun. 2013, 4, 2066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubash, N.; Mestel, A.J. Breakup behavior of a conducting drop suspended in a viscous fluid subject to an electric field. Phys. Fluids 2007, 19, 072101. [Google Scholar] [CrossRef]
- Eggleton, C.D.; Tsai, T.-M.; Stebe, K.J. Tip streaming from a drop in the presence of surfactants. Phys. Rev. Lett. 2001, 87, 048302. [Google Scholar] [CrossRef] [Green Version]
- Ha, J.-W.; Yang, S.-M. Deformation and breakup of Newtonian and non-Newtonian conducting drops in an electric field. J. Fluid Mech. 2000, 405, 131–156. [Google Scholar] [CrossRef]
- Ha, J.-W.; Yang, S.-M. Breakup of a multiple emulsion drop in a uniform electric field. J. Colloid Interface Sci. 1999, 213, 92–100. [Google Scholar] [CrossRef] [Green Version]
- Karyappa, R.B.; Deshmukh, S.D.; Thaokar, R.M. Breakup of a conducting drop in a uniform electric field. J. Fluid Mech. 2014, 754, 550–589. [Google Scholar] [CrossRef]
- Luo, X.; Yan, H.; Huang, X.; Yang, D.; Wang, J.; He, L. Breakup characteristics of aqueous droplet with surfactant in oil under direct current electric field. J. Colloid Interface Sci. 2017, 505, 460–466. [Google Scholar] [CrossRef]
- Mikkelsen, A.; Dommersnes, P.; Rozynek, Z.; Gholamipour-Shirazi, A.; Carvalho, M.d.S.; Fossum, J.O.J.M. Mechanics of Pickering drops probed by electric Field–Induced Stress. Materials 2017, 10, 436. [Google Scholar] [CrossRef] [Green Version]
- Mikkelsen, A.; Wojciechowski, J.; Rajňák, M.; Kurimský, J.; Khobaib, K.; Kertmen, A.; Rozynek, Z.J.M. Electric field-driven assembly of sulfonated polystyrene microspheres. Materials 2017, 10, 329. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spasic, A.M.; Jovanovic, J.M.; Manojlovic, V.; Jovanovic, M. Breaking of double emulsions based on electrohydrodynamics principles. J. Colloid Interface Sci. 2016, 479, 165–172. [Google Scholar] [CrossRef]
- Ahn, K.; Kerbage, C.; Hunt, T.P.; Westervelt, R.; Link, D.R.; Weitz, D. Dielectrophoretic manipulation of drops for high-speed microfluidic sorting devices. Appl. Phys. Lett. 2006, 88, 024104. [Google Scholar] [CrossRef] [Green Version]
- Fernández De La Mora, J. The fluid dynamics of Taylor cones. Annu. Rev. Fluid Mech. 2007, 39, 217–243. [Google Scholar] [CrossRef]
- Reznik, S.; Yarin, A.; Zussman, E.; Bercovici, L. Evolution of a compound droplet attached to a core-shell nozzle under the action of a strong electric field. Phys. Fluid 2006, 18, 062101. [Google Scholar] [CrossRef]
- Sankaran, S.; Saville, D. Experiments on the stability of a liquid bridge in an axial electric field. Phys. Fluids A Fluid Dyn. 1993, 5, 1081–1083. [Google Scholar] [CrossRef]
- Geng, H.; Feng, J.; Stabryla, L.M.; Cho, S.K. Dielectrowetting manipulation for digital microfluidics: Creating, transporting, splitting, and merging of droplets. Lab Chip 2017, 17, 1060–1068. [Google Scholar] [CrossRef]
- Jia, Y.; Ren, Y.; Hou, L.; Liu, W.; Deng, X.; Jiang, H. Sequential coalescence enabled two-step microreactions in triple-core double-emulsion droplets triggered by an electric field. Small 2017, 13, 1702188. [Google Scholar] [CrossRef]
- Liu, L.; Yang, J.-P.; Ju, X.-J.; Xie, R.; Liu, Y.-M.; Wang, W.; Zhang, J.-J.; Niu, C.H.; Chu, L.-Y. Monodisperse core-shell chitosan microcapsules for pH-responsive burst release of hydrophobic drugs. Soft Matter 2011, 7, 4821–4827. [Google Scholar] [CrossRef]
- Loscertales, I.G.; Barrero, A.; Guerrero, I.; Cortijo, R.; Marquez, M.; Ganan-Calvo, A. Micro/nano encapsulation via electrified coaxial liquid jets. Science 2002, 295, 1695–1698. [Google Scholar] [CrossRef]
- Mura, S.; Nicolas, J.; Couvreur, P. Stimuli-responsive nanocarriers for drug delivery. Nat. Mater. 2013, 12, 991. [Google Scholar] [CrossRef]
- Seifert, T.; Sowade, E.; Roscher, F.; Wiemer, M.; Gessner, T.; Baumann, R.R. Additive manufacturing technologies compared: Morphology of deposits of silver ink using inkjet and aerosol jet printing. Ind. Eng. Chem. Res. 2015, 54, 769–779. [Google Scholar] [CrossRef]
- Song, R.; Abbasi, M.S.; Lee, J. Fabrication of 3D printed modular microfluidic system for generating and manipulating complex emulsion droplets. Microfluid. Nanofluid. 2019, 23, 92. [Google Scholar] [CrossRef]
- Tucker-Schwartz, A.K.; Bei, Z.; Garrell, R.L.; Jones, T.B. Polymerization of Electric Field-Centered Double Emulsion Droplets to Create Polyacrylate Shells. Langmuir 2010, 26, 18606–18611. [Google Scholar] [CrossRef]
- Xie, J.; Jiang, J.; Davoodi, P.; Srinivasan, M.P.; Wang, C.-H. Electrohydrodynamic atomization: A two-decade effort to produce and process micro-/nanoparticulate materials. Chem. Eng. Sci. 2015, 125, 32–57. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhaumik, S.K.; Roy, R.; Chakraborty, S.; DasGupta, S. Low-voltage electrohydrodynamic micropumping of emulsions. Sens. Actuators B Chem. 2014, 193, 288–293. [Google Scholar] [CrossRef]
- Wehking, J.D.; Kumar, R. Droplet actuation in an electrified microfluidic network. Lab Chip 2015, 15, 793–801. [Google Scholar] [CrossRef]
- Xi, H.-D.; Guo, W.; Leniart, M.; Chong, Z.Z.; Tan, S.H. AC electric field induced droplet deformation in a microfluidic T-junction. Lab Chip 2016, 16, 2982–2986. [Google Scholar] [CrossRef] [PubMed]
- Guan, X.; Hou, L.; Ren, Y.; Deng, X.; Lang, Q.; Jia, Y.; Hu, Q.; Tao, Y.; Liu, J.; Jiang, H. A dual-core double emulsion platform for osmolarity-controlled microreactor triggered by coalescence of encapsulated droplets. Biomicrofluidics 2016, 10, 034111. [Google Scholar] [CrossRef] [Green Version]
- Huo, M.; Guo, Y.J.P. Electric Field Enhances Shear Resistance of Polymer Melts via Orientational Polarization in Microstructures. Polymers 2020, 12, 335. [Google Scholar] [CrossRef] [Green Version]
- Im, D.J.; Noh, J.; Moon, D.; Kang, I.S. Electrophoresis of a charged droplet in a dielectric liquid for droplet actuation. Anal. Chem. 2011, 83, 5168–5174. [Google Scholar] [CrossRef]
- Lecuyer, S.; Ristenpart, W.; Vincent, O.; Stone, H. Electrohydrodynamic size stratification and flow separation of giant vesicles. Appl. Phys. Lett. 2008, 92, 104105. [Google Scholar] [CrossRef]
- Li, M.; Li, D. Vortices around Janus droplets under externally applied electrical field. Microfluid. Nanofluid. 2016, 20, 79. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, V.D.; Byun, D. Mechanism of electrohydrodynamic printing based on ac voltage without a nozzle electrode. Appl. Phys. Lett. 2009, 94, 173509. [Google Scholar] [CrossRef]
- Saville, D.A. Electrohydrodynamics: The Taylor-Melcher Leaky Dielectric Model. Annu. Rev. Fluid Mech. 1997, 29, 27–64. [Google Scholar] [CrossRef]
- Schnitzer, O.; Yariv, E. The Taylor–Melcher leaky dielectric model as a macroscale electrokinetic description. J. Fluid Mech. 2015, 773, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Bazant, M.Z. Electrokinetics meets electrohydrodynamics. J. Fluid Mech. 2015, 782, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; Young, Y.N. From electrodiffusion theory to the electrohydrodynamics of leaky dielectrics through the weak electrolyte limit. J. Fluid Mech. 2018, 855, 67–130. [Google Scholar] [CrossRef] [Green Version]
- Tomar, G.; Gerlach, D.; Biswas, G.; Alleborn, N.; Sharma, A.; Durst, F.; Welch, S.W.J.; Delgado, A. Two-phase electrohydrodynamic simulations using a volume-of-fluid approach. J. Comput. Phys. 2007, 227, 1267–1285. [Google Scholar] [CrossRef]
- Emdadi, M.; Pournaderi, P. Numerical simulation of conducting droplet impact on a surface under an electric field. Acta Mech. 2020, 231, 1083–1103. [Google Scholar] [CrossRef]
- Lac, E.; Homsy, G. Axisymmetric deformation and stability of a viscous drop in a steady electric field. J. Fluid Mech. 2007, 590, 239–264. [Google Scholar] [CrossRef]
- Lanauze, J.A.; Walker, L.M.; Khair, A.S. Nonlinear electrohydrodynamics of slightly deformed oblate drops. J. Fluid Mech. 2015, 774, 245–266. [Google Scholar] [CrossRef]
- Sherwood, J. Breakup of fluid droplets in electric and magnetic fields. J. Fluid Mech. 1988, 188, 133–146. [Google Scholar] [CrossRef] [Green Version]
- Fernández, A.; Tryggvason, G.; Che, J.; Ceccio, S.L. The effects of electrostatic forces on the distribution of drops in a channel flow: Two-dimensional oblate drops. Phys. Fluids 2005, 17, 093302. [Google Scholar] [CrossRef]
- Haywood, R.; Renksizbulut, M.; Raithby, G. Transient deformation of freely-suspended liquid droplets in electrostatic fields. AIChE J. 1991, 37, 1305–1317. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G. A conservative level set method for two phase flow. J. Comput. Phys. 2005, 210, 225–246. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G.; Zahedi, S. A conservative level set method for two phase flow II. J. Comput. Phys. 2007, 225, 785–807. [Google Scholar] [CrossRef]
- Paknemat, H.; Pishevar, A.; Pournaderi, P. Numerical simulation of drop deformations and breakup modes caused by direct current electric fields. Phys. Fluids 2012, 24, 102101. [Google Scholar] [CrossRef]
- Soni, P.; Juvekar, V.A.; Naik, V.M. Investigation on dynamics of double emulsion droplet in a uniform electric field. J. Electrost. 2013, 71, 471–477. [Google Scholar] [CrossRef]
- Jiang, Z.; Gan, Y.; Luo, Y. Effect of viscosity ratio on the dynamic response of droplet deformation under a steady electric field. Phys. Fluids 2020, 32, 053301. [Google Scholar]
- Huang, X.; He, L.; Luo, X.; Yin, H.; Yang, D. Deformation and coalescence of water droplets in viscous fluid under a direct current electric field. Int. J. Multiphas. Flow 2019, 118, 1–9. [Google Scholar] [CrossRef]
- Huang, X.; He, L.; Luo, X.; Yin, H. Droplet dynamic response in low-viscosity fluid subjected to a pulsed electric field and an alternating electric field. AIChE J. 2020, 66, e16869. [Google Scholar] [CrossRef]
- Ha, J.-W.; Yang, S.-M. Effect of nonionic surfactant on the deformation and breakup of a drop in an electric field. J. Colloid Interface Sci. 1998, 206, 195–204. [Google Scholar] [CrossRef]
- Ha, J.-W.; Yang, S.-M. Effects of surfactant on the deformation and stability of a drop in a viscous fluid in an electric field. J. Colloid Interface Sci. 1995, 175, 369–385. [Google Scholar] [CrossRef]
- Gu, Y.; Li, D. Electric charge on small silicone oil droplets dispersed in ionic surfactant solutions. J. Colloids Surf. A Physicochem. Eng. Asp. 1998, 139, 213–225. [Google Scholar] [CrossRef]
- Edwards, M.; Wu, X.; Wu, J.-S.; Huang, J.; H, K. Electric-field effects on a droplet microemulsion. Phys. Rev. E 1998, 57, 797. [Google Scholar] [CrossRef]
- Mousavichoubeh, M.; Shariaty-Niassar, M.; Ghadiri, M. The effect of interfacial tension on secondary drop formation in electro-coalescence of water droplets in oil. Chem. Eng. Sci. 2011, 66, 5330–5337. [Google Scholar] [CrossRef]
- Thiam, A.R.; Bremond, N.; Bibette, J. Adhesive emulsion bilayers under an electric field: From unzipping to fusion. Phys. Rev. Lett. 2011, 107, 068301. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-H.; Nguyen, X.H.; Ko, H.S. Study on droplet formation with surface tension for electrohydrodynamic inkjet nozzle. J. Mech. Sci. Technol. 2012, 26, 1403–1408. [Google Scholar] [CrossRef]
- Nganguia, H.; Young, Y.-N.; Vlahovska, P.M.; Blawzdziewicz, J.; Zhang, J.; Lin, H. Equilibrium electro-deformation of a surfactant-laden viscous drop. Phys. Fluids 2013, 25, 092106. [Google Scholar] [CrossRef] [Green Version]
- Wuzhang, J.; Song, Y.; Sun, R.; Pan, X.; Li, D. Electrophoretic mobility of oil droplets in electrolyte and surfactant solutions. Electrophoresis 2015, 36, 2489–2497. [Google Scholar] [CrossRef]
- He, L.; Yan, H.; Luo, X.; Wang, J.; Huang, X.; Cao, J.; Yang, D. An experimental investigation on the deformation of alkali-surfactant-polymer droplet under AC electric field. Colloid Polym. Sci. 2016, 294, 1651–1658. [Google Scholar] [CrossRef]
- Tuček, J.; Beránek, P.; Vobecká, L.; Slouka, Z.; Přibyl, M. Electric field driven addressing of oil-in-water droplets in the presence of gradients of ionic and nonionic surfactants. IEEE Trans. Ind. Appl. 2016, 52, 4337–4344. [Google Scholar] [CrossRef]
- Mandal, S.; Bandopadhyay, A.; Chakraborty, S. Dielectrophoresis of a surfactant-laden viscous drop. Phys. Fluids 2016, 28, 062006. [Google Scholar] [CrossRef]
- Luo, X.; Huang, X.; Yan, H.; Yang, D.; Wang, J.; He, L. Breakup modes and criterion of droplet with surfactant under direct current electric field. Chem. Eng. Res. Des. Stud. 2018, 132, 822–830. [Google Scholar] [CrossRef]
- Ervik, Å.; Penne, T.E.; Hellesø, S.M.; Munkejord, S.T.; Müller, B. Influence of surfactants on the electrohydrodynamic stretching of water drops in oil. Int. J. Multiphas. Flow 2018, 98, 96–109. [Google Scholar] [CrossRef] [Green Version]
- Poddar, A.; Mandal, S.; Bandopadhyay, A.; Chakrabort, S. Sedimentation of a surfactant-laden drop under the influence of an electric field. arXiv 2018, arXiv:1801.06317. [Google Scholar] [CrossRef] [Green Version]
- Sorgentone, C.; Tornberg, A.-K.; Vlahovska, P.M. A 3D boundary integral method for the electrohydrodynamics of surfactant-covered drops. J. Comput. Phys. 2019, 389, 111–127. [Google Scholar] [CrossRef] [Green Version]
- Poddar, A.; Mandal, S.; Bandopadhyay, A.; Chakraborty, S. Electrorheology of a dilute emulsion of surfactant-covered drops. J. Fluid Mech. 2019, 881, 524–550. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, K.; Ho, C.; Fong, W.; Toji, D. Properties of palm oil-in-water emulsions stabilized by nonionic emulsifiers. J. Colloid Interface Sci. 1996, 181, 595–604. [Google Scholar] [CrossRef]
- Mandal, S.; Ghosh, U.; Chakraborty, S. Effect of surfactant on motion and deformation of compound droplets in arbitrary unbounded Stokes flows. J. Fluid Mech. 2016, 803, 200–249. [Google Scholar] [CrossRef]
- Das, D.; Saintillan, D. Electrohydrodynamics of viscous drops in strong electric fields: Numerical simulations. J. Fluid Mech. 2017, 829, 127–152. [Google Scholar] [CrossRef] [Green Version]
- Ouriemi, M.; Vlahovska, P.M. Electrohydrodynamics of particle-covered drops. J. Fluid Mech. 2014, 751, 106–120. [Google Scholar] [CrossRef]
- Dommersnes, P.; Mikkelsen, A.; Fossum, J.O. Electro-hydrodynamic propulsion of counter-rotating Pickering drops. Eur. Phys. J. Spec. Top. 2016, 225, 699–706. [Google Scholar] [CrossRef] [Green Version]
- Behjatian, A.; Esmaeeli, A. Transient electrohydrodynamics of compound drops. Acta Mech. 2015, 226, 2581. [Google Scholar] [CrossRef]
- Schoeler, A.M.; Josephides, D.N.; Chaurasia, A.S.; Sajjadi, S.; Mesquida, P. Electrophoretic manipulation of multiple-emulsion droplets. Appl. Phys. Lett. 2014, 104. [Google Scholar] [CrossRef] [Green Version]
- Soni, P.; Dixit, D.; Juvekar, V.A. Effect of conducting core on the dynamics of a compound drop in an AC electric field. Phys. Fluids 2017, 29, 112108. [Google Scholar] [CrossRef]
- O’Konski, C.T.; Thacher, H.C., Jr. The distortion of aerosol droplets by an electric field. J. Phys. Chem. 1953, 57, 955–958. [Google Scholar] [CrossRef]
- Allan, R.; Mason, S. Particle behaviour in shear and electric fields II. Rigid rods and spherical doublets. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 267, 62–76. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Stratton, J.A. Electromagnetic Theory; John Wiley & Sons: Hoboken, NJ, USA, 2007; Volume 33. [Google Scholar]
- Lamb, H.J.P. Hydrodynamics; Cambridge University Press: Cambridge, UK, 1932; pp. 134–139. [Google Scholar]
- Esmaeeli, A.; Halim, M.A. Electrohydrodynamics of a liquid drop in AC electric fields. Acta Mech. 2018, 229, 3943–3962. [Google Scholar] [CrossRef]
- Dubash, N.; Mestel, A. Behaviour of a conducting drop in a highly viscous fluid subject to an electric field. J. Fluid Mech. 2007, 581, 469–493. [Google Scholar] [CrossRef]
- Lanauze, J.A.; Walker, L.M.; Khair, A.S. The influence of inertia and charge relaxation on electrohydrodynamic drop deformation. Phys. Fluids 2013, 25, 112101. [Google Scholar] [CrossRef]
- Nganguia, H.; Young, Y.-N.; Layton, A.; Lai, M.-C.; Hu, W.-F. Electrohydrodynamics of a viscous drop with inertia. Phys. Rev. E 2016, 93, 053114. [Google Scholar] [CrossRef] [Green Version]
- Vizika, O.; Saville, D.A. The electrohydrodynamic deformation of drops suspended in liquids in steady and oscillatory electric fields. J. Fluid Mech. 1992, 239, 1–21. [Google Scholar] [CrossRef]
- Jalaal, M.; Khorshidi, B.; Esmaeilzadeh, E. An experimental study on the motion, deformation and electrical charging of water drops falling in oil in the presence of high voltage D.C. electric field. Exp. Therm. Fluid Sci. 2010, 34, 1498–1506. [Google Scholar] [CrossRef]
- Mandal, S.; Chakrabarti, S.; Chakraborty, S. Effect of nonuniform electric field on the electrohydrodynamic motion of a drop in Poiseuille flow. Phys. Fluids 2017, 29, 052006. [Google Scholar] [CrossRef]
- Mandal, S.; Sinha, S.; Bandopadhyay, A.; Chakraborty, S. Drop deformation and emulsion rheology under the combined influence of uniform electric field and linear flow. J. Fluid Mech. 2018, 841, 408–433. [Google Scholar] [CrossRef]
- Esmaeeli, A.; Behjatian, A. Transient electrohydrodynamics of a liquid drop at finite Reynolds numbers. J. Fluid Mech. 2020, 893, 26. [Google Scholar] [CrossRef]
- Berg, G.; Lundgaard, L.E.; Abi-Chebel, N. Electrically stressed water drops in oil. Chem. Eng. Process. Process Intensif. 2010, 49, 1229–1240. [Google Scholar] [CrossRef]
- Gong, H.; Peng, Y.; Yang, Z.; Shang, H.; Zhang, X. Stable deformation of droplets surface subjected to a high-voltage electric field in oil. Colloids Surf. A Physicochem. Eng. Asp. 2015, 468, 315–321. [Google Scholar] [CrossRef]
- Esmaeeli, A. Transient electrohydrodynamics of a liquid drop in AC electric fields. Eur. Phys. J. E 2018, 41, 135. [Google Scholar] [CrossRef] [PubMed]
- Collins, R.T.; Sambath, K.; Harris, M.T.; Basaran, O.A. Universal scaling laws for the disintegration of electrified drops. Proc. Natl. Acad. Sci. USA 2013, 110, 4905. [Google Scholar] [CrossRef] [Green Version]
- Gawande, N.; Mayya, Y.; Thaokar, R. Jet and progeny formation in the Rayleigh breakup of a charged viscous drop. J. Fluid Mech. 2020. [Google Scholar] [CrossRef]
- Sengupta, R.; Walker, L.M.; Khair, A.S. The role of surface charge convection in the electrohydrodynamics and breakup of prolate drops. J. Fluid Mech. 2017, 833, 29–53. [Google Scholar] [CrossRef]
- Ha, J.-W.; Yang, S.-M. Electrohydrodynamics and electrorotation of a drop with fluid less conductive than that of the ambient fluid. Phys. Fluids 2000, 12, 764–772. [Google Scholar] [CrossRef] [Green Version]
- Salipante, P.F.; Vlahovska, P.M. Electrohydrodynamics of drops in strong uniform dc electric fields. Phys. Fluids 2010, 22, 112110. [Google Scholar] [CrossRef]
- Salipante, P.F.; Vlahovska, P.M. Electrohydrodynamic rotations of a viscous droplet. Phys. Rev. E 2013, 88, 043003. [Google Scholar] [CrossRef] [Green Version]
- Vlahovska, P.M. Electrohydrodynamic instabilities of viscous drops. Phys. Rev. Fluids 2016, 1, 060504. [Google Scholar] [CrossRef]
- Masliyah, J.H.; Bhattacharjee, S. Electrokinetic and Colloid Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Abbasi, M.S.; Farooq, H.; Ali, H.; Kazim, A.H.; Nazir, R.; Shabbir, A.; Cho, S.; Song, R.; Lee, J. Deformation of Emulsion Droplet with Clean and Particle-Covered Interface under an Electric Field. Materials 2020, 13, 2984. [Google Scholar] [CrossRef]
- Ouriemi, M.; Vlahovska, P.M. Electrohydrodynamic Deformation and Rotation of a Particle-Coated Drop. Langmuir 2015, 31, 6298–6305. [Google Scholar] [CrossRef] [Green Version]
- Ha, J.-W.; Yang, S.-M. Electrohydrodynamic effects on the deformation and orientation of a liquid capsule in a linear flow. Phys. Fluids 2000, 12, 1671–1684. [Google Scholar] [CrossRef] [Green Version]
- Nudurupati, S.; Janjua, M.; Aubry, N.; Singh, P.J.E. Concentrating particles on drop surfaces using external electric fields. Electrophoresis 2008, 29, 1164–1172. [Google Scholar] [CrossRef]
- Nudurupati, S.; Janjua, M.; Singh, P.; Aubry, N. Effect of parameters on redistribution and removal of particles from drop surfaces. Soft Matter 2010, 6, 1157–1169. [Google Scholar] [CrossRef]
- Hwang, K.; Singh, P.; Aubry, N. Destabilization of Pickering emulsions using external electric fields. Electrophoresis 2010, 31, 850–859. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Tan, P.; Chen, S.; Huang, J.; Wen, W.; Xu, L. Coalescence of pickering emulsion droplets induced by an electric field. Phys. Rev. Lett. 2013, 110, 064502. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, M.; Emrick, T.; Russell, T.P. Stabilizing liquid drops in nonequilibrium shapes by the interfacial jamming of nanoparticles. Science 2013, 342, 460–463. [Google Scholar] [CrossRef]
- Rozynek, Z.; Dommersnes, P.; Mikkelsen, A.; Michels, L.; Fossum, J. Electrohydrodynamic controlled assembly and fracturing of thin colloidal particle films confined at drop interfaces. Eur. Phys. J. Spec. Top. 2014, 223, 1859–1867. [Google Scholar] [CrossRef]
- Rozynek, Z.; Mikkelsen, A.; Dommersnes, P.; Fossum, J.O. Electroformation of Janus and patchy capsules. Nat. Commun. 2014, 5, 3945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rozynek, Z.; Castberg, R.; Kalicka, A.; Jankowski, P.; Garstecki, P. Electric field manipulation of particles in leaky dielectric liquids. Arch. Mech. 2015, 67, 385–399. [Google Scholar]
- Dommersnes, P.; Fossum, J. Surface structuring of particle laden drops using electric fields. Eur. Phys. J. Spec. Top. 2016, 225, 715–728. [Google Scholar] [CrossRef]
- Mikkelsen, A.; Rozynek, Z.; Khobaib, K.; Dommersnes, P.; Fossum, J.O. Transient deformation dynamics of particle laden droplets in electric field. Colloids Surf. A Physicochem. Eng. Asp. 2017, 532, 252–256. [Google Scholar] [CrossRef]
- Mikkelsen, A.; Khobaib, K.; Eriksen, F.K.; Måløy, K.J.; Rozynek, Z. Particle-covered drops in electric fields: Drop deformation and surface particle organization. Soft Matter 2018, 14, 5442–5451. [Google Scholar] [CrossRef] [Green Version]
- Amah, E.; Shah, K.; Fischer, I.; Singh, P. Electrohydrodynamic manipulation of particles adsorbed on the surface of a drop. Soft Matter 2016, 12, 1663–1673. [Google Scholar] [CrossRef]
- Teigen, K.E.; Song, P.; Lowengrub, J.; Voigt, A. A diffuse-interface method for two-phase flows with soluble surfactants. J. Comput. Phys. 2011, 230, 375–393. [Google Scholar] [CrossRef] [Green Version]
- Yeh, C.-H.; Lee, M.-H.; Lin, Y.-C. Using an electro-spraying microfluidic chip to produce uniform emulsions under a direct-current electric field. Microfluid. Nanofluid. 2012, 12, 475–484. [Google Scholar] [CrossRef] [Green Version]
- Renardy, Y.Y.; Renardy, M.; Cristini, V. A new volume-of-fluid formulation for surfactants and simulations of drop deformation under shear at a low viscosity ratio. Eur. J. Mech. B Fluids 2002, 21, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Ervik, Å.; Hellesø, S.M.; Munkejord, S.T.; Müller, B. Experimental and Computational Studies of Water Drops Falling through Model Oil with Surfactant and Subjected to an Electric Field. In Proceedings of the 18th IEEE International Conference on Dielectric Liquids (ICDL), Bled, Slovenia, 29 June–3 July 2014; pp. 1–6. [Google Scholar]
- Teigen, K.E.; Munkejord, S.T. Sharp-interface simulations of drop deformation in electric fields. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 475–482. [Google Scholar] [CrossRef]
- Enayati, M.; Ahmad, Z.; Stride, E.; Edirisinghe, M. One-step electrohydrodynamic production of drug-loaded micro- and nanoparticles. J. R. Soc. Interface 2010, 7, 667–675. [Google Scholar] [CrossRef] [Green Version]
- Enayati, M.; Chang, M.-W.; Bragman, F.; Edirisinghe, M.; Stride, E.J.C. Electrohydrodynamic preparation of particles, capsules and bubbles for biomedical engineering applications. Colloids Surf. A Physicochem. Eng. Asp. 2011, 382, 154–164. [Google Scholar] [CrossRef]
- Behjatian, A.; Esmaeeli, A. Electrohydrodynamics of a compound drop. Phys. Rev. E 2013, 88, 033012. [Google Scholar] [CrossRef]
- Soni, P.; Thaokar, R.M.; Juvekar, V.A. Electrohydrodynamics of a concentric compound drop in an AC electric field. Phys. Fluids 2018, 30, 032102. [Google Scholar] [CrossRef] [Green Version]
- Gouz, H.N.; Sadhal, S.S. Fluid dynamics and stability analysis of a compound droplet in an electric field. Q. J. Mech. Appl. Math. 1989, 42, 65–83. [Google Scholar] [CrossRef]
- Ha, J.-W.; Yang, S.-M. Fluid dynamics of a double emulsion droplet in an electric field. Phys. Fluids 1999, 11, 1029–1041. [Google Scholar] [CrossRef] [Green Version]
- Tsukada, T.; Mayama, J.; Sato, M.; Hozawa, M. Theoretical and Experimental Studies on the Behavior of a Compound Drop under a Uniform DC Electric Field. J. Chem. Eng. Jpn. 1997, 30, 215–222. [Google Scholar] [CrossRef] [Green Version]
- Bei, Z.; Jones, T.B.; Harding, D.R. Electric field centering of double-emulsion droplets suspended in a density gradient. Soft Matter 2010, 6, 2312–2320. [Google Scholar] [CrossRef]
- Bei, Z.-M.; Jones, T.; Tucker-Schwartz, A.; Harding, D. Electric field mediated droplet centering. Appl. Phys. Lett. 2008, 93, 184101. [Google Scholar] [CrossRef] [Green Version]
- Bei, Z.-M.; Jones, T.; Tucker-Schwartz, A. Forming concentric double-emulsion droplets using electric fields. J. Electrost. 2009, 67, 173–177. [Google Scholar] [CrossRef]
- Santra, S.; Das, S.; Chakraborty, S. Electrically modulated dynamics of a compound droplet in a confined microfluidic environment. J. Fluid Mech. 2020, 882. [Google Scholar] [CrossRef]
- Santra, S.; Das, S.; Chakraborty, S. Electric field-induced pinch-off of a compound droplet in Poiseuille flow. Phys. Fluids 2019, 31, 062004. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.H.; Men, Y.F.; Senapati, S.; Chang, H.C. Immersed AC electrospray (iACE) for monodispersed aqueous droplet generation. Biomicrofluidics 2018, 12, 044113. [Google Scholar] [CrossRef]
- Yin, S.; Huang, Y.; Wong, T.N.; Chong, W.H.; Ooi, K.T. Electric Scissors for Precise Generation of Organic Droplets in Microfluidics: A Universal Approach that Goes beyond Surface Wettability. J. Phys. Chem. C 2019, 123, 25643–25650. [Google Scholar] [CrossRef]
- Azizian, P.; Azarmanesh, M.; Dejam, M.; Mohammadi, M.; Shamsi, M.; Sanati-Nezhad, A.; Mohamad, A.A. Electrohydrodynamic formation of single and double emulsions for low interfacial tension multiphase systems within microfluidics. Chem. Eng. Sci. 2019, 195, 201–207. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, Z.; Liu, Y.X.; Shao, C.M.; Bian, F.K.; Zhao, Y.J. Biomimetic enzyme cascade reaction system in microfluidic electrospray microcapsules. Sci. Adv. 2018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, D.; Yu, Y.R.; Zhao, C.; Shou, X.; Piao, Y.; Zhao, X.; Zhao, Y.J.; Wang, S.Q. NK-Cell-Encapsulated Porous Microspheres via Microfluidic Electrospray for Tumor Immunotherapy. ACS Appl. Mater. Interfaces 2019, 11, 33716–33724. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.B.; Wang, J.F.; Yongphet, P.; Wang, X.Y.; Zuo, Z.W.; Li, B.; Zhang, W. Experimental study on electric-field-induced droplet generation and breakup in an immiscible medium. Exp. Fluids 2020, 61, 1–12. [Google Scholar] [CrossRef]
- Lee, K.H.; Yang, G.L.Z.; Wyslouzil, B.E.; Winter, J.O. Electrohydrodynamic Mixing-Mediated Nanoprecipitation for Polymer Nanoparticle Synthesis. ACS Appl. Polym. Mater. 2019, 1, 691–700. [Google Scholar] [CrossRef]
- Su, Y.; Yu, T.; Wang, G.; Zhang, C.; Liu, Z. Numerical simulation of electrohydrodynamics of a compound drop based on the ternary phase field method. Sci. Prog. 2019. [Google Scholar] [CrossRef]
- Lee, S.J.; Kang, J.Y.; Choi, W.; Kwak, R. Simultaneous electric production and sizing of emulsion droplets in microfluidics. Soft Matter 2020, 16, 614–622. [Google Scholar] [CrossRef]
- Rozynek, Z.; Khobaib, K.; Mikkelsen, A. Opening and Closing of Particle Shells on Droplets via Electric Fields and Its Applications. ACS Appl. Mater. Interfaces 2019, 11, 22840–22850. [Google Scholar] [CrossRef]
- Li, M.Q.; Li, D.Q. Redistribution of charged aluminum nanoparticles on oil droplets in water in response to applied electrical field. J. Nanoparticle Res. 2016. [Google Scholar] [CrossRef] [Green Version]
- Brosseau, Q.; Hickey, G.; Vlahovska, P.M. Electrohydrodynamic Quincke rotation of a prolate ellipsoid. Phys. Rev. Fluids 2017. [Google Scholar] [CrossRef]
- Pradillo, G.E.; Karani, H.; Vlahovska, P.M. Quincke rotor dynamics in confinement: Rolling and hovering. Soft Matter 2019, 15, 6564–6570. [Google Scholar] [CrossRef] [PubMed]
- Jákli, A.; Senyuk, B.; Liao, G.; Lavrentovich, O.D. Colloidal micromotor in smectic A liquid crystal driven by DC electric field. Soft Matter 2008, 4, 2471–2474. [Google Scholar] [CrossRef]
- Das, D.; Lauga, E. Active Particles Powered by Quincke Rotation in a Bulk Fluid. Phys. Rev. Lett. 2019, 122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zrinyi, M.; Nakano, M. Toward Colloidal Motors. Period. Polytech.-Chem. Eng. 2017, 61, 15–18. [Google Scholar] [CrossRef] [Green Version]
- Belovs, M.; Cebers, A. Quincke rotation driven flows. Phys. Rev. Fluids 2020. [Google Scholar] [CrossRef]
- Nudurupati, S.; Janjua, M.; Singh, P.; Aubry, N. Electrohydrodynamic removal of particles from drop surfaces. Phys. Rev. E 2009. [Google Scholar] [CrossRef]
- Rozynek, Z.; Jozefczak, A. Patchy colloidosomes—An emerging class of structures. Eur. Phys. J. Spec. Top. 2016, 225, 741–756. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.K.; Ren, Y.; Hou, L.K.; Liu, W.Y.; Jiang, T.Y.; Deng, X.K.; Tao, Y.; Jiang, H.Y. Electrically controlled rapid release of actives encapsulated in double-emulsion droplets. Lab Chip 2018, 18, 1121–1129. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.K.; Ren, Y.K.; Hou, L.K.; Liu, W.Y.; Jiang, T.Y.; Jiang, H.Y. Compound-Droplet-Pairs-Filled Hydrogel Microfiber for Electric-Field-Induced Selective Release. Small 2019. [Google Scholar] [CrossRef]











| Ref. | Approach a | Method b,c | Deformation Type | Characteristics | Remarks | |
|---|---|---|---|---|---|---|
| Single-phase droplet (clean) | ||||||
| [1] | E and A | Leaky-dielectric model, o/o emulsion (S/C and C/S), | Both | Deformation | DC field | |
| [7] | E and A | Leaky-dielectric model, o/o emulsion (S/C, C/S, etc.) w/o emulsion (W/C, W/S, etc.) | Both | Deformation, pinch-off, dimpling | DC and AC field | |
| [18] | E and A | Leaky-dielectric model, o/o emulsion (S/C),electrolyte (AOT, TBAB), linear stability analysis | Oblate (R/S > 1) | Streaming from equator, Quincke rotation, dimpling | DC field, micro-droplet generation | |
| [24] | E | Leaky-dielectric model, w/o emulsion (W/S, G/S, etc.), o/o emulsion (C/S), non-Newtonian emulsion (PAM and XAN solution) | Prolate (R/S < 1) | Deformation, pinch-off, tip streaming | DC field, effect of viscosity | |
| [90] | A and N | Leaky-dielectric model, boundary element method, interfacial charge convection | Oblate (R/S > 1) | Deformation, Quincke rotation | DC field, 3D simulation | |
| Single-phase droplet (surfactant-laden) | ||||||
| [72] | E and A | Leaky-dielectric model, linear stability analysis, o/o emulsion (PVDF/PS, S/C, C/S), w/o emulsion (W/S), surfactant (PS-b-PMMA, Tween 60, etc.), non-Newtonian fluid (XAN solution) | Both | Deformation, bulbous end, tip streaming | DC field, effect of viscosity, non-ionic surfactant | |
| [84] | E and N | Level-set method, ghost-fluid method, w/o emulsion (W/Marcol 52), surfactant (Span 80) | < 0.3 | Prolate (R/S < 1) | Deformation, breakup | DC field, non-ionic surfactant |
| Single-phase droplet (particle-covered) | ||||||
| [91] | E and A | Leaky-dielectric model, o/o emulsion (S/C), particle (Al, glass, PMMA, PE, etc.) | Oblate (R/S > 1) | Deformation, Quincke rotation | DC field, particle self-assembly | |
| [92] | E and A | Leaky-dielectric model, o/o emulsion (S/C), particle (PE) | 1 < < 8 | Oblate (R/S > 1) | Quincke rotation | DC field, micro-motor |
| Multi-phase droplet (clean) | ||||||
| [13] | E, A, and N | Leaky dielectric model, level-set method, o/o/o emulsion (C/S/C), electrolyte (Red-O dye) | Prolate/Oblate | Deformation, pinch-off, bulbous end, tip streaming | DC field, effect of viscosity, and R/S | |
| [93] | A | Leaky-dielectric model, closed form analytical solution, o/o/o emulsion (C/S/C, C/Corn/S, S/C/S, etc.) | < 0.1 | Both/Both | Deformation | DC field |
| [94] | E | o/w/o emulsion (S/W/S), w/o/w/o emulsion (W/S/W/S), | < 0.1 | Oblate/Prolate, P/O/P | Eccentricity stability, electro-phoresis | DC field |
| [95] | E and N | Leaky dielectric model, phase field model, w/o/o emulsion (W/C/S) | Prolate/Prolate | Deformation, pinch-off, tip streaming | AC field | |
| Multi-phase droplet (surfactant-laden) | ||||||
| [16] | E and A | Leaky dielectric model, w/o/o emulsion (W/S/C), surfactant (Tween 80) | Prolate/Oblate | Deformation, bulbous end | DC field | |
| [25] | E and A | Leaky dielectric model, o/w/o emulsion (HC/WE/S), w/o/o emulsion (WE/C/S), surfactant (Span85, Brij58) | Both/Oblate | Pinch-off, tip streaming | DC field, multi-core double emulsion | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abbasi, M.S.; Song, R.; Cho, S.; Lee, J. Electro-Hydrodynamics of Emulsion Droplets: Physical Insights to Applications. Micromachines 2020, 11, 942. https://doi.org/10.3390/mi11100942
Abbasi MS, Song R, Cho S, Lee J. Electro-Hydrodynamics of Emulsion Droplets: Physical Insights to Applications. Micromachines. 2020; 11(10):942. https://doi.org/10.3390/mi11100942
Chicago/Turabian StyleAbbasi, Muhammad Salman, Ryungeun Song, Seongsu Cho, and Jinkee Lee. 2020. "Electro-Hydrodynamics of Emulsion Droplets: Physical Insights to Applications" Micromachines 11, no. 10: 942. https://doi.org/10.3390/mi11100942
APA StyleAbbasi, M. S., Song, R., Cho, S., & Lee, J. (2020). Electro-Hydrodynamics of Emulsion Droplets: Physical Insights to Applications. Micromachines, 11(10), 942. https://doi.org/10.3390/mi11100942