Mobility Models Based on Forward Current-Voltage Characteristics of P-type Pseudo-Vertical Diamond Schottky Barrier Diodes

Abstract

Compared with silicon and silicon carbide, diamond has superior material parameters and is therefore suitable for power switching devices. Numerical simulation is important for predicting the electric characteristics of diamond devices before fabrication. Here, we present numerical simulations of p-type diamond pseudo-vertical Schottky barrier diodes using various mobility models. The constant mobility model, based on the parameter μ_const, fixed the hole mobility absolutely. The analytic mobility model resulted in temperature- and doping concentration-dependent mobility. An improved model, the Lombard concentration, voltage, and temperature (CVT) mobility model, considered electric field-dependent mobility in addition to temperature and doping concentration. The forward voltage drop at 100 A/cm² using the analytic and Lombard CVT mobility models was 2.86 and 5.17 V at 300 K, respectively. Finally, we used an empirical mobility model based on experimental results from the literature. We also compared the forward voltage drop and breakdown voltage of the devices, according to variations in p- drift layer thickness and cathode length. The device successfully achieved a low specific on-resistance of 6.8 mΩ∙cm², a high breakdown voltage of 1190 V, and a high figure-of-merit of 210 MW/cm².

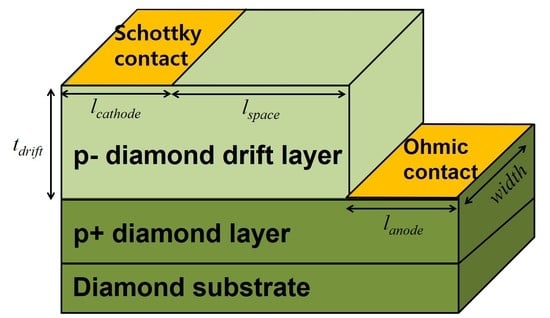
1. Introduction

Diamond is a promising semiconductor for power switches due to its wide band gap, high critical field, and high thermal conductivity [1,2,3]. Diamond has a wide band gap of 5.5 eV, which corresponds to the boundary between semiconductors and insulators. Diamond’s high breakdown field (> 10 MV/cm) enables a thin drift layer and low on-resistance in power devices. Its thermal conductivity is 22 W/cm/K, which is the highest of any material on earth. Diamond could replace Si and SiC in conventional power devices, especially for high-temperature and high-power applications [4,5,6,7,8,9,10,11].

The ionization energies of phosphorous for n-type diamond and boron for p-type diamond are 570 and 370 meV at room temperature, respectively [12]. When boron concentration increases, the ionization energy decreases due to the change in carrier transport properties from band transport to hopping conduction [12,13]. Operating diamond power devices at elevated temperatures can also increase the number of ionized carriers [14]. Technologies for growing and processing diamond are still in development. A pseudo-vertical diode enabled a local vertical current flow, which was useful considering the level of technology at that time. A pseudo-vertical diamond diode that enabled local vertical current flow was demonstrated; the diode had a 14 μm-thick p-layer, was fabricated using an etching process, and exhibited a high breakdown voltage of 1.6 kV and low leakage current of 10⁻⁷–10⁻⁶ A/cm² [15]. The electrical characteristics of this device were recorded using a field plate on an Al₂O₃ dielectric layer [16]. A diamond device with high dislocation density was found to exhibit a high leakage current, as shown using a defect visualization technique [17], while a diamond PIN diode with a 8.5-μm-thick intrinsic layer on IIa-type (100) bulk substrate was found to have an experimental breakdown voltage of 1040 V [18].

Simulations and numerical models can be used to forecast the electrical characteristics of devices before fabrication. Such experimental approaches are important; however, a simulation technology for diamond still needs to be developed. Basic parameters and models for diamond devices have been discussed [19]; a simulation of junction termination structures in diamond Schottky barrier diodes (SBDs) was discussed in [20,21]; simulation models for diamond bipolar devices were analyzed and discussed in detail in [22]; and, three-dimensional simulations of depleted Schottky PIN diamond diodes were performed in [23]. A quantum simulation of a nitrogen-terminated diamond (111) surface has also been reported [24], and a diamond Schottky PIN and SBD have been simulated with breakdown voltages from 70 to 5000 V [4]. We previously reported the simulated breakdown voltage of p-type diamond pseudo-vertical SBDs with modified impact ionization coefficients [25].

In this paper, we focus on the forward current–voltage (I–V) characteristics of p-type pseudo-vertical diamond SBDs using mobility models. Identical devices were simulated using constant, analytic [26,27], Lombardi CVT (concentration, voltage, and temperature) [28], and empirical mobility models [22]; the empirical mobility model was based on Volpe’s experiment [29]. The mobility models yielded different forward I–V characteristics due to differences in the degree of dependence on temperature, doping concentration, and electric field. We chose the Atlas numerical simulation tool within the Silvaco software [30] to investigate the forward voltage drop (V_f), specific on-resistance (R_on,sp), and breakdown voltage of p-type pseudo-vertical diamond SBDs.

2. Numerical Methods

The device structure was designed in a sequence of defining mesh, region, electrode, doping, and contact. We defined various material parameters of the p-type diamond, choice models with physical equations, and selected numerical methods to solve the equations, and finally swept the voltage on the electrodes. Values of 5.5 eV, 1.5 eV, 5.7 × 10⁻⁹ s, and 5 × 10¹⁹ cm⁻³ were used for the energy band gap, affinity, permittivity, Shockley-Read-Hall hole lifetime, and room temperature density of states in the valence band, respectively [31]. Figure 1 shows the cross-sectional view and simulated energy band at the Schottky contact of the p-type diamond pseudo-vertical SBD. The voltage was not applied in the energy band at 300 K. The hole current flows vertically from the Schottky contact (cathode) to the interface between the p- drift layer and the p+ layer; then, it flows laterally through the interface to the Ohmic contact (anode). The Schottky contact was platinum, with a metal work function (ϕ_m) of 5.65 eV. The Schottky barrier height (ϕ_b) was 1.35 eV from the Mott equation and simulation, respectively. The doping concentration of the p- drift layer (N_a) was 10¹⁵ cm⁻³ for the high breakdown voltage. The N_a increased with increasing temperature, but this was not taken into account to focus on the mobility study with temperature. It is necessary to consider the limitation of the assumption. The thickness of the p- drift layer (t_drift) was 4.6 μm. The lateral length of the Schottky (l_cathode) and Ohmic contacts (l_anode) was 2 and 2 μm, respectively, and the spacing between Schottky and Ohmic contacts (l_space) was 16 μm.

The saturation velocity of holes was fixed at 2.7 × 10⁷ cm/s so that the forward current was determined by the hole mobility. The hole mobility in the p-type low-doped diamond was controlled by ionized impurity, acoustic phonon, and optical phonon scattering [32]. We considered four mobility models related to scattering, namely constant, analytic, Lombardi CVT, and empirical mobility models. We defined V_f at a current density of 100 A/cm². The current density was defined as current per width divided by the sum of l_cathode, l_space, and l_anode, and R_on,sp was extracted from the reciprocal of the I–V slope between the built-in potential and V_f.

3. Simulation Results and Discussion

3.1. Constant Mobility Model

The doping concentration of the p- drift layer and the saturation velocity of the holes were fixed, so that the hole mobility and forward current were affected by scattering. First, we investigated the device using the constant mobility model, which considers the mobility to be dependent only on acoustic phonon scattering due to temperature. We used Equation (1) for the constant mobility model. Here, μ_p, T, and μ_const are the hole mobility, lattice temperature, and constant mobility at 300 K, respectively. Equation (1) does not take into account any change in mobility due to the doping concentration or electric field.

$${\mu }_p\left(T\right)={\mu }_{const}{\left(\frac{T}{300}\right)}^{-1.5}$$

(1)

Figure 2 shows the forward I–V characteristics of the p-type diamond pseudo-vertical SBD simulated using the constant mobility model with various μ_const. The extracted V_f and R_on,sp is shown in

Table 1. Hole mobility, forward voltage drop (V_f), and specific on-resistance (R_on,sp) of the p-type diamond pseudo-vertical Schottky barrier diode (SBD) simulated using the constant mobility model with μ_const of 1000, 2000, 3000, and 4000 cm²/Vs. The lattice temperature was 300 K.

μconst (cm2/Vs)	Hole Mobility (cm2/Vs)	Forward Voltage Drop (V)	Specific on-Resistance (mΩ∙cm2)
1000	1000	2.47	14.1
2000	2000	1.76	7.0
3000	3000	1.52	4.6
4000	4000	1.40	3.4

. The anode voltage (V_a) was swept from −10 to 10 V at 300 K. The Schottky barrier height of the p-type SBD was defined by E_g − (ϕ_m − χ). Finally, the built-in potential was calculated as the difference between the Schottky barrier height and E_F − E_v, where E_F and E_v were derived from the Fermi energy level and edge of the valence band, respectively. The built-in potential was 1.1 V at 300 K. When μ_const was 1000, 2000, 3000, and 4000 cm²/Vs, V_f was 2.47, 1.76, 1.52, and 1.40 V at 300 K, respectively. These values can be converted to values of R_on,sp as 14.1, 7.0, 4.6, and 3.4 mΩ∙cm² at μ_const of 1000, 2000, 3000, and 4000 cm²/Vs, respectively. The typical mobility at the 10¹⁵ cm⁻³-doped p-drift layer was 1990 cm²/Vs from the empirical mobility model [29]. The value of μ_const is important for the constant mobility model.

For a value of μ_const of 2000 cm²/Vs, we simulated the forward I–V characteristics at 200, 300, 400, and 500 K. Figure 3 shows the simulated forward I–V characteristics of the p-type diamond pseudo-vertical SBD with a μ_const value of 2000 cm²/Vs at 200, 300, 400, and 500 K, respectively. The extracted built-in potential, hole mobility, V_f and R_on,sp are shown in

Table 2. Built-in potential, hole mobility, forward voltage drop (V_f) and specific on-resistance (R_on,sp) of the p-type diamond pseudo-vertical Schottky barrier diode (SBD) simulated using the constant, analytic, Lombardi CVT, and empirical mobility models. The constant mobility model used the μ_const of 2000 cm²/Vs.

Mobility Model	Temperature (K)	Built-in Potential (V)	Hole Mobility (cm2/Vs)	Forward Voltage Drop (V)	Specific on-Resistance (mΩ∙cm2)
Constant	200	1.2	3670	1.57	3.8
	300	1.1	2000	1.76	7.0
	400	1.0	1300	2.01	10.9
	500	0.8	930	2.30	14.8
Analytic	200	1.2	720	3.16	19.3
	300	1.1	790	2.86	17.5
	400	1.0	800	2.69	17.4
	500	0.8	790	2.57	17.5
Lombardi CVT	200	1.2	-	2.84	17.2
	300	1.1	-	5.17	40.8
	400	1.0	-	9.11	82.0
	500	0.8	-	15.49	145.8
Empirical	300	1.1	1990	1.77	6.8
	400	1.0	820	2.65	16.8
	500	0.8	410	4.20	33.7
Experimental [15]	300	2.1	-	-	18.5

. When the lattice temperature was 200, 300, 400, and 500 K and μ_const was 2000 cm²/Vs, the values of V_f were 1.57, 1.76, 2.01, and 2.30 V, respectively, and the values of R_on,sp were 3.8, 7.0, 10.9, and 14.8 mΩ∙cm², respectively. Low temperature increased the Schottky barrier height. However, the decrease in temperature also increased the hole mobility and forward current due to the reduced acoustic phonon scattering. Hole mobilities of 3670, 2000, 1300, and 930 cm²/Vs were measured at 200, 300, 400, and 500 K, respectively, with μ_const set at 2000 cm²/Vs. The constant mobility model has limitations because it only considers acoustic phonon scattering. In addition, N_a and V_a do not change the hole mobility in this model.

3.2. Analytic Mobility Model

The constant mobility model does not take the doping concentration or electric field into account. The hole mobility using the constant mobility model was identical under different doping concentrations. The analytic mobility model can calculate the doping concentration- and temperature-dependent mobility [26,27], and considers both acoustic phonon and ionized impurity scattering. Equation (2), below, was used for this model. The parameters of μ_min, m₁, C₀, γ₂, and n_min for diamond were obtained from the literature [33], and set at 55 cm²/Vs, −2, 1.12 × 10¹⁴ cm⁻³, 0.589, and 2.5, respectively. The values of μ_max and n_max were 4399 cm²/Vs and −3.4 at lattice temperatures between 343 and 600 K, and 3433 cm²/Vs and −1.55 at lattice temperatures below 343 K, respectively. Figure S1 in the Supplementary Material shows the forward I–V characteristics of the device using the analytic mobility model at 200, 300, 400, and 500 K. The extracted built-in potential, hole mobility, V_f and R_on,sp at various temperatures of the device using analytic mobility model are shown in Table 2. The values of V_f were 3.16, 2.86, 2.69, and 2.57 V at 200, 300, 400, and 500K, respectively. These values can be used to calculate values of R_on,sp of 19.3, 17.5, 17.4, and 17.5 mΩ∙cm² at 200, 300, 400, and 500 K, respectively. The built-in potential decreased with decreasing lattice temperature. The extracted hole mobility of the p- drift layer at 200 K was 720 cm²/Vs which was less than those at 300, 400, or 500 K, respectively, due to the ionized impurity scattering. In addition, the hole mobility in the analytic mobility model did not change with changes in the electric field.

$${\mu }_p\left(N_a,T\right)={\mu }_{min}{\left(\frac{T}{300}\right)}^{n_{min}}+\frac{{\mu }_{max}{\left(\frac{T}{300}\right)}^{n_{max}}- {\mu }_{min}{\left(\frac{T}{300}\right)}^{n_{min}}}{1+{\left(\frac{T}{300}\right)}^{m_1}{\left(\frac{N_a}{C_0}\right)}^{{\gamma }_2}}$$

(2)

3.3. Lombardi CVT Mobility Model

When V_a is applied, an electric field is distributed inside the p- drift layer. This distribution can vary the mobility in the p- drift layer. However, the analytic mobility model does not allow mobility variation in layers with the same doping concentrations. In contrast, the Lombardi CVT mobility model can account for such variations; for example, this model can take account of the mobility degradation in an inversion layer of metal-oxide-semiconductor field-effect transistors. The Lombardi CVT mobility model considers the perpendicular electric field, doping concentration, and temperature-dependent mobility [28]. Scattering with surface acoustic phonons, surface roughness, and optical intervalley phonons, denoted by μ_ac, μ_sr and μ_b, respectively, all limit the mobility. Important parameters for Lombardi CVT mobility are T, N_a, and the perpendicular electric field. The hole mobility was determined using Matthiessen’s rule:

$$\frac{1}{{\mu }_p}=\frac{1}{{\mu }_{ac}}+\frac{1}{{\mu }_{sr}}+\frac{1}{{\mu }_b}$$

(3)

Figure 4 shows the forward I–V characteristics of the p-type diamond pseudo-vertical SBD simulated using the analytic and Lombard CVT mobility models, respectively. The values of V_f using the analytic and Lombard CVT mobility models were 2.86 and 5.17 V at 300 K, respectively. The values of R_on,sp from the analytic and Lombard CVT mobility models were 17.5 and 40.8 mΩ∙cm² at 300 K, respectively. When the value of V_a increased up to 8 V, the forward currents with the analytic and Lombard CVT mobility models were 394 and 155 A/cm², respectively. When V_a increased, the forward current using the Lombardi CVT mobility model decreased compared with that using the analytic mobility model, because the Lombardi CVT mobility model considers the decrease in mobility caused by the high electric field (in particular, the electric field concentrated on the right edge of the Schottky contact that resulted in the low mobility).

Figure 5 and Figure 6 show the hole mobility of the p-type diamond pseudo-vertical SBD simulated using the analytic and Lombard CVT mobility models at a V_a of 2 V, respectively. The analytic mobility fixes the hole mobility even if the potential or electric field is varied. However, the Lombardi CVT mobility model changes the hole mobility in response to the two-dimensional distribution of the potential and electric field. We also extracted the hole mobility across section A-A’ from Figure 5 and Figure 6, as shown in Figure 7. The hole mobility with the analytic model did not change due to the electric field. The scattering of the Lombardi CVT mobility model reduced the hole mobility. In addition, the electric field was concentrated at the edge of the Schottky contact, and the hole mobility with the Lombardi CVT mobility model decreased in this spot.

Figure S2 in the Supplementary Material shows the two-dimensional electric field of the device obtained using the Lombard CVT mobility model. The values of V_a and lattice temperature were 2 V and 300 K respectively. The electric field led to a decrease in both μ_ac and μ_sr in the Lombardi CVT mobility model. We also simulated the forward I–V characteristics using the Lombardi CVT mobility model at 200, 300, 400, and 500 K, as shown in Figure S3 of the Supplementary Material. The extracted V_f and R_on,sp at various temperatures of the device using Lombardi CVT mobility model are shown in Table 2. The values of V_f at 200, 300, 400, and 500 K were 2.84, 5.17, 9.11, and 15.49 V, respectively. The values of R_on,sp at 200, 300, 400, and 500 K were 17.2, 40.8, 82.0, and 145.8 mΩ∙cm², respectively. The decrease in lattice temperature suppressed the scattering of μ_ac and μ_b. The Lombardi CVT mobility model is suitable for numerical simulation of diamond devices under high electric field, because it considers the mobility reduction due to the electric field.

3.4. Empirical Mobility Model

We also investigated the hole mobility based on the experimental results from Volpe et al. [22,29]. They reported that ionized impurity scattering was the dominant scattering mechanism, and that the room temperature mobility was limited by crystalline defects. They proposed the mobility equation given below, which is based on experimental results:

$${\mu }_p\left(\mathrm{T},{\mathrm{N}}_a\right)=\mathsf{\mu }\left(300\mathrm{K},N_a\right){\left(\frac{T}{300}\right)}^{-\beta \left(N_a\right)}$$

(4)

where ${\mu }_p\left(300\mathrm{K},N_a\right)$, $\beta \left(N_a\right)$, μ_max, μ_min, N_μ, γ_μ, β_max, β_min, N_β, and γ_β were ${\mu }_{min}+\frac{{\mu }_{max}-{\mu }_{min}}{1+{\left(\frac{N_a}{N_{\mu }}\right)}^{{\gamma }_{\mu }}}$, ${\beta }_{min}+\frac{{\beta }_{max}-{\beta }_{min}}{1+{\left(\frac{N_a}{N_{\beta }}\right)}^{{\gamma }_{\beta }}}$, 2016 cm²/Vs, 0 cm²/Vs, 3.25 × 10¹⁷ cm⁻³, 0.73, 3.11, 0, 4.1 × 10¹⁸ cm⁻³, and 0.617, respectively, for our devices. The hole mobility at 300 K and β(N_a) obtained from the empirical model were 1990 cm²/Vs and 3.092, respectively, for our device structure. We inputted the parameters and simulated the devices. Figure 8 shows the forward I–V characteristics of the p-type pseudo-vertical diamond SBD obtained using the empirical mobility model at 300, 400, and 500 K, respectively. The values of V_f at 100 A/cm² were 1.77, 2.65, and 4.20 V at 300, 400, and 500 K, respectively. These values can be converted into R_on,sp values of 6.8, 16.8, and 33.7 mΩ∙cm² at 300, 400, and 500 K, respectively. The hole mobilities calculated from the equation at 300, 400, and 500 K were 1990, 820, and 410 cm²/Vs, respectively, identical to the values extracted from the numerical simulation.

The built-in potential, hole mobility, V_f and R_on,sp using constant, analytic, Lombardi CVT, and empirical mobility models are compared in Table 2. The hole mobility using Lombardi CVT mobility model was not added in Table 2 because the electric field influenced the hole mobility. It is noted that the hole mobility model determined the V_f and R_on,sp. The scattering-related forward current using Lombardi CVT model was also adjusted by a scattering factor. We defined the scattering factor of 1 in this work. When the device operates at the high field, the Lombardi CVT mobility model is appropriate because it considers the field-dependent mobility degradation. However, the safe operating area should be limited by the maximum junction temperature, so the diamond power devices should be used at the low on-current density. The empirical mobility model is suitable, compared with the constant and analytic mobility models because it is based on experimental results. The simulated R_on,sp compared with the experimental result from the literature. The simulated R_on,sp of 6.8 mΩ∙cm² using the empirical mobility model was less than the experimental one of 18.5 mΩ∙cm² [15]. This difference was caused by the epitaxy quality and fabrication process. The diamond technology has not been optimized unlike conventional silicon, and various material and fabrication methods exist. The trap level, trap density, Fermi-level pinning, and Ohmic contact resistance were not considered in this work because the epitaxy growth and fabrication process of the diamond semiconductors are still developing. This result based on the hole mobility can help the numerical studies for the diamond devices.

3.5. Breakdown Voltage

We investigated the device geometry using the empirical mobility model. If one parameter was changed, the other parameters were fixed for comparison. We also simulated the breakdown voltage of the devices using Selberherr’s impact ionization model [34]. The impact ionization coefficients, α_n and α_p, for electrons and holes, respectively, were calculated using the following equations [35,36]:

$${\alpha }_n=A_{n}exp\left[-{\left(\frac{B_n}{E}\right)}^{C_n}\right]$$

(5)

$${\alpha }_p=A_{p}exp\left[-{\left(\frac{B_p}{E}\right)}^{C_p}\right]$$

(6)

where A_n, A_p, B_n, B_p, C_n, and C_p are fitting parameters and E is the electric field in the direction of the current. We modified the fitting parameters so that the breakdown field of the parallel-plane Schottky contact/p- drift layer of 10 MV/cm was satisfied [25].

Figure 9 shows the simulated V_f and breakdown voltage of the p-type pseudo-vertical diamond SBDs with values of t_drift of 3.0, 4.0, 4.6, 5.0, and 6.0 μm. We used the empirical mobility model for the forward I–V. The forward I–V characteristics are also included in the Supplementary Material as Figure S4. The values of V_f with t_drift of 3.0, 4.0, 4.6, 5.0, and 6.0 μm were 1.60, 1.71, 1.77, 1.80, and 1.87 at 100 A/cm², respectively. Converting these values to R_on,sp gives 5.1, 6.2, 6.8, 7.1, and 7.8 mΩ∙cm², respectively. The breakdown voltage of the devices with values of t_drift of 3.0, 4.0, 4.6, 5.0, and 6.0 μm were 990, 1120, 1190, 1230, and 1310 V, respectively. An increase in t_drift increased the resistance of the p- drift layer, which in turn decreased the forward current. However, this expanded the depletion region at the p- drift layer, which increased the breakdown voltage.

Figure 10 shows the simulated V_f and breakdown voltage of the devices with values of l_cathode of 0.5, 1.0, 2.0, and 3.0 μm, respectively. The empirical mobility model used for the forward I–V characteristics. The forward I–V characteristics are also included in the Supplementary Material as Figure S5. The values of V_f of the devices with l_cathode of 0.5, 1.0, 2.0, and 3.0 were 2.29, 2.03, 1.77, and 1.61 V at 100 A/cm², respectively. Converting these values to R_on,sp gives 12.0, 9.4, 6.8, and 5.2 mΩ∙cm², respectively. The narrow Schottky contact increased the current crowding and on-resistance during conduction. When the l_cathode decreased from 1.0 to 0.5 μm, the breakdown voltage decreased slightly from 1140 to 1040 V. This was caused by a decrease in the depletion area under the Schottky contact. When the l_cathode was longer than 1.0 μm, the breakdown voltage did not change considerably.

Finally, we simulated the forward and reverse characteristics of the p-type pseudo-vertical diamond SBDs with empirical mobility and modified impact ionization models [25,29]. The empirical mobility model [29] was suitable for the numerical simulation at the low field because it is based on experimental results. The device achieved a low value of R_on,sp of 6.8 mΩ∙cm², a high breakdown voltage of 1190 V, and a high figure-of-merit of 210 MW/cm². The figure-of-merit was the square of the breakdown voltage divided by the value of R_on,sp. The diamond devices promise low power loss and high energy conversion efficiency in the power systems.

4. Conclusions

The forward I–V characteristics of p-type pseudo-vertical diamond SBDs were investigated; the use of various mobility models was important because this resulted in different values of V_f and R_on,sp. The analytic mobility model uses a mobility that changes with doping concentration, while the constant mobility model fixes the mobility absolutely. The Lombardi CVT mobility model considers the perpendicular electric field, doping concentration, and temperature-dependent scattering. This led to mobility degradation at the edge of the Schottky contact where the electric field was concentrated. The empirical mobility model had the advantage of being based on experimental results. The p-type diamond pseudo-vertical SBD achieved high performance, with a value of R_on,sp of 6.8 mΩ∙cm², a breakdown voltage of 1190 V, and a figure-of-merit of 210 MW/cm². Diamond power devices with a high breakdown field and high thermal conductivity are suitable for power switching devices that could replace Si and SiC devices.