An Electrokinetically-Driven Microchip for Rapid Entrapment and Detection of Nanovesicles
Abstract
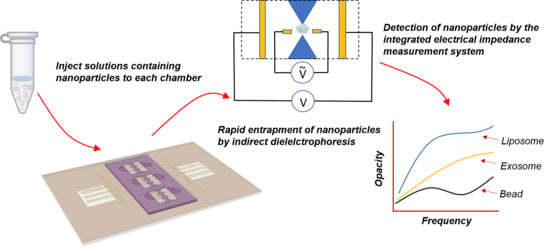
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Preparation of Sub-Micron Particles
2.3. Device Layout and Fabrication
2.4. Particle Trapping and Impedance Measurement
2.5. Finite Element Analysis
2.6. Theoretical Modeling and Equivalent Circuit
3. Results and Discussion
3.1. Particles Entrapment
3.2. Impedance Measurement of Solution with Various Ionic Strengths
3.3. Impedance Measurements of Sub-Micron Particles in Solution
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sohn, L.; Saleh, O.; Facer, G.; Beavis, A.; Allan, R.; Notterman, D.A. Capacitance cytometry: Measuring biological cells one by one. Proc. Natl. Acad. Sci. USA 2000, 97, 10687–10690. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- MacCuspie, R.I.; Nuraje, N.; Lee, S.-Y.; Runge, A.; Matsui, H. Comparison of electrical properties of viruses studied by AC capacitance scanning probe microscopy. J. Am. Chem. Soc. 2008, 130, 887–891. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Holmes, D.; Pettigrew, D.; Reccius, C.H.; Gwyer, J.D.; van Berkel, C.; Holloway, J.; Davies, D.E.; Morgan, H. Leukocyte analysis and differentiation using high speed microfluidic single cell impedance cytometry. Lab A Chip 2009, 9, 2881–2889. [Google Scholar] [CrossRef] [PubMed]
- Chen, N.-C.; Chen, C.-H.; Chen, M.-K.; Jang, L.-S.; Wang, M.-H. Single-cell trapping and impedance measurement utilizing dielectrophoresis in a parallel-plate microfluidic device. Sens. Actuators B Chem. 2014, 190, 570–577. [Google Scholar] [CrossRef]
- Haandbæk, N.; Bürgel, S.C.; Heer, F.; Hierlemann, A. Characterization of subcellular morphology of single yeast cells using high frequency microfluidic impedance cytometer. Lab A Chip 2014, 14, 369–377. [Google Scholar] [CrossRef]
- Höber, R. Eine Methode, die elektrische Leitfähigkeit im Innern von Zellen zu messen. Pflüger’s Arch. Für Die Gesamte Physiol. Des Menschen Und Der Tiere 1910, 133, 237–253. [Google Scholar]
- Fricke, H. The electric capacity of suspensions with special reference to blood. J. Gen. Physiol. 1925, 9, 137–152. [Google Scholar] [CrossRef]
- Curtis, H.J.; Cole, K.S. Transverse electric impedance of Nitella. J. Gen. Physiol. 1937, 21, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Heileman, K.; Daoud, J.; Tabrizian, M. Dielectric spectroscopy as a viable biosensing tool for cell and tissue characterization and analysis. Biosens. Bioelectron. 2013, 49, 348–359. [Google Scholar] [CrossRef]
- Moore, J.H.; Salahi, A.; Honrado, C.; Warburton, C.; Warren, C.A.; Swami, N.S. Quantifying bacterial spore germination by single-cell impedance cytometry for assessment of host microbiota susceptibility to Clostridioides difficile infection. Biosens. Bioelectron. 2020, 166, 112440. [Google Scholar] [CrossRef]
- Clausen, C.H.; Dimaki, M.; Bertelsen, C.V.; Skands, G.E.; Rodriguez-Trujillo, R.; Thomsen, J.D.; Svendsen, W.E. Bacteria detection and differentiation using impedance flow cytometry. Sensors 2018, 18, 3496. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGrath, J.; Honrado, C.; Spencer, D.; Horton, B.; Bridle, H.; Morgan, H. Analysis of parasitic protozoa at the single-cell level using microfluidic impedance cytometry. Sci. Rep. 2017, 7, 2601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGrath, J.; Honrado, C.; Moore, J.; Adair, S.; Varhue, W.; Salahi, A.; Farmehini, V.; Goudreau, B.; Nagdas, S.; Blais, E. Electrophysiology-based Stratification of Pancreatic Tumorigenicity by Label-free Single-Cell Impedance Cytometry. Anal. Chim. Acta 2019, 1101, 90–98. [Google Scholar] [CrossRef] [PubMed]
- Cho, Y.H.; Yamamoto, T.; Sakai, Y.; Fujii, T.; Kim, B. Development of microfluidic device for electrical/physical characterization of single cell. J. Microelectromech. Syst. 2006, 15, 287–295. [Google Scholar] [CrossRef]
- Gawad, S.; Schild, L.; Renaud, P. Micromachined impedance spectroscopy flow cytometer for cell analysis and particle sizing. Lab A Chip 2001, 1, 76–82. [Google Scholar] [CrossRef]
- Holmes, D.; Morgan, H. Single cell impedance cytometry for identification and counting of CD4 T-cells in human blood using impedance labels. Anal. Chem. 2010, 82, 1455–1461. [Google Scholar] [CrossRef]
- Sun, T.; Bernabini, C.; Morgan, H. Single-colloidal particle impedance spectroscopy: Complete equivalent circuit analysis of polyelectrolyte microcapsules. Langmuir 2009, 26, 3821–3828. [Google Scholar] [CrossRef]
- Ayliffe, H.E.; Frazier, A.B.; Rabbitt, R. Electric impedance spectroscopy using microchannels with integrated metal electrodes. J. Microelectromech. Syst. 1999, 8, 50–57. [Google Scholar] [CrossRef]
- Iliescu, C.; Poenar, D.P.; Carp, M.; Loe, F.C. A microfluidic device for impedance spectroscopy analysis of biological samples. Sens. Actuators B Chem. 2007, 123, 168–176. [Google Scholar] [CrossRef]
- Zong, X.; Zhu, R.; Guo, X. Nanostructured gold microelectrodes for SERS and EIS measurements by incorporating ZnO nanorod growth with electroplating. Sci. Rep. 2015, 5, 16454. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.H.; Varhue, W.B.; Su, Y.-H.; Linton, S.S.; Farmehini, V.; Fox, T.E.; Matters, G.L.; Kester, M.; Swami, N.S. Conductance-based biophysical distinction and microfluidic enrichment of nanovesicles derived from pancreatic tumor cells of varying invasiveness. Anal. Chem. 2019, 91, 10424–10431. [Google Scholar] [CrossRef] [PubMed]
- Ayala-Mar, S.; Perez-Gonzalez, V.H.; Mata-Gómez, M.A.; Gallo-Villanueva, R.C.; González-Valdez, J. Electrokinetically driven exosome separation and concentration using dielectrophoretic-enhanced pdms-based microfluidics. Anal. Chem. 2019, 91, 14975–14982. [Google Scholar] [CrossRef] [PubMed]
- Alazzam, A.; Stiharu, I.; Bhat, R.; Meguerditchian, A.N. Interdigitated comb-like electrodes for continuous separation of malignant cells from blood using dielectrophoresis. Electrophoresis 2011, 32, 1327–1336. [Google Scholar] [CrossRef]
- Wang, L.; Lu, J.; Marchenko, S.A.; Monuki, E.S.; Flanagan, L.A.; Lee, A.P. Dual frequency dielectrophoresis with interdigitated sidewall electrodes for microfluidic flow-through separation of beads and cells. Electrophoresis 2009, 30, 782–791. [Google Scholar] [CrossRef] [PubMed]
- Yasukawa, T.; Suzuki, M.; Shiku, H.; Matsue, T. Control of the microparticle position in the channel based on dielectrophoresis. Sens. Actuators B Chem. 2009, 142, 400–403. [Google Scholar] [CrossRef]
- Shi, L.; Rana, A.; Esfandiari, L. A low voltage nanopipette dielectrophoretic device for rapid entrapment of nanoparticles and exosomes extracted from plasma of healthy donors. Sci. Rep. 2018, 8, 6751. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Kuhnell, D.; Borra, V.J.; Langevin, S.M.; Nakamura, T.; Esfandiari, L. Rapid and label-free isolation of small extracellular vesicles from biofluids utilizing a novel insulator based dielectrophoretic device. Lab A Chip 2019, 19, 3726–3734. [Google Scholar] [CrossRef]
- Gawad, S.; Cheung, K.; Seger, U.; Bertsch, A.; Renaud, P. Dielectric spectroscopy in a micromachined flow cytometer: Theoretical and practical considerations. Lab A Chip 2004, 4, 241–251. [Google Scholar] [CrossRef]
- Chen, J.; Xue, C.; Zhao, Y.; Chen, D.; Wu, M.-H.; Wang, J. Microfluidic impedance flow cytometry enabling high-throughput single-cell electrical property characterization. Int. J. Mol. Sci. 2015, 16, 9804–9830. [Google Scholar] [CrossRef] [Green Version]
- Norlin, A.; Pan, J.; Leygraf, C. Investigation of interfacial capacitance of Pt, Ti and TiN coated electrodes by electrochemical impedance spectroscopy. Biomol. Eng. 2002, 19, 67–71. [Google Scholar] [CrossRef]
- Sun, T.; Green, N.G.; Gawad, S.; Morgan, H. Analytical electric field and sensitivity analysis for two microfluidic impedance cytometer designs. IET Nanobiotechnol. 2007, 1, 69–79. [Google Scholar] [CrossRef] [Green Version]
- Minteer, S.D. Microfluidic Techniques: Reviews and Protocols; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 321. [Google Scholar]
- Laohakunakorn, N.; Thacker, V.V.; Muthukumar, M.; Keyser, U.F. Electroosmotic flow reversal outside glass nanopores. Nano Lett. 2015, 15, 695–702. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S.; Liu, M.; Tai, Y.-C. Micro coulter counters with platinum black electroplated electrodes for human blood cell sensing. Biomed. Microdevices 2008, 10, 221–231. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.; Zhu, R.; Zong, X. A microchip integrating cell array positioning with in situ single-cell impedance measurement. Analyst 2015, 140, 6571–6578. [Google Scholar] [CrossRef] [PubMed]
- Robinson, D.A. The electrical properties of metal microelectrodes. Proc. IEEE 1968, 56, 1065–1071. [Google Scholar] [CrossRef]
- Lima, L.F.; Vieira, A.L.; Mukai, H.; Andrade, C.M.; Fernandes, P.R. Electric impedance of aqueous KCl and NaCl solutions: Salt concentration dependence on components of the equivalent electric circuit. J. Mol. Liq. 2017, 241, 530–539. [Google Scholar] [CrossRef]
- Yoon, G. Dielectric properties of glucose in bulk aqueous solutions: Influence of electrode polarization and modeling. Biosens. Bioelectron. 2011, 26, 2347–2353. [Google Scholar] [CrossRef]
- Schwan, H. Electrode polarization impedance and measurements in biological materials. Ann. New York Acad. Sci. 1968, 148, 191–209. [Google Scholar] [CrossRef]
- Maxwell, J.C. Preface to the First Edition, a Treatise on Electricity and Magnetism; Dover Publications: New York, NY, USA, 1954; Volume 1. [Google Scholar]
- Zheng, L.; Brody, J.P.; Burke, P.J. Electronic manipulation of DNA, proteins, and nanoparticles for potential circuit assembly. Biosens. Bioelectron. 2004, 20, 606–619. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R.; Sullivan, B.D.; Mifflin, R.L.; Esener, S.C.; Heller, M.J. Alternating current electrokinetic separation and detection of DNA nanoparticles in high-conductance solutions. Electrophoresis 2008, 29, 1765–1774. [Google Scholar] [CrossRef]
- Weng, P.-Y.; Chen, I.-A.; Yeh, C.-K.; Chen, P.-Y.; Juang, J.-Y. Size-dependent dielectrophoretic crossover frequency of spherical particles. Biomicrofluidics 2016, 10, 011909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cui, L.; Holmes, D.; Morgan, H. The dielectrophoretic levitation and separation of latex beads in microchips. Electrophoresis 2001, 22, 3893–3901. [Google Scholar] [CrossRef]
- Hong, J.; Yoon, D.S.; Kim, S.K.; Kim, T.S.; Kim, S.; Pak, E.Y.; No, K. AC frequency characteristics of coplanar impedance sensors as design parameters. Lab A Chip 2005, 5, 270–279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jen, C.-P.; Chen, T.-W. Selective trapping of live and dead mammalian cells using insulator-based dielectrophoresis within open-top microstructures. Biomed. Microdevices 2009, 11, 597. [Google Scholar] [CrossRef]
- Chiou, C.-H.; Pan, J.-C.; Chien, L.-J.; Lin, Y.-Y.; Lin, L., Jr. Characterization of microparticle separation utilizing electrokinesis within an electrodeless dielectrophoresis chip. Sensors 2013, 13, 2763–2776. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Q.; Yuan, Y. Application of vertical electrodes in microfluidic channels for impedance analysis. Micromachines 2016, 7, 96. [Google Scholar] [CrossRef] [Green Version]
- Tsai, S.L.; Wang, M.H.; Chen, M.K.; Jang, L.S. Analytical and numerical modeling methods for electrochemical impedance analysis of single cells on coplanar electrodes. Electroanalysis 2014, 26, 389–398. [Google Scholar] [CrossRef]
- Iliescu, C.; Poenar, D.P.; Selvan, S.T. Frequency dependence on the accuracy of electrical impedance spectroscopy measurements in microfluidic devices. J. Micromech. Microeng. 2009, 20, 022001. [Google Scholar] [CrossRef]
- Jang, L.-S.; Wang, M.-H. Microfluidic device for cell capture and impedance measurement. Biomed. Microdevices 2007, 9, 737–743. [Google Scholar] [CrossRef]
- Gómez, R.; Bashir, R.; Bhunia, A.K. Microscale electronic detection of bacterial metabolism. Sens. Actuators B Chem. 2002, 86, 198–208. [Google Scholar] [CrossRef]
- Haandbæk, N.; Bürgel, S.C.; Heer, F.; Hierlemann, A. Resonance-enhanced microfluidic impedance cytometer for detection of single bacteria. Lab A Chip 2014, 14, 3313–3324. [Google Scholar] [CrossRef] [PubMed]
- Chan, K.L.; Gascoyne, P.R.; Becker, F.F.; Pethig, R. Electrorotation of liposomes: Verification of dielectric multi-shell model for cells. Biochim. Et Biophys. Acta (Bba)-Lipids Lipid Metab. 1997, 1349, 182–196. [Google Scholar] [CrossRef]
- Tamkovich, S.; Tutanov, O.; Laktionov, P. Exosomes: Generation, structure, transport, biological activity, and diagnostic application. Biochem. (Mosc.) Suppl. Ser. A Membr. Cell Biol. 2016, 10, 163–173. [Google Scholar] [CrossRef]
- Clarke, R.W.; Piper, J.D.; Ying, L.; Klenerman, D. Surface conductivity of biological macromolecules measured by nanopipette dielectrophoresis. Phys. Rev. Lett. 2007, 98, 198102. [Google Scholar] [CrossRef] [PubMed]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Esfandiari, L. An Electrokinetically-Driven Microchip for Rapid Entrapment and Detection of Nanovesicles. Micromachines 2021, 12, 11. https://doi.org/10.3390/mi12010011
Shi L, Esfandiari L. An Electrokinetically-Driven Microchip for Rapid Entrapment and Detection of Nanovesicles. Micromachines. 2021; 12(1):11. https://doi.org/10.3390/mi12010011
Chicago/Turabian StyleShi, Leilei, and Leyla Esfandiari. 2021. "An Electrokinetically-Driven Microchip for Rapid Entrapment and Detection of Nanovesicles" Micromachines 12, no. 1: 11. https://doi.org/10.3390/mi12010011
APA StyleShi, L., & Esfandiari, L. (2021). An Electrokinetically-Driven Microchip for Rapid Entrapment and Detection of Nanovesicles. Micromachines, 12(1), 11. https://doi.org/10.3390/mi12010011