Multi Parameter Flow Meter for On-Line Measurement of Gas Mixture Composition †
Abstract
:1. Introduction
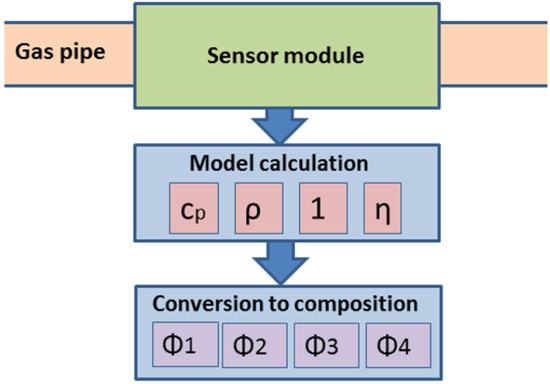
2. System and Model


3. Results and Discussion

3.1. MEMS Sensor


3.2. Steel Sensor Technology


| Property/Component | Nitrogen | Carbon-dioxide | Hydrogen | Methane | Argon |
|---|---|---|---|---|---|
| Density (kg/m3) | 1.150 | 1.815 | 0.083 | 0.659 | 1.64 |
| Heat capacity (J/kg·K) | 1040 | 846.9 | 14300 | 2204 | 521.9 |
| Viscosity (Pa·s) | 1.75 × 10−5 | 1.45 ×·10−5 | 8.8 ×·10−6 | 1.10 ×·10−5 | 2.26 ×·10−5 |
| Heat conductivity (W/(m·K)) | 0.0260 | 0.0165 | 0.1760 | 0.0327 | 0.01763 |
| Density × heat capacity (J/m3·K) | 1196 | 1537 | 1187 | 1452 | 856 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mouris, A.J. Optimized Fired Heater Control; Hydrocarbon Processing: Houston, TX, USA, 2010; pp. 65–68. [Google Scholar]
- Ulbig, P.; Hoburg, D. Determination of the calorific value of natural gas by different methods. Thermochim. Acta 2002, 382, 27–35. [Google Scholar] [CrossRef]
- Udina, S.; Carmona, M.; Pardo, A.; Calaza, C.; Santander, J.; Fonseca, L.; Marco, S. A micromachined thermoelectric sensor for natural gas analysis: Multivariate calibration results. Sens. Actuators B Chem. 2012, 551–558. [Google Scholar]
- Sparks, D.; Smith, R.; Riley, D.; Tran, N.; Patel, J.; Chimbayo, A.; Najafi, N. Monitoring and Blending Biofuels Using a Microfluidic Sensor. J. ASTM Int. 2010, 7, 1–9. [Google Scholar] [CrossRef]
- Harsányi, G. Polymer films in sensor applications: A review of present uses and future possibilities. Sens. Rev. 2000, 20, 98–105. [Google Scholar] [CrossRef]
- Arshak, K.; Moore, E.; Lyons, G.M.; Harris, J.; Clifford, S. A review of gas sensors employed in electronic nose applications. Sens. Rev. 2004, 24, 181–198. [Google Scholar] [CrossRef]
- Liu, X.; Cheng, S.; Liu, H.; Hu, S.; Zhang, D.; Ning, H. A survey on gas sensing technology. Sensors 2012, 127, 9635–9665. [Google Scholar] [CrossRef]
- Baker, R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Lötters, J.C.; van der Wouden, E.; Groenesteijn, J.; Sparreboom, W.; Lammerink, T.S.J.; Wiegerink, R.J. Integrated multi-parameter flow measurement system. In Proceedings of the 27th International Conference on Micro Electro Mechanical Systems (MEMS 2014), San Francisco, CA, USA, 26–30 January 2014; pp. 975–978.
- Lammerink, T.S.J.; Lötters, J.C.; Wiegerink, R.J.; Groenesteijn, J.; Haneveld, J. Single chip flow sensing system with a dynamic flow range of more than 4 decades. In Proceedings of the 16th International Solid-State Sensors, Actuators and Microsystems Conference (Transducers 2011), Beijing, China, 5–9 June 2011; pp. 890–893.
- Haneveld, J.; Lammerink, T.S.J.; De Boer, M.J.; Sanders, R.G.P.; Mehendale, A.; Lötters, J.C.; Dijkstra, M.; Wiegerink, R.J. Modeling, design, fabrication and characterization of a micro Coriolis mass flow sensor. J. Micromechanics Microeng. 2010, 20, 125001. [Google Scholar] [CrossRef]
- Sparreboom, W.; van de Geest, J.; Katerberg, M.; Postma, F.; Haneveld, J.; Groenesteijn, J.; Lammerink, T.; Wiegerink, R.; Lötters, J. Compact mass flow meter based on a micro Coriolis flow sensor. Micromachines 2013, 4, 22–33. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van der Wouden, E.; Groenesteijn, J.; Wiegerink, R.; Lötters, J. Multi Parameter Flow Meter for On-Line Measurement of Gas Mixture Composition. Micromachines 2015, 6, 452-461. https://doi.org/10.3390/mi6040452
Van der Wouden E, Groenesteijn J, Wiegerink R, Lötters J. Multi Parameter Flow Meter for On-Line Measurement of Gas Mixture Composition. Micromachines. 2015; 6(4):452-461. https://doi.org/10.3390/mi6040452
Chicago/Turabian StyleVan der Wouden, Egbert, Jarno Groenesteijn, Remco Wiegerink, and Joost Lötters. 2015. "Multi Parameter Flow Meter for On-Line Measurement of Gas Mixture Composition" Micromachines 6, no. 4: 452-461. https://doi.org/10.3390/mi6040452
APA StyleVan der Wouden, E., Groenesteijn, J., Wiegerink, R., & Lötters, J. (2015). Multi Parameter Flow Meter for On-Line Measurement of Gas Mixture Composition. Micromachines, 6(4), 452-461. https://doi.org/10.3390/mi6040452