A Mathematical Model of Average Dynamics in a Stem Cell Hierarchy Suggests the Combinatorial Targeting of Cancer Stem Cells and Progenitor Cells as a Potential Strategy against Tumor Growth
Abstract
:Simple Summary
Abstract
1. Introduction
2. Methods
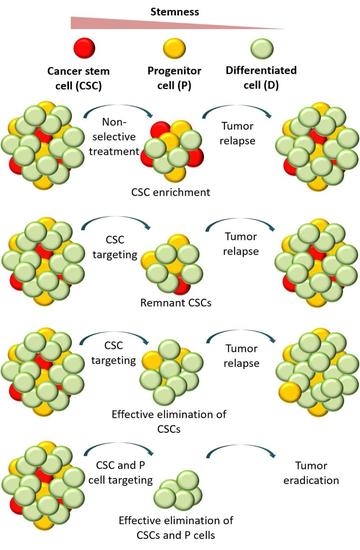
2.1. Hypothesis
- Residual CSCs;
- More differentiated cells regaining a CSC ability;
- Different CSC populations within the same tumor;
- Intermediate progenitor (P) cells that possess enough potency to generate tumors.
2.2. Mathematical Model

3. Results and Discussion
3.1. Tumor Relapse after the Selective Targeting of CSCs
3.2. Comparing Strategies to Combat Cancer
3.2.1. Nonselective Treatment of Tumor Cells
3.2.2. Selective Targeting of Less Differentiated Tumor Cells
3.2.3. Combinatorial Targeting of Less Differentiated Tumor Cells
- (A)
- Selective killing of CSCs and P cells by a 100- and 15-fold augmentation of k6 and k7, and their corresponding death rates in cellular reactions R6 and R7, respectively (Figure 6A);
- (B)
- Enhancement of P cell differentiation into D cells by increasing k5 by 20% in cellular reaction R5, and selectively eliminating CSCs by augmenting k6 100-fold in R6 (Figure 6B);
- (C)
- Inhibition of CSC symmetrical renewal by a 1000-fold reduction in k1 (R1) and selectively killing P cells by a 100-fold increase in k7 (R7) (Figure 6C).
3.3. Further Methods and Models to Verify the Hypothesis
3.3.1. Selective Targeting of CSCs in Combination with Standard-of-Care Chemotherapy in Ovarian Cancer
3.3.2. Sketching an In Vivo Experiment
3.4. Model Limitations
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hanahan, D.; Weinberg, R.A. Hallmarks of Cancer: The Next Generation. Cell 2011, 144, 646–674. [Google Scholar] [CrossRef] [Green Version]
- Lawson, D.A.; Witte, O.N. Stem cells in prostate cancer initiation and progression. J. Clin. Investig. 2007, 117, 2044–2050. [Google Scholar] [CrossRef] [Green Version]
- Codd, A.S.; Kanaseki, T.; Torigo, T.; Tabi, Z. Cancer stem cells as targets for immunotherapy. Immunology 2018, 153, 304–314. [Google Scholar] [CrossRef]
- Reya, T.; Morrison, S.J.; Clarke, M.F.; Weissman, I.L. Stem cells, cancer, and cancer stem cells. Nature 2001, 414, 105–111. [Google Scholar] [CrossRef] [Green Version]
- Tharmapalan, P.; Mahendralingam, M.; Berman, H.K.; Khokha, R. Mammary stem cells and progenitors: Targeting the roots of breast cancer for prevention. EMBO J. 2019, 38, e100852. [Google Scholar] [CrossRef]
- Cho, R.W.; Clarke, M.F. Recent advances in cancer stem cells. Curr. Opin. Genet. Dev. 2008, 18, 48–53. [Google Scholar] [CrossRef]
- Desai, A.; Yan, Y.; Gerson, S.L. Concise Reviews: Cancer Stem Cell Targeted Therapies: Toward Clinical Success. Stem Cells Transl. Med. 2019, 8, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Collins, A.T.; Berry, P.A.; Hyde, C.; Stower, M.J.; Maitland, N.J. Prospective Identification of Tumorigenic Prostate Cancer Stem Cells. Cancer Res. 2005, 65, 10946–10951. [Google Scholar] [CrossRef] [Green Version]
- Patrawala, L.; Calhoun-Davis, T.; Schneider-Broussard, R.; Tang, D.G. Hierarchical organization of prostate cancer cells in xenograft tumors: The CD44+alpha2beta1+ cell population is enriched in tumor-initiating cells. Cancer Res. 2007, 67, 6796–6805. [Google Scholar] [CrossRef] [Green Version]
- Patrawala, L.; Calhoun, T.; Schneider-Broussard, R.; Zhou, J.; Claypool, K.; Tang, D.G. Side population is enriched in tumorigenic, stem-like cancer cells, whereas ABCG2+ and ABCG2- cancer cells are similarly tumorigenic. Cancer Res. 2005, 65, 6207–6219. [Google Scholar] [CrossRef] [Green Version]
- Safa, A.R. Resistance to Cell Death and Its Modulation in Cancer Stem Cells. Crit. Rev. Oncog. 2016, 21, 203–219. [Google Scholar] [CrossRef]
- Yu, J.S. Cancer Stem Cell Antigen Vaccines and Methods. U.S. Patent 8,129,184, 6 March 2012. [Google Scholar]
- Gupta, P.B.; Onder, T.T.; Jiang, G.; Tao, K.; Kuperwasser, C.; Weinberg, R.A.; Lander, E.S. Identification of Selective Inhibitors of Cancer Stem Cells by High-Throughput Screening. Cell 2009, 138, 645–659. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zielske, S.P.; Spalding, A.C.; Wicha, M.S.; Lawrence, T.S. Ablation of Breast Cancer Stem Cells with Radiation. Transl. Oncol. 2011, 4, 227–233. [Google Scholar] [CrossRef] [Green Version]
- Mani, S.A.; Guo, W.; Liao, M.-J.; Eaton, E.N.; Ayyanan, A.; Zhou, A.Y.; Brooks, M.; Reinhard, F.; Zhang, C.C.; Shipitsin, M.; et al. The epithelial-mesenchymal transition generates cells with properties of stem cells. Cell 2008, 133, 704–715. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yeo, S.K.; Guan, J.-L. Breast Cancer: Multiple Subtypes within a Tumor? Trends Cancer 2017, 3, 753–760. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Villadsen, R.; Sørlie, T.; Fogh, L.; Grønlund, S.Z.; Fridriksdottir, A.J.; Kuhn, I.; Rank, F.; Wielenga, V.T.; Solvang, H.; et al. Tumor initiating but differentiated luminal-like breast cancer cells are highly invasive in the absence of basal-like activity. Proc. Natl. Acad. Sci. USA 2012, 109, 6124–6129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsuji, T.; Ibaragi, S.; Shima, K.; Hu, M.G.; Katsurano, M.; Sasaki, A.; Hu, G. Epithelial-mesenchymal transition induced by growth suppressor p12CDK2-AP1 promotes tumor cell local invasion but suppresses distant colony growth. Cancer Res. 2008, 68, 10377–10386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, J.H.; Donaher, J.L.; Murphy, D.A.; Chau, S.; Yang, J. Spatiotemporal regulation of epithelial-mesenchymal transition is essential for squamous cell carcinoma metastasis. Cancer Cell 2012, 22, 725–736. [Google Scholar] [CrossRef] [Green Version]
- Fischer, K.R.; Durrans, A.; Lee, S.; Sheng, J.; Li, F.; Wong, S.T.C.; Choi, H.; El Rayes, T.; Ryu, S.; Troeger, J.; et al. Epithelial-to-mesenchymal transition is not required for lung metastasis but contributes to chemoresistance. Nature 2015, 527, 472–476. [Google Scholar] [CrossRef]
- Zheng, X.; Carstens, J.L.; Kim, J.; Scheible, M.; Kaye, J.; Sugimoto, H.; Wu, C.-C.; LeBleu, V.S.; Kalluri, R. Epithelial-to-mesenchymal transition is dispensable for metastasis but induces chemoresistance in pancreatic cancer. Nature 2015, 527, 525–530. [Google Scholar] [CrossRef] [Green Version]
- Lan, X.; Jörg, D.J.; Cavalli, F.M.G.; Richards, L.M.; Nguyen, L.V.; Vanner, R.J.; Guilhamon, P.; Lee, L.; Kushida, M.M.; Pellacani, D.; et al. Fate mapping of human glioblastoma reveals an invariant stem cell hierarchy. Nature 2017, 549, 227–232. [Google Scholar] [CrossRef]
- Koh, S.P.; Brasch, H.D.; de Jongh, J.; Itinteang, T.; Tan, S.T. Cancer stem cell subpopulations in moderately differentiated head and neck cutaneous squamous cell carcinoma. Heliyon 2019, 5, e02257. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Heidt, D.G.; Dalerba, P.; Burant, C.F.; Zhang, L.; Adsay, V.; Wicha, M.; Clarke, M.F.; Simeone, D.M. Identification of pancreatic cancer stem cells. Cancer Res. 2007, 67, 1030–1037. [Google Scholar] [CrossRef] [Green Version]
- Pádua, D.; Barros, R.; Luísa Amaral, A.; Mesquita, P.; Freire, A.F.; Sousa, M.; Maia, A.F.; Caiado, I.; Fernandes, H.; Pombinho, A.; et al. A SOX2 Reporter System Identifies Gastric Cancer Stem-Like Cells Sensitive to Monensin. Cancers 2020, 12, 495. [Google Scholar] [CrossRef] [Green Version]
- Kemper, K.; Prasetyanti, P.R.; De Lau, W.; Rodermond, H.; Clevers, H.; Medema, J.P. Monoclonal antibodies against Lgr5 identify human colorectal cancer stem cells. Stem Cells 2012, 30, 2378–2386. [Google Scholar] [CrossRef]
- Cortina, C.; Turon, G.; Stork, D.; Hernando-Momblona, X.; Sevillano, M.; Aguilera, M.; Tosi, S.; Merlos-Suárez, A.; Stephan-Otto Attolini, C.; Sancho, E.; et al. A genome editing approach to study cancer stem cells in human tumors. EMBO Mol. Med. 2017, 9, 869–879. [Google Scholar] [CrossRef]
- e Melo, F.d.S.; Kurtova, A.V.; Harnoss, J.M.; Kljavin, N.; Hoeck, J.D.; Hung, J.; Anderson, J.E.; Storm, E.E.; Modrusan, Z.; Koeppen, H.; et al. A distinct role for Lgr5+ stem cells in primary and metastatic colon cancer. Nature 2017, 543, 676–680. [Google Scholar] [CrossRef]
- Fumagalli, A.; Oost, K.C.; Kester, L.; Morgner, J.; Bornes, L.; Bruens, L.; Spaargaren, L.; Azkanaz, M.; Schelfhorst, T.; Beerling, E.; et al. Plasticity of Lgr5-Negative Cancer Cells Drives Metastasis in Colorectal Cancer. Cell Stem Cell 2020, 26, 569–578. [Google Scholar] [CrossRef]
- McDonald, O.G.; Maitra, A.; Hruban, R.H. Human correlates of provocative questions in pancreatic pathology. Adv. Anat. Pathol. 2012, 19, 351–362. [Google Scholar] [CrossRef]
- Bradshaw, A.; Wickremesekera, A.; Brasch, H.D.; Chibnall, A.M.; Davis, P.F.; Tan, S.T.; Itinteang, T. Cancer Stem Cells in Glioblastoma Multiforme. Front. Surg. 2016, 3, 48. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, F.N.; Reisinger, J.; Gomez, K.E.; Chimed, T.-S.; Thomas, C.M.; Le, P.N.; Miller, B.; Morton, J.J.; Nieto, C.M.; Somerset, H.L.; et al. Leading edge or tumor core: Intratumor cancer stem cell niches in oral cavity squamous cell carcinoma and their association with stem cell function. Oral Oncol. 2019, 98, 118–124. [Google Scholar] [CrossRef] [PubMed]
- Munro, M.J.; Wickremesekera, S.K.; Peng, L.; Marsh, R.W.; Itinteang, T.; Tan, S.T. Cancer stem cell subpopulations in primary colon adenocarcinoma. PLoS ONE 2019, 14, e0221963. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoganandarajah, V.; Patel, J.; van Schaijik, B.; Bockett, N.; Brasch, H.D.; Paterson, E.; Sim, D.; Davis, P.F.; Roth, I.M.; Itinteang, T.; et al. Identification of Cancer Stem Cell Subpopulations in Head and Neck Metastatic Malignant Melanoma. Cells 2020, 9, 324. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.H.; Featherston, T.; Tan, S.T.; Chibnall, A.M.; Brasch, H.D.; Davis, P.F.; Itinteang, T. Characterization of Cancer Stem Cells in Moderately Differentiated Buccal Mucosal Squamous Cell Carcinoma. Front. Surg. 2016, 3, 46. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Cong, Y.; Wang, D.; Sun, Y.; Deng, L.; Liu, Y.; Martin-Trevino, R.; Shang, L.; McDermott, S.P.; Landis, M.D.; et al. Breast Cancer Stem Cells Transition between Epithelial and Mesenchymal States Reflective of their Normal Counterparts. Stem Cell Rep. 2014, 2, 78–91. [Google Scholar] [CrossRef]
- Kern, S.E.; Shibata, D. The Fuzzy Math of Solid Tumor Stem Cells: A Perspective. Cancer Res. 2007, 67, 8985–8988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molina-Peña, R.; Álvarez, M.M. A Simple Mathematical Model Based on the Cancer Stem Cell Hypothesis Suggests Kinetic Commonalities in Solid Tumor Growth. PLoS ONE 2012, 7, e26233. [Google Scholar] [CrossRef] [Green Version]
- Cocciadiferro, L.; Miceli, V.; Kang, K.-S.; Polito, L.M.; Trosko, J.E.; Carruba, G. Profiling Cancer Stem Cells in Androgen-Responsive and Refractory Human Prostate Tumor Cell Lines. Ann. N. Y. Acad. Sci. 2009, 1155, 257–262. [Google Scholar] [CrossRef]
- Morrison, S.J.; Kimble, J. Asymmetric and symmetric stem-cell divisions in development and cancer. Nature 2006, 441, 1068–1074. [Google Scholar] [CrossRef]
- Dingli, D.; Traulsen, A.; Michor, F. (A)Symmetric Stem Cell Replication and Cancer. PLoS Comput. Biol. 2007, 3, e53. [Google Scholar] [CrossRef] [Green Version]
- Maitland, N.J.; Collins, A.T. Prostate cancer stem cells: A new target for therapy. J. Clin. Oncol. 2008, 26, 2862–2870. [Google Scholar] [CrossRef] [PubMed]
- Tufto, I.; Rofstad, E.K. Interstitial Fluid Pressure, Fraction of Necrotic Tumor Tissue, and Tumor Cell Density in Human Melanoma Xenografts. Acta Oncol. 1998, 37, 291–297. [Google Scholar] [CrossRef]
- Xu, J.; Jiang, X.; Li, H.; Arlinghaus, L.R.; McKinley, E.T.; Devan, S.P.; Hardy, B.M.; Xie, J.; Kang, H.; Chakravarthy, A.B.; et al. Magnetic resonance imaging of mean cell size in human breast tumors. Magn. Reson. Med. 2020, 83, 2002–2014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lyng, H.; Haraldseth, O.; Rofstad, E.K. Measurement of cell density and necrotic fraction in human melanoma xenografts by diffusion weighted magnetic resonance imaging. Magn. Reson. Med. 2000, 43, 828–836. [Google Scholar] [CrossRef]
- Monte, U.D. Does the cell number 109 still really fit one gram of tumor tissue? Cell Cycle 2009, 8, 505–506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bellio, C.; DiGloria, C.; Spriggs, D.R.; Foster, R.; Growdon, W.B.; Rueda, B.R. The Metabolic Inhibitor CPI-613 Negates Treatment Enrichment of Ovarian Cancer Stem Cells. Cancers 2019, 11, 1678. [Google Scholar] [CrossRef] [Green Version]
- Ricci-Vitiani, L.; Lombardi, D.G.; Pilozzi, E.; Biffoni, M.; Todaro, M.; Peschle, C.; De Maria, R. Identification and expansion of human colon-cancer-initiating cells. Nature 2007, 445, 111–115. [Google Scholar] [CrossRef]
- Ovarian Cancer Statistics. How Common is Ovarian Cancer. Available online: https://www.cancer.org/cancer/ovarian-cancer/about/key-statistics.html (accessed on 22 March 2020).
- Martinez-Outschoorn, U.E.; Bartrons, M.; Bartrons, R. Editorial: Cancer Ecosystems. Front. Oncol. 2019, 9, 718. [Google Scholar] [CrossRef]
- Prager, B.C.; Xie, Q.; Bao, S.; Rich, J.N. Cancer Stem Cells: The Architects of the Tumor Ecosystem. Cell Stem Cell 2019, 24, 41–53. [Google Scholar] [CrossRef] [Green Version]
- Junttila, M.R.; Mao, W.; Wang, X.; Wang, B.-E.; Pham, T.; Flygare, J.; Yu, S.-F.; Yee, S.; Goldenberg, D.; Fields, C.; et al. Targeting LGR5 + cells with an antibody-drug conjugate for the treatment of colon cancer. Sci. Transl. Med. 2015, 7, 314ra186–314ra186. [Google Scholar] [CrossRef]
- Kerk, S.A.; Finkel, K.A.; Pearson, A.T.; Warner, K.A.; Zhang, Z.; Nör, F.; Wagner, V.P.; Vargas, P.A.; Wicha, M.S.; Hurt, E.M.; et al. 5T4-Targeted Therapy Ablates Cancer Stem Cells and Prevents Recurrence of Head and Neck Squamous Cell Carcinoma. Clin. Cancer Res. 2017, 23, 2516–2527. [Google Scholar] [CrossRef] [Green Version]








| Reaction | |||
|---|---|---|---|
| R1 | |||
| R2 | |||
| R3 | |||
| R6 | |||
| Total |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Molina-Peña, R.; Tudon-Martinez, J.C.; Aquines-Gutiérrez, O. A Mathematical Model of Average Dynamics in a Stem Cell Hierarchy Suggests the Combinatorial Targeting of Cancer Stem Cells and Progenitor Cells as a Potential Strategy against Tumor Growth. Cancers 2020, 12, 2590. https://doi.org/10.3390/cancers12092590
Molina-Peña R, Tudon-Martinez JC, Aquines-Gutiérrez O. A Mathematical Model of Average Dynamics in a Stem Cell Hierarchy Suggests the Combinatorial Targeting of Cancer Stem Cells and Progenitor Cells as a Potential Strategy against Tumor Growth. Cancers. 2020; 12(9):2590. https://doi.org/10.3390/cancers12092590
Chicago/Turabian StyleMolina-Peña, Rodolfo, Juan Carlos Tudon-Martinez, and Osvaldo Aquines-Gutiérrez. 2020. "A Mathematical Model of Average Dynamics in a Stem Cell Hierarchy Suggests the Combinatorial Targeting of Cancer Stem Cells and Progenitor Cells as a Potential Strategy against Tumor Growth" Cancers 12, no. 9: 2590. https://doi.org/10.3390/cancers12092590
APA StyleMolina-Peña, R., Tudon-Martinez, J. C., & Aquines-Gutiérrez, O. (2020). A Mathematical Model of Average Dynamics in a Stem Cell Hierarchy Suggests the Combinatorial Targeting of Cancer Stem Cells and Progenitor Cells as a Potential Strategy against Tumor Growth. Cancers, 12(9), 2590. https://doi.org/10.3390/cancers12092590