Habitat Imaging of Tumors Enables High Confidence Sub-Regional Assessment of Response to Therapy
Abstract
:Simple Summary
Abstract
1. Introduction
2. Materials and Methods
2.1. Preparation of Tumor Cohorts
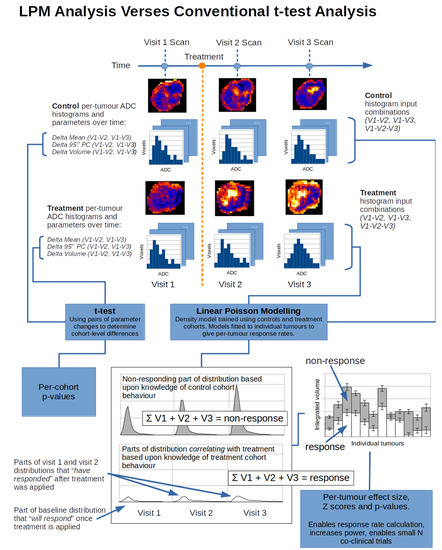
2.2. MRI Acquisition and Analysis
2.3. LPM Modelling and Effect Detection
2.4. Monte Carlo Simulation
2.5. Power Calculations
3. Results
3.1. LPM Determines Multi-Time Point Model Complexity
3.2. Confining Parameter Analysis to Treated Tissue Improves t-Tests
3.3. LPM Detects Biological Response Rates across a Range of Therapies
3.4. LPM Detects Biological Response Rates across a Range of Tumor Models
3.5. LPM Achieves Consistently High True Positive Rates
3.6. Validation of Power Calculations
3.7. LPM Makes Small N Co-Clinical Trials Feasible
4. Discussion
4.1. LPM Is an Alternative Paradigm for Pre-Clinical Cancer Research
4.2. Origins of Additional Power of LPM
4.3. New Experimental Designs
4.4. 3Rs and Cost Benefits
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADC | Apparent Diffusion Co-efficient |
| AI | Artificial intellegence |
| ATV | Atovaquone |
| ANOVA | Analysis of variance |
| AQ4N | Banoxantrone |
| CT | computed tomography |
| FCRT | Fractionate Chemo-radiotherapy |
| FPR | False Positive Rate |
| FNR | False Negative Rate |
| LPM | Linear Poisson Model |
| LOO | Leave one out |
| MRI | Magnetic resonance imaging |
| PET | Positron emission tomography |
| RT | Radiotherapy |
| SD | Standard deviation |
Appendix A
Appendix A.1. Tumor Propagation for Each Cell Line
Appendix A.2. Expectation Maximisation Algorithm
References
- O’Connor, J.P.B.; Rose, C.J.; Waterton, J.C.; Carano, R.A.D.; Parker, G.J.M.; Jackson, A. Imaging Intratumor Heterogeneity: Role in Therapy Response, Resistance, and Clincical Outcome. Clin. Cancer Res. 2015, 21, 249–257. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jardim-Perassi, B.V.; Huang, S.; Dominguez-Viqueira, W.; Poleszczuk, J.; Budzevich, M.M.; Abdalah, M.A.; Pillai, E.R.; Bui, M.M.; Zuccari, D.A.P.C.; Gillies, R.J.; et al. Multiparametric MRI and Coregistered Histology Identify Tumor Habitats in Breast Cancer Mouse Models. Cancer Res. 2019, 79, 3952–3964. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- de Jong, M.; Essers, J.; van Weerden, W.M. Imaging preclinical tumor models: Improving translational power. Nat. Rev. Cancer 2014, 14, 481–493. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.R.W.; Carragher, N.O.; Timpson, P. Developments in preclinical cancer imaging: Innovating the discovery of therapeutics. Nat. Rev. Cancer 2014, 14, 314–328. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, J.P.; Aboagye, E.O.; Adams, J.E.; Aerts, H.J.; Barrington, S.F.; Beer, A.J.; Boellaard, B.; Bohndiek, S.E.; Brady, M.; Brown, G.; et al. Imaging biomarker roadmap for cancer studies. Nat. Rev. Clin. Oncol. 2017, 14, 169–186. [Google Scholar] [CrossRef] [PubMed]
- Clarke, L.P.; Velthuizen, R.P.; Camacho, M.A.; Heine, J.J.; Vaidyanathan, M.; Hall, L.O.; Thatcher, R.W.; Silbiger, M.L. MRI segmentation: Methods and applications. Magn. Reson. Imaging 1995, 13, 343–368. [Google Scholar] [CrossRef]
- Kazerouni, A.S.; Hormuth, D.A., II; Davis, T.; Bloom, M.J.; Mounho, S.; Rahman, G.; Virostko, J.; Yankeelov, T.E.; Sorace, A.G. Quantifying Tumor Heterogeneity via MRI Habitats to Characterize Microenvironmental Alterations in HER2+ Breast Cancer. Cancers 2022, 14, 1837. [Google Scholar] [CrossRef] [PubMed]
- Hamstra, D.A.; Galbán, C.J.; Meyer, C.R.; Johnson, T.D.; Sundgren, P.C.; Tsien, C.; Lawrence, T.S.; Junck, L.; Ross, D.J.; Rehemtulla, A. Functional Diffusion Map As an Early Imaging Biomarker for High-Grade Glioma: Correlation With Conventional Radiologic Response and Overall Survival. J. Clin. Oncol. 2008, 26, 3387–3394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berry, L.R.; Barck, K.H.; Go, M.A.; Ross, J.; Wu, X.; Williams, S.P.; Gogineni, A.; Cole, M.J.; Van Bruggen, N.; Fuh, G.; et al. Quantification of viable tumor microvascular characteristics by multispectral analysis. Magn. Reson. Med. 2008, 60, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Salem, A.; Little, R.A.; Latif, A.; Featherstone, A.K.; Babur, M.; Peset, I.; Cheung, S.; Watson, Y.; Tessyman, V.; Mistry, H.; et al. Oxygen-enhanced MRI Is Feasible, Repeatable, and Detects Radiotherapy-induced Change in Hypoxia in Xenograft Models and in Patients with Non–small Cell Lung Cancer. Clin. Cancer Res. 2019, 25, 3818–3829. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tar, P.D.; Thacker, N.A.; Gilmour, J.D.; Jones, M.A. Automated quantitative measurements and associated error covariances for planetary image analysis. Adv. Space Res. 2015, 56, 92–105. [Google Scholar] [CrossRef]
- Deepaisarn, S.; Tar, P.D.; Thacker, N.A.; Seepujak, A.; McMahon, A.W. Quantifying biological samples using Linear Poisson Independent Component Analysis for MALDI-ToF mass spectra. Bioinformatics 2018, 34, 1001–1008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tar, P.D.; Thacker, N.A.; Babur, M.; Watson, Y.; Cheung, S.; Little, R.A.; Gieling, R.G.; Williams, K.J.; O’Connor, J.P.B. A new method for the high-precision assessment of tumor changes in response to treatment. Bioinformatics 2018, 34, 2625–2633. [Google Scholar] [CrossRef] [Green Version]
- Workman, P.; Aboagye, E.O.; Balkwill, F.; Balmain, A.; Bruder, G.; Chaplin, J.D.; Double, J.A.; Everitt, J.; Farningham, D.A.H.; Glennie, M.J.; et al. Guidelines for the welfare and use of animals in cancer research. Br. J. Cancer 2010, 102, 1555–1577. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clohessy, J.G.; Pandolfi, P.P. Mouse hospital and co-clinical trial project–from bench to bedside. Nat. Rev. Clin. Oncol. 2015, 12, 491–508. [Google Scholar] [CrossRef] [PubMed]
- Padhani, A.R.; Liu, G.; Koh, D.M. Diffusion-weighted magnetic resonance imaging as a cancer biomarker: Consensus and recommendations. Neoplasia 2009, 11, 491–508. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McHugh, D.J.; Lipowska-Bhalla, G.; Babur, M.; Watson, Y.; Peset, I.; Mistry, H.B.; Hubbard-Cristinacce, P.L.; Naish, J.H.; Honeychurch, J.; Williams, K.J.; et al. Diffusion model comparison identifies distinct tumor sub-regions and tracks treatment response. Magn. Reson. Med. 2020, 84, 1250–1263. [Google Scholar] [CrossRef] [PubMed]
- Workman, P.; Aboagye, E.O.; Chung, Y.L.; Griffiths, J.R.; Hart, R.; Leach, M.O.; Maxwell, R.J.; McSheehy, P.M.J.; Price, P.M. Minimally Invasive Pharmacokinetic and Pharmacodynamic Technologies in Hypothesis-Testing Clinical Trials of Innovative Therapies. J. Natl. Cancer Inst. 2006, 98, 580–598. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Whisenant, J.G.; Sorace, A.G.; McIntyre, J.O.; Kang, H.; Sánchez, V.; Loveless, M.E.; Yankeelov, T.E. Evaluating treatment response using DW-MRI and DCE-MRI in trastuzumab responsive and resistant HER2-overexpressing human breast cancer xenografts. Transl. Oncol. 2014, 7, 768–779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Connor, J.P.; Carano, R.A.; Clamp, A.R.; Ross, J.; Ho, C.C.; Jackson, A.; Parker, G.J.M.; Rose, C.J.; Peale, F.V.; Friesenhahn, M. Quantifying antivascular effects of monoclonal antibodies to vascular endothelial growth factor: Insights from imaging. Clin. Cancer Res. 2009, 15, 6674–6682. [Google Scholar] [CrossRef] [Green Version]










| Xenograft Model | In Plane Maxtrix | Slice Number | In Plane Size | Slice Thickness | Volume |
|---|---|---|---|---|---|
| Calu6 | 64 × 64 | 15 | 0.5 mm × 0.5 mm | 1.0 mm | 0.25 mm |
| U87 | 64 × 64 | 15 | 0.5 mm × 0.5 mm | 1.0 mm | 0.25 mm |
| HCT116 | 64 × 64 | 7 | 0.4 mm × 0.4 mm | 1.2 mm | 0.192 mm |
| CT26 | 64 × 64 | 10 | 0.5 mm × 0.5 mm | 1.2 mm | 0.3 mm |
| 4T1 | 64 × 64 | 10 | 0.5 mm × 0.5 mm | 1.2 mm | 0.3 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tar, P.D.; Thacker, N.A.; Babur, M.; Lipowska-Bhalla, G.; Cheung, S.; Little, R.A.; Williams, K.J.; O’Connor, J.P.B. Habitat Imaging of Tumors Enables High Confidence Sub-Regional Assessment of Response to Therapy. Cancers 2022, 14, 2159. https://doi.org/10.3390/cancers14092159
Tar PD, Thacker NA, Babur M, Lipowska-Bhalla G, Cheung S, Little RA, Williams KJ, O’Connor JPB. Habitat Imaging of Tumors Enables High Confidence Sub-Regional Assessment of Response to Therapy. Cancers. 2022; 14(9):2159. https://doi.org/10.3390/cancers14092159
Chicago/Turabian StyleTar, Paul David, Neil A. Thacker, Muhammad Babur, Grazyna Lipowska-Bhalla, Susan Cheung, Ross A. Little, Kaye J. Williams, and James P. B. O’Connor. 2022. "Habitat Imaging of Tumors Enables High Confidence Sub-Regional Assessment of Response to Therapy" Cancers 14, no. 9: 2159. https://doi.org/10.3390/cancers14092159
APA StyleTar, P. D., Thacker, N. A., Babur, M., Lipowska-Bhalla, G., Cheung, S., Little, R. A., Williams, K. J., & O’Connor, J. P. B. (2022). Habitat Imaging of Tumors Enables High Confidence Sub-Regional Assessment of Response to Therapy. Cancers, 14(9), 2159. https://doi.org/10.3390/cancers14092159