Fractional-Order Edge Detection Masks for Diabetic Retinopathy Diagnosis as a Case Study
Abstract
:1. Introduction
2. Survey on Fractional-Order Image Edge Detection
3. Proposed Fractional-Order Sobel Mask
3.1. Left-Sided Fractional-Order Mask (LS-FOM)
3.2. Right-Sided Fractional-Order Mask (RS-FOM)
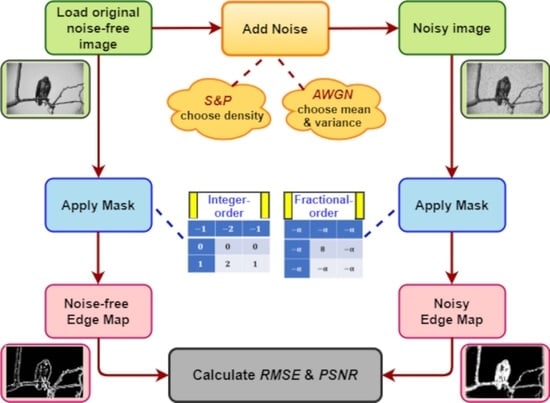
4. Simulation Results
4.1. Noise-Free Images
4.2. Noisy Images
4.2.1. Salt and Pepper Noise
4.2.2. Additive White Gaussian Noise
5. Application: Diabetic Retinopathy Diagnosis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FC | Fractional Calculus | S&P | Salt and Pepper |
| GL | Grunwald–Letnikov | AWGN | Additive White Gaussian noise |
| FO | Fractional Order | RMSE | Root Mean Square Error |
| LS-FOM | left-sided fractional-order mask | PSNR | Peak Signal to Noise Ratio |
| RS-FOM | right-sided fractional-order mask | DR | Diabetic Retinopathy |
| FM | Fractional Mask | BDR | Background Diabetic Retinopathy |
| MRI | Magnetic Resonance Imaging | PDR | Proliferative Diabetic Retinopathy |
| AD | Alzheimer disease | STARE | STructured Analysis of the Retina |
References
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2006. [Google Scholar]
- Torre, V.; Poggio, T.A. On edge detection. IEEE Trans. Pattern Anal. Mach. Intell. 1986, 147–163. [Google Scholar] [CrossRef]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order; Dover Books on Mathematics; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Machado, J.A.T.; Kiryakova, V. Recent history of the fractional calculus: Data and statistics. In Basic Theory; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany, 2019; pp. 1–22. [Google Scholar]
- Elwy, O.; Abdelaty, A.; Said, L.; Radwan, A. Fractional calculus definitions, approximations, and engineering applications. J. Eng. Appl. Sci. 2020, 67, 1–30. [Google Scholar]
- Allagui, A.; Freeborn, T.J.; Elwakil, A.S.; Fouda, M.E.; Maundy, B.J.; Radwan, A.G.; Said, Z.; Abdelkareem, M.A. Review of fractional-order electrical characterization of supercapacitors. J. Power Sources 2018, 400, 457–467. [Google Scholar] [CrossRef]
- Helmy, A.H.; Ismail, S.M. Fractional-Order Image Edge Detector on FPGA. In Proceedings of the 2018 30th International Conference on Microelectronics (ICM), Sousse, Tunisia, 16–19 December 2018; pp. 339–342. [Google Scholar] [CrossRef]
- Said, L.A.; Radwan, A.G.; Madian, A.H.; Soliman, A.M. Three fractional-order-capacitors-based oscillators with controllable phase and frequency. J. Circuits Syst. Comput. 2017, 26, 1750160. [Google Scholar] [CrossRef] [Green Version]
- Tolba, M.F.; Elsafty, A.H.; Armanyos, M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Synchronization and FPGA realization of fractional-order Izhikevich neuron model. Microelectron. J. 2019, 89, 56–69. [Google Scholar] [CrossRef]
- Ismail, S.M.; Said, L.A.; Radwan, A.G.; Madian, A.H.; Abu-ElYazeed, M.F. A novel image encryption system merging fractional-order edge detection and generalized chaotic maps. Signal Process. 2020, 167, 107280. [Google Scholar] [CrossRef]
- Soliman, N.S.; Tolba, M.F.; Said, L.A.; Madian, A.H.; Radwan, A.G. Fractional X-shape Controllable Multi-scroll Attractor with Parameter Effect and FPGA Automatic Design Tool software. Chaos Solitan Fractals 2019, 126, 292–307. [Google Scholar] [CrossRef]
- Sayed, W.S.; Ismail, S.M.; Said, L.A.; Radwan, A.G. On the fractional order generalized discrete maps. In Mathematical Techniques of Fractional Order Systems; Elsevier: Amsterdam, The Netherlands, 2018; pp. 375–408. [Google Scholar]
- Ismail, S.M.; Radwan, A.G.; Madian, A.H.; Abu-ElYazeed, M.F. Comparative study of fractional filters for alzheimer disease detection on MRI images. In Proceedings of the International Conference on Telecommunications and Signal Processing (TSP), Vienna, Austria, 27–29 June 2016; pp. 720–723. [Google Scholar]
- Abdel-Gawad, A.H.; Said, L.A.; Radwan, A.G. Optimized Edge Detection Technique for Brain Tumor Detection in MR Images. IEEE Access 2020, 8, 136243–136259. [Google Scholar] [CrossRef]
- Pu, Y. Fractional calculus approach to texture of digital image. In Proceedings of the IEEE International Conference on Signal Processing (ICSP), Guilin, China, 16–20 November 2006; pp. 1002–1006. [Google Scholar]
- Chen, J.; Huang, C.; Du, Y.; Lin, C. Combining fractional-order edge detection and chaos synchronisation classifier for fingerprint identification. IET Image Process 2014, 8, 354–362. [Google Scholar] [CrossRef]
- Chi, C.; Gao, F. Palm Print Edge Extraction Using Fractional Differential Algorithm. J. Appl. Math. 2014, 2014. [Google Scholar] [CrossRef]
- Pu, Y.-F. Fractional differential analysis for texture of digital image. J. Algorithms Comput. Technol. 2007, 1, 357–380. [Google Scholar] [CrossRef]
- Jia, H.; Pu, Y. Fractional calculus method for enhancing digital image of bank slip. In Proceedings of the Congress on Image and Signal Processing, Sanya, China, 27–30 May 2008; Volume 3, pp. 326–330. [Google Scholar]
- Marazzato, R.; Sparavigna, A.C. Astronomical image processing based on fractional calculus: The AstroFracTool. arXiv 2009, arXiv:0910.4637. [Google Scholar]
- Dong, F.; Chen, Y. A Fractional-order derivative based variational framework for image denoising. Inverse Problems Imaging 2016, 10, 27–50. [Google Scholar] [CrossRef] [Green Version]
- Hemalatha, S.; Anouncia, S.M. Anouncia, S.M. A computational model for texture analysis in images with fractional differential filter for texture detection. In Biometrics: Concepts, Methodologies, Tools, and Applications; IGI Global: Vellore, India, 2017; pp. 309–332. [Google Scholar]
- Ghanbari, B.; Atangana, A. A new application of fractional Atangana-Baleanu derivatives: Designing ABC-fractional masks in image processing. Phys. A Stat. Mech. Its Appl. 2019. [Google Scholar] [CrossRef]
- Telke, C.; Beitelschmidt, M. Edge detection based on fractional order differentiation and its application to railway track images. Pamm 2015, 15, 671–672. [Google Scholar] [CrossRef]
- He, C.; Ye, Y.Q.; Jiang, B.; Zhou, X. A novel edge detection method based on fractional-order calculus mask. Acta Autom. Sin. 2012, 38, 776–787. [Google Scholar] [CrossRef]
- Wang, W.X.; Li, W.S.; Yu, X. Fractional differential algorithms for rock fracture images. Imaging Sci. J. 2012, 60, 103–111. [Google Scholar] [CrossRef]
- Amoako-Yirenkyi, P.; Appati, J.K.; Dontwi, I.K. A new construction of a fractional derivative mask for image edge analysis based on Riemann-Liouville fractional derivative. Adv. Differ. Equ. 2016, 2016, 238. [Google Scholar] [CrossRef] [Green Version]
- Daou, R.A.Z.; El Samarani, F.; Yaacoub, C.; Moreau, X. Fractional Derivatives for Edge Detection: Application to Road Obstacles. In Smart Cities Performability, Cognition, & Security; Springer: Cham, Switzerland, 2020; pp. 115–137. [Google Scholar]
- Tian, D.; Wu, J.F.; Yang, Y.J. A fractional-order Sobel operator for medical image structure feature extraction. In Advanced Materials Research; Trans Tech Publications Ltd.: Bäch, Switzerland, 2014; Volume 860, pp. 2910–2913. [Google Scholar]
- Chen, Q.; Huang, G.; Men, T.; Qin, H.; Wang, M. Fractional differential algorithm for texture and contrast enhancement. In Proceedings of the Eighth International Conference on Digital Image Processing (ICDIP), Chengdu, China, 20–22 May 2016; International Society for Optics and Photonics: Bellingham, WA, USA, 2016; Volume 10033, p. 1003323. [Google Scholar]
- Bist, A.; Sondhi, S.G. Fractional Order Approach for Edge Detection of Low Contrast Images. Master’s Thesis, Thapar Institute of Engineering and Technology, Punjab, India, 2017. [Google Scholar]
- Nandal, A.; Gamboa-Rosales, H.; Dhaka, A.; Celaya-Padilla, J.M.; Galvan-Tejada, J.I.; Galvan-Tejada, C.E.; Martinez-Ruiz, F.J.; Guzman-Valdivia, C. Image edge detection using fractional calculus with feature and contrast enhancement. Circuits Syst. Signal Process. 2018, 37, 3946–3972. [Google Scholar] [CrossRef]
- Tian, D.; Wu, J.; Yang, Y. A Fractional-order Edge Detection Operator for Medical Image Structure Feature Extraction. In Proceedings of the 26th IEEE Chinese Control and Decision Conference, Changsha, China, 31 May–2 June 2014; pp. 5173–5176. [Google Scholar]
- Bento, T.; Valério, D.; Teodoro, P.; Martins, J. Fractional Order Image Processing of Medical Images. J. Appl. Nonlinear Dyn. 2017, 6, 181–191. [Google Scholar] [CrossRef]
- ElAraby, W.S.; Madian, A.H.; Ashour, M.A.; Farag, I.; Nassef, M. Fractional edge detection based on genetic algorithm. In Proceedings of the 2017 29th International Conference on Microelectronics (ICM), Hamra, Beirut, 10–13 December 2017; pp. 1–4. [Google Scholar]
- John, R.; Kunju, N. Detection of Alzhemier’s Disease Using Fractional Edge Detection. Glob. J. Technol. Optim. 2019, 9. [Google Scholar] [CrossRef]
- Lavín-Delgado, J.E.; Solís-Pérez, J.E.; Gómez-Aguilar, J.F.; Escobar-Jiménez, R.F. A New Fractional-Order Mask for Image Edge Detection Based on Caputo–Fabrizio Fractional-Order Derivative without Singular Kernel. Circuits Syst. Signal Process. 2019, 39, 1419–1448. [Google Scholar] [CrossRef]
- Pan, X.; Zhu, J.; Yu, H.; Chen, L.; Liu, Y.; Li, L. Robust corner detection with fractional calculus for magnetic resonance imaging. Biomed. Signal Process. Control 2021, 63, 102112. [Google Scholar] [CrossRef]
- Kaur, K.; Jindal, N.; Singh, K. Fractional Fourier Transform based Riesz fractional derivative approach for edge detection and its application in image enhancement. Signal Process. 2021, 180, 107852. [Google Scholar] [CrossRef]
- Lv, H.; Zhang, F.; Wang, R. Robust Active Contour Model Using Patch-Based Signed Pressure Force and Optimized Fractional-Order Edge. IEEE Access 2021, 9, 8771–8785. [Google Scholar] [CrossRef]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives; Gordon and Breach Science Publishers: Yverdon, Switzerland, 1993; Volume 1993. [Google Scholar]
- The Berkley Segmentation Dataset and Benchmark. 2007. Available online: https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/segbench/ (accessed on 5 March 2021).
- Mansour, R.F. Evolutionary computing enriched computer-aided diagnosis system for diabetic retinopathy: A survey. IEEE Rev. Biomed. Eng. 2017, 10, 334–349. [Google Scholar] [CrossRef] [PubMed]
- Fraz, M.M.; Remagnino, P.; Hoppe, A.; Uyyanonvara, B.; Rudnicka, A.R.; Owen, C.G.; Barman, S.A. Blood vessel segmentation methodologies in retinal images-a survey. Comput. Methods Programs Biomed. 2012, 108, 407–433. [Google Scholar] [CrossRef] [PubMed]
- Ismail, S.M. Fractional-Order Image Segmentation for Security Surveillance. In Proceedings of the 32nd International Conference on Microelectronics (ICM), Aqaba, Jordan, 14–16 December 2020. [Google Scholar]
- Yazid, H.; Arof, H.; Mokhtar, N. Edge sharpening for diabetic retinopathy detection. In Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems (CIS), Singapore, 28–30 June 2010; pp. 41–44. [Google Scholar]
- Sivakamasundari, J.; Kavitha, G.; Natarajan, V.; Ramakrishnan, S. Proposal of a Content Based retinal Image Retrieval system using Kirsch template based edge detection. In Proceedings of the International Conference in Informatics, Electronics & Vision (ICIEV), Dhaka, Bangladesh, 23–24 May 2014; pp. 1–5. [Google Scholar]
- Dutta, M.K.; Srivastava, K.; Ganguly, S.; Parthasarathi, M.; Burget, R.; Prinosil, J. Exudates detection in digital fundus image using edge based method & strategic thresholding. In Proceedings of the 38th International Conference On Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 9–11 July 2015; pp. 748–752. [Google Scholar]
- Tasgaonkar, M.; Khambete, M. Using differential morphological profiles for microaneurysm detection in diabetic retinal fundus images. In Proceedings of the International Conference on Signal and Information Processing (IConSIP), Nanded, India, 6–8 October 2016; pp. 1–5. [Google Scholar]
- Hoover, A. Structured Analysis of the Retina. 2018. Available online: http://www.ces.clemson.edu/-ahoover/stare (accessed on 5 March 2021).

















| Roberts | Sobel | Prewitt | ||||
|---|---|---|---|---|---|---|
| Operator |  |  |  |  |  |  |
| Edge images |  |  |  | |||
| [15] FM 1 |  | ||
| [15] FM 2 |  | ||
| [15] FM 3 |  | ||
| [16] |  | ||
| [17] |  | [29] FO Sobel |  |
| Noisy Tree | |||||||
| Masks | Integer-order | Fractional-order | |||||
| Sobel | Prewitt | Roberts | FM1 [15] (α = 0.5) | FM2 [15] (α = 0.4) | LS-FOM (α = 0.2) | RS-FOM (α = 0.1) | |
| RMSE | 0.4147 | 0.4135 | 0.3649 | 0.3395 | 0.3071 | 0.2219 | 0.2124 |
| PSNR (dB) | 7.6459 | 7.6713 | 8.7575 | 9.3838 | 10.2534 | 13.0778 | 13.4567 |
| Noisy Players | |||||||
| Masks | Integer-order | Fractional-order | |||||
| Sobel | Prewitt | Laplacian | FM [17] (α = 0.3) | FM [29] (α = 0.2) | LS-FOM (α = 0.3) | RS-FOM (α = 0.2) | |
| RMSE | 0.4780 | 0.4744 | 0.4889 | 0.2142 | 0.3559 | 0.2207 | 0.1894 |
| PSNR (dB) | 6.4115 | 6.4777 | 6.2164 | 13.3849 | 8.9744 | 13.1255 | 14.4522 |
| Noisy Starfish | |||||||
| Masks | Integer-order | Fractional-order | |||||
| Sobel | Prewitt | Roberts | FM1 [15] (α = 0.3) | FM2 [15] (α = 0.4) | LS-FOM (α = 0.3) | RS-FOM (α = 0.4) | |
| RMSE | 0.3662 | 0.3497 | 0.4066 | 0.3495 | 0.3102 | 0.2679 | 0.2512 |
| PSNR (dB) | 8.7264 | 9.1265 | 7.8167 | 9.1299 | 10.1672 | 11.4411 | 12.0005 |
| Noisy Tower | |||||||
| Masks | Integer-order | Fractional-order | |||||
| Sobel | Prewitt | Laplacian | FM3 [15] (α = 0.4) | FM [29] (α = 0.2) | LS-FOM (α = 0.1) | RS-FOM (α = 0.4) | |
| RMSE | 0.2525 | 0.2454 | 0.4935 | 0.2163 | 0.1664 | 0.1481 | 0.1879 |
| PSNR (dB) | 11.9539 | 12.2026 | 6.1344 | 13.2993 | 15.5782 | 16.5883 | 14.5193 |
 |
| Normal | BDR | PDR | |||||||
|---|---|---|---|---|---|---|---|---|---|
| NOR1 | NOR2 | NOR3 | BDR1 | BDR2 | BDR3 | PDR1 | PDR2 | PDR3 | |
| Sobel | 0.1063 | 0.1103 | 0.1075 | 0.2014 | 0.1737 | 0.1833 | 0.1808 | 0.3097 | 0.2763 |
| Robert | 0.0939 | 0.1037 | 0.0944 | 0.1782 | 0.1606 | 0.1440 | 0.1546 | 0.2717 | 0.2564 |
| FM1 α = 0.2 | 0.0905 | 0.0953 | 0.0917 | 0.1603 | 0.1554 | 0.1569 | 0.2270 | 0.2796 | 0.2652 |
| FM2 α = 0.3 | 0.0916 | 0.0920 | 0.0877 | 0.1637 | 0.1567 | 0.1644 | 0.2162 | 0.2841 | 0.2758 |
| FM3 α = 0.4 | 0.0839 | 0.0841 | 0.0775 | 0.1581 | 0.1579 | 0.1576 | 0.2096 | 0.2726 | 0.2819 |
| LS-FOM α = 0.4 | 0.0990 | 0.0959 | 0.0919 | 0.1666 | 0.1585 | 0.1670 | 0.2264 | 0.2838 | 0.2668 |
| RS-FOM α = 0.6 | 0.1237 | 0.1234 | 0.1088 | 0.1591 | 0.1617 | 0.1626 | 0.2306 | 0.2659 | 0.2571 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ismail, S.M.; Said, L.A.; Madian, A.H.; Radwan, A.G. Fractional-Order Edge Detection Masks for Diabetic Retinopathy Diagnosis as a Case Study. Computers 2021, 10, 30. https://doi.org/10.3390/computers10030030
Ismail SM, Said LA, Madian AH, Radwan AG. Fractional-Order Edge Detection Masks for Diabetic Retinopathy Diagnosis as a Case Study. Computers. 2021; 10(3):30. https://doi.org/10.3390/computers10030030
Chicago/Turabian StyleIsmail, Samar M., Lobna A. Said, Ahmed H. Madian, and Ahmed G. Radwan. 2021. "Fractional-Order Edge Detection Masks for Diabetic Retinopathy Diagnosis as a Case Study" Computers 10, no. 3: 30. https://doi.org/10.3390/computers10030030
APA StyleIsmail, S. M., Said, L. A., Madian, A. H., & Radwan, A. G. (2021). Fractional-Order Edge Detection Masks for Diabetic Retinopathy Diagnosis as a Case Study. Computers, 10(3), 30. https://doi.org/10.3390/computers10030030