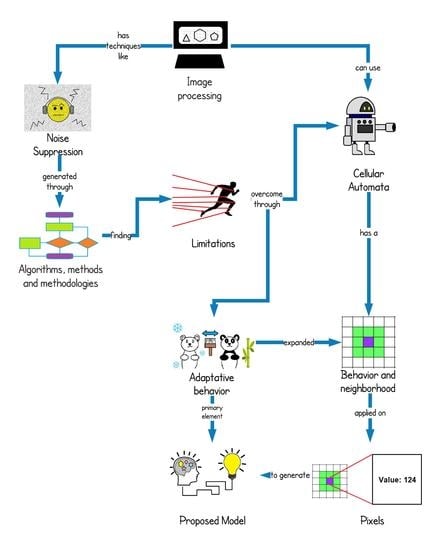
Modeling and Numerical Validation for an Algorithm Based on Cellular Automata to Reduce Noise in Digital Images
Abstract
:1. Introduction
Proposal Approach and Document Organization
2. Background
2.1. Mathematical Modeling
2.2. Noise Elimination
3. Algorithm Based on Cellular Automata
- (a)
- Cells or lattice.
- (b)
- Neighborhood or adjacent neighbors.
- (c)
- Rules for cell transitions.
- : D-dimensional space of integers.
- S: finite set of to the states of A.
- N: finite ordered subset of that corresponds to the neighborhood of A.
- : local rule (transition function) of A.
3.1. Cellular Automata Algorithm to Eliminate Noise in Digital Images
3.2. Cellular Automata Behavioral Model
4. Simulation Validation
- N: Population size.
- Z: 95% confidence level .
- p: Probability of success .
- q: Probability of failure .
- d: Accuracy .
5. Discussion
- Selection of the type of algorithms to be compared considering: reported performance, actuality, available code, number of citations, proposed approach of the algorithm. Some algorithms to consider consist on cellular automata-based algorithmic approaches for noise removal in digital images as Outer Totalistic Cellular Automata (OTCA) [45], and other developments like the presented in [10,46,47,48,49,50,51,52]; likewise, hybrid methods that incorporate cellular automata and fuzzy logic [32,53], as well as modifications and improvements of median filter as Unsymmetric Trimmed Median Filter (UTMF) [54], median-type noise detectors [34], and implementations using local image statistics [33]. Other approaches could also be considered, including algorithms based on dictionary learning methods [11,12], non-negative matrix factorization [13,14], and robust principal component analysis [15,16].
- Type of noise to eliminate considering different algorithms approaches. It can be considered noise additive, multiplicative, impulsive static and dynamic noise [55]. The associated probability distribution can also be considered as: uniform, Gaussian, Poisson, Rayleigh, Speckle, Gamma, White, Brownian, and other noise characteristics like periodic and structural [56].
- Performance metrics considering the operation of the algorithms, in a way that the advantages of each algorithm, can be observed as: processing time, amount of noise removed, image distortion, Mean Absolute Error (MAE), Root Mean Square Error (RMSE), Signal-to-Noise Ratio (SNR), Image Enhancement Factor (IEF), and Structural Similarity Index Measure (SSIM), that is a perceptual metric that quantifies image quality degradation caused by the processing; also the Peak Signal-to-Noise Ratio (PSNR) corresponding to the relationship between the maximum possible energy of a signal and the noise that affects it [44,45,53].
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Marinescu, D. Nature-Inspired Algorithms and Systems; Elsevier: Boston, MA, USA, 2017; pp. 33–63. [Google Scholar] [CrossRef]
- Gong, Y. A survey on the modeling and applications of cellular automata theory. IOP Conf. Ser. Mater. Sci. Eng. 2017, 242, 012106. [Google Scholar] [CrossRef] [Green Version]
- Das, D. A Survey on Cellular Automata and Its Applications; Springer: Berlin/Heidelberg, Germany, 2011; Volume 269. [Google Scholar] [CrossRef]
- Kolnoochenko, A.; Menshutina, N. CUDA-optimized cellular automata for diffusion limited processes. Comput. Aided Chem. Eng. 2015, 37, 551–556. [Google Scholar] [CrossRef]
- Mahata, K.; Sarkar, A.; Das, R.; Das, S. Fuzzy evaluated quantum cellular automata approach for watershed image analysis. In Quantum Inspired Computational Intelligence; Morgan Kaufmann: Boston, MA, USA, 2017; pp. 259–284. [Google Scholar] [CrossRef]
- Baxes, G. Digital Image Processing: Principles and Applications; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- Davies, A. The Focal Digital Imaging A-Z; Focal Press: Oxford, UK, 1998. [Google Scholar]
- Daniel, M. Optica Tradicional y Moderna; Colección “Ciencia para todos”; Fondo de Cultura Económica: Mexico City, Mexico, 2007. [Google Scholar]
- Petrou, M.; Petrou, C. Image Processing: The Fundamentals; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Tourtounis, D.; Mitianoudis, N.; Sirakoulis, G.C. Salt-n-pepper Noise Filtering using Cellular Automata. J. Cell. Autom. 2018, 13, 81–101. [Google Scholar]
- Cai, S.; Kang, Z.; Yang, M.; Xiong, X.; Peng, C.; Xiao, M. Image Denoising via Improved Dictionary Learning with Global Structure and Local Similarity Preservations. Symmetry 2018, 10, 167. [Google Scholar] [CrossRef] [Green Version]
- Peng, C.; Cheng, Q. Discriminative Ridge Machine: A Classifier for High-Dimensional Data or Imbalanced Data. IEEE Trans. Neural Net. Learn. Syst. 2021, 32, 2595–2609. [Google Scholar] [CrossRef] [PubMed]
- Farouk, R.M.; Khalil, H.A. Image Denoising based on Sparse Representation and Non-Negative Matrix Factorization. Life Sci. J. 2012, 9, 337–341. [Google Scholar]
- Peng, C.; Zhang, Z.; Kang, Z.; Chen, C.; Cheng, Q. Nonnegative matrix factorization with local similarity learning. Inf. Sci. 2021, 562, 325–346. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, Q.; Chen, Y.; Cheng, Q.; Peng, C. Hyperspectral Image Denoising With Log-Based Robust PCA. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 1634–1638. [Google Scholar] [CrossRef]
- Peng, C.; Chen, Y.; Kang, Z.; Chen, C.; Cheng, Q. Robust principal component analysis: A factorization-based approach with linear complexity. Inf. Sci. 2020, 513, 581–599. [Google Scholar] [CrossRef]
- Vezhnevets, V.; Konushin, V. “GrowCut”—Interactive Multi-Label ND Image Segmentation By Cellular Automata. Graphicon 2004, 1, 150–156. [Google Scholar]
- Marginean, R.; Andreica, A.; Diosan, L.; Bálint, Z. Feasibility of Automatic Seed Generation Applied to Cardiac MRI Image Analysis. Mathematics 2020, 8, 1511. [Google Scholar] [CrossRef]
- Marginean, R.; Andreica, A.; Diosan, L.; Bálint, Z. Butterfly Effect in Chaotic Image Segmentation. Entropy 2020, 22, 1028. [Google Scholar] [CrossRef] [PubMed]
- Velasquez, W.; Alvarez-Alvarado, M.S. Outdoors Evacuation Routes Algorithm Using Cellular Automata and Graph Theory for Uphills and Downhills. Sustainability 2021, 13, 4731. [Google Scholar] [CrossRef]
- Mărginean, R.; Andreica, A.; Dioşan, L.; Bálint, Z. A Transfer Learning Approach on the Optimization of Edge Detectors for Medical Images Using Particle Swarm Optimization. Entropy 2021, 23, 414. [Google Scholar] [CrossRef]
- Fuente, D.; Garibo i Orts, O.; Conejero, J.A.; Urchueguía, J.F. Rational Design of a Genetic Finite State Machine: Combining Biology, Engineering, and Mathematics for Bio-Computer Research. Mathematics 2020, 8, 1362. [Google Scholar] [CrossRef]
- Treml, L.M.; Bartocci, E.; Gizzi, A. Modeling and Analysis of Cardiac Hybrid Cellular Automata via GPU-Accelerated Monte Carlo Simulation. Mathematics 2021, 9, 164. [Google Scholar] [CrossRef]
- Rößler, C.; Breitenecker, F.; Riegler, M. Simulating the Gluing of Wood Particles by Lattice Gas Cellular Automata and Random Walk. Mathematics 2020, 8, 988. [Google Scholar] [CrossRef]
- Angulo, K.; Gil, D.; Espitia, H. A novel algorithm based on cellular automata to eliminate noise in digital images. J. Eng. Appl. Sci. 2019, 14, 3289–3300. [Google Scholar]
- Gil-Sierra, D.G.; Angulo-Sogamoso, K.V.; Espitia-Cuchango, H.E. Integration of an adaptive cellular automaton and a cellular neural network for the impulsive noise suppression and edge detection in digital images. In Proceedings of the 2019 IEEE Colombian Conference on Applications in Computational Intelligence (ColCACI), Barranquilla, Colombia, 5–7 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Angulo, K.; Gil, D.; Espitia, H. Integration of an Adaptive Cellular Automaton and a Cellular Neural Network for the Impulsive Noise Suppression and Edge Detection in Digital Images. In Applications of Computational Intelligence. ColCACI 2019. Communications in Computer and Information Science; Orjuela-Cañón, A., Figueroa-García, J., Arias-Londoño, J., Eds.; Springer: Cham, Switzerland, 2019; Volume 1096, pp. 168–181. [Google Scholar] [CrossRef]
- Angulo, K.; Gil, D.; Espitia, H. Method for Edges Detection in Digital Images Through the Use of Cellular Automata. In Advances and Applications in Computer Science, Electronics and Industrial Engineering. CSEI 2019. Advances in Intelligent Systems and Computing; Nummenmaa, J., Pérez-González, F., Domenech-Lega, B., Vaunat-J, O., Fernández-Peña, F., Eds.; Springer: Cham, Switzerland, 2020; Volume 1078, pp. 3–21. [Google Scholar] [CrossRef]
- Pyt’ev, Y. Mathematical Methods of Subjective Modeling in Scientific Research: I. The Mathematical and Empirical Basis. Mosc. Univ. Phys. Bull. 2018, 73, 1–16. [Google Scholar] [CrossRef]
- Ouvrier-Buffet, C. Exploring Mathematical Definition Construction Processes. Educ. Stud. Math. 2006, 63, 259–282. [Google Scholar] [CrossRef]
- Menskii, M.B. The difficulties in the mathematical definition of path integrals are overcome in the theory of continuous quantum measurements. Theor. Math. Phys. 1992, 93, 1262–1267. [Google Scholar] [CrossRef]
- Sahin, U.; Uguz, S.; Sahin, F. Salt and pepper noise filtering with fuzzy-cellular automata. Comput. Electr. Eng. 2014, 40, 59–69. [Google Scholar] [CrossRef]
- Garnett, R.; Huegerich, T.; Chui, C.; He, W. A universal noise removal algorithm with an impulse detector. IEEE Trans. Image Process. 2005, 14, 1747–1754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, R.; Ho, C.W.; Nikolova, M. Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization. IEEE Trans. Image Process. 2005, 14, 1479–1485. [Google Scholar] [CrossRef]
- Salcido, A. Cellular Automata: Simplicity Behind Complexity; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar]
- Schiff, J. Cellular Automata: A Discrete View of the World; Wiley Series in Discrete Mathematics & Optimization; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Pan, P.Z.; Feng, X.T.; Zhou, H. Solid Cellular Automaton Method for the Solution of Physical Field. In Proceedings of the 2009 WRI World Congress on Computer Science and Information Engineering, Los Angeles, CA, USA, 31 March–2 April 2009; Volume 1, pp. 765–768. [Google Scholar] [CrossRef]
- Shukla, A.P. Training Cellular Automata for Image Edge Detection. Rom. J. Inf. Sci. Technol. 2016, 19, 338–359. [Google Scholar]
- Rosin, P.; Adamatzky, A.; Sun, X. Cellular Automata in Image Processing and Geometry; Springer: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Wongthanavasu, S.; Sadananda, R. A CA-based edge operator and its performance evaluation. J. Vis. Commun. Image Represent. 2003, 14, 83–96. [Google Scholar] [CrossRef]
- Rodríguez del Águila, M.; González-Ramírez, A. Sample size calculation. Allergol. Immunopathol. 2014, 42, 485–492. [Google Scholar] [CrossRef] [PubMed]
- Caicedo, J. Teoría de Grupos; Universidad Nacional de Colombia, Facultad de Ciencias: Bogotá, Colombia, 2004. [Google Scholar]
- Github. Descriptive Statistics. 2022. Available online: https://sdesabbata.github.io/granolarr_v1/Lectures/bookdown/descriptive-statistics.html (accessed on 19 July 2021).
- Gonzalez, R.; Woods, R. Digital Image Processing; Pearson/Prentice Hall: Hoboken, NJ, USA, 2008. [Google Scholar]
- Jeelani, Z.; Qadir, F. Cellular automata-based approach for salt-and-pepper noise filtration. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 365–374. [Google Scholar] [CrossRef]
- Qadir, F.; Shoosha, I.Q. Cellular automata-based efficient method for the removal of high-density impulsive noise from digital images. Int. J. Inf. Technol. 2018, 10, 529–536. [Google Scholar] [CrossRef]
- Qadir, F.; Peer, M.A.; Khan, K.A. Cellular automata based identification and removal of impulsive noise from corrupted images. J. Glob. Res. Comput. Sci. 2012, 3, 17–20. [Google Scholar]
- Jana, B.; Pal, P.; Bhaumik, J. New Image Noise Reduction Schemes Based on Cellular Automata. Int. J. Soft Comput. Eng. 2012, 2, 98–104. [Google Scholar]
- Wongthanavasu, S. Cellular Automata for Medical Image Processing. In Cellular Automata; Salcido, A., Ed.; IntechOpen: Rijeka, Croatia, 2011. [Google Scholar] [CrossRef] [Green Version]
- Rosin, P.L. Image processing using 3-state cellular automata. Comput. Vis. Image Underst. 2010, 114, 790–802. [Google Scholar] [CrossRef]
- Selvapeter, P.J.; Hordijk, W. Cellular automata for image noise filtering. In Proceedings of the 2009 World Congress on Nature Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 193–197. [Google Scholar] [CrossRef]
- Rosin, P.L. Training Cellular Automata for Image Processing. In Image Analysis. SCIA 2005. Lecture Notes in Computer Science; Kalviainen, H., Parkkinen, J., Kaarna, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 195–204. [Google Scholar] [CrossRef] [Green Version]
- Piroozmandan, M.M.; Farokhi, F.; Kangarloo, K.; Jahanshahi, M. Removing the impulse noise from images based on fuzzy cellular automata by using a two-phase innovative method. Optik 2022, 255, 168713. [Google Scholar] [CrossRef]
- Esakkirajan, S.; Veerakumar, T.; Subramanyam, A.N.; PremChand, C.H. Removal of High Density Salt and Pepper Noise Through Modified Decision Based Unsymmetric Trimmed Median Filter. IEEE Signal Process. Lett. 2011, 18, 287–290. [Google Scholar] [CrossRef]
- Owotogbe, J.S.; Ibiyemi, T.S.; Adu, B.A. A Comprehensive Review On Various Types of Noise in Image Processing. Int. J. Sci. Eng. Res. 2019, 10, 388–393. [Google Scholar]
- Patro, P.; Panda, C. A review on: Noise model in digital image processing. Int. J. Eng. Sci. Res. Technol. 2016, 5, 891–897. [Google Scholar]
- De Canditiis, D. Statistical Inference Techniques. In Encyclopedia of Bioinformatics and Computational Biology; Ranganathan, S., Gribskov, M., Nakai, K., Schönbach, C., Eds.; Academic Press: Oxford, UK, 2019; pp. 698–705. [Google Scholar] [CrossRef]
- Lewis, C. Multiple Comparisons. In International Encyclopedia of Education, 3rd ed.; Peterson, P., Baker, E., McGaw, B., Eds.; Elsevier: Oxford, UK, 2010; pp. 312–318. [Google Scholar] [CrossRef]








| Measure | Median | Mean | DK |
|---|---|---|---|
| nbr-val | 381.000 | 381.000 | 381.000 |
| nbr-null | 35.000 | 6.000 | 15.000 |
| nbr-na | 0.000 | 0.000 | 0.000 |
| min | 0.000 | 0.000 | 0.000 |
| max | 175.000 | 147.000 | 175.000 |
| range | 175.000 | 147.000 | 175.000 |
| sum | 26,233.000 | 18,353.000 | 8951.000 |
| median | 80.000 | 41.000 | 15.000 |
| mean | 68.853 | 48.171 | 23.493 |
| SE-mean | 3.679 | 1.930 | 1.238 |
| CI-mean (0.95) | 7.233 | 3.794 | 2.435 |
| var | 5155.663 | 1418.552 | 584.277 |
| std-dev | 71.803 | 37.664 | 24.172 |
| coef-var | 1.043 | 0.782 | 1.029 |
| skewness | 0.447 | 0.794 | 1.994 |
| kurtosis | −1.426 | −0.237 | 6.947 |
| norm-test-SW | 0.767 | 0.920 | 0.807 |
| norm-test-p | 0.000 | 0.000 | 0.000 |
| Algorithm | Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|---|
| Median | 0.00 | 2.00 | 81.00 | 76.45 | 171.00 | 175.00 |
| Mean | 0.00 | 16.00 | 40.00 | 48.32 | 69.00 | 147.00 |
| DK | 0.00 | 7.00 | 15.00 | 23.67 | 35.00 | 171.00 |
| - | Data Median | Data Mean | Data DK |
|---|---|---|---|
| Data Median | 1.0000000 | 0.7158127 | 0.2821712 |
| Data Mean | 0.7158127 | 1.0000000 | 0.2301503 |
| Data DK | 0.2821712 | 0.2301503 | 1.0000000 |
| Noise | Mean | Median | DK | ||||||
|---|---|---|---|---|---|---|---|---|---|
| % | PSNR | SNR | SSIM | PSNR | SNR | SSIM | PSNR | SNR | SSIM |
| 20 | 17.202 | 9.981 | 0.222 | 23.496 | 16.573 | 0.720 | 42.612 | 32.896 | 0.995 |
| 30 | 17.430 | 8.192 | 0.187 | 23.474 | 14.237 | 0.757 | 38.251 | 29.013 | 0.988 |
| 40 | 15.740 | 6.503 | 0.144 | 18.522 | 9.285 | 0.478 | 36.438 | 27.200 | 0.982 |
| 50 | 14.799 | 9.901 | 0.098 | 14.925 | 10.027 | 0.197 | 36.088 | 31.190 | 0.957 |
| 60 | 11.683 | 6.624 | 0.096 | 12.952 | 7.892 | 0.089 | 34.078 | 29.018 | 0.939 |
| 70 | 13.684 | 6.524 | 0.065 | 9.935 | 2.776 | 0.028 | 37.862 | 30.703 | 0.938 |
| 80 | 10.731 | 4.695 | 0.049 | 7.346 | 1.310 | 0.015 | 32.654 | 26.617 | 0.935 |
| 90 | 12.148 | 7.636 | 0.049 | 6.504 | 1.992 | 0.007 | 30.095 | 25.584 | 0.931 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Angulo, K.V.; Gil, D.G.; Espitia, H.E. Modeling and Numerical Validation for an Algorithm Based on Cellular Automata to Reduce Noise in Digital Images. Computers 2022, 11, 46. https://doi.org/10.3390/computers11030046
Angulo KV, Gil DG, Espitia HE. Modeling and Numerical Validation for an Algorithm Based on Cellular Automata to Reduce Noise in Digital Images. Computers. 2022; 11(3):46. https://doi.org/10.3390/computers11030046
Chicago/Turabian StyleAngulo, Karen Vanessa, Danilo Gustavo Gil, and Helbert Eduardo Espitia. 2022. "Modeling and Numerical Validation for an Algorithm Based on Cellular Automata to Reduce Noise in Digital Images" Computers 11, no. 3: 46. https://doi.org/10.3390/computers11030046
APA StyleAngulo, K. V., Gil, D. G., & Espitia, H. E. (2022). Modeling and Numerical Validation for an Algorithm Based on Cellular Automata to Reduce Noise in Digital Images. Computers, 11(3), 46. https://doi.org/10.3390/computers11030046