Comparison of Statistical and Machine-Learning Models on Road Traffic Accident Severity Classification
Abstract
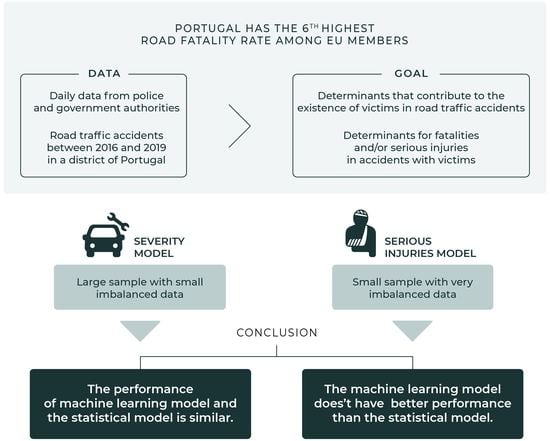
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data
- Fatal: victim who dies.
- Serious injury: victim whose bodily injury requires hospitalization for more than 24 h and who does not die within 30 days of the accident.
- Minor injury: victim whose bodily injury does not require hospitalization, or whose hospitalization is less than 24 h and who does not die within 30 days of the accident.
- Accidents: county, accident location, type of accident, type and name of the road, type of roadside, type of lane, road conservation state, the existence of works on the road, the existence of light signals, the existence of pavement marks, the existence and type of damage on the road, existence of nearby health facilities, total and type of victims, driver escaping from the location of the accident, causes of the accident and date and time of the accident.
- Vehicles: type of vehicle, class and category of vehicle, a vehicle with or without a trailer, if the vehicle burned, tire conditions, the existence of insurance and number of occupants.
- Drivers: gender, date of birth, alcohol and drugs control, existence and year of driving license, driving time, the occurrence of driving manoeuvres and use of safety accessories.
- Victims: type of victim, use of safety accessories, injury severity of the victim within 30 days and if the victim is a pedestrian in circulation.
- Atmospheric conditions: precipitation, temperature, humidity, wind speed, the occurrence of hail and the existence of fog or smoke clouds.
2.3. Statistical and Machine-Learning Models
3. Results
3.1. Severity Model
- Temporal factors: accidents occur in the months of June to October; between Friday and Sunday; between 11 p.m. to 1 a.m. and between 6 a.m. to 7 a.m. (when compared with the ones between 1 a.m. to 4 a.m.), or between 7 a.m. to 11 p.m. (when compared with the ones between 5 a.m. and 6 a.m.), or between 4 a.m. and 5 a.m. (when compared with the ones between 11 p.m. and 1 a.m. and between 6 a.m. and 7 a.m.);
- Weather factors: the wind speed decreases;
- Driver and vehicle factors: accidents do not involve light vehicles (when compared with the ones involving light vehicles); accidents do not involve heavy vehicles (when compared with the ones involving heavy vehicles); accidents involve motorcycles (when compared with the ones not involving motorcycles); the age of the vehicles involved increases; and the maximum age of the drivers involved increases until 46 years and decreases when the maximum age of the drivers involved in the accidents is over 62 years old (when compared with an accident where the maximum age of drivers is 20 years);
- Geographical factors: accidents occur in the municipality of Alcácer do Sal, Grândola, Moita, Palmela, Santiago do Cacém, Seixal and Sesimbra; accidents occur on national roads (EN), due to crashes (when compared with the ones that occur by collision); and accidents involve a pedestrian that occurs on other roads (when compared with the ones that occur on a highway/bridges); and
- Accident-related factors: accidents where there was no escape; and the number of drivers increases.
3.2. Serious Injuries Model
- Geographical factors: the accidents occur in the municipalities of Alcochete, Alcácer do Sal and Palmela;
- Temporal factors: the accidents occur between Thursday and Monday; between 2 a.m. to 5 a.m. and between 6 a.m. to 7 a.m. or between 8 p.m. to 2 a.m., 5 a.m. to 6 a.m. and 7 a.m. to 8 a.m. (when compared to the ones that occur between 8 a.m. to 8 p.m.);
- Road characteristics: the accidents occurred on an IC/IP or on an EN; the accidents occurred on a road where the lanes do not have a central separator; the accidents occur inside urban areas when the roadside is not paved; and the accidents occur on a road with a paved roadside outside an urban area;
- Driver characteristics: the majority of drivers involved are male; and the age of the youngest driver involved in the accident increases;
- Victim characteristics: the age of the oldest victim involved in the accident increases; and
- Vehicle features: the median age of the vehicles involved in the accident increases; in collision accidents, those involving heavy vehicles and those not involving heavy vehicles but involving motorbikes (when compared to the ones involving only light vehicles); and in accidents involving only light vehicles, those that occur by pedestrian running over and those by crashing (when compared to those that occur by collision).
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | Highway |
| ANSR | Autoridade Nacional de Segurança Rodoviária (National Road Safety Authority) |
| BEAV | Statistical Bulletin of Road Traffic Accidents |
| CT-GNR | Territorial Command of the GNR |
| EN | National Road |
| GNR | Guarda Nacional Republicana (National Republican Guard) |
| IC | Complementary Itinerary |
| IP | Principal Itinerary |
| IPMA | Instituto Português do Mar e da Atmosfera (Portuguese Institute for Sea and Atmosphere) |
| KNN | K-Nearest Neighbour |
| MOPREVIS | Modeling and Prediction of Road Traffic Accidents in the District of Setúbal |
| PSP | Polícia de Segurança Pública (Public Security Police) |
| SVM | Support Vector Machine |
References
- Belokurov, V.; Spodarev, R.; Belokurov, S. Determining passenger traffic as important factor in urban public transport system. Transp. Res. Procedia 2020, 50, 52–58. [Google Scholar] [CrossRef]
- World Health Organization. Global Status Report on Road Safety 2018. 2018. Available online: https://apps.who.int/iris/bitstream/handle/10665/276462/9789241565684-eng.pdf?sequence=1&isAllowed=y (accessed on 25 January 2022).
- Eurostat. Road Accidents: Number of Fatalities Continues Falling. 2021. Available online: https://ec.europa.eu/eurostat/en/web/products-eurostat-news/-/ddn-20210624-1 (accessed on 25 January 2022).
- Lusa. Sinistralidade Rodoviária tem Impacto Económico e Social Negativo de 1.2% do PIB-Governo. 2018. Available online: https://www.rtp.pt/noticias/pais/sinistralidade-rodoviaria-tem-impacto-economico-e-social-negativo-de-12-do-pib-governo_n1112193 (accessed on 25 January 2022).
- Savolainen, P.T.; Mannering, F.L.; Lord, D.; Quddus, M.A. The statistical analysis of highway crash-injury severities: A review and assessment of methodological alternatives. Accid. Anal. Prev. 2011, 43, 1666–1676. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Garrido, R.; Bastos, A.; de Almeida, A.; Elvas, J.P. Prediction of road accident severity using the ordered probit model. Transp. Res. Procedia 2014, 3, 214–223. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Li, Z.; Pu, Z.; Xu, C. Comparing prediction performance for crash injury severity among various machine learning and statistical methods. IEEE Access 2018, 6, 60079–60087. [Google Scholar] [CrossRef]
- Silva, P.B.; Andrade, M.; Ferreira, S. Machine learning applied to road safety modeling: A systematic literature review. J. Traffic Transp. Eng. (Engl. Ed.) 2020, 7, 775–790. [Google Scholar] [CrossRef]
- Jamal, A.; Zahid, M.; Tauhidur Rahman, M.; Al-Ahmadi, H.M.; Almoshaogeh, M.; Farooq, D.; Ahmad, M. Injury severity prediction of traffic crashes with ensemble machine learning techniques: A comparative study. Int. J. Inj. Control Saf. Promot. 2021, 28, 408–427. [Google Scholar] [CrossRef] [PubMed]
- Iranitalab, A.; Khattak, A. Comparison of four statistical and machine learning methods for crash severity prediction. Accid. Anal. Prev. 2017, 108, 27–36. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Liu, C.; Ding, L. Impact of pavement conditions on crash severity. Accid. Anal. Prev. 2013, 59, 399–406. [Google Scholar] [CrossRef] [PubMed]
- Martensen, H.; Dupont, E. Comparing single vehicle and multivehicle fatal road crashes: A joint analysis of road conditions, time variables and driver characteristics. Accid. Anal. Prev. 2013, 60, 466–471. [Google Scholar] [CrossRef] [PubMed]
- Hosseinpour, M.; Yahaya, A.S.; Sadullah, A.F. Exploring the effects of roadway characteristics on the frequency and severity of head-on crashes: Case studies from Malaysian Federal Roads. Accid. Anal. Prev. 2014, 62, 209–222. [Google Scholar] [CrossRef] [PubMed]
- Yasmin, S.; Eluru, N.; Bhat, C.R.; Tay, R. A latent segmentation based generalized ordered logit model to examine factors influencing driver injury severity. Anal. Methods Accid. Res. 2014, 1, 23–38. [Google Scholar] [CrossRef]
- Rezapour, M.; Moomen, M.; Ksaibati, K. Ordered logistic models of influencing factors on crash injury severity of single and multiple-vehicle downgrade crashes: A case study in Wyoming. J. Saf. Res. 2019, 68, 107–118. [Google Scholar] [CrossRef] [PubMed]
- ANSR. Manual de Prenchimento. Boletim Estatístico de Acidente de Viação. 2013. Available online: http://www.ansr.pt/Estatisticas/BEAV/Documents/MANUALPREENCHIMENTOBEAV.pdf (accessed on 25 January 2022).
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013; Volume 398. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1993. [Google Scholar]
- Research, R. Is See5/C5.0 Better Than C4.5? 2017. Available online: https://rulequest.com/see5-comparison.html (accessed on 25 January 2022).
- He, H.; Garcia, E.A. Learning from Imbalanced Data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2021. [Google Scholar]
- Fiorentini, N.; Losa, M. Handling Imbalanced Data in Road Crash Severity Prediction by Machine Learning Algorithms. Infrastructures 2020, 5, 61. [Google Scholar] [CrossRef]
| Variable | Coefficient | Std. Error | p-Value |
|---|---|---|---|
| Constant | −4.30 | 0.20 | <0.001 |
| Municipality (ref: Alcochete/Almada/Barreiro/Montijo/Setúbal/Sines) | |||
| Alcácer do Sal/Grândola/Moita/Palmela/Santiago do Cacém/Sesimbra/Seixal | 0.18 | 0.04 | <0.01 |
| Accident location (ref: Inside urban area) | |||
| Outside urban area | 0.37 | 0.05 | <0.001 |
| Type of accident (ref: Collision) | |||
| Pedestrian running over | −0.78 | 0.43 | 0.068 |
| Crash | 1.00 | 0.12 | <0.001 |
| Type of road (ref: AE/bridge) | |||
| EN | −0.10 | 0.08 | 0.220 |
| IC/IP | −0.10 | 0.10 | 0.293 |
| Other | −0.74 | 0.09 | <0.001 |
| Accident escape (ref: No) | |||
| Yes | −1.44 | 0.10 | 0.001 |
| Wind velocity m/s | −0.06 | 0.02 | 0.001 |
| Month (ref: November to May) | |||
| June to October | 0.14 | 0.04 | <0.001 |
| Day of the Week (ref: Monday to Thursday) | |||
| Friday to Sunday | 0.07 | 0.04 | 0.045 |
| Hour of the day (ref: 11 p.m.–1 a.m. and 6 a.m.–7 a.m.) | |||
| 1 a.m.–4 a.m. and 7 a.m.–11 p.m. | −0.29 | 0.07 | <0.001 |
| 4 a.m.–5 a.m. | 0.39 | 0.20 | 0.0452 |
| 5 a.m.–6 a.m. | −0.75 | 0.22 | 0.001 |
| Type of vehicle (ref: Light passenger vehicles) | |||
| Motorbikes but not heavy vehicles | 2.68 | 0.05 | <0.001 |
| Heavy vehicles | 0.05 | 0.01 | 0.460 |
| % of male drivers (ref: <50%) | |||
| ≥50% | −0.23 | 0.05 | <0.001 |
| Median age of vehicle | 0.03 | <0.01 | <0.001 |
| Total number of drivers (transf.) | 2.05 | 0.11 | <0.001 |
| Maximum age of drivers (transf. 1) | 4.59 | 0.99 | <0.001 |
| Maximum age of drivers (transf. 2) | 2.02 | 0.24 | <0.001 |
| Type of accident × Type of road | |||
| Pedestrian running over × EN | 2.83 | 0.46 | <0.001 |
| Crash × EN | 0.65 | 0.13 | <0.001 |
| Pedestrian running over × IC/IP | 1.89 | 0.53 | <0.001 |
| Crash × IC/IP | 0.26 | 0.17 | 0.132 |
| Pedestrian running over × Others | 5.20 | 0.44 | <0.001 |
| Crash × Others | 0.87 | 0.12 | <0.001 |
| Measure | Logistic Regression | Machine-Learning Algorithms | ||||
|---|---|---|---|---|---|---|
| Random Forest | Naive Bayes | C5.0 | SVM | KNN | ||
| Accuracy | 0.652 | 0.502 | 0.500 | 0.094 | 0.512 | 0.420 |
| Sensitivity | 0.732 | 0.695 | 0.638 | 0.000 | 0.605 | 0.638 |
| Specificity | 0.645 | 0.482 | 0.486 | 1.000 | 0.502 | 0.398 |
| PPV 1 | 0.171 | 0.122 | 0.114 | - | 0.112 | 0.099 |
| NPV 2 | 0.960 | 0.938 | 0.928 | 0.094 | 0.925 | 0.914 |
| G-mean | 0.687 | 0.579 | 0.557 | 0.000 | 0.551 | 0.504 |
| F-score | 0.277 | 0.208 | 0.193 | - | 0.189 | 0.171 |
| MCC | 0.222 | 0.103 | 0.073 | - | 0.062 | 0.021 |
| Variable | Coefficient | Std. Error | p-Value |
|---|---|---|---|
| Constant | −4.95 | 0.30 | <0.001 |
| Municipality (ref: Alcácer do Sal/Alcochete/Palmela) | |||
| Almada/Moita/Montijo/Sesimbra/Setúbal | −0.67 | 0.12 | <0.001 |
| Barreiro/Grândola/Santiago do Cacém/Seixal/Sines | −0.23 | 0.12 | 0.044 |
| Accident location (ref: Inside urban area) | |||
| Outside urban area | 1.09 | 0.20 | <0.001 |
| Type of accident (ref: Collision) | |||
| Pedestrian running over | 1.61 | 0.19 | <0.001 |
| Crash | 0.80 | 0.16 | <0.001 |
| Type of roadside (ref: Paved) | |||
| Unpaved or non-existent | 0.61 | 0.16 | <0.001 |
| Type of road (ref: AE/bridge or other) | |||
| IC/IP or EN | 0.50 | 0.11 | <0.001 |
| Type of lane (ref: Without central separator) | |||
| With central separator | −0.52 | 0.16 | 0.001 |
| Day of the week (ref: Thursday to Monday) | |||
| Tuesday and Wednesday | −0.25 | 0.11 | 0.024 |
| Hour of the day (ref: 8 a.m.–8 p.m.) | |||
| 8 p.m.–2 a.m., 5 a.m.–6 a.m., 7 a.m.–8 a.m. | 0.61 | 0.11 | <0.001 |
| 2 a.m.–5 a.m., 6 a.m.–7 a.m. | 1.11 | 0.19 | <0.001 |
| Type of vehicle (ref: Light passenger vehicles) | |||
| Motorbikes but not heavy vehicles | 1.26 | 0.14 | <0.001 |
| Heavy vehicles | 1.39 | 0.20 | <0.001 |
| % of male drivers (ref: <50%) | |||
| ≥50% | 0.84 | 0.17 | <0.001 |
| Median age of vehicle | 0.02 | 0.01 | 0.009 |
| Maximum victims age | 0.02 | 0.00 | <0.001 |
| Age of the youngest driver | −0.01 | 0.00 | <0.001 |
| Type of accident × Type of vehicle | |||
| Pedestrian running over × motorbikes but not heavy vehicles | −1.45 | 0.61 | 0.017 |
| Crash × motorbikes but not heavy vehicles | −1.08 | 0.23 | <0.001 |
| Pedestrian running over × heavy vehicles | −0.25 | 0.57 | 0.653 |
| Crash × heavy vehicles | −1.86 | 0.57 | 0.001 |
| Type of roadside × Accident location | |||
| Unpaved or non-existent × outside urban area | −0.70 | 0.22 | 0.001 |
| Measure | Logistic Regression | Machine-Learning Algorithms | ||||
|---|---|---|---|---|---|---|
| Random Forest | Naive Bayes | C5.0 | SVM | KNN | ||
| Accuracy | 0.626 | 0.626 | 0.653 | 0.610 | 0.649 | 0.644 |
| Sensitivity | 0.864 | 0.850 | 0.768 | 0.888 | 0.772 | 0.719 |
| Specificity | 0.557 | 0.560 | 0.619 | 0.528 | 0.612 | 0.622 |
| PPV 1 | 0.363 | 0.362 | 0.372 | 0.356 | 0.369 | 0.358 |
| NPV 2 | 0.933 | 0.927 | 0.901 | 0.941 | 0.902 | 0.883 |
| G-mean | 0.694 | 0.690 | 0.690 | 0.685 | 0.688 | 0.669 |
| F-score | 0.511 | 0.508 | 0.501 | 0.508 | 0.499 | 0.478 |
| MCC | 0.353 | 0.344 | 0.325 | 0.351 | 0.322 | 0.289 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Infante, P.; Jacinto, G.; Afonso, A.; Rego, L.; Nogueira, V.; Quaresma, P.; Saias, J.; Santos, D.; Nogueira, P.; Silva, M.; et al. Comparison of Statistical and Machine-Learning Models on Road Traffic Accident Severity Classification. Computers 2022, 11, 80. https://doi.org/10.3390/computers11050080
Infante P, Jacinto G, Afonso A, Rego L, Nogueira V, Quaresma P, Saias J, Santos D, Nogueira P, Silva M, et al. Comparison of Statistical and Machine-Learning Models on Road Traffic Accident Severity Classification. Computers. 2022; 11(5):80. https://doi.org/10.3390/computers11050080
Chicago/Turabian StyleInfante, Paulo, Gonçalo Jacinto, Anabela Afonso, Leonor Rego, Vitor Nogueira, Paulo Quaresma, José Saias, Daniel Santos, Pedro Nogueira, Marcelo Silva, and et al. 2022. "Comparison of Statistical and Machine-Learning Models on Road Traffic Accident Severity Classification" Computers 11, no. 5: 80. https://doi.org/10.3390/computers11050080
APA StyleInfante, P., Jacinto, G., Afonso, A., Rego, L., Nogueira, V., Quaresma, P., Saias, J., Santos, D., Nogueira, P., Silva, M., Costa, R. P., Gois, P., & Manuel, P. R. (2022). Comparison of Statistical and Machine-Learning Models on Road Traffic Accident Severity Classification. Computers, 11(5), 80. https://doi.org/10.3390/computers11050080