A New Development of FDOSM Based on a 2-Tuple Fuzzy Environment: Evaluation and Benchmark of Network Protocols as a Case Study
Abstract
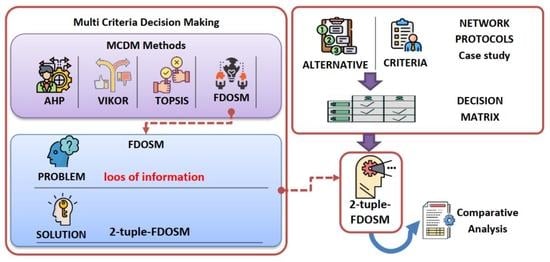
:1. Introduction
2. Related Work
- Step 1: Create the decision matrix.
- Step 2: Select the ideal solution for each criterion (the ideal solution is one of the following: min, max, or critical value).
- Step 3: Create a reference comparison between the ideal solution and other values per criterion, according to the decision-maker’s opinion, to create the opinion matrix.
- Step 4: Convert the opinion matrix into triangular fuzzy numbers (TFNs).
- Step 5: Direct aggregation with the arithmetic mean.
- Step 6: Make the final decision (the lowest is the best).
3. Methodology
3.1. Development 2-Tuple-FDOSM
3.1.1. Data-Transformation Unit
3.1.2. Data-Processing Unit
4. Case Study
5. Results and Discussion
5.1. The Result of the Opinion Matrix
5.2. The Final Rank
6. Comparative Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Opricovic, S.; Tzeng, G.-H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Çelen, A. Comparative Analysis of Normalization Procedures in TOPSIS Method: With an Application to Turkish Deposit Banking Market. Informatica 2014, 25, 185–208. [Google Scholar] [CrossRef] [Green Version]
- Kornyshova, E.; Salinesi, C. MCDM techniques selection approaches: State of the art. In Proceedings of the 2007 IEEE Symposium on Computational Intelligence in Multi-Criteria Decision-Making, Honolulu, HI, USA, 1–5 April 2007. [Google Scholar]
- Zughoul, O.; Zaidan, A.A.; Zaidan, B.B.; Albahri, O.S.; Alazab, M.; Amomeni, U.; Albahri, A.S.; Salih, M.M.; Mohammed, R.T.; Mohammed, K.I.; et al. Novel triplex procedure for ranking the ability of software engineering students based on two levels of AHP and group TOPSIS techniques. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 67–135. [Google Scholar] [CrossRef]
- Zaidan, A.; Zaidan, B.; Hussain, M.; Al-Haiqi, A.; Kiah, M.M.; Abdulnabi, M. Multi-criteria analysis for OS-EMR software selection problem: A comparative study. Decis. Support Syst. 2015, 78, 15–27. [Google Scholar] [CrossRef]
- Abdullateef, B.N.; Elias, N.F.; Mohamed, H.; Zaidan, A.A.; Zaidan, B.B. An evaluation and selection problems of OSS-LMS packages. SpringerPlus 2016, 5, 248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Campanella, G.; Ribeiro, R.A. A framework for dynamic multiple-criteria decision making. Decis. Support Syst. 2011, 52, 52–60. [Google Scholar] [CrossRef]
- Mahdavi, I.; Mahdavi-Amiri, N.; Heidarzade, A.; Nourifar, R. Designing a model of fuzzy TOPSIS in multiple criteria decision making. Appl. Math. Comput. 2008, 206, 607–617. [Google Scholar] [CrossRef]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Mahjouri, M.; Ishak, M.B.; Torabian, A.; Abd Manaf, L.; Halimoon, N.; Ghoddusi, J. Optimal selection of Iron and Steel wastewater treatment technology using integrated multi-criteria deci-sion-making techniques and fuzzy logic. Process Saf. Environ. Prot. 2017, 107, 54–68. [Google Scholar] [CrossRef]
- Abdulkareem, K.H.; Arbaiy, N.; Zaidan, A.A.; Zaidan, B.B.; Albahri, O.S.; Alsalem, M.A.; Salih, M.M. A Novel Multi-Perspective Benchmarking Framework for Selecting Image Dehazing Intelligent Algorithms Based on BWM and Group VIKOR Techniques. Int. J. Inf. Technol. Decis. Mak. 2020, 19, 909–957. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Decision Making with the Analytic Network Process; Springer Science and Business Media LLC.: Berlin, Germany, 2006; Volume 282. [Google Scholar]
- Saaty, T.L. What is the analytic hierarchy process? In Mathematical Models for Decision Support; Springer: Berlin, Germany, 1988; pp. 109–121. [Google Scholar]
- Rezaei, J. Best-worst multi-criteria decision-making method. Omega 2015, 53, 49–57. [Google Scholar] [CrossRef]
- Guo, S.; Zhou, K.; Cao, B.; Yang, C. Combination weights and TOP SIS method for performance evaluation of aluminum electrolysis. In Proceedings of the 2015 Chinese Automation Congress (CAC), Wuhan, China, 27–29 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Sun, R.; Zhang, B.; Liu, T. Ranking web service for high quality by applying improved Entropy-TOPSIS method. In Proceedings of the 2016 17th IEEE/ACIS International Conference on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Shangai, China, 30 May–1 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 249–254. [Google Scholar]
- Wang, X.; Peng, B. Determining the value of the port transport waters: Based on improved TOPSIS model by multiple regression weighting. Ocean Coast. Manag. 2015, 107, 37–45. [Google Scholar] [CrossRef]
- Huang, X.; Feng, S. Research on the teaching quality evaluation for the physical education in colleges based on the AHPTOPSIS. Chem. Eng. Trans. 2015, 46, 487–492. [Google Scholar]
- Keshtkar, A.R.; Oros, Z.; Mohammadkhan, S.; Eagdari, S.; Paktinat, H. Multi-criteria analysis in Artemia farming site selection for sustainable desert ecosystems planning and management (case study: Siahkouh Playa, Iran). Environ. Earth Sci. 2016, 75, 1195. [Google Scholar] [CrossRef]
- Koczkodaj, W.; Urban, R. Axiomatization of inconsistency indicators for pairwise comparisons. Int. J. Approx. Reason. 2018, 94, 18–29. [Google Scholar] [CrossRef] [Green Version]
- Destercke, S. A generic framework to include belief functions in preference handling and multi-criteria decision. Int. J. Approx. Reason. 2018, 98, 62–77. [Google Scholar] [CrossRef] [Green Version]
- Benítez, J.; Izquierdo, J.; Pérez-García, R.; Ramos-Martínez, E. A simple formula to find the closest consistent matrix to a reciprocal matrix. Appl. Math. Model. 2014, 38, 3968–3974. [Google Scholar] [CrossRef]
- Morgan, R. An investigation of constraints upon fisheries diversification using the Analytic Hierarchy Process (AHP). Mar. Policy 2017, 86, 24–30. [Google Scholar] [CrossRef]
- Wu, J.-Z.; Tiao, P.-J. A validation scheme for intelligent and effective multiple criteria decision-making. Appl. Soft Comput. 2018, 68, 866–872. [Google Scholar] [CrossRef]
- Vahdani, B.; Tavakkoli-Moghaddam, R.; Mousavi, S.M.; Ghodratnama, A. Soft computing based on new interval-valued fuzzy modified multi-criteria decision-making method. Appl. Soft Comput. 2013, 13, 165–172. [Google Scholar] [CrossRef]
- Xu, Z.; Zhang, X. Hesitant fuzzy multi-attribute decision making based on TOPSIS with incomplete weight information. Knowl.-Based Syst. 2013, 52, 53–64. [Google Scholar] [CrossRef]
- Salih, M.; Zaidan, B.; Zaidan, A.; Ahmed, M. Survey on fuzzy TOPSIS state-of-the-art between 2007 and 2017. Comput. Oper. Res. 2018, 104, 207–227. [Google Scholar] [CrossRef]
- Singh, R.K.; Benyoucef, L. A fuzzy TOPSIS based approach for e-sourcing. Eng. Appl. Artif. Intell. 2011, 24, 437–448. [Google Scholar] [CrossRef]
- Nădăban, S.; Dzitac, S.; Dzitac, I. Fuzzy TOPSIS: A General View. Procedia Comput. Sci. 2016, 91, 823–831. [Google Scholar] [CrossRef] [Green Version]
- Salih, M.M.; Albahri, O.S.; Zaidan, A.A.; Zaidan, B.B.; Jumaah, F.M. Benchmarking of AQM methods of network congestion control based on extension of interval type-2 trapezoidal fuzzy decision by opinion score method. Telecommun. Syst. 2021, 77, 493–522. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, S.; Barman, A.G. Supplier selection using fuzzy TOPSIS multi criteria model for a small scale steel manufacturing unit. Procedia Comput. Sci. 2018, 133, 905–912. [Google Scholar] [CrossRef]
- Yaakob, A.M.; Serguieva, A.; Gegov, A. FN-TOPSIS: Fuzzy Networks for Ranking Traded Equities. IEEE Trans. Fuzzy Syst. 2016, 25, 315–332. [Google Scholar] [CrossRef] [Green Version]
- Salih, M.M.; Zaidan, B.; Zaidan, A. Fuzzy decision by opinion score method. Appl. Soft Comput. 2020, 96, 106595. [Google Scholar] [CrossRef]
- Albahri, O.S.; Zaidan, A.A.; Salih, M.M.; Zaidan, B.B.; Khatari, M.A.; Ahmed, M.A.; Albahri, A.S.; Alazab, M. Multidimensional benchmarking of the active queue management methods of network congestion control based on extension of fuzzy decision by opinion score method. Int. J. Intell. Syst. 2020, 36, 796–831. [Google Scholar] [CrossRef]
- Albahri, A.; Zaidan, A.; Alnoor, A.; Alsattar, H.; Mohammed, R.; Alamoodi, A.; Zaidan, B.; Aickelin, U.; Alazab, M.; Garfan, S.; et al. Integration of fuzzy-weighted zero-inconsistency and fuzzy decision by opinion score methods under a q-rung orthopair environment: A distribution case study of COVID-19 vaccine doses. Comput. Stand. Interfaces 2021, 80, 103572. [Google Scholar] [CrossRef]
- Albahri, O.; Zaidan, A.; Alsattar, H.; Mohammed, R.; Aickelin, U.; Kou, G.; Jumaah, F.; Salih, M.M.; Alamoodi, A.; Zaidan, B.; et al. Novel dynamic fuzzy Decision-Making framework for COVID-19 vaccine dose recipients. J. Adv. Res. 2021, 37, 147–168. [Google Scholar] [CrossRef]
- Alsalem, M.; Alsattar, H.; Albahri, A.; Mohammed, R.; Zaidan, A.; Alnoor, A.; Alamoodi, A.; Qahtan, S.; Zaidan, B.; Aickelin, U.; et al. Based on T-spherical fuzzy environment: A combination of FWZIC and FDOSM for prioritising COVID-19 vaccine dose recipients. J. Infect. Public Health 2021, 14, 1513–1559. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, U.S.; Albahri, A.S.; AlSattar, H.A.; Zaidan, A.A.; Talal, M.; Mohammed, R.A.; Albahri, O.S.; Zaidan, B.B.; Alamoodi, A.H.; Hadi, S.M. A Methodology of DASs Benchmarking to Support Industrial Community Characteristics in Designing and Implementing Advanced Driver Assistance Systems Within Vehicles. 2021. Available online: https://assets.researchsquare.com/files/rs-875230/v1_covered.pdf?c=1632176242 (accessed on 1 May 2022).
- Al-Samarraay, M.S.; Salih, M.M.; Ahmed, M.A.; Zaidan, A.A.; Albahri, O.S.; Pamucar, D.; AlSattar, H.A.; Alamoodi, A.H.; Zaidan, B.B.; Dawood, K.; et al. A new extension of FDOSM based on Pythagorean fuzzy environment for evaluating and benchmarking sign language recognition systems. Neural Comput. Appl. 2022, 34, 4937–4955. [Google Scholar] [CrossRef]
- Al-Samarraay, M.S.; Zaidan, A.A.; Albahri, O.S.; Pamucar, D.; AlSattar, H.A.; Alamoodi, A.H.; Zaidan, B.B.; Albahri, A.S. Extension of interval-valued Pythagorean FDOSM for evaluating and benchmarking real-time SLRSs based on multidimensional criteria of hand gesture recognition and sensor glove perspectives. Appl. Soft Comput. 2021, 116, 108284. [Google Scholar] [CrossRef]
- Salih, M.M.; Al-Qaysi, Z.; Shuwandy, M.L.; Ahmed, M.; Hasan, K.F.; Muhsen, Y.R. A new extension of fuzzy decision by opinion score method based on Fermatean fuzzy: A benchmarking COVID-19 machine learning methods. J. Intell. Fuzzy Syst. 2022; in press. [Google Scholar]
- Herrera, F.; Martínez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Herrera, F.; Martínez, L. A model based on linguistic 2-tuples for dealing with multigranular hierarchical linguistic contexts in multi-expert decision-making. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2001, 31, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Dutta, B.; Guha, D.; Mesiar, R. A Model Based on Linguistic 2-Tuples for Dealing with Heterogeneous Relationship among Attributes in Multi-expert Decision Making. IEEE Trans. Fuzzy Syst. 2014, 23, 1817–1831. [Google Scholar] [CrossRef]
- Zhu, H.; Zhao, J.; Xu, Y. 2-dimension linguistic computational model with 2-tuples for multi-attribute group decision making. Knowl.-Based Syst. 2016, 103, 132–142. [Google Scholar] [CrossRef]
- Jin-Hsien, W.; Jongyun, H. A new version of 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2006, 14, 435–445. [Google Scholar] [CrossRef]
- Delgado, M.; Herrera, F.; Herrera-Viedma, E.; Martin-Bautista, M.J.; Martinez, L.; Vila, M.A. A communication model based on the 2-tuple fuzzy linguistic representation for a distributed intelligent agent system on Internet. Soft Comput. 2002, 6, 320–328. [Google Scholar] [CrossRef]
- Najm, I.A.; Ismail, M.; Lloret, J.; Ghafoor, K.Z.; Zaidan, B.B.; Rahem, A.A.R.T. Improvement of SCTP congestion control in the LTE-A network. J. Netw. Comput. Appl. 2015, 58, 119–129. [Google Scholar] [CrossRef]


| Alternatives | CWND | Throughput | Queue Size | Pkt Loss |
|---|---|---|---|---|
| A1 | 120 | 9,881,687 | 48,424.92 | 209.75 |
| A2 | 130 | 9,912,326 | 56,199.3 | 81.75 |
| A3 | 145 | 9,905,462 | 53,788.4 | 24 |
| A4 | 200 | 10,120,778 | 57,674 | 27 |
| A5 | 205 | 9,902,374 | 51,274.2 | 43.5 |
| A6 | 212 | 10,023,750 | 51,180.7 | 64.5 |
| A7 | 202 | 10,264,182 | 57,581.3 | 70.5 |
| A8 | 225 | 10,106,678 | 52,895.4 | 94.5 |
| A9 | 235 | 20,368,886 | 59,680.9 | 104 |
| The Opinion Matrix of the First Decision-Maker | ||||
|---|---|---|---|---|
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss |
| A1 | Huge Difference | Huge Difference | Huge Difference | Huge Difference |
| A2 | Huge Difference | Big Difference | Slight Difference | Big Difference |
| A3 | Big Difference | Big Difference | Difference | No Difference |
| A4 | Difference | Difference | Slight Difference | Slight Difference |
| A5 | Difference | Big Difference | Big Difference | Difference |
| A6 | Difference | Difference | Big Difference | Difference |
| A7 | Difference | Slight Difference | Slight Difference | Difference |
| A8 | Slight Difference | Slight Difference | Difference | Big Difference |
| A9 | No Difference | No Difference | No Difference | Big Difference |
| The Opinion Matrix of the Second Decision-Maker | ||||
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss |
| A1 | Huge Difference | Slight Difference | No Difference | Huge Difference |
| A2 | Huge Difference | No Difference | Huge Difference | Big Difference |
| A3 | Big Difference | Slight Difference | Big Difference | Slight Difference |
| A4 | No Difference | Difference | Huge Difference | No Difference |
| A5 | Slight Difference | Slight Difference | Difference | Difference |
| A6 | Slight Difference | Difference | Difference | Difference |
| A7 | Slight Difference | Big Difference | Huge Difference | Difference |
| A8 | Difference | Big Difference | Big Difference | Big Difference |
| A9 | Difference | Big Difference | Huge Difference | Big Difference |
| The Opinion Matrix of the Third Decision-Maker | ||||
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss |
| A1 | Huge Difference | Slight Difference | Big Difference | Huge Difference |
| A2 | Huge Difference | Slight Difference | Slight Difference | Big Difference |
| A3 | Huge Difference | Slight Difference | Difference | No Difference |
| A4 | Big Difference | Slight Difference | Slight Difference | No Difference |
| A5 | Big Difference | No Difference | Difference | Slight Difference |
| A6 | Big Difference | Slight Difference | Difference | Difference |
| A7 | Difference | No Difference | Slight Difference | Difference |
| A8 | Slight Difference | No Difference | Difference | Big Difference |
| A9 | No Difference | No Difference | No Difference | Big Difference |
| Decision-Makers | CWND | Throughput | Queue Size | Pkt Loss |
|---|---|---|---|---|
| Decision-maker 1 | 235 | 20,368,886 | 59,680.9 | 24 |
| Decision-maker 2 | 200 | 9,912,326 | 48,424.92 | 27 |
| Decision-maker 3 | 235 | 20,368,886 | 59,680.9 | 27 |
| Linguistic Terms | Fuzzy Numbers |
|---|---|
| No difference | (0, 0.1, 0.3) |
| Slight Difference | (0.1, 0.3, 0.5) |
| Difference | (0.3, 0.5, 0.75) |
| Big Difference | (0.5, 0.75, 0.9) |
| Huge Difference | (0.75, 0.9, 1) |
| The Fuzzy Opinion Matrix for the First Decision-Maker | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss | ||||||||
| A1 | 0.75 | 0.90 | 1.00 | 0.75 | 0.90 | 1.00 | 0.75 | 0.90 | 1.00 | 0.75 | 0.90 | 1.00 |
| A2 | 0.75 | 0.90 | 1.00 | 0.50 | 0.75 | 0.90 | 0.10 | 0.30 | 0.50 | 0.50 | 0.75 | 0.90 |
| A3 | 0.50 | 0.75 | 0.90 | 0.50 | 0.75 | 0.90 | 0.30 | 0.50 | 0.75 | 0.00 | 0.10 | 0.30 |
| A4 | 0.30 | 0.50 | 0.75 | 0.30 | 0.50 | 0.75 | 0.10 | 0.30 | 0.50 | 0.10 | 0.30 | 0.50 |
| A5 | 0.30 | 0.50 | 0.75 | 0.50 | 0.75 | 0.90 | 0.50 | 0.75 | 0.90 | 0.30 | 0.50 | 0.75 |
| A6 | 0.30 | 0.50 | 0.75 | 0.30 | 0.50 | 0.75 | 0.50 | 0.75 | 0.90 | 0.30 | 0.50 | 0.75 |
| A7 | 0.30 | 0.50 | 0.75 | 0.10 | 0.30 | 0.50 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 |
| A8 | 0.10 | 0.30 | 0.50 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 | 0.50 | 0.75 | 0.90 |
| A9 | 0.00 | 0.10 | 0.30 | 0.00 | 0.10 | 0.30 | 0.00 | 0.10 | 0.30 | 0.50 | 0.75 | 0.90 |
| The Fuzzy Opinion Matrix for the Second Decision-Maker | ||||||||||||
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss | ||||||||
| A1 | 0.75 | 0.90 | 1.00 | 0.10 | 0.30 | 0.50 | 0.00 | 0.10 | 0.30 | 0.75 | 0.90 | 1.00 |
| A2 | 0.75 | 0.90 | 1.00 | 0.00 | 0.10 | 0.30 | 0.75 | 0.90 | 1.00 | 0.50 | 0.75 | 0.90 |
| A3 | 0.50 | 0.75 | 0.90 | 0.10 | 0.30 | 0.50 | 0.50 | 0.75 | 0.90 | 0.10 | 0.30 | 0.50 |
| A4 | 0.00 | 0.10 | 0.30 | 0.30 | 0.50 | 0.75 | 0.75 | 0.90 | 1.00 | 0.00 | 0.10 | 0.30 |
| A5 | 0.10 | 0.30 | 0.50 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 | 0.30 | 0.50 | 0.75 |
| A6 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 | 0.30 | 0.50 | 0.75 | 0.30 | 0.50 | 0.75 |
| A7 | 0.10 | 0.30 | 0.50 | 0.50 | 0.75 | 0.90 | 0.75 | 0.90 | 1.00 | 0.30 | 0.50 | 0.75 |
| A8 | 0.30 | 0.50 | 0.75 | 0.50 | 0.75 | 0.90 | 0.50 | 0.75 | 0.90 | 0.50 | 0.75 | 0.90 |
| A9 | 0.30 | 0.50 | 0.75 | 0.50 | 0.75 | 0.90 | 0.75 | 0.90 | 1.00 | 0.50 | 0.75 | 0.90 |
| The Fuzzy Opinion Matrix for the Third Decision-Maker | ||||||||||||
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss | ||||||||
| A1 | 0.75 | 0.90 | 1.00 | 0.10 | 0.30 | 0.50 | 0.50 | 0.75 | 0.90 | 0.75 | 0.90 | 1.00 |
| A2 | 0.75 | 0.90 | 1.00 | 0.10 | 0.30 | 0.50 | 0.10 | 0.30 | 0.50 | 0.50 | 0.75 | 0.90 |
| A3 | 0.75 | 0.90 | 1.00 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 | 0.00 | 0.10 | 0.30 |
| A4 | 0.50 | 0.75 | 0.90 | 0.10 | 0.30 | 0.50 | 0.10 | 0.30 | 0.50 | 0.00 | 0.10 | 0.30 |
| A5 | 0.50 | 0.75 | 0.90 | 0.00 | 0.10 | 0.30 | 0.30 | 0.50 | 0.75 | 0.10 | 0.30 | 0.50 |
| A6 | 0.50 | 0.75 | 0.90 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 | 0.30 | 0.50 | 0.75 |
| A7 | 0.30 | 0.50 | 0.75 | 0.00 | 0.10 | 0.30 | 0.10 | 0.30 | 0.50 | 0.30 | 0.50 | 0.75 |
| A8 | 0.10 | 0.30 | 0.50 | 0.00 | 0.10 | 0.30 | 0.30 | 0.50 | 0.75 | 0.50 | 0.75 | 0.90 |
| A9 | 0.00 | 0.10 | 0.30 | 0.00 | 0.10 | 0.30 | 0.00 | 0.10 | 0.30 | 0.50 | 0.75 | 0.90 |
| Alternatives | CWND | Throughput | Queue Size | Pkt Loss | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | 0.75 | 0.9 | 1 | 0.1 | 0.5 | 1 | 0 | 0.583333 | 1 | 0.75 | 0.9 | 1 |
| A2 | 0.75 | 0.9 | 1 | 0 | 0.383333 | 0.9 | 0.1 | 0.5 | 1 | 0.5 | 0.75 | 0.9 |
| A3 | 0.5 | 0.8 | 1 | 0.1 | 0.45 | 0.9 | 0.3 | 0.583333 | 0.9 | 0 | 0.166667 | 0.5 |
| A4 | 0 | 0.45 | 0.9 | 0.1 | 0.433333 | 0.75 | 0.1 | 0.5 | 1 | 0 | 0.166667 | 0.5 |
| A5 | 0.1 | 0.516667 | 0.9 | 0 | 0.383333 | 0.9 | 0.3 | 0.583333 | 0.9 | 0.1 | 0.433333 | 0.75 |
| A6 | 0.1 | 0.516667 | 0.9 | 0.1 | 0.433333 | 0.75 | 0.3 | 0.583333 | 0.9 | 0.3 | 0.5 | 0.75 |
| A7 | 0.1 | 0.433333 | 0.75 | 0 | 0.383333 | 0.9 | 0.1 | 0.5 | 1 | 0.3 | 0.5 | 0.75 |
| A8 | 0.1 | 0.366667 | 0.75 | 0 | 0.383333 | 0.9 | 0.3 | 0.583333 | 0.9 | 0.5 | 0.75 | 0.9 |
| A9 | 0 | 0.233333 | 0.75 | 0 | 0.316667 | 0.9 | 0 | 0.366667 | 1 | 0.5 | 0.75 | 0.9 |
| Alternatives | Fuzzy Score | 2-Tuple-FDOSM Score | Rank | ||
|---|---|---|---|---|---|
| A1 | 0.4 | 0.720833 | 1 | BD, −0.3 | 9 |
| A2 | 0.3375 | 0.633333 | 0.95 | BD, −0.16 | 8 |
| A3 | 0.225 | 0.5 | 0.825 | DI | 5 |
| A4 | 0.05 | 0.3875 | 0.7875 | SD, 0.08 | 1 |
| A5 | 0.125 | 0.479167 | 0.8625 | DI, −0.3 | 3 |
| A6 | 0.2 | 0.508333 | 0.825 | DI, 0.08 | 6 |
| A7 | 0.125 | 0.454167 | 0.85 | D, −0.5 | 2 |
| A8 | 0.225 | 0.520833 | 0.8625 | DI, 0.2 | 7 |
| A9 | 0.125 | 0.416667 | 0.8875 | DI, −0.09 | 4 |
| Alternatives | Score | Rank |
|---|---|---|
| A1 | 0.7097 | 9 |
| A2 | 0.6194 | 8 |
| A3 | 0.4958 | 5 |
| A4 | 0.3958 | 1 |
| A5 | 0.4806 | 4 |
| A6 | 0.5139 | 6 |
| A7 | 0.4597 | 3 |
| A8 | 0.5139 | 6 |
| A9 | 0.4222 | 2 |
| Alternatives | Score | Rank |
|---|---|---|
| A1 | 0 | 9 |
| A2 | 0.620835 | 7 |
| A3 | 0.799564 | 3 |
| A4 | 0.910848 | 1 |
| A5 | 0.855029 | 2 |
| A6 | 0.772874 | 4 |
| A7 | 0.746926 | 5 |
| A8 | 0.639203 | 6 |
| A9 | 0.604535 | 8 |
| No. | Comparison Issue | 2-Tuple-FDOSM | TOPSIS |
|---|---|---|---|
| 1 | Missing information | √ | × |
| 2 | Immeasurable value | √ | × |
| 3 | Weight | √ | × |
| 4 | Normalization | √ | × |
| 5 | Ideal solution and distance measurement | √ | × |
| 6 | Ambiguous and vague information | √ | √ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maher, R.M.; Salih, M.M.; Hussein, H.A.; Ahmed, M.A. A New Development of FDOSM Based on a 2-Tuple Fuzzy Environment: Evaluation and Benchmark of Network Protocols as a Case Study. Computers 2022, 11, 109. https://doi.org/10.3390/computers11070109
Maher RM, Salih MM, Hussein HA, Ahmed MA. A New Development of FDOSM Based on a 2-Tuple Fuzzy Environment: Evaluation and Benchmark of Network Protocols as a Case Study. Computers. 2022; 11(7):109. https://doi.org/10.3390/computers11070109
Chicago/Turabian StyleMaher, Rand M., Mahmood M. Salih, Harith A. Hussein, and Mohamed A. Ahmed. 2022. "A New Development of FDOSM Based on a 2-Tuple Fuzzy Environment: Evaluation and Benchmark of Network Protocols as a Case Study" Computers 11, no. 7: 109. https://doi.org/10.3390/computers11070109
APA StyleMaher, R. M., Salih, M. M., Hussein, H. A., & Ahmed, M. A. (2022). A New Development of FDOSM Based on a 2-Tuple Fuzzy Environment: Evaluation and Benchmark of Network Protocols as a Case Study. Computers, 11(7), 109. https://doi.org/10.3390/computers11070109