Optimization of Nano-Process Deposition Parameters Based on Gravitational Search Algorithm
Abstract
:1. Introduction
2. Problem Formulation
3. Brief Reviews
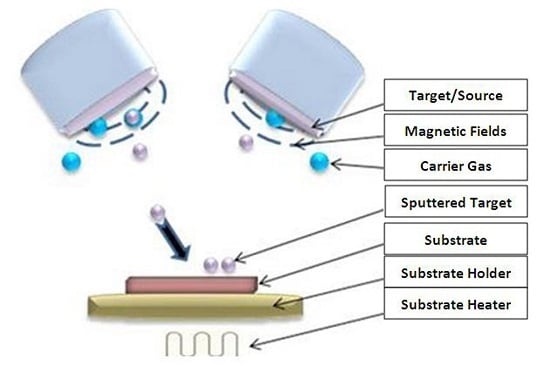
3.1. RF Magnetron Sputtering Process
3.2. Optimization of Sputtering Process Parameters Based on Computational Intelligence Techniques
4. Proposed Methodology
4.1. Experimental Data
4.2. GSA Optimization
5. Results and Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| GSA | Gravitational Search Algorithm |
| GA | Genetic Algorithm |
| PSO | Particle Swarm Optimization |
| ACO | Ant Colony Optimization |
| AIS | Artificial Immune System |
| AFSA | Artificial Fish Swarm Algorithm |
References
- Bhat, J.S. Concerns of New Technology Based Industries—The Case of Nanotechnology. Technovation 2003, 25, 457–462. [Google Scholar] [CrossRef]
- Fernandez, S.; Naranjo, F.B. Optimization of Aluminum-doped Zinc Oxide Films Deposited at Low Temperature by Radio-Frequency Sputtering on Flexible Substrates for Solar Cell Applications. Sol. Energy Mater. Sol. Cells 2010, 94, 157–163. [Google Scholar] [CrossRef]
- Ho, W.; Tsai, J.; Hsu, G. Process Parameters Optimization: A Design Study for TiO Thin Film of Vacuum Sputtering Process. IEEE Trans. Autom. Sci. Eng. 2010, 7, 143–146. [Google Scholar] [CrossRef]
- Norlina, M.S.; Mazidah, P.; Sin, N.D.M.; Rusop, M. Computational Intelligence Technique in Optimization of Nano-process Deposition Parameters. In Proceedings of the 2015 7th Computer Science and Electronic Engineering Conference, Colchester, UK, 24–25 September 2015.
- Ath, M.U.; Jarrah, I.; Syukor, A.; Jaya, M.; Asyadi, M. Intelligence integration of particle swarm optimization and physical vapour deposition for tin grain size coating process parameters. J. Theor. Appl. Inf. Technol. 2016, 84, 355–369. [Google Scholar]
- Shams, M.; Rashedi, E.; Hakimi, A. Clustered-gravitational search algorithm and its application in parameter optimization of a low noise amplifier. Appl. Math. Comput. 2015, 258, 436–453. [Google Scholar] [CrossRef]
- De Moura Oliveira, P.B.; Solteiro Pires, E.J.; Novais, P. Design of Posicast PID control systems using a gravitational search algorithm. Neurocomputing 2015, 167, 18–23. [Google Scholar] [CrossRef]
- Saiful, M.; Aziz, I.; Wahyudi, S.; Sudin, S.; Abdul, N.; Faramarzi, M. Gravitational Search Algorithm Optimization for PID Controller Tuning in Waste-water Treatment Process. J. Teknol. 2015, 73, 103–109. [Google Scholar] [CrossRef]
- Islam, S.M. Gravitational Search Algorithm Applied to Optimal Power Flow Problem. Int. J. Emerg. Res. Manag. Technol. 2015, 4, 120–127. [Google Scholar]
- Sarafrazi, S.; Nezamabadi-pour, H. Facing the classification of binary problems with a GSA-SVM hybrid system. Math. Comput. Model. 2013, 57, 270–278. [Google Scholar] [CrossRef]
- Beheshti, Z.; Mariyam, S.; Shamsuddin, H. A Review of Population-based Meta-Heuristic Algorithm. Int. J. Adv. Soft Comput. 2013, 5, 1–35. [Google Scholar]
- Khadanga, R.K.; Panda, S. Gravitational search algorithm for Unified Power Flow Controller based damping controller design. In Proceedings of the International Conference on Energy, Automation and Signal, Bhubaneswar, India, 28–30 December 2011.
- Lin, H.-C.; Su, C.-T.; Wang, C.-C.; Chang, B.-H.; Juang, R.-C. Parameter Optimization of Continuous Sputtering Process based on Taguchi Methods, Neural Networks, Desirability Function and Genetic Algorithms. Expert Syst. Appl. 2012, 39, 12918–12925. [Google Scholar] [CrossRef]
- Derringer, G.; Suich, R. Simultaneous Optimization of Several Response Variables. J. Qual. Technol. 1980, 12, 2–7. [Google Scholar]
- Yang, P.; Ren, C.S.; Wang, D.Z.; Qi, X.L.; Guo, S.H.; Ma, T.C. Influence of Additional Magnetic Field on Plasma Parameters in Magnetron Sputtering. Vacuum 2009, 83, 1376–1381. [Google Scholar] [CrossRef]
- Sivapragash, M.; Kumaradhas, P.; Retnam, B.S.J.; Joseph, X.F.; Pillai, U.T.S. Taguchi based genetic approach for optimizing the PVD process parameter for coating ZrN on AZ91D magnesium alloy. Mater. Des. 2016, 90, 713–722. [Google Scholar] [CrossRef]
- Jarrah, M.I.; Jaya, A.S.M.; Muhamad, M.R.; Rahman, M.N.A.; Basari, A.S. Modeling and Optimization of Physical Vapour Deposition Coating Process Parameters For TiN Grain Size Using Combined Genetic Algorithms With Response Surface Methodology. J. Theor. Appl. Inf. Technol. 2015, 77, 235–253. [Google Scholar]
- Cho, E.N.; Moon, P.; Kim, C.E.; Yun, I. Modeling and optimization of ITO/Al/ITO multilayer films characteristics using neural network and genetic algorithm. Expert Syst. Appl. 2012, 39, 8885–8889. [Google Scholar] [CrossRef]
- Kim, C.E.; Moon, P.; Yun, I.; Kim, S.; Myoung, J.-M.; Jang, H.W.; Bang, J. Process estimation and optimized recipes of ZnO:Ga thin film characteristics for transparent electrode applications. Expert Syst. Appl. 2011, 38, 2823–2827. [Google Scholar] [CrossRef]
- Veriansyah, B.; Kim, J.-D.; Min, B.K.; Shin, Y.H.; Lee, Y.-W.; Kim, J. Continuous Synthesis of Surface-Modified Zinc Oxide Nanoparticles in Supercritical Methanol. J. Supercrit. Fluids 2010, 52, 76–83. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Sabri, N.M.; Puteh, M.; Mahmood, M.R. A Review of Gravitational Search Algorithm. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–39. [Google Scholar]
- Mirjalili, S.; Hashim, S.Z.M.; Moradian Sardroudi, H. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput. 2012, 218, 11125–11137. [Google Scholar] [CrossRef]
- Shrivastri, S.; Deshmukh, R. Data Classification Particle Swarm Optimization and Gravitational Search Algorithm. Int. J. Innov. Res. Sci. Eng. Technol. 2014, 3, 9734–9741. [Google Scholar]
- Davarynejad, M.; Van Den Berg, J.; Rezaei, J. Evaluating center-seeking and initialization bias: The case of particle swarm and gravitational search algorithms. Inf. Sci. 2014, 278, 802–821. [Google Scholar] [CrossRef]
- Kim, B.; Lee, S.; Min, C.; Kim, T. Optimization of transmittance characteristic of indium tin oxide film using neural networks. Met. Mater. Int. 2010, 16, 793–797. [Google Scholar] [CrossRef]
- Yeh, C.-W.; Wu, K.-R. Neural network-based system for optimizing process parameters of semiconductor compounds. In Proceedings of the 2nd IEEE International Conference on Information Management and Engineering, Chengdu, China, 16–18 April 2010.
- Tsai, J.-T.; Ho, W.-H.; Hsu, G.-M.; Liu, T.-K.; Chou, J.-H. Optimal Process Design Using Soft Computing Approaches. In Proceedings of the SICE Annual Conference 2008, Tokyo, Japan, 20–22 August 2008.
- Braun, C.E.; Chiwiacowsky, L.D.; Arthur, T.G. Variations of Ant Colony Optimization for the solution of the structural damage identification problem. Procedia Comput. Sci. 2015, 51, 875–884. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, W.; Wang, B.; Chen, X. Intelligent fault diagnosis of rotating machinery using support vector machine with ant colony algorithm for synchronous feature selection and parameter optimization. Neurocomputing 2015, 167, 260–279. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; He, C.; Tang, C.; Zhou, J. RFID reader-to-reader collision avoidance model with multiple-density tag distribution solved by artificial immune network optimization. Appl. Soft Comput. 2015, 30, 249–264. [Google Scholar] [CrossRef]
- Souza, S.S.F.; Romero, R.; Franco, J.F. Artificial immune networks Copt-aiNet and Opt-aiNet applied to the reconfiguration problem of radial electrical distribution systems. Electr. Power Syst. Res. 2015, 119, 304–312. [Google Scholar] [CrossRef]




| No | Deposition Parameter | Lower Bound (L) | Upper Bound (U) | Target (T) |
|---|---|---|---|---|
| 1 | RF power (watt) | 10 | 450 | 200 |
| 2 | Deposition time (min) | 1 | 240 | 60 |
| 3 | Oxygen flow rate (sccm) | 0 | 100 | - |
| 4 | Argon flow rate (sccm) | 1 | 100 | - |
| 5 | Substrate temperature (°C) | 25 | 500 | - |
| 6 | Working pressure (mTorr) | 1 | 50 | - |
| No. | Constraints |
|---|---|
| 1 | 10 ≤ power (watt) ≤ 450 |
| 2 | 1 ≤ time (min) ≤ 240 |
| 3 | 0 ≤ oxygen (sccm) ≤ 100 |
| 4 | 1 ≤ argon (sccm) ≤ 100 |
| 5 | 25 ≤ temperature (°C) ≤ 500 |
| 6 | 1 ≤ pressure (mTorr) ≤ 50 |
| Process Type | Technique | Parameters | Material | Result | Ref. |
|---|---|---|---|---|---|
| PVD process | GA, Taguchi | (1) Gas (2) Chamber pressure (3) Power input | Zirconium nitride (ZrN) | Achieve higher coating performance. | [16] |
| PVD Magnetron Sputtering | PSO | (1) Nitrogen pressure (2) Argon pressure (3) Turntable Speed | Titanium nitrite (TiN) | Acceptable performance | [5] |
| Unbalanced magnetron sputtering | GA | (1) Nitrogen pressure (2) Argon pressure (3) TurntableSpeed | Titanium Nitride (TiN) | Reduce the minimum value of coating layer grain size feature. | [17] |
| Roll-to-roll continuous sputtering | ANN, GA, Taguchi, desirability function | (1) Chamber pressure (2) Sputtering power (3) Nitrogen flow rate (4) Process line speed | Not stated | Performance is better than traditional approach. | [13] |
| DC magnetron sputtering | ANN, GA | (1) Thin film thickness (2) Annealing temperature | Indium thin oxide (ITO) and Aluminium (Al) | Results were well matched with the measured data. | [18] |
| RF magnetron sputtering | ANN, GA | (1) Thin film thickness (2) Annealing temperature | Ga-doped zinc oxide (ZnO:Ga) | Effective method to predict the desired process condition. | [19] |
| Deposition Parameters | Ranges |
|---|---|
| RF power (watt) | 50–500 |
| Deposition time (min) | 15–240 |
| Oxygen flow rate (sccm) | 0–100 |
| Argon flow rate (sccm) | 1–100 |
| Substrate temperature (°C) | 20–500 |
| Working pressure (mTorr) | 1–50 |
| Parameter | Value |
|---|---|
| Number of agents | 100 |
| Gravitational constant, G | 10 |
| Alpha, α | 15 |
| Epsilon | 0.0001 |
| Iterations | 200 |
| Technique | Fitness Values of Optimized Parameter Combination | Processing Times (s) | |||
|---|---|---|---|---|---|
| Min | Mean | Max | σ | Mean | |
| GSA | 0.8871 | 0.8871 | 0.8871 | 0.0000 | 5.466 |
| PSO | 0.354 | 0.6473 | 0.847 | 0.1642 | 0.350 |
| GA | 0.8071 | 0.8657 | 0.8701 | 0.0315 | 0.726 |
| AIS | 0.0000 | 0.4721 | 0.8489 | 0.3525 | 0.484 |
| ACO | 0.5553 | 0.5553 | 0.5553 | 0.0000 | 0.634 |
| - | Actual Laboratory Experiment Results | ||||
|---|---|---|---|---|---|
| GSA | PSO | GA | AIS | ACO | |
| Most optimized parameter combination | (200, 60, 0, 45, 500, 7) | (200, 60, 5, 45, 400, 7) | (200, 59, 0, 45, 485, 7) | (200, 60, 5, 45, 500, 7) | (50, 60, 5, 45, 200, 7) |
| Fitness value | 0.8871 | 0.847 | 0.8701 | 0.8489 | 0.5553 |
| Conductivity (Sm−1) | 13.2 | 5.46 | 7.68 | 5.78 | 0.00128 |
| Optical band gap energy (eV) | 3.28 | 3.12 | 3.24 | 3.31 | 3.24 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohd Sabri, N.; Md Sin, N.D.; Puteh, M.; Mahmood, M.R. Optimization of Nano-Process Deposition Parameters Based on Gravitational Search Algorithm. Computers 2016, 5, 12. https://doi.org/10.3390/computers5020012
Mohd Sabri N, Md Sin ND, Puteh M, Mahmood MR. Optimization of Nano-Process Deposition Parameters Based on Gravitational Search Algorithm. Computers. 2016; 5(2):12. https://doi.org/10.3390/computers5020012
Chicago/Turabian StyleMohd Sabri, Norlina, Nor Diyana Md Sin, Mazidah Puteh, and Mohamad Rusop Mahmood. 2016. "Optimization of Nano-Process Deposition Parameters Based on Gravitational Search Algorithm" Computers 5, no. 2: 12. https://doi.org/10.3390/computers5020012
APA StyleMohd Sabri, N., Md Sin, N. D., Puteh, M., & Mahmood, M. R. (2016). Optimization of Nano-Process Deposition Parameters Based on Gravitational Search Algorithm. Computers, 5(2), 12. https://doi.org/10.3390/computers5020012