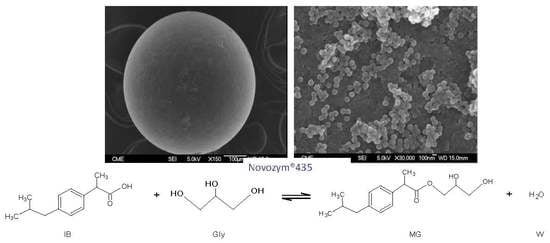
Synthesis of Ibuprofen Monoglyceride in Solventless Medium with Novozym^®435: Kinetic Analysis

Abstract

This study investigates the enzymatic esterification of glycerol and ibuprofen in a solventless medium catalyzed by immobilized lipase B from Candida antarctica (Novozym^®435). Fixing the concentration of this enzymatic solid preparation at 30 g·L⁻¹, and operating at a constant stirring speed of 720 rpm, the temperature was changed between 50 and 80 °C, while the initial concentration of ibuprofen was studied from 20 to 100 g·L⁻¹. Under these conditions, the resistance of external mass transport can be neglected, as confirmed by the Mears criterion (Me < 0.15). However, the mass transfer limitation inside the pores of the support has been evidenced. The values of the effectiveness factor (η) vary between 0.08 and 0.16 for the particle size range considered according to the Weisz–Prater criteria. Preliminary runs permit us to conclude that the enzyme was deactivated at medium to high temperatures and initial concentration values of ibuprofen. Several phenomenological kinetic models were proposed and fitted to all data available, using physical and statistical criteria to select the most adequate model. The best kinetic model was a reversible sigmoidal model with pseudo-first order with respect to dissolved ibuprofen and order 2 with respect to monoester ibuprofen, assuming the total first-order one-step deactivation of the enzyme, with partial first order for ibuprofen and enzyme activity.

1. Introduction

The scarcity and depletion of traditional fossil energy sources and their negative influence on the environment, especially in terms of climate change, are the main reasons behind many efforts in technological and scientific research and development currently. The 2015 United Nations Climate Change Conference in Paris aimed at a full international commitment to avoid an increase in the global average temperature of higher than 2 °C. This political impulse is boosting the production of renewable energies, including biofuels. Glycerol is a plentiful by-product of the biodiesel manufacturing process. Owing to the saturation of the glycerol market, the price of this chemical has dropped in the last years [1,2]. Therefore, new uses of this polyol are being investigated as glycerol is looked upon as the new C3 platform chemical [1,3].

The isoform B of the lipase (EC.3.1.1.3) from Candida antarctica (CALB) has been widely employed for organic synthesis. It has excellent activity and thermal stability, with high stereospecificity [4], and exhibits high enantioselectivity toward secondary [5] and tertiary alcohols [6]. Novozym^®435 is a commercially available heterogeneous biocatalyst Candida antarctica lipase B. This enzyme preparation has been used in the esterification of profens such as naproxen [7], ibuprofen [8,9], flurbiprofen [10], and ketoprofen [11] for the synthesis of prodrugs; it has also been used in the production of biodiesel [12,13,14] and in the development of polymerization bioprocesses [15,16,17]. It can actuate when suspended in various solvents and renewable resources such as supercritical carbon dioxide, ionic liquids [18], glycerol [19,20,21], and deep eutectic solvents (DES), the high viscosity of which, as in the case of glycerol, can be reduced by water addition [22]. In a very recent review, Novozym^®435, as the most successful enzyme preparation, has been discussed both in terms of its success in several applications and its drawbacks, which are mainly related to its mechanical weakness, its support solubility in some organic solvents, and its trend of accumulating hydrophilic compounds in hydrophobic environments, due to a certain amphiphilicity, that results in its deactivation in some applications, as in the production of biodiesel [23].

In recent times, a broad variety of immobilization methods have been applied to lipases. Therefore, different proven immobilization techniques have been developed, including [24] (a) covalent bonds, (b) cross-linking, including CLEAs [22], (c) entrapment in gel matrices, (d) adsorption, and (e) inclusion in membranes. Immobilization can enhance the stability, activity, and selectivity of the enzyme [25]. Enzyme immobilization allows for its easy separation from the reaction medium [26] and facile reuse, or utilization in continuous—or flow—reactors [27,28]. In spite of this, the activity may be reduced by losing access to active centers and by the hindered diffusion of substrates and products [15,28,29]. In particular, a major limitation is the slow mass transport within the porous structure (internal mass transfer) or in the outer liquid layer (external mass transfer), in comparison to the reaction rate [26,30]. The high viscosity of the liquid phase in combination with the high enzyme concentration in the solid can lead to mass transfer hindrances, which can be reduced by a wise selection of agitation speeds or flow rates and enzyme loadings [31]. From a more in-depth perspective, in-situ techniques can render local and particle information on the enzyme distribution, local diffusion, structural features and local mobility of the enzyme, which is critical to the optimization of immobilized biocatalysts in a multiscale approach [32].

Traditionally, enzyme immobilization enhances its stability over a broad pH and temperature range. However, deactivation continues to be a major issue when using lipases as biocatalysts in industrial applications. For these enzymes, there are several reports in the literature focused on their thermal deactivation [33,34] or chemical deactivation due to acids [35,36]. For example, in the hydrolysis of phenyl benzoate using Novozym^®435, the enzyme was inactivated by the combined action of substrate (hydrazine) and product (phenol). Thus, the deactivation kinetic model included two serial first-order reactions [37]. Similarly, in the epoxidation of styrene, Novozym^®435 was deactivated by three parallel contributions, with the deactivation rate described by first-order kinetics with respect to hydrogen peroxide, to perlauric acid, and to the thermal contribution [38].

Profens are over-the-counter drugs that are widely used to reduce pain, inflammation and fever. Their action is due to the inhibition of cyclooxygenase (COX) enzymes, thus reducing the production of prostaglandins. Complications arise due to the inhibition of COX 1, a key enzyme for the protection of the gastrointestinal tract, in particular when the enzyme is dispensed for a long time. Profens prodrugs, including glycerides of profens, permit the slow action of the drug in the body, reducing secondary effects [20,39]. Several works on lipase kinetics regarding profen esterification in organic media are available [7,40]. In fact, several models have been proposed to explain the lipase-catalyzed esterification of profens in organic media, most of them based on the ping-pong bi–bi mechanism. In recent years, solventless catalytic and biocatalytic processes have emerged as an economic and environmentally friendly alternative. In this line, in a previous work [20], the esterification of glycerol and ibuprofen using free enzyme CALB in solventless medium was studied, with the kinetic model proposed being a simple reversible Michaelis–Menten model of pseudo-first order with respect to the concentration of ibuprofen and monoglyceride. Furthermore, Tamayo et al. [19] explained the kinetics of the synthesis of glycerol monobenzoate with C. antarctica lipase B in solventless medium according to a simple Michaelis–Menten model with a partial one-step deactivation for the biocatalyst.

The aim of this work is to study the esterification of glycerol with ibuprofen catalyzed by immobilized Candida antarctica lipase B (Novozym^®435) in a solventless medium, represented in Scheme 1, to select the most suitable kinetic model. With this objective, a preliminary study was undertaken regarding the effects of operational conditions such as temperature, reagents concentration, and immobilized enzyme concentration, and the influence of external and internal mass transfer over the overall rate of reaction. Furthermore, a study of the kinetics and the chemical equilibrium under those conditions was performed. Finally, in order to discriminate the most adequate kinetic model among several proposed models, based on previously observed phenomena, the candidate models were fitted to all experimental data available by gradient non-linear regression coupled to the fourth Runge–Kutta integration of the kinetic equations of each model, then applying several physical and statistical criteria in the discrimination process.

2. Results and Discussion

2.1. Effect of Biocatalyst Loading

The influence of the enzymatic solid concentration on the initial rate of esterification was studied between 10 and 40 g·L⁻¹. During the development of the reverse phase high-performance liquid chromatography (HPLC) method, no glyceride species were found except monosaccharides, regardless of the eluent composition; thus, only one reaction happens, as indicated in Scheme 1. As can be seen in Figure 1a, the initial rate of increase with the amount of solid biocatalyst follows a hyperbolic trend. It was found that the ibuprofen monoglyceride yield increased from 40% to 80% with increasing enzyme concentration, until a saturating value seems to be reached. In fact, in multiphasic systems with substrates in two distinct phases, the saturation of the inner catalytic surface by either of them could explain the observed trend. In addition, internal diffusion limitations could happen when the substrate could not reach the inner parts of the biocatalyst support [41,42]. Taking into account the fact that little improvement was observed at values higher than 30 g·L⁻¹ (which corresponds to about 2.4 g·L⁻¹ pure Candida antarctica lipase B [43]), this value was selected as the enzyme concentration for further runs.

2.2. Effect of Temperature and Initial Concentration of Ibuprofen

In the esterification of ibuprofen with glycerol catalyzed by Novozym^®435, several experiments have been studied, varying the temperature between 50 to 80 °C and the initial concentration of ibuprofen between 20 and 100 g·L⁻¹. In all runs, the enzyme concentration (30 g·L⁻¹) and glycerol volume (20 mL) were kept constant. In Figure 2, at high concentrations (60 and 100 g·L⁻¹) at 80 °C, there was a decrease of the initial esterification rate; therefore, the ibuprofen seems to be acting as a strong deactivating agent at high temperature. This phenomenon was also observed in the literature: Chang et al. [44] investigated the effect of the temperature in the synthesis of triglycerides from glycerol and 4-phenylbutyric acid catalyzed by Novozym^®435 and found that the enzyme was deactivated at high temperature (70–80 °C). Besides, in the study by Martins et al. [35], in the production of butylacetate catalyzed by Novozym^®435, the enzyme deactivation was present at a concentration of 0.6 M acetic acid. It is well known that a high concentration of acid may decrease the micro-environmental pH around the active site of lipase, reducing the enzyme activity. Consequently, the probable enzyme deactivation seems to be owed to the synergy between acid and heat. This effect was already detected in other systems and was more markedly evident in the esterification of glycerin with benzoic acid [19]. For this reason, the possible enzyme deactivation by substrate and temperature was considered for the proposal of kinetic models in the final kinetic study.

2.3. Influence of Mass Transfer

2.3.1. External Mass Transfer

To study substrate mass transfer in the outer film surrounding the particle of the immobilized enzyme, runs were performed at stirring speeds from 120 and 840 rpm at 50 and 80 °C with an initial ibuprofen concentration of 60 g·L⁻¹. Figure 3a presents the initial rate of esterification, increasing as the agitation speed rises. At 50 °C, at a low stirring speed, the contact between the phases is very poor owing to the high viscosity of the reaction medium, but it is enhanced by increasing the agitation speed. A similar behavior can be seen at 80 °C; however, the values of the initial rate of esterification are much higher than at 50 °C, as there is an exponential decrease of glycerol viscosity with the increment of temperature and an increase of the reaction rates (Arrhenius behavior). In addition, ibuprofen melts around 70–75 °C; as a consequence, the mass transfer rate might increase, as whole ibuprofen micro-drops can enter the solid pores, diffusing into it by capillary action. In fact, at 80 °C and at stirring rates beyond 600 rpm, no significant change in the initial rate was observed. Similarly, at 50 °C, this fact was evident above 720 rpm. Using a similar approach, Yadav et al. [37] studied the effect of stirring speeds between 200 and 800 rpm in the synthesis of hydrazide benzoic acid using Novozym^®435. They concluded that external mass transfer limitations are negligible above 600 rpm. These data refer to other reactions, but the reaction rates are of the same order of magnitude.

The final yield of ibuprofen monoglyceride is shown in Figure 3b. It can be observed that a stirring speed equal to or higher than 720 rpm did not improve the yield, at least considering the estimated experimental error. Thus, under these conditions, the chemical reaction is the slowest phenomenon and controls the overall rate of the process. To check whether the effect of external mass transfer could be neglected, the Mears criterion [45] was applied using Equation (1), where r_i,obs is the rate of reaction (mol^.L^−1.s⁻¹), d_P is the diameter of biocatalyst particle (m), n is the reaction order, k_L is the mass transfer coefficient (cm^.s⁻¹), and C_i,0 is the bulk concentration of the substrate (mol^.L⁻¹). The mass transfer coefficient was calculated by using Frössling’s correlation [46], defined by Equation (2), using the adimensional numbers given by Equations (3)–(5), where Re is the Reynold number, Sc is the Schmidt number, Sh is the Sherwood number, U is the linear velocity of the particle (m^.s⁻¹), d_p is the diameter of the particle (m), ρ is the density of solvent (kg·m⁻³), µ is the viscosity of solvent (P), and D_ij is the molecular diffusivity of substrate in the solvent (m^2.s⁻¹).

$$Me=\frac{-r_{obs}·d_p·n}{2·k_L·C_{i,0}}.$$

(1)

$$\mathrm{Sh}=2+0.6·{\mathrm{Re}}^{1/2}·{\mathrm{Sc}}^{1/3}$$

(2)

$$\mathrm{Re}=\frac{\mathrm{U}·\mathsf{\rho }·{\mathrm{d}}_{\mathrm{p}}}{\mathsf{\mu }}$$

(3)

$$\mathrm{Sc}=\frac{\mathsf{\mu }}{\mathsf{\rho }·{\mathrm{D}}_{\mathrm{ij}}}$$

(4)

$$\mathrm{Sh}=\frac{{\mathrm{k}}_{\mathrm{L}}·{\mathrm{d}}_{\mathrm{p}}}{{\mathrm{D}}_{\mathrm{ij}}}$$

(5)

With regards to the molecular diffusivity, this parameter was calculated using the Wilke–Chang correlation [47], which is defined by Equations (6) and (7):

$${\mathrm{D}}_{\mathrm{ij}}= \frac{7.4·{10}^{-8}·{\left(\mathsf{\varphi }·{\mathrm{M}}_{\mathrm{j}}\right)}^{0.5}·\mathrm{T}}{{\mathsf{\mu }}_{\mathrm{m}}·{\mathrm{V}}_{\mathrm{i}}^{0.6}}$$

(6)

$${\mathrm{V}}_{\mathrm{i}}=0.285·{\mathrm{V}}_{\mathrm{ci}}^{1.048}$$

(7)

where φ is the adimensional factor of solvent association (we have considered a value of φ = 1.9, owing to the glycerol having a strong molecular interaction which is very similar to the methanol), T is the absolute temperature (K), M_j is the molecular weight of solvent (kg^.mol⁻¹), µ_m is the viscosity of solvent (cP), and V_i is the molar volume of diffusing species at boiling point under normal conditions (m^3.mol⁻¹) (determined by the Tyn and Calus method [48], Equation (7), with V_ci being the critical molar volume (m^3.mol⁻¹), which in relation to the ibuprofen is 200).

The Mears criterion suggests that the reaction is not controlled by the external mass transfer if C_M < 0.15, with the mass transfer rate being faster than the chemical reaction. Me values at a stirring speed of 720 rpm were 9.35 × 10⁻⁵ (50 °C) and 23.7 × 10⁻⁵ (80 °C). These results were considerably smaller that the critical value of 0.15, indicating that external mass transfer resistance was no longer significant at this stirring speed value at both temperatures. Kinetic runs were performed at an agitation speed of 720 rpm to ensure a fast mass transfer in the outer liquid film.

2.3.2. Internal Mass Transfer

The influence of internal mass transfer resistance from Novozym^®435 was investigated by sieving the immobilized enzyme preparation into different particle size fractions of 0.32–0.5, 0.5–0.7, and 0.7–1 mm, with a mean particle size received from the manufacturer of 0.65 mm. Several esterification runs were performed with those fractions, and the whole preparation was performed at 50 and 70 °C, using an initial ibuprofen concentration of 60 g·L⁻¹. Figure 4 shows the initial reaction rate of such runs; it can be observed that, as the mean particle size (d_p) decreases, an increment in the initial esterification rate happens. As a consequence, the mass transfer inside the biocatalyst pores seems to be very significant. In fact, the effect of particle size has been studied in the synthesis of monobenzoate glycerol using Novozym^®435 in the range of 0.075 and 0.65 mm, concluding that internal diffusion is important for the reaction rate of the esterification of benzoic acid with glycerol [49]. In this way, we have estimated the effectiveness factor (η) for the immobilized enzyme, proposing a system of equations for each fraction by using Equation (8), and this was confirmed with the mean fraction results obtained using Equation (9).

Table 1. Values of the effective diffusion coefficient, effectiveness factor, and Weisz–Prater criterion at 50 and 70 °C.

T (°C)	Dij × 1011 (m2 s−1)	De × 1013 (m2 s−1)	Size Fraction % w/w	Size Particle (mm)	RMG × 104 Novozym®435 (mol L−1 min−1)	η	We-Pt
50	1.69	1.35	13	0.32–0.5	2.05	0.16	3.7
			52	0.5–0.7	1.61	0.12	6.2
			35	0.7–1	1.19	0.09	9.3
			Average	0.3–1	1.65	0.12	7.4
70	5.03	4.03	13	0.32–0.5	7.44	0.11	4.4
			52	0.5–0.7	6.04	0.09	7.9
			35	0.7–1	5.18	0.08	10.6
			Average	0.3–1	6.56	0.09	9.8

shows the values of the effectiveness factor calculated according to the aforementioned procedure. These values varied between 0.08 and 0.16 and are less than unity (η < 1). In addition, the average effectiveness factor, at 50 and 70 °C, is very close to that for the particle size 0.5–0.7, as expected. If temperature is considered, an increase in this variable causes a slight decrease in the effectiveness factor. This fact seems surprising, as it is very usual that the effectiveness factor markedly decreases as temperature rises. In this case, an increment in the temperature can significantly enhance the reaction rate, as expected, but also the rate of mass transfer, as the glycerol viscosity dramatically reduces.

$$\frac{{\mathsf{\eta }}_{\mathrm{i}}}{{\mathsf{\eta }}_{\mathrm{j}}}=\frac{{\mathrm{r}}_{\mathrm{obs},\mathrm{i}}}{{\mathrm{r}}_{\mathrm{obs},\mathrm{j}}}, \mathrm{i} = 1, 2; \mathrm{j} = 2, 3, 1$$

(8)

$$\overline{\mathsf{\eta }}={\displaystyle \sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{i}}·{\mathsf{\eta }}_{\mathrm{i}}$$

(9)

where i, j are the values corresponding to each particle size fractions, η is the effectiveness factor of the mean fraction, and x_i is the mass percentage of each particle size fraction.

Besides, the absence of intra-particle diffusion resistance was checked by calculating the Weisz–Prater criterion (Doran, 1995), using Equation (10), while the effective diffusivity coefficient, D_e, can be given as Equation (11). Table 1 compiles the calculated values of the We–Pr numbers, all of which are higher than 3 and increase significantly with the temperature. In addition, the effective diffusivity coefficient increases markedly with temperature—an aspect explained by the trend of viscosity with temperature. As a consequence, the mass transfer rate increases almost at the same pace as the reaction rate, with the result that the effectiveness factor varies very little with temperature. As a conclusion, the values of We–Pt > 3 and effectiveness factor η < 1 suggest that mass transfer limitations are significant in this case.

$$\mathrm{We}-\mathrm{Pt}=\frac{{\mathrm{r}}_{\mathrm{obs}}·{\mathrm{d}}_{\mathrm{p}}^2}{{\mathrm{D}}_{\mathrm{e}}·{\mathrm{C}}_{\mathrm{i},\mathrm{o}}}$$

(10)

$${\mathrm{D}}_{\mathrm{e}}= \frac{{\mathrm{D}}_{\mathrm{ij}}·{\mathsf{\epsilon }}_{\mathrm{p}}·\mathsf{\sigma }}{\mathsf{\tau }}$$

(11)

where r_obs is the rate reaction (mol^.L^−1.s⁻¹), d_P is the diameter of the biocatalyst particle (m), C_i,0 is the bulk concentration of the substrate (mol^.L⁻¹), D_ij is the molecular diffusivity, estimated from the Wilke–Chang equation (Equation (6)), ε_p is the porosity of the particle, σ is the constriction factor, and τ is the tortuosity of the particle. In the literature, the values of porosity (ε) found for Novozym^®435 were 0.35 [50], 0.5 [51], and 0.5 [4]; in this work, we have considered a value of ε = 0.5. Some authors have estimated that σ and τ for Novozym^®435 are 1 and 6, respectively [51]; however, we considered the tortuosity equal to 12 and a constriction factor of 0.2, taking into account the nature of the support and the large size of the enzyme molecules, which could cause hindered diffusion [52].

2.4. Kinetic Modelling

A total of 15 experiments were conducted at a fixed agitation speed of 720 rpm with the temperature ranging between 50 and 80 °C and initial concentrations of ibuprofen of 20 and 100 g·L⁻¹.

Figure 5 shows the conversions at equilibrium achieved within the range of temperatures and initial concentrations of ibuprofen tested. Even considering the experimental error, at 50 to 70 °C, total conversion was not reached in the esterification of ibuprofen with glycerol: the conversion values achieved varied from 95% to 98%, for all concentrations. However, it can be observed for runs at 100 g·L⁻¹ initial concentration of ibuprofen at 75 °C, and at 60 and 100 g·L⁻¹ ibuprofen and 80 °C, that the values of total conversion reached varied from 20% to 30%, suggesting enzymatic deactivation. In this way, the results suggest the reversibility of the reaction on one hand and enzyme deactivation on the other; thus, both phenomena need to be included in any kinetic model considered.

In this manner, the proposed kinetic models of the esterification of glycerol with ibuprofen catalyzed by Novozym^®435 are based on a ping-pong bi–bi mechanism, which has been broadly used to explain esterification and transesterification reactions [53]. The general schematic diagram of the ping-pong bi–bi mechanism can be applied in the present case by the following steps:

$$\mathrm{E}+\mathrm{I}\leftrightarrow \mathrm{EI} \therefore { \mathrm{k}}_1,{\mathrm{k}}_2$$

$$\mathrm{EI} \leftrightarrow {\mathrm{E}}^{\ast }\mathrm{W} \therefore { \mathrm{k}}_{3 },{ \mathrm{k}}_4$$

$${\mathrm{E}}^{\ast }\mathrm{W} \leftrightarrow {\mathrm{E}}^{\ast }+\mathrm{W} \therefore { \mathrm{k}}_5,{ \mathrm{k}}_6$$

$${\mathrm{E}}^{\ast }+\mathrm{Gly} \leftrightarrow {\mathrm{E}}^{\ast }\mathrm{Gly} \therefore { \mathrm{k}}_{7 },{ \mathrm{k}}_8$$

$${\mathrm{E}}^{\ast }\mathrm{Gly} \leftrightarrow \mathrm{EMG} \therefore { \mathrm{k}}_{9 },{ \mathrm{k}}_{10}$$

$$\mathrm{EMG} \leftrightarrow \mathrm{E}+\mathrm{MG} \therefore { \mathrm{k}}_{11 },{ \mathrm{k}}_{12}$$

where E, E*, I, Gly, MG, W, and k_i are the enzyme, intermediate enzyme, ibuprofen, glycerol, ibuprofen monoglyceride, water and the kinetic constant for reaction i, respectively. By taking into account the steps involved in the above reaction scheme, a general kinetic equation for the esterification reaction is as follows [53]:

$$\mathrm{r}=\frac{{\mathrm{k}}_{\mathrm{a}}·{\mathrm{C}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{Gly}}-{\mathrm{k}}_{\mathrm{b}}·{\mathrm{C}}_{\mathrm{MG}}·{\mathrm{C}}_{\mathrm{W}}}{\mathrm{a}·{\mathrm{C}}_{\mathrm{I}}+\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}+\mathrm{c}·{\mathrm{C}}_{\mathrm{MG}}+\mathrm{d}·{\mathrm{C}}_{\mathrm{W}}+\mathrm{e}·{\mathrm{C}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{Gly}}+\mathrm{f}·{\mathrm{C}}_{\mathrm{MG}}·{\mathrm{C}}_{\mathrm{W}}+\mathrm{g}·{\mathrm{C}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{MG}}+\mathrm{h}·{\mathrm{C}}_{\mathrm{Gly}}·{\mathrm{C}}_{\mathrm{W}}}$$

(12)

where

$${\mathrm{k}}_{\mathrm{a}}={\mathrm{k}}_1·{\mathrm{k}}_3·{\mathrm{k}}_5·{\mathrm{k}}_7·{\mathrm{k}}_9·{\mathrm{k}}_{11}·{\mathrm{C}}_{\mathrm{E}}$$

$${\mathrm{k}}_{\mathrm{b}}={\mathrm{k}}_2·{\mathrm{k}}_4·{\mathrm{k}}_6·{\mathrm{k}}_8·{\mathrm{k}}_{10}·{\mathrm{k}}_{12}·{\mathrm{C}}_{\mathrm{E}}$$

$$\mathrm{a}={\mathrm{k}}_1·{\mathrm{k}}_3·{\mathrm{k}}_5·{\mathrm{k}}_8·{\mathrm{k}}_{11}$$

$$\mathrm{b}={\mathrm{k}}_2·{\mathrm{k}}_5·{\mathrm{k}}_7·{\mathrm{k}}_9·{\mathrm{k}}_{11}$$

$$\mathrm{c}={\mathrm{k}}_2·{\mathrm{k}}_4·{\mathrm{k}}_6·{\mathrm{k}}_8·{\mathrm{k}}_{11}$$

$$\mathrm{d}={\mathrm{k}}_2·{\mathrm{k}}_5·{\mathrm{k}}_8·{\mathrm{k}}_{10}·{\mathrm{k}}_{12}$$

$$\mathrm{e}={\mathrm{k}}_1·{\mathrm{k}}_5·{\mathrm{k}}_7·{\mathrm{k}}_{11}·({\mathrm{k}}_3+{\mathrm{k}}_9)$$

$$\mathrm{f}={\mathrm{k}}_2·{\mathrm{k}}_5·{\mathrm{k}}_8·{\mathrm{k}}_{12}·({\mathrm{k}}_4+{\mathrm{k}}_{10})$$

$$\mathrm{g}={\mathrm{k}}_1·{\mathrm{k}}_6·{\mathrm{k}}_8·{\mathrm{k}}_{11}·({\mathrm{k}}_3+{\mathrm{k}}_4)$$

$$\mathrm{h}={\mathrm{k}}_2·{\mathrm{k}}_5·{\mathrm{k}}_7·{\mathrm{k}}_{12}·({\mathrm{k}}_9+{\mathrm{k}}_{10})$$

In our case, the glycerol is present in a very large excess (C_Gly is constant). Also, we have considered that the product concentrations are identical (C_W = C_MG). In this way, by rearranging Equation (12) and assuming that ${\mathrm{K}}_{\mathrm{A}}·{\mathrm{C}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{Gly}} \approx 0$ and ${\mathrm{K}}_{\mathrm{B}}·{\mathrm{C}}_{\mathrm{MG}}^2\approx 0,$ we obtain Equation (13):

$$\mathrm{r}=\frac{{\mathrm{k}}_1^{\ast }·{\mathrm{C}}_{\mathrm{I}}-{\mathrm{k}}_2^{\ast }·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{I}}+{\mathrm{K}}_{\mathrm{MG}}·{\mathrm{C}}_{\mathrm{MG}}}$$

(13)

where

$${\mathrm{k}}_1^{\ast }=\frac{{\mathrm{k}}_{\mathrm{a}}}{\mathrm{b}}$$

$${\mathrm{k}}_2^{\ast }=\frac{{\mathrm{k}}_{\mathrm{b}}}{\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}}$$

$${\mathrm{K}}_{\mathrm{I}}=\frac{\mathrm{a}}{\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}}-\frac{\mathrm{e}}{\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}}$$

$${\mathrm{K}}_{\mathrm{MG}}=\frac{\mathrm{c}+\mathrm{d}}{\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}}-\frac{\mathrm{h}}{\mathrm{b}}$$

$${\mathrm{K}}_{\mathrm{A}}=\frac{\mathrm{g}}{\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}}$$

$${\mathrm{K}}_{\mathrm{B}}=\frac{\mathrm{f}}{\mathrm{b}·{\mathrm{C}}_{\mathrm{Gly}}}$$

In a previous work, Ravelo et al. [20] demonstrated that the liquid enzymatic preparation CALB-L was not deactivated by the effect of temperature and initial concentration of ibuprofen. However, according to the preliminary experiments, using the immobilized form of the CALB (Novozym^®435), there is a strong enzymatic deactivation due to the synergy between acid concentration and temperature. For this reason, we have proposed a kinetic model involving irreversible deactivation that obeys both Equations (13) and (14), with the reaction rate being of partial order 1 with respect to the concentration of ibuprofen and to the remaining activity.

$$-\frac{{\mathrm{da}}_{\mathrm{R}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{d}}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{I}}$$

(14)

where k_d is the deactivation constant, a_R is the remaining activity, and C_I is the ibuprofen concentration.

Equations (13) and (14) were fitted to kinetic data by applying a nonlinear fitting coupled to the numerical integration of such equations using the software Aspen Custom Modeler. The estimation of the adsorption constant (K_I and K_MG) rendered the following values, with their error intervals, of K_I = 35.5 ± 7.78 and K_MG = 5 ± 3.44.

Therefore, the immobilized enzyme CALB (c) has more affinity for ibuprofen than for its monoglyceride, as the adsorption constant K_I is seven-fold larger than K_MG. In consequence, the monoglyceride effect in the denominator could be looked upon as negligible, and the first proposed kinetic model is a reversible hyperbolic model pseudo-first order model with respect to the concentration of ibuprofen and second order with respect to concentration of monoglyceride, adding the enzymatic deactivation effect. Thus, Model 1 is defined by Equations (14) and (15):

$$\mathrm{r}=\frac{{\mathrm{k}}_1^{\ast }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{I}}-{\mathrm{k}}_2^{\ast }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{I}}}$$

(15)

Similarly, Model 2 considers the deactivation of the enzyme (Equation (14)), and the main rate equation defined by Equation (16). Furthermore, this model assumes the possibility that the solubility of ibuprofen in the reaction medium increases with the reaction time and temperature, which is established by defining an effective concentration of reactive ibuprofen (C_IR0) and also including the concentration of ibuprofen monoglyceride (C_MG), due to its capacity to enhance the scarce mutual solubility of ibuprofen and glycerol; the ibuprofen solubility is defined by Equation (17). This fact was demonstrated in a prior study [20]. Hence, Model 3 is expressed by

$$\mathrm{r}=\frac{{\mathrm{k}}_1^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{IR}}-{\mathrm{k}}_2^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{IR}}}$$

(16)

$${\mathrm{S}}_{\mathrm{IR}}={\mathrm{C}}_{\mathrm{IR}0}+{\mathrm{k}}_{\mathrm{s}}·{\mathrm{C}}_{\mathrm{MG}}$$

(17)

C_I ≥ S_IR ⇒ C_IR=S_IR

C_I < S_IR ⇒ C_IR=C_I

where k_s is the constant used to describe the solubility of ibuprofen in the reaction medium, S_IR is the ibuprofen solubility, and C_IR represents the reactive ibuprofen concentration. In addition, in both models (1 and 2), the effectiveness factor considered was 0.11, which corresponds to that calculated for the mean fraction size.

The kinetic parameters of the aforementioned models were calculated by nonlinear regression algorithms coupled to the numerical integration of such models during fitting to experimental data. After obtaining the value of the kinetic constant (or constants) at each temperature, estimates of E_a/R were retrieved, from which the simultaneous fitting of each kinetic model to all data at all temperatures was performed to obtain the multivariable fitting parameters.

Table 2. Kinetic models with their kinetic constants, with the standard error for each constant, tested by fitting the retrieved data of the enzymatic esterification of ibuprofen and glycerol. In bold, the kinetic parameters, together with their values and errors, which correspond to the selected kinetic model.

Model	Rate Equations	Parameters	Value	Error
1	$$\begin{gathered} \mathrm{r}=\frac{{\mathrm{k}}_1^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{I}}-{\mathrm{k}}_2^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{I}}} \\ -\frac{{\mathrm{da}}_{\mathrm{R}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{d}}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{I}} \end{gathered}$$	lnk′10	13.14	0.32
		Eak′1/R	6999	107
		lnk′20	22.57	3.88
		Eak′2/R	10,679	1311
		lnkd0	85.43	1.86
		Eakd/R	33,111	654
		KI	17.97	1.02
2	$$\begin{gathered} \mathrm{r}=\frac{{\mathrm{k}}_1^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{IR}}-{\mathrm{k}}_2^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{IR}}} \\ {\mathrm{S}}_{\mathrm{IR}}={\mathrm{C}}_{\mathrm{IR}0}+{\mathrm{k}}_{\mathrm{s}}·{\mathrm{C}}_{\mathrm{MG}} \end{gathered}$$ Si CI ≥ SIR ⇒ CIR=SIR Si CI < SIR ⇒ CIR=CI $-\frac{{\mathrm{da}}_{\mathrm{R}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{d}}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{I}}$	lnk′10	15.45	0.44
		Eak′1/R	7800	148
		lnk′20	19.58	2.35
		Eak′2/R	9562	794
		lnks0	−31.3	2.45
		Eaks/R	−10,610	812
		lnkd0	89.13	1.97
		Eakd/R	32408	690
		KI	11.14	0.58

compiles those kinetic parameters with their standard errors for the two proposed kinetic models, while

Table 3. Goodness-of-fit and over-parameterization statistical parameters of the tested kinetic models for the enzymatic esterification of ibuprofen and glycerol. SQR: sum of quadratic residues; AICc: Akaike information criterion; BIC: Bayesian information criterion; RMSE: root mean square error. In bold, the statistical parameters corresponding to the selected kinetic model.

Model	F-Value	SQR	AICc	BIC	RMSE	VE (%)
1	10863	1.18	−3833	−3847	0.06	98.43
2	13995	0.88	−4010	−4028	0.04	98.82

shows the statistical parameters describing the goodness-of-fit of such models. In this way, the first physical criterion applied to reject models is a positive sign in all adsorption or equilibrium constants, which is met by all models tested. A second physical criterion is the inclusion of activation energies of the kinetic constant, as displayed in Table 2, in a reasonable interval of values; considering Models 1 and 2 for the direct reaction, its kinetic constant has activation energies of 58.2 and 64.8 kJ mol⁻¹, respectively. With regard to the values of the kinetic constants for the reverse reaction of Models 1 and 2, they have activation energies of 88.8 and 79.5 kJ·mol⁻¹, respectively. It is well known that the activation energies in the chemical reaction step usually acquire values in the interval of 2 to 200 kJ mol⁻¹. Another physical criterion that is applicable in this case is the shape of the curves of conversion to the monoglyceride with reaction time: if they are sigmoidal, as shown in Figure 6 for low temperatures, it can be deduced that a progressive acceleration of the overall rate of the process happens—a phenomenon that can be explained by a progressive solubilization of one of the reagents, with a concomitant increase of its concentration in the reacting liquid due to this effect. This trend is only contemplated in Model 2.

The first statistical criterion is a low value for the absolute value of the standard error of a given kinetic constant compared to the absolute value of this constant. As can be seen in Table 2, the constants and parameters for all models show very low standard errors; or, in other words, very low minimum t-values or narrow intervals of error at 95% confidence. Considering the p-values for all models (<0.0001), they are sound enough to be tested (a conclusion that could be reached considering the results from the preliminary experiments). Therefore, to select the best model in statistical terms, it is necessary to apply information and goodness-of-fit criteria such as the F-value, root mean square error (RMSE), Bayesian information criterion (BIC), and Akaike information criterion (AICc). Of these statistical parameters, the values of root mean square error (RMSE), AICc, and BIC are the lowest for Model 2, while the F-value is the highest for the same Model 2. According to this, Model 2 has an excellent goodness-of-fit and narrow interval for kinetic constants and is thus statistically sound.

As mentioned previously [20], the esterification of glycerol and ibuprofen drives the free enzyme preparation (Lipozyme CALB L), which proceeds in a biphasic solid–liquid system at temperatures lower than 70 °C and in a biphasic liquid–liquid system at temperatures higher than that value; even at 80 °C, there is no apparent deactivation, and a ibuprofen conversion higher than 90% is achieved in 5 h. This stability can be explained in terms of the preferential hydration of the enzyme and minimal molecular contact with glycerol, thus increasing the enzyme rigidity and its stability [54]. The stabilizing effect of glycerol is even more evident in the formulation and use of deep eutectic solvents (DEPs) based on this polyol for lipase-driven reactions [55]. As regards the effect of the solid support of Novozym^®435 on the stability of the lipase, Lewatit^®VP OC 1600 resin seems to be amphiphilic, so it adsorbs (and absorbs) hydrophobic components in hydrophilic environments and, on the contrary, hydrophilic compounds—such as glycerol—in hydrophobic environments such as oils in the biodiesel process [23]. Its aromatic nature can explain a preference for the adsorption of phenolics, as it is a polymethayacryldivinylbenzene copolymer, and it is indeed used as an adsorbing agent, according to Lanxess, the manufacturing company. Thus, apart from the deactivating nature of ibuprofen as a phenolic acid, it can be hypothesized that ibuprofen trends to accumulate in the vicinity of the immobilized enzyme, driving the stabilizing glycerol out of the partition layer, and decreasing, in this manner, the stability of CALB.

Hence, the application of all physical and statistical criteria suggests a reversible sigmoidal model with pseudo-first order with respect to ibuprofen and order 2 with respect to monoester ibuprofen, adding a total deactivation of the enzyme, with a partial first-order for ibuprofen and the enzyme remaining activity. The model is given the following equations:

$$\begin{gathered} \mathrm{r}=\frac{{\mathrm{k}}_1^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{IR}}-{\mathrm{k}}_2^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{IR}}} \\ {\mathrm{k}}_1^{\prime }=\exp \left[15.14\pm 0.44 -\frac{7800 \pm 148}{\mathrm{T}}\right] \\ {\mathrm{k}}_2^{\prime }=\exp \left[19.58\pm 2.35-\frac{9562 \pm 794}{\mathrm{T}}\right] \\ {\mathrm{K}}_{\mathrm{I}}=11.14\pm 0.58 \\ {\mathrm{S}}_{\mathrm{IR}}={\mathrm{C}}_{\mathrm{IR}0}+{\mathrm{k}}_{\mathrm{s}}·{\mathrm{C}}_{\mathrm{MG}};{ \mathrm{k}}_{\mathrm{s}}^{\prime }=\exp -\left[31.3\pm 2.45+\frac{10610 \pm 812}{\mathrm{T}}\right] \\ -\frac{{\mathrm{da}}_{\mathrm{R}}}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{d}}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{I}} ; {\mathrm{k}}_{\mathrm{d}}^{\prime }=\exp \left[89.13\pm 1.97- \frac{32408 \pm 690}{\mathrm{T}}\right] \end{gathered}$$

The fitting of Model 2 to all collected experimental data at 50 and 80 °C and initial concentrations of ibuprofen 20 to 100 g·L⁻¹ is displayed in Figure 6. The goodness-of-fit of the mentioned model and its ability to represent the temporal evolution of the reacting system in the experimental conditions interval studied are evident, given the low absolute errors or deviations observed between experimental data (scattered points) and estimated data with the selected model (lines).

3. Materials and Methods

3.1. Materials

Novozym^®435 (immobilized lipase B from Candida antarctica on macroporous polyacrylate Lewatit VPOC 1600) was kindly gifted by Novozymes A/S (Denmark). Ibuprofen sodium salt (α-methyl-4-(isobutyl) phenylacetic acid) was provided by Sigma-Aldrich. Ibuprofen was prepared by acid precipitation, filtration and drying, as stated in previous works [20]. Other reagents employed in the present research were extra pure glycerol 99.98% UPS grade, methanol HPLC grade (Fisher Scientific UK Ltd., Loughborough, UK), hydrochloric acid (35% w/w, Panreac Quimica S.L.U., Castellar del Valles, Barcelona, Spain), and dimethylsulfoxide-d6 99.8% (Scharlab S.L., Sentmenat, Barcelona, Spain).

3.2. Methods

3.2.1. Enzymatic Esterification of Ibuprofen Ester

In every run, a fixed amount of ibuprofen (0.5 to 2.5 g) was dispersed in 20 mL glycerol, forming a solid–liquid phase at temperatures lower than 70 °C, and a liquid–liquid system at higher temperatures. Runs were performed in a reactor inside a glycerin bath (IKA Yellow Line, model MSC basic C), with controlled temperature and agitation, and started by adding a certain amount of the biocatalyst (time = 0). No pH control was employed in this case, as ibuprofen is a very weak acid (pK_a = 4.85 for the strongest acid species). Samples of 250 µL were taken at particular time values and immediately frozen to quench the reaction. After defrosting, these samples were diluted with 750 µL of pure methanol and centrifuged. Further dilution was performed by taking 100 µL of the diluted sample and mixing it with another 900 µL of pure methanol. The final diluted samples were analyzed by reverse-phase HPLC.

3.2.2. Analytical Methods

The concentrations of analytes of interest in the diluted samples were measured by reverse phase chromatography, with a JASCO HPLC system. The column was a Mediterranean Sea-18 column (Teknokroma Analitica S.A., Sant Cugat del Valles, Barcelona, Spain), while the operational conditions were 35 °C in the column oven and a water–methanol solution as eluent (H₂SO₄ 5 mM (pH 2.2), 83% of methanol) flowing at 0.8 mL·min⁻¹. A diode array detector (DAD) was employed in order to measure ibuprofen and its monoglyceride concentrations at 220 nm, for which the sum of areas for each sample was of use in the correction of the concentrations of both acid and ester [20], which are key to calculating the production rate of the ester with the following equation:

$${\mathrm{R}}_{\mathrm{MG}}=\frac{{\mathrm{k}}_1^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{IR}}-{\mathrm{k}}_2^{\prime }·{\mathrm{C}}_{\mathrm{E}0}·{\mathrm{a}}_{\mathrm{R}}·{\mathrm{C}}_{\mathrm{MG}}^2}{1+{\mathrm{K}}_{\mathrm{I}}·{\mathrm{C}}_{\mathrm{IR}}}$$

(18)

3.2.3. Statistical Methods

Aspen Custom Modeler v10.0 was the software utilized to fit the proposed kinetic model to the available experimental data. To this end, a combination of numerical integration of the differential equations of the models (a fourth-order Runge-Kutta algorithm) coupled and non-linear regression fitting by using the Marquardt–Levenberg method was needed. The proposed kinetic models were fitted step-by-step to data at a fixed temperature in the first place, with the purpose of obtaining an initial guess of the activation energy and neperian logarithm of the pre-exponential factor from the values of the kinetic constants retrieved thereof. These values were the starting values for the final fitting of the proposed kinetic models to the entire set of experimental data (data retrieved at all temperatures and initial concentrations of substrate).

The selection of the most appropriate kinetic model was performed following physical and statistical criteria. The considered physical criteria applied were the sign of adsorption or equilibrium constants, adequate values for the activation energies of the kinetic constants, and the shape of the kinetic curves at each temperature. Statistical criteria involved several goodness-of-fit parameters and the confidence intervals of the kinetic parameters at 95% confidence. The goodness-of-fit statistical parameters here employed take into account the amount of data, the number of kinetic parameters, and the total sum of residuals, giving a precise account of goodness-of-fit of the estimated monoglyceride yield values to the experimental ones and over-parameterization. As indicated in a previous work [23], these parameters were the sum of squared residuals (SSR), the square root of the mean square error (RMSE) (Equation (19)), Fischer’s F-value, as defined in Equation (20), the Akaike information criteria corrected for a low ratio of data number to parameter number (N/K < 40) or AICc (Equation (21)), and the Bayesian information criterion (BIC) (Equation (22)).

$$\mathrm{RMSE}=\sqrt{{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{t}}}\frac{\mathrm{SSR}}{{\mathrm{N}}_{\mathrm{t}}}}=\sqrt{{\displaystyle \sum }_{\mathrm{i}=1}^{{\mathrm{N}}_{\mathrm{t}}}\frac{{\left({\mathrm{y}}_{\mathrm{e}}-{\mathrm{y}}_{\mathrm{c}}\right)}_{\mathrm{i}}^2}{{\mathrm{N}}_{\mathrm{t}}}}$$

(19)

$$\mathrm{F}-\mathrm{value}=\frac{{{\displaystyle \sum }}_{\mathrm{n}-1}^{{\mathrm{N}}_{\mathrm{t}}}\frac{{\left({\mathrm{y}}_{\mathrm{c}}\right)}^2}{\mathrm{K}}}{{{\displaystyle \sum }}_{\mathrm{n}-1}^{{\mathrm{N}}_{\mathrm{t}}}\frac{{\left({\mathrm{y}}_{\mathrm{e}}-{\mathrm{y}}_{\mathrm{c}}\right)}^2}{{\mathrm{N}}_{\mathrm{t}}-\mathrm{K}}}$$

(20)

$$\mathrm{AICc}={\mathrm{N}}_{\mathrm{t}}·\mathrm{Ln}\left(\frac{\mathrm{SSR}}{{\mathrm{N}}_{\mathrm{t}}}\right)+2·\mathrm{K}+\frac{2·\mathrm{K}·\left(\mathrm{K}+1\right)}{{\mathrm{N}}_{\mathrm{t}}-\mathrm{K}-1}$$

(21)

$$\mathrm{BIC}=\mathrm{Ln}\left(\frac{\mathrm{SSR}}{{\mathrm{N}}_{\mathrm{t}}}\right)+\frac{\mathrm{K}}{{\mathrm{N}}_{\mathrm{t}}}\mathrm{Ln}\left({\mathrm{N}}_{\mathrm{t}}\right)$$

(22)

4. Conclusions

In the enzymatic esterification of ibuprofen and glycerol using immobilized Novozym^®435 as a catalyst in solventless conditions, the activity was observed to increase until it reached asymptotic values with increasing enzyme concentration, stirring speed, and initial concentration of ibuprofen. The most adequate operational conditions were an enzyme concentration of 30 g·L⁻¹, a stirring speed of 720 rpm, a temperature from 50 to 80 °C, and an initial concentration of ibuprofen from 20 to 100 g·L⁻¹.

The effect of the external mass transfer was determined in the esterification of glycerol with ibuprofen catalyzed by immobilized Novozym^®435 in solventless medium. For a stirring speed of 600–840 rpm, there are no significant changes in the initial rate of esterification. Under these conditions, the resistance of the external mass transport can be neglected, as confirmed by the Mears criterion (Me < 0.15). In the study of mass transfer limitation in the pores of the support, the existence of significant resistance transport inside the solid particle was evidenced. The effectiveness factor η was determined, with values varying from 0.08 to 0.16 for decreasing particle sizes as obtained from the original biocatalyst by sieving. The Weisz–Prater criterion confirmed the relevance of mass transfer as a limiting phenomenon, reducing the overall, or observed, production rate.

Ibuprofen acts as a deactivating agent, with the deactivation being more evident when the temperature is increased. Therefore, the enzyme deactivation is due to a synergic action of ibuprofen (acid) and temperature. The selected kinetic model is a reversible sigmoidal model of pseudo-first order with respect to ibuprofen and order 2 with respect to monoester ibuprofen, adding a total deactivation of the enzyme with a partial first-order for ibuprofen and for the enzyme’s remaining activity. This model takes into account a limiting and progressive solubilization of solid ibuprofen at 50 and 60 °C.