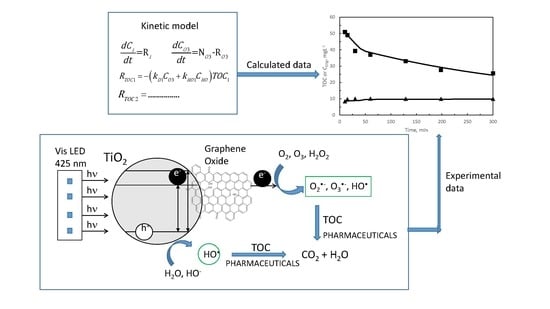
Modeling the Mineralization Kinetics of Visible Led Graphene Oxide/Titania Photocatalytic Ozonation of an Urban Wastewater Containing Pharmaceutical Compounds
Abstract
:1. Introduction
2. Results and Discussion
2.1. First Reaction Period
2.1.1. Kinetic Modeling of Pharmaceuticals Oxidation in a SEMWW Due to Direct Ozone Reactions
2.2. Second Reaction Period
2.2.1. Kinetic Modeling of TOC Removal during the Second Reaction Period with Slow Gas–Liquid Reactions
● Mean Rate of Photon Absorption
● Solution of the Kinetic Model
2.3. Analysis of Variance
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ternes, T.A.; Joss, A.; Siegrist, H. Scrutinizing pharmaceuticals and personal care products in wastewater treatment. Environ. Sci. Technol. 2004, 38, 392A–399A. [Google Scholar] [CrossRef] [Green Version]
- Tran, N.H.; Reinhard, M.; Gin, K.Y.-H. Occurrence and fate of emerging contaminants in municipal wastewater treatment plants from different geographical regions—A review. Water Res. 2018, 133, 182–207. [Google Scholar] [CrossRef]
- Lapworth, D.J.; Baran, N.; Stuart, M.E.; Ward, R.S. Emerging organic contaminants in groundwater: A review of sources, fate and occurrence. Environ. Pollut. 2012, 163, 287–303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- González, S.; López-Roldán, R.; Cortina, J.L. Presence and biological effects of emerging contaminants in Llobregat River basin: A review. Environ. Pollut. 2012, 161, 83–92. [Google Scholar] [CrossRef] [PubMed]
- Pal, A.; Gin, K.Y.H.; Lin, A.Y.C.; Reinhard, M. Impacts of emerging organic contaminants on freshwater resources: Review of recent occurrences, sources, fate and effects. Sci. Total Environ. 2010, 408, 6062–6069. [Google Scholar] [CrossRef] [PubMed]
- López-Pacheco, I.Y.; Silva-Núñez, A.; Salinas-Salazar, C.; Arévalo-Gallegos, A.; Lizarazo-Holguin, L.A.; Barceló, D.; Iqbal, M.N.; Parra-Saldívar, R. Anthropogenic contaminants of high concern: Existence in water resources and their adverse effects. Sci. Total Environ. 2019, 690, 1068–1088. [Google Scholar] [CrossRef]
- Wang, J.; Shih, Y.; Wang, P.Y.; Yu, Y.; Su, J.F.; Huang, C. Hazardous waste treatment technologies. Water Environ. Res. 2019, 91, 1177–1198. [Google Scholar] [CrossRef]
- Kanakaraju, D.; Glass, B.D.; Oelgemöller, M. Advanced oxidation process-mediated removal of pharmaceuticals from water: A review. J. Environ. Manag. 2018, 219, 189–207. [Google Scholar] [CrossRef]
- Salimi, M.; Esrafili, A.; Gholami, M.; Jafari, A.J.; Kalantary, R.R.; Farzadkia, M.; Kermani, M.; Sobhi, H.R. Contaminants of emerging concern: A review of new approach in AOP technologies. Environ. Monit. Assess. 2017, 189, 414. [Google Scholar] [CrossRef]
- Gogate, P.R.; Pandit, A.B. A review of imperative technologies for wastewater treatment II: Hybrid methods. Adv. Environ. Res. 2004, 8, 553–597. [Google Scholar] [CrossRef]
- Gomes, J.; Costa, R.; Quinta-Ferreira, R.M.; Martin, R.C. Review Application of ozonation for pharmaceuticals and personal care products removal from water. Sci. Total Environ. 2017, 586, 265–283. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Chen, H. Catalytic ozonation for water and wastewater treatment: Recent advances and perspective. Sci. Total Environ. 2020, 704, 135249. [Google Scholar] [CrossRef] [PubMed]
- Katsoyiannis, I.A.; Canonica, S.; von Gunten, U. Efficiency and energy requirements for the transformation of organic micropollutants by ozone, O3/H2O2 and UV/H2O2. Water Res. 2011, 45, 3811–3822. [Google Scholar] [CrossRef] [PubMed]
- Glaze, W.H.; Kang, J.W.; Chapin, D.H. The chemistry of water treatment processes involving ozone, hydrogen peroxide and ultraviolet radiation. Ozone Sci. Eng. 1987, 9, 335–342. [Google Scholar] [CrossRef]
- Agustina, T.E.; Ang, H.M.; Vareek, V.K. A review of synergistic effect of photocatalysis and ozonation on wastewater treatment. J. Photochem. Photobiol. C 2005, 6, 264–273. [Google Scholar] [CrossRef]
- Mehrjouei, M.; Müller, S.; Möller, D. A review on photocatalytic ozonation used for the treatment of water and wastewater. Chem. Eng. J. 2015, 263, 209–219. [Google Scholar] [CrossRef]
- Mecha, A.C.; Onyango, M.S.; Ochieng, A.; Momba, M.N.B. Ultraviolet and solar photocatalytic ozonation of municipal wastewater: Catalyst reuse, energy requirements and toxicity assessment. Chemosphere 2017, 186, 669–676. [Google Scholar] [CrossRef]
- Rodríguez, E.M.; Rey, A.; Mena, E.; Beltrán, F.J. Application of solar photocatalytic ozonation in water treatment using supported TiO2. Appl. Catal. B Environ. 2019, 254, 237–245. [Google Scholar] [CrossRef]
- Fernandes, E.; Martins, R.C.; Gomes, J. Photocatalytic ozonation of parabens mixture using 10% N-TiO2 and the effect of water matrix. Sci. Total Environ. 2020, 718, 137321. [Google Scholar] [CrossRef]
- Rey, A.; García-Muñoz, P.; Hernández-Alonso, M.D.; Mena, E.; García-Rodríguez, S.; Beltrán, F.J. WO3-TiO2 based catalysts for the simulated solar radiation assisted photocatalytic ozonation of emerging contaminants in a municipal wastewater treatment plant effluent. Appl. Catal. B Environ. 2014, 154–155, 274–284. [Google Scholar] [CrossRef]
- Yang, T.; Peng, J.; Zheng, Y.; He, X.; Hou, Y.; Wu, L.; Fu, X. Enhanced photocatalytic ozonation degradation of organic pollutants by ZnO modified TiO2 nanocomposites. Appl. Catal. B Environ. 2018, 221, 223–234. [Google Scholar] [CrossRef]
- Dreyer, D.R.; Park, S.; Bielawski, C.W.; Ruoff, R.S. The chemistry of graphene oxide. Chem. Soc. Rev. 2010, 39, 228–240. [Google Scholar] [CrossRef] [PubMed]
- Beltrán, F.J.; Álvarez, P.M.; Gimeno, O. Graphene-Based Catalysts for Ozone Processes to Decontaminate Water. Molecules 2019, 24, 3438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Checa, M.; Figueredo, M.; Aguinaco, A.; Beltrán, F.J. Graphene oxide/titania photocatalytic ozonation of primidone in a visible LED photoreactor. J. Hazard. Mater. 2019, 369, 70–78. [Google Scholar] [CrossRef]
- Matafonova, G.; Batoev, V. Recent advances in application of UV light-emitting diodes for degrading organic pollutants in water through advanced oxidation processes: A review. Water Res. 2018, 132, 177–189. [Google Scholar] [CrossRef]
- Liao, G.; Zhu, D.; Zheng, J.; Yin, J.; Lan, B.; Li, L. Efficient mineralization of bisphenol A by photocatalytic ozonation with TiO2–graphene hybrid. J. Taiwan Inst. Chem. Eng. 2016, 67, 300–305. [Google Scholar] [CrossRef]
- Sheydaei, M.; Shiadeh, H.R.K.; Ayoubi-Feiz, B.; Ezzati, R. Preparation of nano N-TiO2/graphene oxide/titan grid sheets for visible light assisted photocatalytic ozonation of cefixime. Chem. Eng. J. 2018, 353, 138–146. [Google Scholar] [CrossRef]
- Pedrosa, M.; Pastrana-Martínez, L.M.; Pereira, F.R.; Faria, J.L.; Figueiredo, J.L.; Silva, A.M.T. N/S-doped graphene derivatives and TiO2 for catalytic ozonation and photocatalysis of water pollutants. Chem. Eng. J. 2018, 348, 888–897. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Checa, M. Comparison of graphene oxide titania catalysts for their use in photocatalytic ozonation of water contaminants: Application to oxalic acid removal. Chem. Eng. J. 2020, 385, 123922. [Google Scholar] [CrossRef]
- Checa, M.; Beltrán, F.J.; Rivas, F.J.; Cordero, E. On the role of a graphene oxide/titania catalyst, visible LED and ozone in removing mixtures of pharmaceutical contaminants from water and wastewater. Environ. Sci. Water Res. Technol. 2020, 6, 2352–2364. [Google Scholar] [CrossRef]
- Cernigoj, U.; Stangar, U.L.; Trebse, P. Degradation of neonicotinoid insecticides by different advanced oxidation processes and studying the effect of ozone on TiO2 photocatalysis. Appl. Catal. B Environ. 2007, 75, 229–238. [Google Scholar] [CrossRef]
- Rey, A.; Quinones, D.H.; Alvarez, P.M.; Beltran, F.J.; Plucinski, P.K. Simulated solarlight assisted photocatalytic ozonation of metoprolol over titania-coated magnetic activated carbon. Appl. Catal. B Environ. 2012, 111–112, 246–253. [Google Scholar] [CrossRef]
- Mecha, A.C.; Onyango, M.S.; Ochieng, A.; Fourie, C.J.S.; Momba, M.N.B. Synergistic effect of UV-vis and solar photocatalytic ozonation on the degradation of phenol in municipal wastewater: A comparative study. J. Catal. 2016, 341, 116–125. [Google Scholar] [CrossRef]
- Li Puma, G.; Khor, J.N.; Brucato, A. Modeling of an Annular Photocatalytic Reactor for Water Purification: Oxidation of Pesticides. Environ. Sci. Technol. 2004, 38, 3737–3745. [Google Scholar] [CrossRef]
- Mena, E.; Rey, A.; Rodriguez, E.M.; Beltran, F.J. Nanostructured CeO2 as catalysts for different AOPs based in the application of ozone and simulated solar radiation. Catal. Today 2017, 280, 74–79. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Aguinaco, A.; García-Araya, J.F. Kinetic modelling of TOC removal in the photocatalytic ozonation of diclofenac aqueous solutions. Appl. Catal. B Environ. 2010, 100, 289–298. [Google Scholar] [CrossRef]
- Figueredo, M.; Rodríguez, E.M.; Rivas, F.J.; Beltrán, F.J. Kinetic model of ozone/light-based advanced oxidation processes: A pseudoempirical approach. Environ. Sci. Water Res. Technol. 2020, 6, 1176. [Google Scholar] [CrossRef]
- Tolosana-Moranchela, A.; Manassero, A.; Satuf, M.L.; Alfano, O.M.; Casas, J.A.; Bahamonde, A. TiO2-rGO photocatalytic degradation of an emerging pollutant: Kinetic modelling and determination of intrinsic kinetic parameters. J. Environ. Chem. Eng. 2019, 7, 103406. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Rey, A. Free radical and direct ozone reaction competition to remove priority and pharmaceutical water contaminants with single and hydrogen peroxide ozonation systems. Ozone Sci. Eng. 2018, 40, 1–15. [Google Scholar] [CrossRef]
- Beltrán, F.J. Ozone Reaction Kinetics for Water and Wastewater Systems; Lewis Publishers: Boca Raton, FL, USA, 2004; pp. 1–358. [Google Scholar]
- Charpentier, J.-C. Mass-transfer rates in gas-liquid absorbers and reactors. In Advances in Chemical Engineering; Academic Press: New York, NY, USA, 1981; Volume 11, pp. 1–133. [Google Scholar]
- Mvula, E.; von Sonntag, C. Ozonolysis of phenols in aqueous solution. Org. Biomol. Chem. 2003, 1, 1749–1756. [Google Scholar] [CrossRef]
- Leitzke, A.; von Sonntag, C. Ozonolysis of unsaturated acids in aqueous solution: Acrylic, methacrylic, maleic, fumaric and muconic acids. Ozone Sci. Eng. 2009, 31, 301–308. [Google Scholar] [CrossRef]
- Beltrán, F.J.; Encinar, J.M.; García-Araya, J.F. Modelling industrial wastewater ozonation in bubble contactors. 2: Scale-up from bench to pilot plant. Ozone Sci. Eng. 1995, 17, 379–398. [Google Scholar]
- Rey, A.; Mena, E.; Chávez, A.M.; Beltrán, F.J.; Medina, F. Influence of structural properties on the activity of WO3 catalysts for visible light photocatalytic ozonation. Chem. Eng. Sci. 2015, 126, 80–90. [Google Scholar] [CrossRef]
- Mena, E.; Rey, A.; Rodríguez, E.M.; Beltrán, F.J. Reaction mechanism and kinetics of DEET visible light assisted photocatalytic ozonation with WO3 catalyst. Appl. Catal. B Environ. 2017, 202, 460–472. [Google Scholar] [CrossRef]
- Chávez, A.M.; Ribeiro, A.R.; Moreira, N.F.; Silva, A.M.T.; Rey, A.; Álvarez, P.M.; Beltrán, F.J. Removal of Organic Micropollutants from a Municipal Wastewater Secondary Effluent by UVA-LED Photocatalytic Ozonation. Catalysts 2019, 9, 472. [Google Scholar] [CrossRef] [Green Version]
- Staehelin, S.; Hoigné, J. Decomposition of Ozone in Water the Presence of Organic Solutes Acting as Promoters and Inhibitors of Radical Chain Reactions. Environ. Sci. Technol. 1985, 19, 1206–1212. [Google Scholar] [CrossRef]
- Staehelin, S.; Hoigné, J. Decomposition of ozone in water: Rate of initiation by hydroxide ions and hydrogen peroxide. Environ. Sci. Technol. 1982, 16, 666–681. [Google Scholar] [CrossRef]
- Buxton, G.V.; Greenstock, C.L.; Helman, W.P.; Ross, A.B. Critical review of data constants for reactions of hydrated electrons, hydrogen atoms and hydroxyl radicals (OH/·O) in aqueous solution. J. Phys. Chem. Ref. Data 1988, 17, 513–886. [Google Scholar] [CrossRef] [Green Version]
- Christensen, H.S.; Sehensted, H.; Corfitzan, H. Reactions of hydroxyl radicals with hydrogen peroxide at ambient and elevated temperatures. J. Phys. Chem. 1982, 86, 55–68. [Google Scholar] [CrossRef]
- Weeks, J.L.; Rabani, J. The pulse radiolysis of dearated carbonate solutions. 1. Transient optical spectrum and mechanism. 2. pK for OH radicals. J. Phys. Chem. 1966, 82, 138–141. [Google Scholar]
- Cassano, A.E.; Alfano, O.M. Reaction engineering of suspended solid heterogeneous photocatalytic reactors. Catal. Today 2000, 58, 167–197. [Google Scholar] [CrossRef]
- Brucato, A.; Cassano, A.E.; Grisafi, F.; Montante, G.; Rizzuti, L.; Vella, G. Estimating radiant fields in flat heterogeneous photoreactors by the six-flux model. AIChE J. 2006, 52, 3882. [Google Scholar] [CrossRef]
- Zalazar, C.S.; Labas, M.D.; Martín, C.A.; Brandi, R.J.; Alfano, O.M.; Cassano, A.E. The extended use of actinometry in the interpretation of photochemical reaction engineering data. Chem. Eng. J. 2005, 109, 67–81. [Google Scholar] [CrossRef]
- Tolosana-Moranchela, A.; Manassero, A.; Satuf, M.L.; Alfano, O.M.; Casas, J.A.; Bahamonde, A. Influence of TiO2-rGO optical properties on the photocatalytic activity and efficiency to photodegrade an emerging pollutant. Appl. Catal. B Environ. 2019, 246, 1–11. [Google Scholar] [CrossRef]
- Li Puma, G.; Brucato, A. Dimensionless analysis of slurry photocatalytic reactors using two-flux and six-flux radiation absorption–scattering models. Catal. Today 2007, 122, 78–90. [Google Scholar] [CrossRef]
- Rice, R.G.; Do, D.D. Applied Mathematics and Modeling for Chemical Engineers; John Wiley & Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Sein, M.M.; Zedda, M.; Tuerk, J.; Schmidt, T.C.; Golloch, A.; von Sonntag, C. Oxidation of diclofenac with ozone in aqueous solution. Environ. Sci. Technol. 2008, 42, 6656–6662. [Google Scholar] [CrossRef]
- Rakowski, S.; Cherneva, D. Kinetics and mechanism of the reaction of ozone with aliphatic alcohols. Int. J. Chem. Kinet. 1990, 22, 321–329. [Google Scholar] [CrossRef]
- Tolosana-Moranchel, A.; Casas, J.A.; Carbajo, J.; Faraldos, M.; Bahamonde, A. Influence of TiO2 optical parameters in a slurry photocatalytic reactor: Kinetic modelling. Appl. Catal. B Environ. 2017, 200, 164–173. [Google Scholar] [CrossRef]
- Linsebigler, A.L.; Lu, G.; Yates, J.T., Jr. Photocatalysis on TiO2 surfaces: Principles, mechanisms and selected results. Chem. Rev. 1995, 95, 735–758. [Google Scholar] [CrossRef]
- Bader, H.; Hoigné, J. Determination of ozone in water by the indigo method. Water Res. 1981, 15, 449–456. [Google Scholar] [CrossRef]
- Masschelein, W.; Denis, M.; Ledent, R. Spectrophotometric determination of residual hydrogen peroxide. Water Sew. Work. 1977, 8, 69–72. [Google Scholar]
- Pastrana-Martínez, L.M.; Morales-Torres, S.; Likodimos, V.; Figueiredo, J.L.; Faria, J.L.; Falaras, P.; Silva, A.M.T. Advanced nanostructured photocatalysts based on reduced graphene oxide-TiO2 composites for degradation of diphenhydramine pharmaceutical and methyl orange dye. Appl. Catal. B Environ. 2012, 123–124, 241–256. [Google Scholar]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltrán, F.J.; Checa, M.; Rivas, J.; García-Araya, J.F. Modeling the Mineralization Kinetics of Visible Led Graphene Oxide/Titania Photocatalytic Ozonation of an Urban Wastewater Containing Pharmaceutical Compounds. Catalysts 2020, 10, 1256. https://doi.org/10.3390/catal10111256
Beltrán FJ, Checa M, Rivas J, García-Araya JF. Modeling the Mineralization Kinetics of Visible Led Graphene Oxide/Titania Photocatalytic Ozonation of an Urban Wastewater Containing Pharmaceutical Compounds. Catalysts. 2020; 10(11):1256. https://doi.org/10.3390/catal10111256
Chicago/Turabian StyleBeltrán, Fernando J., Manuel Checa, Javier Rivas, and Juan F. García-Araya. 2020. "Modeling the Mineralization Kinetics of Visible Led Graphene Oxide/Titania Photocatalytic Ozonation of an Urban Wastewater Containing Pharmaceutical Compounds" Catalysts 10, no. 11: 1256. https://doi.org/10.3390/catal10111256
APA StyleBeltrán, F. J., Checa, M., Rivas, J., & García-Araya, J. F. (2020). Modeling the Mineralization Kinetics of Visible Led Graphene Oxide/Titania Photocatalytic Ozonation of an Urban Wastewater Containing Pharmaceutical Compounds. Catalysts, 10(11), 1256. https://doi.org/10.3390/catal10111256