Modeling of Degradation of Diazo Dye in Swirl-Flow Photocatalytic Reactor: Response Surface Approach
Abstract
:1. Introduction
2. Results and Discussion
2.1. Selection of Optimal pH
2.2. RSM-CCD Model
2.3. Main Effect Plots
2.4. Validation and Verification of Model
Model Verification
2.5. Surface Response and Contour Plots
2.6. Mineralization of DB15 Dye
2.6.1. Influence of Initial Dye Concentration
2.6.2. Influence of Catalyst Concentration
3. Experimental
3.1. Chemicals and Catalysts
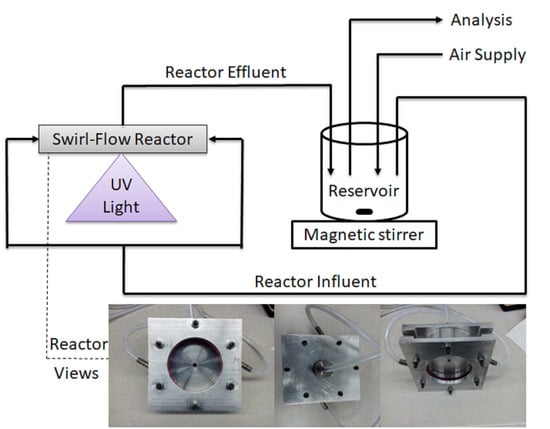
3.2. Experimental Setup
3.3. Experimental Procedure and Analytical Methods
3.4. Experimental Design
3.4.1. Selection Criteria of Parameters
3.4.2. Response Surface Methodology
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hu, J.; Men, J.; Liu, Y.; Huang, H.; Jiao, T. One-pot synthesis of Ag-modified LaMnO3–graphene hybrid photocatalysts and application in the photocatalytic discoloration of an azo-dye. RSC Adv. 2015, 5, 54028–54036. [Google Scholar] [CrossRef]
- An, C.; Peng, S.; Sun, Y. Facile synthesis of sunlight-driven AgCl: Ag plasmonic nanophotocatalyst. Adv. Mater. 2010, 22, 2570–2574. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Leung, Y.H.; Djurisic, A.B.; Ng, A.M.C.; Chan, W.K. Native defects in ZnO: Effect on dye adsorption and photocatalytic degradation. J. Phys. Chem. C 2013, 117, 12218–12228. [Google Scholar] [CrossRef]
- Wang, C.C.; Li, J.R.; Lv, X.L.; Zhang, Y.Q.; Guo, G. Photocatalytic organic pollutants degradation in metal–organic frameworks. Energy Environ. Sci. 2014, 7, 2831–2867. [Google Scholar] [CrossRef]
- Robinson, T.; McMullan, G.; Marchant, R.; Nigam, P. Remediation of dyes in textile effluent: A critical review on current treatment technologies with a proposed alternative. Bioresour. Technol. 2001, 77, 247–255. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, J. Adsorption study for removal of Congo red anionic dye using organo-attapulgite. Adsorption 2009, 15, 381–389. [Google Scholar] [CrossRef]
- Cerrón-Calle, G.A.; Aranda-Aguirre, A.J.; Luyo, C.; Garcia-Segura, S.; Alarcón, H. Photoelectrocatalytic decolorization of azo dyes with nano-composite oxide layers of ZnO nanorods decorated with Ag nanoparticles. Chemosphere 2019, 219, 296–304. [Google Scholar] [CrossRef]
- Guettai, N.; Amar, H.A. Photocatalytic oxidation of methyl orange in presence of titanium dioxide in aqueous suspension. Part II: Kinetics study. Desalination 2005, 185, 439–448. [Google Scholar] [CrossRef]
- Tabatabaee, M.; Roozbeh, M.; Roozbeh, M. Catalytic effect of lucunary heteropolyanion containing molybdenum and tungsten atoms on decolorization of direct blue 71. Chin. Chem. Lett. 2011, 22, 1501–1504. [Google Scholar] [CrossRef]
- Sleiman, M.; Vildozo, D.; Ferronato, C.; Chovelon, J.M. Photocatalytic degradation of azo dye Metanil Yellow: Optimization and kinetic modeling using a chemometric approach. Appl. Catal. B Environ. 2007, 77, 1–11. [Google Scholar] [CrossRef]
- Konstantinou, I.K.; Albanis, T.A. TiO2-assisted photocatalytic degradation of azo dyes in aqueous solution: Kinetic and mechanistic investigations: A review. Appl. Catal. B Environ. 2004, 49, 1–14. [Google Scholar] [CrossRef]
- Ramirez, J.H.; Maldonado-Hódar, F.J.; Pérez-Cadenas, A.F.; Moreno-Castilla, C.; Costa, C.A.; Madeira, L.M. Azo-dye Orange II degradation by heterogeneous Fenton-like reaction using carbon-Fe catalysts. Appl. Catal. B Environ. 2007, 75, 312–323. [Google Scholar] [CrossRef]
- Liu, T.; You, H.; Chen, Q. Heterogeneous photo-Fenton degradation of polyacrylamide in aqueous solution over Fe (III)–SiO2 catalyst. J. Hazard. Mater. 2009, 162, 860–865. [Google Scholar] [CrossRef] [PubMed]
- Brillas, E.; Martínez-Huitle, C.A. Decontamination of wastewaters containing synthetic organic dyes by electrochemical methods. An updated review. Appl. Catal. B Environ. 2015, 166, 603–643. [Google Scholar] [CrossRef]
- Santos, A.J.D.; de Lima, M.D.; da Silva, D.R.; Garcia-Segura, S.; Martínez-Huitle, C.A. Influence of the water hardness on the performance of electro-Fenton approach: Decolorization and mineralization of Eriochrome Black T. Electrochim. Acta 2016, 208, 156–163. [Google Scholar] [CrossRef]
- Li, R.; Song, X.; Huang, Y.; Fang, Y.; Jia, M.; Ma, W. Visible-light photocatalytic degradation of azo dyes in water by Ag3PO4: An unusual dependency between adsorption and the degradation rate on pH value. J. Mol. Catal. A Chem. 2016, 421, 57–65. [Google Scholar] [CrossRef]
- Hafshejani, M.K.; Ogugbue, C.J.; Morad, N.N. Application of response surface methodology for optimization of decolorization and mineralization of triazo dye Direct Blue 71 by Pseudomonas aeruginosa. 3 Biotech 2014, 4, 605–619. [Google Scholar] [CrossRef] [Green Version]
- Karamat, N.; Ehsan, M.F.; Ashiq, M.N.; Ijaz, S.; Najam-ul-Haq, M.; Hamid, S.; Bahnemann, D.W. Synthesis, characterization and photocatalytic activity of LaNdZr2O7 supported SnSe nanocomposites for the degradation of Foron blue dye. Appl. Surf. Sci. 2019, 463, 1019–1027. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, H. Optimization for decolorization of azo dye acid green 20 by ultrasound and H2O2 using response surface methodology. J. Hazard. Mater. 2009, 172, 1388–1393. [Google Scholar] [CrossRef]
- Demirel, M.; Kayan, B. Application of response surface methodology and central composite design for the optimization of textile dye degradation by wet air oxidation. Int. J. Ind. Chem. 2012, 3, 24. [Google Scholar] [CrossRef] [Green Version]
- Zinatizadeh, A.A.L.; Mohamed, A.R.; Abdullah, A.Z.; Mashitah, M.D.; Isa, M.H.; Najafpour, G.D. Process modeling and analysis of palm oil mill effluent treatment in an up-flow anaerobic sludge fixed film bioreactor using response surface methodology (RSM). Water Res. 2006, 40, 3193–3208. [Google Scholar] [CrossRef] [PubMed]
- Körbahti, B.K.; Aktaş, N.; Tanyolac, A. Optimization of electrochemical treatment of industrial paint wastewater with response surface methodology. J. Hazard. Mater. 2007, 148, 83–90. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, M.; Vahabzadeh, F.; Bonakdarpour, B.; Mofarrah, E.; Mehranian, M. Application of the central composite design and response surface methodology to the advanced treatment of olive oil processing wastewater using Fenton’s peroxidation. J. Hazard. Mater. 2005, 123, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Caliman, A.F.; Cojocaru, C.; Antoniadis, A.; Poulios, I. Optimized photocatalytic degradation of Alcian Blue 8 GX in the presence of TiO2 suspensions. J. Hazard. Mater. 2007, 144, 265–273. [Google Scholar] [CrossRef] [PubMed]
- Karacan, F.; Ozden, U.; Karacan, S. Optimization of manufacturing conditions for activated carbon from Turkish lignite by chemical activation using response surface methodology. Appl. Therm. Eng. 2007, 27, 1212–1218. [Google Scholar] [CrossRef]
- Lee, J.; Ye, L.; Landen, W.O., Jr.; Eitenmiller, R.R. Optimization of an extraction procedure for the quantification of vitamin E in tomato and broccoli using response surface methodology. J. Food Compos. Anal. 2000, 13, 45–57. [Google Scholar] [CrossRef]
- Somayajula, A.; Asaithambi, P.; Susree, M.; Matheswaran, M. Sonoelectrochemical oxidation for decolorization of Reactive Red 195. Ultrason. Sonochem. 2012, 19, 803–811. [Google Scholar] [CrossRef]
- Murugesan, K.; Dhamija, A.; Nam, I.H.; Kim, Y.M.; Chang, Y.S. Decolourization of reactive black 5 by laccase: Optimization by response surface methodology. Dyes Pigments 2007, 75, 176–184. [Google Scholar] [CrossRef]
- Li, X.; Jia, R.; Li, P.; Ang, S. Response surface analysis for enzymatic decolorization of Congo red by manganese peroxidase. J. Mol. Catal. B Enzym. 2009, 56, 1–6. [Google Scholar] [CrossRef]
- Bonyadinejad, G.; Sarafraz, M.; Khosravi, M.; Ebrahimi, A.; Taghavi-Shahri, S.M.; Nateghi, R.; Rastaghi, S. Electrochemical degradation of the Acid Orange 10 dye on a Ti/PbO2 anode assessed by response surface methodology. Korean J. Chem. Eng. 2016, 33, 189–196. [Google Scholar] [CrossRef]
- Ahmadi, S.; Mohammadi, L.; Igwegbe, C.A.; Rahdar, S.; Banach, A.M. Application of response surface methodology in the degradation of Reactive Blue 19 using H2O2/MgO nanoparticles advanced oxidation process. Int. J. Ind. Chem. 2018, 9, 241–253. [Google Scholar] [CrossRef] [Green Version]
- Tzikalos, N.; Belessi, V.; Lambropoulou, D. Photocatalytic degradation of Reactive Red 195 using anatase/brookite TiO2 mesoporous nanoparticles: Optimization using response surface methodology (RSM) and kinetics studies. Environ. Sci. Pollut. Res. 2013, 20, 2305–2320. [Google Scholar] [CrossRef] [PubMed]
- Salehi, K.; Bahmani, A.; Shahmoradi, B.; Pordel, M.A.; Kohzadi, S.; Gong, Y.; Lee, S.M. Response surface methodology (RSM) optimization approach for degradation of Direct Blue 71 dye using CuO–ZnO nanocomposite. Int. J. Environ. Sci. Technol. 2017, 14, 2067–2076. [Google Scholar] [CrossRef]
- Setarehshenas, N.; Hosseini, S.H.; Ahmadi, G. Optimization and Kinetic Model Development for Photocatalytic Dye Degradation. Arab. J. Sci. Eng. 2018, 43, 5785–5797. [Google Scholar] [CrossRef]
- Ray, A.K.; Beenackers, A.A. Novel swirl-flow reactor for kinetic studies of semiconductor photocatalysis. AIChE J. 1997, 43, 2571–2578. [Google Scholar] [CrossRef]
- Hashim, N.; Natarajan, P.; Ray, A.K. Intrinsic kinetic study for photocatalytic degradation of diclofenac under UV and visible light. Ind. Eng. Chem. Res. 2014, 53, 18637–18646. [Google Scholar] [CrossRef]
- Daneshvar, N.; Salari, D.; Khataee, A.R. Photocatalytic degradation of azo dye acid red 14 in water: Investigation of the effect of operational parameters. J. Photochem. Photobiol. A Chem. 2003, 157, 111–116. [Google Scholar] [CrossRef]
- Baran, W.; Adamek, E.; Makowski, A. The influence of selected parameters on the photocatalytic degradation of azo-dyes in the presence of TiO2 aqueous suspension. Chem. Eng. J. 2008, 145, 242–248. [Google Scholar] [CrossRef]
- Poulios, I.; Tsachpinis, I. Photodegradation of the textile dye Reactive Black 5 in the presence of semiconducting oxides. J. Chem. Technol. Biotechnol. Int. Res. Process Environ. Clean Technol. 1999, 74, 349–357. [Google Scholar] [CrossRef]
- Debnath, S.; Ballav, N.; Nyoni, H.; Maity, A.; Pillay, K. Optimization and mechanism elucidation of the catalytic photo-degradation of the dyes Eosin Yellow (EY) and Naphthol blue black (NBB) by a polyaniline-coated titanium dioxide nanocomposite. Appl. Catal. B Environ. 2015, 163, 330–342. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Xiang, L.; Huang, Q.; Qiu, J.; Zhang, H.; Valange, S. Heterogeneous photo-Fenton decolorization of Orange II over Al-pillared Fe-smectite: Response surface approach, degradation pathway, and toxicity evaluation. J. Hazard. Mater. 2015, 287, 32–41. [Google Scholar] [CrossRef] [PubMed]
- Ghaedi, A.M.; Karamipour, S.; Vafaei, A.; Baneshi, M.M.; Kiarostami, V. Optimization and modeling of simultaneous ultrasound-assisted adsorption of ternary dyes using copper oxide nanoparticles immobilized on activated carbon using response surface methodology and artificial neural network. Ultrason. Sonochem. 2019, 51, 264–280. [Google Scholar] [CrossRef] [PubMed]
- Jafari, M.; Rahimi, M.R.; Ghaedi, M.; Dashtian, K. ZnO nanoparticles loaded different mesh size of porous activated carbon prepared from Pinus eldarica and its effects on simultaneous removal of dyes: Multivariate optimization. Chem. Eng. Res. Des. 2017, 125, 408–421. [Google Scholar] [CrossRef]
- Bagheri, A.R.; Ghaedi, M.; Asfaram, A.; Hajati, S.; Ghaedi, A.M.; Bazrafshan, A.; Rahimi, M.R. Modeling and optimization of simultaneous removal of ternary dyes onto copper sulfide nanoparticles loaded on activated carbon using second-derivative spectrophotometry. J. Taiwan Inst. Chem. Eng. 2016, 65, 212–224. [Google Scholar] [CrossRef]
- So, C.M.; Cheng, M.Y.; Yu, J.C.; Wong, P.K. Degradation of azo dye Procion Red MX-5B by photocatalytic oxidation. Chemo 2002, 46, 905–912. [Google Scholar] [CrossRef]
- Stylidi, M.; Kondarides, D.I.; Verykios, X.E. Pathways of solar light-induced photocatalytic degradation of azo dyes in aqueous TiO2 suspensions. Appl. Catal. B Environ. 2003, 40, 271–286. [Google Scholar] [CrossRef]
- Habibi, M.H.; Hassanzadeh, A.; Mahdavi, S. The effect of operational parameters on the photocatalytic degradation of three textile azo dyes in aqueous TiO2 suspensions. J. Photochem. Photobiol. A Chem. 2005, 172, 89–96. [Google Scholar] [CrossRef]
- Lachheb, H.; Puzenat, E.; Houas, A.; Ksibi, M.; Elaloui, E.; Guillard, C.; Herrmann, J.M. Photocatalytic degradation of various types of dyes (Alizarin S, Crocein Orange G, Methyl Red, Congo Red, Methylene Blue) in water by UV-irradiated titania. Appl. Catal. B Environ. 2002, 39, 75–90. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, X.H.; Chan, K.C.; Liu, L.; Li, T. Fe-based metallic glass catalyst with nanoporous surface for azo dye degradation. Chemosphere 2017, 174, 76–81. [Google Scholar] [CrossRef]
- Vulliet, E.; Chovelon, J.M.; Guillard, C.; Herrmann, J.M. Factors influencing the photocatalytic degradation of sulfonylurea herbicides by TiO2 aqueous suspension. J. Photochem. Photobiol. A Chem. 2003, 159, 71–79. [Google Scholar] [CrossRef]
- O’Neill, C.; Hawkes, F.R.; Hawkes, D.L.; Lourenço, N.D.; Pinheiro, H.M.; Delée, W. Colour in textile effluents–sources, measurement, discharge consents and simulation: A review. J. Chem. Technol. Biotechnol. Int. Res. Process Environ. Clean Technol. 1999, 74, 1009–1018. [Google Scholar] [CrossRef]
- Stolz, A. Basic and applied aspects in the microbial degradation of azo dyes. Appl. Microbiol. Biotechnol. 2001, 56, 69–80. [Google Scholar] [CrossRef] [PubMed]
- Prevot, A.B.; Baiocchi, C.; Brussino, M.C.; Pramauro, E.; Savarino, P.; Augugliaro, V.; Palmisano, L. Photocatalytic degradation of acid blue 80 in aqueous solutions containing TiO2 suspensions. Environ. Sci. Technol. 2001, 35, 971–976. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, A.L.; Ismail, S.; Bhatia, S. Optimization of coagulation−flocculation process for palm oil mill effluent using response surface methodology. Environ. Sci. Technol. 2005, 39, 2828–2834. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Singh, L.; Dilbaghi, N. Optimization of process variables for decolorization of Disperse Yellow 211 by Bacillus subtilis using Box–Behnken design. J. Hazard. Mater. 2009, 164, 1024–1029. [Google Scholar] [CrossRef] [PubMed]
- Hou, P.; Cannon, F.S.; Nieto-Delgado, C.; Brown, N.R.; Gu, X. Effect of preparation protocol on anchoring quaternary ammonium/epoxide-forming compound into granular activated carbon for perchlorate adsorption: Enhancement by Response Surface Methodology. Chem. Eng. J. 2013, 223, 309–317. [Google Scholar] [CrossRef]
- Kumar, J.; Bansal, A. Photocatalytic degradation in annular reactor: Modelization and optimization using computational fluid dynamics (CFD) and response surface methodology (RSM). J. Environ. Chem. Eng. 2013, 1, 398–405. [Google Scholar] [CrossRef]
- Zuorro, A.; Fidaleo, M.; Lavecchia, R. Response surface methodology (RSM) analysis of photodegradation of sulfonated diazo dye Reactive Green 19 by UV/H2O2 process. J. Environ. Manag. 2013, 127, 28–35. [Google Scholar] [CrossRef]
- Sudarjanto, G.; Keller-Lehmann, B.; Keller, J. Optimization of integrated chemical–biological degradation of a reactive azo dye using response surface methodology. J. Hazard. Mater. 2006, 138, 160–168. [Google Scholar] [CrossRef]
- Moghaddam, S.S.; Moghaddam, M.A.; Arami, M. Coagulation/flocculation process for dye removal using sludge from water treatment plant: Optimization through response surface methodology. J. Hazard. Mater. 2010, 175, 651–657. [Google Scholar] [CrossRef]
- Li, H.; Gong, Y.; Huang, Q.; Zhang, H. Degradation of Orange II by UV-assisted advanced Fenton process: Response surface approach, degradation pathway, and biodegradability. Ind. Eng. Chem. Res. 2013, 52, 15560–15567. [Google Scholar] [CrossRef]
- Kayan, B.; Gözmen, B. Degradation of Acid Red 274 using H2O2 in subcritical water: Application of response surface methodology. J. Hazard. Mater. 2012, 201, 100–106. [Google Scholar] [CrossRef] [PubMed]
- Cho, I.H.; Zoh, K.D. Photocatalytic degradation of azo dye (Reactive Red 120) in TiO2/UV system: Optimization and modeling using a response surface methodology (RSM) based on the central composite design. Dyes Pigments 2007, 75, 533–543. [Google Scholar] [CrossRef]















| Coefficient | Type | Value |
|---|---|---|
| Constant term | 66.45 | |
| Linear term | 12.48 | |
| - | −14.67 | |
| - | 13.00 | |
| Quadratic term | −4.44 | |
| - | 4.01 | |
| - | −6.58 | |
| Cross product term | 4.22 | |
| - | 3.69 | |
| - | −0.36 |
| Parameter/Case | DF | Sum of Square | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 9 | 7340.67 | 815.63 | 59.71 | <0.0001 |
| Linear | 3 | 6479.23 | 2159.74 | 158.11 | <0.0001 |
| X1 | 1 | 1867.92 | 1867.92 | 136.75 | <0.0001 |
| X2 | 1 | 2583.80 | 2583.80 | 189.16 | <0.0001 |
| X3 | 1 | 2027.51 | 2027.51 | 148.43 | <0.0001 |
| Square | 3 | 608.40 | 202.80 | 14.85 | 0.002 |
| X11 | 1 | 137.56 | 146.83 | 10.75 | 0.014 |
| X22 | 1 | 148.07 | 119.86 | 8.77 | 0.021 |
| X33 | 1 | 322.76 | 322.76 | 23.63 | 0.002 |
| 2-Way Interaction | 3 | 253.04 | 84.35 | 6.17 | 0.022 |
| X1 X2 | 1 | 142.80 | 142.80 | 10.45 | 0.014 |
| X1 X3 | 1 | 109.22 | 109.22 | 8.00 | 0.025 |
| X2 X3 | 1 | 1.01 | 1.01 | 0.07 | 0.794 |
| Residual (error) | 7 | 95.62 | 13.66 | - | - |
| Lack-of-Fit | 5 | 72.27 | 14.45 | 1.24 | 0.503 |
| Pure Error | 2 | 23.35 | 11.67 | - | - |
| Total | 16 | 7436.28 | 815.63 | 59.71 | <0.0001 |
| Statistical summary of proposed model | |||||
| Std. Dev. | 3.70 | R-Squared | 98.71% | ||
| Mean | 61.51 | Adjusted R-squared | 97.06% | ||
| C.V. | 6.01 | Pred. R-Squared | 91.53% | ||
| PRESS | 630.16 | Adeq. Precision | 22.71 | ||
| Original Variables | Symbol | Unit | Coded Levels | ||||
|---|---|---|---|---|---|---|---|
| −1.41 | −1 | 0 | +1 | +1.41 | |||
| Catalyst concentration | X1 | g L−1 | 0.17 | 0.3 | 0.6 | 0.9 | 1.03 |
| Dye concentration | X2 | mg L−1 | 1.8 | 10 | 30 | 50 | 58.2 |
| Light intensity | X3 | W m−2 | 1 | 2.5 | 6.1 | 9.7 | 11.2 |
| Run Order | Standard Order | Coded Variables | Point Type | Decolorization Efficiency (%) | |||
|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | Experimental Y | Predicted Y | |||
| 1 | 3 | −1 | 1 | −1 | F. P | 21.87 | 19.12 |
| 2 | 6 | 1 | −1 | 1 | F. P | 95.62 | 99.42 |
| 3 | 1 | −1 | −1 | −1 | F. P | 54.47 | 56.18 |
| 4 | 7 | −1 | 1 | 1 | F. P | 37.09 | 37.02 |
| 5 | 17 | 0 | 0 | 0 | C. P | 66.24 | 66.45 |
| 6 | 11 | 0 | −1.414 | 0 | A. P | 100 | 95.21 |
| 7 | 2 | 1 | −1 | −1 | F. P | 64.2 | 65.32 |
| 8 | 13 | 0 | 0 | −1.414 | A. P | 34.82 | 34.91 |
| 9 | 8 | 1 | 1 | 1 | F. P | 78.5 | 77.8 |
| 10 | 12 | 0 | 1.414 | 0 | A. P | 51.05 | 53.72 |
| 11 | 5 | −1 | −1 | 1 | F. P | 74.82 | 75.52 |
| 12 | 10 | 1.414 | 0 | 0 | A. P | 78.04 | 75.22 |
| 13 | 14 | 0 | 0 | 1.414 | A. P | 73.91 | 71.68 |
| 14 | 16 | 0 | 0 | 0 | C. P | 68.89 | 66.45 |
| 15 | 4 | 1 | 1 | −1 | F. P | 44.79 | 45.14 |
| 16 | 9 | −1.414 | 0 | 0 | A. P | 39.25 | 39.93 |
| 17 | 15 | 0 | 0 | 0 | C. P | 62.11 | 66.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jadaa, W.; Prakash, A.; Ray, A.K. Modeling of Degradation of Diazo Dye in Swirl-Flow Photocatalytic Reactor: Response Surface Approach. Catalysts 2020, 10, 1418. https://doi.org/10.3390/catal10121418
Jadaa W, Prakash A, Ray AK. Modeling of Degradation of Diazo Dye in Swirl-Flow Photocatalytic Reactor: Response Surface Approach. Catalysts. 2020; 10(12):1418. https://doi.org/10.3390/catal10121418
Chicago/Turabian StyleJadaa, Waleed, Anand Prakash, and Ajay K. Ray. 2020. "Modeling of Degradation of Diazo Dye in Swirl-Flow Photocatalytic Reactor: Response Surface Approach" Catalysts 10, no. 12: 1418. https://doi.org/10.3390/catal10121418
APA StyleJadaa, W., Prakash, A., & Ray, A. K. (2020). Modeling of Degradation of Diazo Dye in Swirl-Flow Photocatalytic Reactor: Response Surface Approach. Catalysts, 10(12), 1418. https://doi.org/10.3390/catal10121418