Next Article in Journal
Organocatalysis: Fundamentals and Comparisons to Metal and Enzyme Catalysis
Next Article in Special Issue
Nature Inspired Solutions for Polymers: Will Cutinase Enzymes Make Polyesters and Polyamides Greener?
Previous Article in Journal
Carbon-Based Air-Breathing Cathodes for Microbial Fuel Cells
Previous Article in Special Issue
Mechanism-Guided Discovery of an Esterase Scaffold with Promiscuous Amidase Activity
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Catalysts
Volume 6
Issue 9
10.3390/catal6090129
catalysts-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Controlling Active Site Loop Dynamics in the (β/α)8 Barrel Enzyme Indole-3-Glycerol Phosphate Synthase

by
Kathleen F. O’Rourke
,
Aneta M. Jelowicki
and
David D. Boehr
*
Department of Chemistry, The Pennsylvania State University, University Park, PA 16802, USA
*
Author to whom correspondence should be addressed.
Catalysts 2016, 6(9), 129; https://doi.org/10.3390/catal6090129
Submission received: 9 June 2016 / Revised: 5 August 2016 / Accepted: 22 August 2016 / Published: 26 August 2016
(This article belongs to the Special Issue Enzyme Catalysis)
Browse Figures
Versions Notes

Abstract

:
The β1α1 loop in the tryptophan biosynthetic enzyme indole-3-glycerol phosphate synthase (IGPS) is important for substrate binding, product release and chemical catalysis. IGPS catalyzes the ring closure of the substrate 1-(o-carboxyphenylamine)-1-dexoyribulose 5-phosphate to form indole-3-glycerol phosphate, involving distinct decarboxylation and dehydration steps. The ring closure step is rate-determining in the thermophilic Sulfolobus sulfataricus enzyme (ssIGPS) at high temperatures. The β1α1 loop is especially important in the dehydration step as it houses the general acid Lys53. We propose that loop dynamics are governed by competing interactions on the N- and C-terminal sides of the loop. We had previously shown that disrupting interactions with the N-terminal side of the loop through the N90A substitution decreases catalytic efficiency, slows down the dehydration step and quenches loop dynamics on the picosecond to millisecond timescales. Here, we show that disrupting interactions on the C-terminal side of the loop through the R64A/D65A substitutions likewise decreases catalytic efficiency, slows down the dehydration step and quenches loop dynamics. Interestingly, the triple substitution R64A/D65A/N90A leads to new μs–ms timescale loop dynamics and makes the ring-closure step rate-determining once again. These results are consistent with a model in which the β1α1 loop is maintained in a structurally dynamic state by these competing interactions, which is important for the dehydration step of catalysis. Competing interactions in other enzymes may likewise keep their loops and other structural elements appropriately mobile.

Graphical Abstract

1. Introduction

Enzymes often undergo conformational changes as they bind substrate, perform chemical catalysis and release product. These conformational changes can often be classified as ‘domain motion’, where two rigid domains, joined by a flexible hinge, move relative to each other, or ‘loop motion’, where flexible surface loops fluctuate between different structures [1,2]. These conformational changes may be important for binding/release of substrate/products, reorientation of catalytic amino acid residues, removal of water from the active site and/or trapping of reactive intermediates [1,3]. The (β/α)8 barrel enzymes [4], including triose phosphate isomerase (TIM) [5,6] and indole-3-glycerol phosphate synthase (IGPS) [7], offer great examples where loop motions play important roles in enzyme catalysis. In TIM, loop closure excludes water from the active site [8,9,10,11,12], which is proposed to decrease the dielectric constant of the active site [13,14], such that the basicity of the active site glutamate [8,9,15,16] and other electrostatic interactions between polar side chains and the transition state are enhanced [13,14]. Similar effects are also likely important for IGPS catalysis. The motions of active site loops are often rate-determining [17,18,19,20,21]. For example, in the thermophilic Sulfolobus sulfataricus IGPS (ssIGPS) enzyme, product release is rate-determining at lower [22,23] but not at higher [24,25] temperatures likely because of the increased flexibility of the active site loops at elevated temperatures. Delineating the structural features that govern the motions of active site loops is thus important for understanding enzyme catalysis and kinetics. This knowledge may be leveraged towards improving and/or engineering new enzyme activities [26].
The (β/α)8 barrel is the most common protein fold in nature, comprising ~10% of enzymes with known structure [4]. Typical (β/α)8 proteins are 200 residues in length and consist of eight β-strand/α-helix units [4]. The β-strands form a parallel ring in the center of the enzyme, while the α-helices are arranged in a wheel on the outside [4] (Figure 1a). Loops that join β-strands to α-helices (i.e., βxαx loops, where x indicates the numbering of the β-strand/α-helix that are connected by the loop) often house catalytically important residues [4]. In ssIGPS, the most flexible loop is the β1α1 loop [22,27], which contains the general acid Lys53 [25] (Figure 1b).
We have proposed a revised chemical mechanism for IGPS [28], which overall catalyzes the ring closure of 1-(o-carboxyphenylamine)-1-dexoyribulose 5-phosphate (CdRP) into indole-3-glycerol phosphate (IGP) in the fifth step of the tryptophan biosynthetic pathway. In this revised mechanism (Figure 1c), Lys110 (numbering according to ssIGPS) acts a general acid to protonate the C2′ carbonyl of CdRP, facilitating ring closure and decarboxylation. Subsequently, Glu51 and Lys53 act as the general base and acid, respectively, in the dehydration step to produce IGP [25]. We have noted that following decarboxylation the intermediate must undergo a rearrangement in order to be properly positioned for dehydration [25]. Although X-ray crystal structures of ssIGPS [25,28] indicate that there is ample room within the active site to accommodate such a rearrangement, motions of ssIGPS, including those of the β1α1 loop, may facilitate this process. The β1α1 loop is thus involved in most stages of ssIGPS catalysis, from substrate binding to chemical catalysis, and finally to product release.
We have also previously shown that interactions with the nearby β2α2 loop help to govern β1α1 loop dynamics and ssIGPS function [29]. Combined statistical coupling analysis (SCA) and molecular dynamics (MD) simulations had suggested that interactions between the two loops might be important for the function and structure of IGPS [27]. In particular, our experimental studies indicated that the interactions between Arg54 on the β1α1 loop and Asn90 on the β2α2 loop are important for β1α1 loop dynamics and ssIGPS catalysis [29]. For instance, the N90A substitution resulted in a modest decrease in the steady-state kinetic parameters, a different rate-determining step than wild-type (WT) enzyme, and a decrease in the μs-ms timescale motions of the β1α1 loop according to nuclear magnetic resonance (NMR) relaxation studies [29]. Surprisingly, severing this interaction between the β1α1 and β2α2 loops also led to an increase in protein stability, as measured by a two-fold decrease in the thermal inactivation rate of the N90A variant compared to the WT enzyme [29].
The results with the N90A variant appeared to be counterintuitive, considering that breaking interactions with the β1α1 loop decreased loop flexibility and increased protein stability. We suggested that there are other interactions that may influence the conformational dynamics of the β1α1 loop [29]. In particular, we noted that there is a hydrogen bond network involving Arg64 and Asp65 on the β1α1 loop, Ile67, Glu68 and Tyr69 on the α1 helix, and Met237 and Arg238 on the α8’ helix. The α8’ helix is an additional helix compared to the canonical (β/α)8 barrel fold. We proposed that competing interactions on the N-terminal (e.g., the interaction between Arg54-Asn90) and C-terminal (e.g., interactions between Arg64/Asp65 and residues on the α1 and α8’ helices) sides of the β1α1 loop help to govern its structural dynamics (Figure 1b), affecting its many roles in ssIGPS catalysis. In other words, the β1α1 loop may be unable to interact simultaneously with the β2α2 loop and the α1/α8’ helices, but instead fluctuates or toggles between favoring interactions on either side of the loop. Disruption of one set of interactions would lead to continuous interactions with the remaining set of interactions and an overall loss of loop motion.
In this manuscript, we demonstrate that indeed severing the interactions with the α1/α8’ helices through the R64A/D65A double substitution decreases β1α1 loop motions and changes the identity of the rate-determining step of ssIGPS catalysis, similar to the N90A substitution. Severing both sets of interactions through the R54A/D65A/N90A triple substitution leads to new μs–ms timescale motions to the β1α1 loop and results in the same rate-determining step as WT enzyme. The structural dynamics of catalytically important active site loops in other enzymes may likewise be governed by competing interactions to keep these loops in conformationally “frustrated” states [30].

2. Results

2.1. Severing Interactions with the C-Terminal Side of the β1α1 Loop Results in Modest Decreases in Steady-State Kinetics

To probe the effects of disrupting the interactions on the C-terminal side of the β1α1 loop, we tested the R64A/D65A double variant. This double variant should disrupt the hydrogen bonding network formed between the β1α1 loop and the α1 and α8′ helices (Figure 1b). Since both positions are changed to Ala, the overall charge on the variant enzyme should be very similar to WT enzyme, and so changes to the electrostatic interactions of the enzyme should be of less concern.
The R64A/D65A double substitution led to a modest two-fold decrease in the catalytic turnover rate constant (kcat) and a four-fold decrease in the second-order rate constant (kcat/KM) at 37 °C compared to WT enzyme (Table 1), similar to the kinetic changes previously reported for the N90A variant [29]. We also performed assays at 75 °C, which is closer to the physiological temperature of S. sulfataricus [31]. At the higher temperature, there was only a minor change in kcat, but a much larger eight-fold decrease in kcat/KM, owing to an elevated KM (Table 1). The elevated KM for the R64A/D65A variant may reflect a change in substrate binding, due to changes in the structural dynamics of the β1α1 loop. Solvent viscosity effects (SVE; slope of a plot of relative rate vs. relative viscosity) also report indirectly on ligand binding on/off rates. For instance, WT enzyme has a substantial SVE at 37 °C, which is likely due to IGP release being partly rate limiting [24]. For the R64A/D65A variant, the SVE approaches zero at both temperatures, indicating that IGP release is no longer rate limiting, perhaps due to an increased product off-rate.

2.2. Severing Interactions with the C-Terminal Side of the β1α1 Loop Changes the Identity of the Rate-Determining Step

We have previously noted that the identity of the rate-determining step for ssIGPS can change depending on temperature [24] and amino acid substitutions [25,29]. Such a change in the identity of the rate-determining step implies that the steady-state kinetic parameters underreport changes to the underlying microscopic rate constants. We have previously described the use of SVEs and solvent deuterium kinetic isotope effects (SDKIE = kcat,H2O/kcat,D2O) to gain insight into the identity of the rate-determining step of ssIGPS catalysis [24,25]. Such studies are important considering that pre-steady state kinetics was unable to resolve individual microscopic rate constants for the chemical steps [22]. If the rate-determining step is either binding of CdRP or release of IGP, then we expect kcat to be dependent on solvent viscosity, whereas chemical steps should be independent of solvent viscosity (Figure 2). The step involving the protonation of CdRP by Lys110 is solvent isotope sensitive, but the remaining steps will be insensitive [25]. For WT ssIGPS at 25 °C, the rate-determining step is the release of IGP product [22], and so, the SVE approaches a theoretical maximum of 1, and there is no SDKIE (SDKIE = 1) [24]. At 75 °C, WT ssIGPS has SVE ~0 and SDKIE ~4, suggesting that the rate-determining step is ring closure/decarboxylation [24,25].
For the R64A/D65A variant, the SVE approached zero and there was no SDKIE (~1) at 75 °C. These results are similar to those for the N90A variant [29]. These results suggest that the rate-determining step is dehydration for these variants. The dehydration step involves acid-base catalysis by Lys53 in the β1α1 loop and Glu51 in the adjacent β1 strand. The R64A/D65A and N90A substitutions likely perturb the structure and/or motions of the β1α1 loop and β1 strand, such that the dehydration step is sufficiently slowed to become at least partially rate-determining.

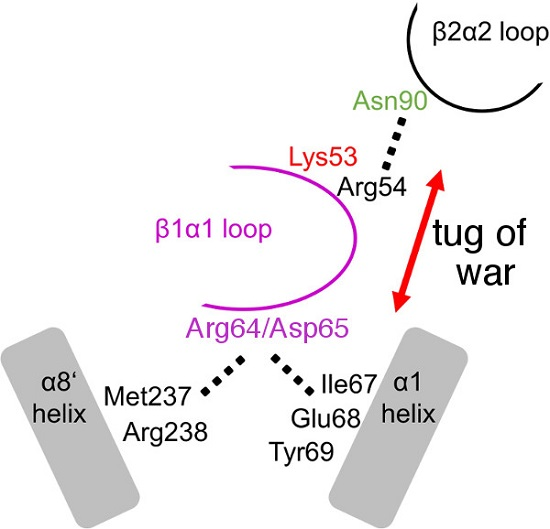
2.3. The R64A/D65A and N90A Substitutions Perturb the Structure of the β1α1 Loop in Different Ways

To gain insight into how the R64A/D65A substitutions may affect ssIGPS structure and stability, we performed thermal inactivation studies. In these assays, enzyme was incubated at 90 °C and aliquots were removed at various time points and assayed at 50 °C. The thermal inactivation rate was determined from a linear fit of the activity of each aliquot as a function of incubation time. The R64A/D65A substitutions induced a five-fold increase in the thermal inactivation rate compared to WT enzyme (Table 1). This result is strikingly different from results previously reported for the N90A variant, which indicated that the N90A variant was more thermostable than WT enzyme [29]. Part of the difference may be because the N90A substitution disrupts interactions between two flexible loops, but the R64A/D65A substitutions disrupt interactions between the β1α1 loop and the α1/α8’ helices. This hydrogen-bonding network between the loop and helices may be important for thermal stability.
To gain more insight into how the R64A/D65A substitutions may affect the structure and/or internal motions of ssIGPS, we compared circular dichroism (CD) and NMR spectra between the R64A/D65A variant and WT ssIGPS. The CD spectrum of the R64A/D65A variant was very similar to that of WT ssIGPS (Figure 3a), where the ratios of α-helix to β-strand structure were nearly identical. The 1H-15N HSQC (heteronuclear single quantum coherence) spectrum of the R64A/D65A variant was also very similar to that of the WT enzyme (Figure 3b). Nonetheless, there were some major chemical shift perturbations as a result of the R64A/D65A substitutions, including to the 1H-15N backbone amide resonances of β1α1 loop residues Lys53, Arg54, Lys55 and Ser56 (Figure 3b). It should be noted that these chemical shift perturbations were generally in different directions and of different magnitudes than those perturbations induced by the N90A substitution (Figure 3b). These results imply that the N90A and R64A/D65A substitutions perturbed the structure of the β1α1 loop in different ways.

2.4. Severing Interactions with the C-Terminal Side of the β1α1 Loop Quenches μs–ms Timescale Loop Motions

NMR experiments can also provide insight into the structural dynamics of proteins over a wide-range of timescales [17,18,21]. We determined Rex values (Figure 4a), the contribution of conformational exchange on the μs-ms timescale to the R2 transverse relaxation rates. We note that most of the residues colored blue in Figure 4a had Rex values approaching zero, and none had Rex values greater than 1.8 s−1. We only viewed Rex values greater than 3 s−1 to be associated with substantial μs–ms timescale motions. We also note that Rex is not simply the rate constant for motion, but is also dependent on other factors (e.g., populations of the exchanging conformations [32]). There were only 2–3 residues that were associated with Rex values above 3 s−1, however this is not unusual as loops in other enzymes (e.g., dihydrofolate reductase [33]) thought to have significant μs–ms timescale motions may also only have a few residues that are associated with significant Rex values. Finally, it should be kept in mind, that the presence of substrates, intermediates or products can substantially change loop motions.
We also measured 1H-15N heteronuclear Overhauser effects (hetNOEs) (Figure 4b), which provide a qualitative estimate of motions on the ps–ns timescale, as they roughly correlate with the backbone S2 order parameter. HetNOEs ranged from 0.6 to ~1, where lower (higher) values correlate to higher (lower) amplitude ps-ns timescale dynamics.
We had previously shown that the N90A substitution leads to a loss of conformational exchange events on the μs–ms timescale (i.e., Rex ~ 0), and less ps-ns timescale motions (i.e., hetNOEs for N90A ssIGPS were generally higher than hetNOEs for WT ssIGPS; also see Figure 4) [29]. Similar results were observed for the R64A/D65A variant (Figure 4). These results indicate that severing interactions on either the N-terminal or C-terminal side of the β1α1 loop led to a quenching of the ps–ns and μs–ms timescale loop motions.

2.5. Severing Interactions with Both the N-Terminal and C-Terminal Sides of the β1α1 Loop Results in a Rate-Determining Step Similar to Wild-Type Enzyme

We proposed that the β1α1 loop fluctuates between making stronger interactions with the β2α2 loop and making stronger interactions with the α1/α8’ helices; these competing interactions contribute to the structural dynamics of the β1α1 loop. Consistent with this proposal, we have now shown that disrupting either set of interactions results in structural and dynamic changes to the β1α1 loop (Figure 3 and Figure 4), such that the dehydration step becomes rate-determining in both cases (Figure 2). To better understand the role(s) of these competing interactions to the structure, dynamics and function of ssIGPS, we also analyzed the R64A/D65A/N90A triple variant, where these substitutions should disrupt the β1α1 loop interactions with both the β2α2 loop and the α1/α8’ helices.
The R64A/D65A/N90A substitutions decreased both kcat and kcat/KM steady-state kinetic parameters (Table 1). The changes in kcat were of similar magnitude to those previously determined for the N90A variant [29], and the changes in KM were of similar magnitude to those determined for the R64A/D65A variant (Table 1). To better understand the effects of combining the N90A and R64A/D65A substitutions, we also determined the free energy changes induced on the catalytic efficiency of the enzyme (i.e., ΔΔG = −RT ln ((kcat/KM)variant/(kcat/KM)WT) (Figure 5). The thermodynamic effects are predicted to be additive (i.e., ΔΔG (R64A/D65A/N90A) = ΔΔG (R64A/D65A) + ΔΔG (N90A)) if changes on the N-terminal and C-terminal sides of the β1α1 loop are independent [34,35]. Our calculations indicated that the R64A/D65A/N90A triple variant had a free energy change (1.77 kcal/mol) that was less than the addition of the free energies for the N90A single variant (0.71 kcal/mol) and R64A/D65A double variant (1.54 kcal/mol) at 75 °C; similar results were also determined at 37 °C (Figure 5). These results suggest that the H-bonding networks on the N-terminal and C-terminal sides of the β1α1 loop are weakly dependent in regards to catalysis. The thermal inactivation rate constant for the R64A/D65A/N90A triple variant was also similar to that of the R64A/D65A double variant, indicating that the N90A substitution had no additional effect on protein thermal stability within the context of the R64A/D65A substitutions (Table 1).
We also determined the SVE and SDKIE for the R64A/D65A/N90A triple variant to gain insight into the identity of the rate-determining step. With this variant, there was no SVE, but there was a substantial SDKIE (Table 1), suggesting that the rate-determining step was ring closure/decarboxylation (Figure 2), similar to results with the WT enzyme but different from results with either the N90A single variant or the R64A/D65A double variant.

2.6 Severing Interactions with Both the N-Terminal and C-Terminal Sides of the β1α1 Loop Results in New μs–ms Timescale Loop Dynamics

Our results with the N90A and R64A/D65A variants indicated that disrupting interactions with the N- or C-terminal sides of the β1α1 loop diminished both μs–ms and ps–ns timescale dynamics (Figure 4). In contrast, disrupting both sets of interactions through the R64A/D65A/N90A triple substitution led to new μs–ms timescale dynamics in the β1α1 loop (Figure 4a), although there was additional ordering on the ps–ns timescale (Figure 4b). In WT enzyme, Lys55 and Ser56 have Rex values between 7 and 8 s−1, whereas these residues were associated with Rex values less than 1 s−1 in the R64A/D65A/N90A triple variant. In contrast, Gly59 was associated with an Rex value slightly less than 5 s−1 and Leu60 was associated with an Rex value ~3 s−1 for the R64A/D65A/N90A triple variant, but there were not substantial Rex values for these residues in the WT enzyme.

3. Discussion

The motion of active-site loops is important for the function of a large variety of enzymes, including classic examples, such as TIM [5], HIV protease [36], fructose-1,6-bisphosphate aldolase [37], lipase [38], enolase [39,40], protein kinases [41] and dihydrofolate reductase (DHFR) [42]. These motions may be important in gating the entry and exit of substrate and products, and creating microenvironments conducive to chemical catalysis. Importantly, many of these loop motions are rate-determining [17,18,21]. Considering their functional importance, understanding and controlling active-site loop motions may be necessary in the design and engineering of next generation enzyme catalysts [26].
We have shown in this manuscript that the structural dynamics of the β1α1 active-site loop in ssIGPS is controlled in part by interactions on the N- and C-terminal sides of the loop (Figure 1). Our previous experiments indicated that Asn90 on the β2α2 loop helps to modulate the structural dynamics of the β1α1 loop and ssIGPS function [29]. These results are reminiscent of previous MD simulations of β1,4-galactosyltransferase, enolase and lipase enzymes that suggested interactions with smaller loops help to gate the structural dynamics of larger active-site loops [43,44]. In TIM, there are catalytically essential hydrogen bond interactions between the β6α6 active-site loop and the nearby β7α7 loop [45,46]. Disrupting these interactions also led to motional changes to the active-site loop and decreased catalytic activity [47,48].
It was initially surprising that the N90A substitution led to decreased β1α1 loop flexibility and a more thermally stable enzyme, although we had noted that interactions with the α1/α8’ helices may also modulate β1α1 loop dynamics [29]. We have shown in this manuscript that the R64A/D65A substitutions that disrupt the hydrogen-bonding network between the β1α1 loop and α1/α8’ helices also lead to decreased catalytic efficiency (Table 1), a change in the identity of the rate-determining step (Figure 2), and a quenching of the ps–ns and μs–ms timescale dynamics of the β1α1 loop (Figure 4), similar to the N90A variant [29]. One potential weakness of this study was that substitutions on the β1α1 loop itself may affect loop motions, regardless of the disruption of interactions with the α1/α8’ helices. To disentangle these effects, future work may address studies of α1/α8’ variants.
In the R64A/D65A/N90A triple variant, the rate-determining step was returned to that of the WT enzyme (Figure 2) and new μs–ms timescale dynamics were induced (Figure 4). Functional changes must be primarily due to local changes to the β1α1 loop, considering that any major chemical shift changes were localized to this loop (Figure 3). It should be kept in mind that the R64A/D65A/N90A triple variant was still more catalytically impaired than either the N90A single variant or R64A/D65A double variant (Figure 5). These results also establish a connection between the catalytic efficiency of the dehydration step and the structural dynamics of the β1α1 loop. The structure/dynamics of the β1α1 loop may modulate the positioning and/or chemical environment of the Lys53 general acid and Glu51 general base, or even be involved in the rearrangement of the intermediate we had suggested previously [25] (Figure 1).
We propose that there is a “tug-of-war” between the β1α1/β2α2 loop interactions and the β1α1/α1/α8’ interactions such that the β1α1 loop fluctuates between conformations favoring each of these sets of interactions. Disrupting either set of interactions quenches the μs–ms timescale dynamics and slows the dehydration step sufficiently such that it becomes rate-determining. In the R64A/D65A/N90A variant, the β1α1 loop is no longer restricted by either set of interactions and is free to fluctuate into alternative conformations, as shown by the new Rex values (Figure 4). These alternative conformations may more appropriately arrange Glu51 and Lys53, such that the dehydration step is not rate-determining. This idea of competing interactions is also known as “protein frustration” [30] and may be generally important for maintaining functional dynamics of active-site loops. A similar example is found in the E. coli DHFR enzyme, in which the FG and GH loops compete for interactions with the active-site Met20 loop [49]. Amino acid substitutions in either the FG and GH loops that disrupt these interactions lead to decreases in catalytic efficiency [50,51,52] and changes to the μs–ms timescale Met20 loop dynamics [53,54,55].
Loop dynamics may also be altered by changing loop residues not directly involved with interactions with other protein structural elements (e.g., [56]), or through whole loop swaps (e.g., [48]). These various strategies offer ways of controlling loop dynamics to provide insights into the relationships between protein structural dynamics and enzyme catalysis. This understanding of loop dynamics can be leveraged towards the development of enzyme catalysts with different catalytic rates, substrate specificities and even new chemistries.

4. Materials and Methods

4.1. Site-Directed Mutagenesis, Overexpression, and Purification of ssIGPS Variants

The R64A/D65A and R64A/D65A/N90A ssIGPS variants were generated using the QuikChange Lightning site-directed mutagenesis kit (Agilent Technologies, Santa Clara, CA, USA) with primers from the Nucleic Acid Facility at the Pennsylvania State University. All variants and wild type plasmids were confirmed through DNA sequencing performed at the same Nucleic Acid Facility (State College, PA, USA). All variants were overexpressed using Escherichia coli BL21(DE3)* cells and purified with Ni NTA agarose resin, as described previously [7,24]. Samples used for kinetic and CD studies were grown in Luria-Bertani media and samples used for NMR studies were grown in M9 minimal media using 15N-labeled ammonium chloride.

4.2. Steady-State Kinetic Enzyme Assays

Steady-state kinetic assays for ssIGPS were performed by measuring IGP accumulation through fluorescence [24,57]. The excitation and emission wavelengths were 278 and 340 nm, respectively. Initial rates were fit to the Michaelis-Menten equation (Equation (1)) to yield kcat and KM values:
v = [ S ] / ( K M + [ S ] )
where v is the initial reaction velocity, ET is the total enzyme concentration and [S] is the substrate concentration.
In order to interrogate the solvent viscosity effect (SVE), reactions at saturating CdRP concentrations were performed in assay buffer (50 mM HEPPS, 4 mM EDTA, pH 7.5) containing 0%–30% (w/v) of microviscogen (glycerol or sucrose). The relative viscosity of each solution was determined using an Ostwald viscometer. The SVE were determined by plotting the relative rate (vi/vviscogen) against the relative viscosity.
The solvent deuterium kinetic isotope effect (SDKIE) was determined at saturating CdRP concentrations (i.e., [CdRP] > 5 × KM) in assay buffer made with D2O. pD values were determined through measurement of the pH (pD = pH + 0.4). The SDKIE was defined as kobs,H2O/kobs,D2O.

4.3. Thermal Inactivation and Circular Dichroism Spectroscopy

ssIGPS variants were incubated at 90 °C for varying amounts of time, up to 20 min. Rates were measured under saturating CdRP conditions (i.e., [CdRP] > 5 × KM) at 50 °C. Inactivation rates were found by fitting the relative rate of reaction versus the time of incubation.
The overall folds of the ssIGPS variants were checked using a CD spectrometer (State College, PA, USA). All samples were diluted to 1.5 M and measured in 10 mM potassium phosphate buffer (pH 7.0) from 280–190 nm at 25 °C.

4.4. NMR Experiments

All NMR data was collected using a Brüker (Billerica, MA, USA) Avance III 600 MHz spectrometer at 310 K, using 1 mM protein in 25 mM potassium phosphate pH 7.0, 75 mM KCl, 1 mM EDTA, 1 mM DTT, 0.02% NaN3, and 10% (v/v) 2H2O. 1H-15N hetNOE values were calculated by collecting two pairs of spectra with and without proton saturation in an interleaved manner. R2 relaxation was measured using previously described constant-time relaxation-compensated CPMG (Carr-Purcell-Meiboom-Gill) pulse sequences [58,59]. The effective R2 relaxation was calculated from the equation R2eff = (−ln(I(υCPMG)/I(0))/T with T being the total relaxation period (40 ms) during CPMG pulsing, I(0) being the reference intensity without CPMG pulsing, and υCPMG being 1/τ, the inverse of the duration between 180° pulses. Rex, the contribution of conformational change to R2, was estimated by the difference between R2effwith slow pulsing (υCPMG = 100 s−1) and fast pulsing (υCPMG = 2000 s−1).

Acknowledgments

We would like to thank Alyson Boehr and Rebecca D’Amico for their helpful comments on this manuscript. This research was financially supported by NSF Career Grant MCB1053993.

Author Contributions

K.F.O. and D.D.B. conceived and designed the experiments; K.F.O. and A.M.J. performed the experiments; K.F.O., A.M.J. and D.D.B. analyzed the data; K.F.O. and D.D.B. wrote the paper.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

The following abbreviations are used in this manuscript:
TIMtriose phosphate isomerase
IGPSindole-3-glycerol phosphate synthase
ssIGPSindole-3-glycerol phosphate synthase from Sulfolobus sulfataricus
CdRP1-(o-carboxyphenylamine)-1-dexoyribulose 5-phosphate
IGPindole-3-glycerol phosphate
SCAstatistical coupling analysis
MDmolecular dynamics
WTwild-type
NMRnuclear magnetic resonance
SVEsolvent viscosity effect
SDKIEsolvent deuterium kinetic isotope effect
CDcircular dichroism
HSQCheteronuclear single quantum coherence
hetNOEheteronuclear Overhauser effect
DHFRdihydrofolate reductase

References

  1. Gutteridge, A.; Thornton, J. Conformational change in substrate binding, catalysis and product release: An open and shut case? FEBS Lett. 2004, 567, 67–73. [Google Scholar] [CrossRef] [PubMed]
  2. Kempner, E.S. Movable lobes and flexible loops in proteins. Structural deformations that control biochemical activity. FEBS Lett. 1993, 326, 4–10. [Google Scholar] [CrossRef]
  3. Hammes, G.G. Multiple conformational changes in enzyme catalysis. Biochemistry 2002, 41, 8221–8228. [Google Scholar] [CrossRef] [PubMed]
  4. Sterner, R.; Hocker, B. Catalytic versatility, stability, and evolution of the (βα)8-barrel enzyme fold. Chem. Rev. 2005, 105, 4038–4055. [Google Scholar] [CrossRef] [PubMed]
  5. Richard, J.P. A paradigm for enzyme-catalyzed proton transfer at carbon: Triosephosphate isomerase. Biochemistry 2012, 51, 2652–2661. [Google Scholar] [CrossRef] [PubMed]
  6. Malabanan, M.M.; Nitsch-Velasquez, L.; Amyes, T.L.; Richard, J.P. Magnitude and origin of the enhanced basicity of the catalytic glutamate of triosephosphate isomerase. J. Am. Chem. Soc. 2013, 135, 5978–5981. [Google Scholar] [CrossRef] [PubMed]
  7. Hennig, M.; Darimont, B.; Sterner, R.; Kirschner, K.; Jansonius, J.N. 2.0 A structure of indole-3-glycerol phosphate synthase from the hyperthermophile Sulfolobus solfataricus: Possible determinants of protein stability. Structure 1995, 3, 1295–1306. [Google Scholar] [CrossRef]
  8. Alahuhta, M.; Wierenga, R.K. Atomic resolution crystallography of a complex of triosephosphate isomerase with a reaction-intermediate analog: New insight in the proton transfer reaction mechanism. Proteins 2010, 78, 1878–1888. [Google Scholar] [CrossRef] [PubMed]
  9. Kursula, I.; Wierenga, R.K. Crystal structure of triosephosphate isomerase complexed with 2-phosphoglycolate at 0.83-Å resolution. J. Biol. Chem. 2003, 278, 9544–9551. [Google Scholar] [CrossRef] [PubMed]
  10. O’Donoghue, A.C.; Amyes, T.L.; Richard, J.P. Hydron transfer catalyzed by triosephosphate isomerase. Products of isomerization of (R)-glyceraldehyde 3-phosphate in D2O. Biochemistry 2005, 44, 2610–2621. [Google Scholar] [CrossRef] [PubMed]
  11. O’Donoghue, A.C.; Amyes, T.L.; Richard, J.P. Slow proton transfer from the hydrogen-labelled carboxylic acid side chain (Glu-165) of triosephosphate isomerase to imidazole buffer in D2O. Org. Biomol. Chem. 2008, 6, 391–396. [Google Scholar] [CrossRef] [PubMed]
  12. O’Donoghue, A.C.; Amyes, T.L.; Richard, J.P. Hydron transfer catalyzed by triosephosphate isomerase. Products of isomerization of dihydroxyacetone phosphate in D2O. Biochemistry 2005, 44, 2622–2631. [Google Scholar] [CrossRef] [PubMed]
  13. Richard, J.P.; Amyes, T.L.; Goryanova, B.; Zhai, X. Enzyme architecture: On the importance of being in a protein cage. Curr. Opin. Chem. Biol. 2014, 21, 1–10. [Google Scholar] [CrossRef] [PubMed]
  14. Malabanan, M.M.; Amyes, T.L.; Richard, J.P. A role for flexible loops in enzyme catalysis. Curr. Opin. Struct. Biol. 2010, 20, 702–710. [Google Scholar] [CrossRef] [PubMed]
  15. Lolis, E.; Petsko, G.A. Crystallographic analysis of the complex between triosephosphate isomerase and 2-phosphoglycolate at 2.5-Å resolution: Implications for catalysis. Biochemistry 1990, 29, 6619–6625. [Google Scholar] [CrossRef] [PubMed]
  16. Richard, J.P.; Amyes, T.L.; Malabanan, M.M.; Zhai, X.; Kim, K.J.; Reinhardt, C.J.; Wierenga, R.K.; Drake, E.J.; Gulick, A.M. Structure-function studies of hydrophobic residues that clamp a basic glutamate side chain during catalysis by triosephosphate isomerase. Biochemistry 2016, 55, 3036–3047. [Google Scholar] [CrossRef] [PubMed]
  17. Loria, J.P.; Berlow, R.B.; Watt, E.D. Characterization of enzyme motions by solution NMR relaxation dispersion. Acc. Chem. Res. 2008, 41, 214–221. [Google Scholar] [CrossRef] [PubMed]
  18. Palmer, A.G., 3rd. Enzyme dynamics from NMR spectroscopy. Acc. Chem. Res. 2015, 48, 457–465. [Google Scholar] [CrossRef] [PubMed]
  19. Rozovsky, S.; McDermott, A.E. The time scale of the catalytic loop motion in triosephosphate isomerase. J. Mol. Biol. 2001, 310, 259–270. [Google Scholar] [CrossRef] [PubMed]
  20. Whittier, S.K.; Hengge, A.C.; Loria, J.P. Conformational motions regulate phosphoryl transfer in related protein tyrosine phosphatases. Science 2013, 341, 899–903. [Google Scholar] [CrossRef] [PubMed]
  21. Lisi, G.P.; Loria, J.P. Using NMR spectroscopy to elucidate the role of molecular motions in enzyme function. Prog. Nucl. Mag. Res. Spectrosc. 2016, 92–93, 1–17. [Google Scholar] [CrossRef] [PubMed]
  22. Schlee, S.; Dietrich, S.; Kurcon, T.; Delaney, P.; Goodey, N.M.; Sterner, R. Kinetic mechanism of indole-3-glycerol phosphate synthase. Biochemistry 2012, 52, 132–142. [Google Scholar] [CrossRef] [PubMed]
  23. Merz, A.; Yee, M.C.; Szadkowski, H.; Pappenberger, G.; Crameri, A.; Stemmer, W.P.C.; Yanofsky, C.; Kirschner, K. Improving the catalytic activity of a thermophilic enzyme at low temperatures. Biochemistry 2000, 39, 880–889. [Google Scholar] [CrossRef] [PubMed]
  24. Zaccardi, M.J.; Mannweiler, O.; Boehr, D.D. Differences in the catalytic mechanisms of mesophilic and thermophilic indole-3-glycerol phosphate synthase enzymes at their adaptive temperatures. Biochem. Biophys. Res. Commun. 2012, 418, 324–329. [Google Scholar] [CrossRef] [PubMed]
  25. Zaccardi, M.J.; Yezdimer, E.M.; Boehr, D.D. Functional identification of the general acid and base in the dehydration step of indole-3-glycerol phosphate synthase catalysis. J. Biol. Chem. 2013, 288, 26350–26356. [Google Scholar] [CrossRef] [PubMed]
  26. Bhabha, G.; Biel, J.T.; Fraser, J.S. Keep on moving: Discovering and perturbing the conformational dynamics of enzymes. Acc. Chem. Res. 2015, 48, 423–430. [Google Scholar] [CrossRef] [PubMed]
  27. Shen, H.B.; Xu, F.; Hu, H.R.; Wang, F.F.; Wu, Q.; Huang, Q.; Wang, H.H. Coevolving residues of (β/α)8-barrel proteins play roles in stabilizing active site architecture and coordinating protein dynamics. J. Struct. Biol. 2008, 164, 281–292. [Google Scholar] [CrossRef] [PubMed]
  28. Hennig, M.; Darimont, B.D.; Jansonius, J.N.; Kirschner, K. The catalytic mechanism of indole-3-glycerol phosphate synthase: Crystal structures of complexes of the enzyme from Sulfolobus solfataricus with substrate analogue, substrate, and product. J. Mol. Biol. 2002, 319, 757–766. [Google Scholar] [CrossRef]
  29. Zaccardi, M.J.; O’Rourke, K.F.; Yezdimer, E.M.; Loggia, L.J.; Woldt, S.; Boehr, D.D. Loop-loop interactions govern multiple steps in indole-3-glycerol phosphate synthase catalysis. Protein Sci. 2014, 23, 302–311. [Google Scholar] [CrossRef] [PubMed]
  30. Ferreiro, D.U.; Komives, E.A.; Wolynes, P.G. Frustration in biomolecules. Q. Rev. Biophys. 2014, 47, 285–363. [Google Scholar] [CrossRef] [PubMed]
  31. Rothschild, L.J.; Mancinelli, R.L. Life in extreme environments. Nature 2001, 409, 1092–1101. [Google Scholar] [CrossRef] [PubMed]
  32. Boehr, D.D.; Dyson, H.J.; Wright, P.E. An NMR perspective on enzyme dynamics. Chem. Rev. 2006, 106, 3055–3079. [Google Scholar] [CrossRef] [PubMed]
  33. Boehr, D.D.; McElheny, D.; Dyson, H.J.; Wright, P.E. The dynamic energy landscape of dihydrofolate reductase catalysis. Science 2006, 313, 1638–1642. [Google Scholar] [CrossRef] [PubMed]
  34. Carter, P.J.; Winter, G.; Wilkinson, A.J.; Fersht, A.R. The use of double mutants to detect structural changes in the active site of the tyrosyl-tRNA synthetase (bacillus stearothermophilus). Cell 1984, 38, 835–840. [Google Scholar] [CrossRef]
  35. Ghosh, A.; Sakaguchi, R.; Liu, C.; Vishveshwara, S.; Hou, Y.M. Allosteric communication in cysteinyl tRNA synthetase: A network of direct and indirect readout. J. Biol. Chem. 2011, 286, 37721–37731. [Google Scholar] [CrossRef] [PubMed]
  36. Nicholson, L.K.; Yamazaki, T.; Torchia, D.A.; Grzesiek, S.; Bax, A.; Stahl, S.J.; Kaufman, J.D.; Wingfield, P.T.; Lam, P.Y.; Jadhav, P.K.; et al. Flexibility and function in HIV-1 protease. Nat. Struct. Biol. 1995, 2, 274–280. [Google Scholar] [CrossRef] [PubMed]
  37. Zgiby, S.; Plater, A.R.; Bates, M.A.; Thomson, G.J.; Berry, A. A functional role for a flexible loop containing Glu182 in the class II fructose-1,6-bisphosphate aldolase from Escherichia coli. J. Mol. Biol. 2002, 315, 131–140. [Google Scholar] [CrossRef] [PubMed]
  38. Derewenda, Z.S. Structure and function of lipases. Adv. Protein Chem. 1994, 45, 1–52. [Google Scholar] [PubMed]
  39. Lebioda, L.; Stec, B.; Brewer, J.M. The structure of yeast enolase at 2.25-Å resolution. An 8-fold β + α-barrel with a novel β β α α (β α)6 topology. J. Biol. Chem. 1989, 264, 3685–3693. [Google Scholar] [PubMed]
  40. Lebioda, L.; Stec, B. Mechanism of enolase: The crystal structure of enolase-Mg2(+)-2-phosphoglycerate/phosphoenolpyruvate complex at 2.2-Å resolution. Biochemistry 1991, 30, 2817–2822. [Google Scholar] [CrossRef] [PubMed]
  41. Taylor, S.S.; Yang, J.; Wu, J.; Haste, N.M.; Radzio-Andzelm, E.; Anand, G. Pka: A portrait of protein kinase dynamics. Biochim. Biophys. Acta 2004, 1697, 259–269. [Google Scholar] [CrossRef] [PubMed]
  42. Kohen, A. Dihydrofolate reductase as a model for studies of enzyme dynamics and catalysis. F1000Res 2015, 4. [Google Scholar] [CrossRef] [PubMed]
  43. Gunasekaran, K.; Ma, B.; Nussinov, R. Triggering loops and enzyme function: Identification of loops that trigger and modulate movements. J. Mol. Biol. 2003, 332, 143–159. [Google Scholar] [CrossRef]
  44. Gunasekaran, K.; Nussinov, R. Modulating functional loop movements: The role of highly conserved residues in the correlated loop motions. Chembiochem 2004, 5, 224–230. [Google Scholar] [CrossRef] [PubMed]
  45. Sampson, N.S.; Knowles, J.R. Segmental motion in catalysis: Investigation of a hydrogen bond critical for loop closure in the reaction of triosephosphate isomerase. Biochemistry 1992, 31, 8488–8494. [Google Scholar] [CrossRef] [PubMed]
  46. Sampson, N.S.; Knowles, J.R. Segmental movement: Definition of the structural requirements for loop closure in catalysis by triosephosphate isomerase. Biochemistry 1992, 31, 8482–8487. [Google Scholar] [CrossRef] [PubMed]
  47. Berlow, R.B.; Igumenova, T.I.; Loria, J.P. Value of a hydrogen bond in triosephosphate isomerase loop motion. Biochemistry 2007, 46, 6001–6010. [Google Scholar] [CrossRef] [PubMed]
  48. Wang, Y.; Berlow, R.B.; Loria, J.P. Role of loop-loop interactions in coordinating motions and enzymatic function in triosephosphate isomerase. Biochemistry 2009, 48, 4548–4556. [Google Scholar] [CrossRef] [PubMed]
  49. Schnell, J.R.; Dyson, H.J.; Wright, P.E. Structure, dynamics, and catalytic function of dihydrofolate reductase. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 119–140. [Google Scholar] [CrossRef] [PubMed]
  50. Miller, G.P.; Wahnon, D.C.; Benkovic, S.J. Interloop contacts modulate ligand cycling during catalysis by Escherichia coli dihydrofolate reductase. Biochemistry 2001, 40, 867–875. [Google Scholar] [CrossRef] [PubMed]
  51. Miller, G.P.; Benkovic, S.J. Strength of an interloop hydrogen bond determines the kinetic pathway in catalysis by Escherichia coli dihydrofolate reductase. Biochemistry 1998, 37, 6336–6342. [Google Scholar] [CrossRef] [PubMed]
  52. Cameron, C.E.; Benkovic, S.J. Evidence for a functional role of the dynamics of glycine-121 of Escherichia coli dihydrofolate reductase obtained from kinetic analysis of a site-directed mutant. Biochemistry 1997, 36, 15792–15800. [Google Scholar] [CrossRef] [PubMed]
  53. Boehr, D.D.; Schnell, J.R.; McElheny, D.; Bae, S.H.; Duggan, B.M.; Benkovic, S.J.; Dyson, H.J.; Wright, P.E. A distal mutation perturbs dynamic amino acid networks in dihydrofolate reductase. Biochemistry 2013, 52, 4605–4619. [Google Scholar] [CrossRef] [PubMed]
  54. Bhabha, G.; Lee, J.; Ekiert, D.C.; Gam, J.; Wilson, I.A.; Dyson, H.J.; Benkovic, S.J.; Wright, P.E. A dynamic knockout reveals that conformational fluctuations influence the chemical step of enzyme catalysis. Science 2011, 332, 234–238. [Google Scholar] [CrossRef] [PubMed]
  55. Mauldin, R.V.; Sapienza, P.J.; Petit, C.M.; Lee, A.L. Structure and dynamics of the G121V dihydrofolate reductase mutant: Lessons from a transition-state inhibitor complex. PLoS ONE 2012, 7, e33252. [Google Scholar] [CrossRef] [PubMed]
  56. Vogeli, B.; Bibow, S.; Chi, C.N. Enzyme selectivity fine-tuned through dynamic control of a loop. Angew. Chem. Int. Ed. Engl. 2016, 55, 3096–3100. [Google Scholar] [CrossRef] [PubMed]
  57. Schneider, B.; Knochel, T.; Darimont, B.; Hennig, M.; Dietrich, S.; Babinger, K.; Kirschner, K.; Sterner, R. Role of the N-terminal extension of the (β/α)8-barrel enzyme indole-3-glycerol phosphate synthase for its fold, stability, and catalytic activity. Biochemistry 2005, 44, 16405–16412. [Google Scholar] [CrossRef] [PubMed]
  58. Loria, J.P.; Rance, M.; Palmer, A.G., 3rd. A TROSY CPMG sequence for characterizing chemical exchange in large proteins. J. Biomol. NMR 1999, 15, 151–155. [Google Scholar] [CrossRef] [PubMed]
  59. Axe, J.M.; Boehr, D.D. Long-range interactions in the alpha subunit of tryptophan synthase help to coordinate ligand binding, catalysis, and substrate channeling. J. Mol. Biol. 2013, 425, 1527–1545. [Google Scholar] [CrossRef] [PubMed]
Catalysts 06 00129 g001 1024
Figure 1. Competing β1α1 loop interactions are important for ssIGPS function. (a) Structure of the ssIGPS enzyme (PDB 1A53 [28]), showing the β1α1 loop in purple, catalytic residues Glu51 (blue), Lys53 (red) and Lys110 (orange), and residues modified in this manuscript to change the structure/dynamics of the β1α1 loop, including Arg64, Asp65 (both magenta) and Asn90 (green); (b) schematic highlighting the hydrogen bonding interactions of the β1α1 loop. On the C-terminal side of the loop, Arg64 and Asp65 engage in a hydrogen bonding network including residues on the α1 and α8’ helices. On the N-terminal side, Asn90 from the β2α2 loop can hydrogen bond with residues on the β1α1 loop, including Arg54. We propose that the β1α1 loop fluctuates between conformations favoring interactions on each side of the loop; (c) chemical mechanism of ssIGPS [25]. Lys110 initiates ring closure and decarboxylation by protonating the carbonyl oxygen. Glu51 and Lys53 act as the general base and acid, respectively, in the dehydration step. Importantly, Lys53 is on the β1α1 loop and Glu51 is on the β1 strand preceding the loop. Changes to the structural dynamics of the β1α1 loop would likely affect the chemical environments and positioning of these residues.
Figure 1. Competing β1α1 loop interactions are important for ssIGPS function. (a) Structure of the ssIGPS enzyme (PDB 1A53 [28]), showing the β1α1 loop in purple, catalytic residues Glu51 (blue), Lys53 (red) and Lys110 (orange), and residues modified in this manuscript to change the structure/dynamics of the β1α1 loop, including Arg64, Asp65 (both magenta) and Asn90 (green); (b) schematic highlighting the hydrogen bonding interactions of the β1α1 loop. On the C-terminal side of the loop, Arg64 and Asp65 engage in a hydrogen bonding network including residues on the α1 and α8’ helices. On the N-terminal side, Asn90 from the β2α2 loop can hydrogen bond with residues on the β1α1 loop, including Arg54. We propose that the β1α1 loop fluctuates between conformations favoring interactions on each side of the loop; (c) chemical mechanism of ssIGPS [25]. Lys110 initiates ring closure and decarboxylation by protonating the carbonyl oxygen. Glu51 and Lys53 act as the general base and acid, respectively, in the dehydration step. Importantly, Lys53 is on the β1α1 loop and Glu51 is on the β1 strand preceding the loop. Changes to the structural dynamics of the β1α1 loop would likely affect the chemical environments and positioning of these residues.
Catalysts 06 00129 g001
Catalysts 06 00129 g002 1024
Figure 2. Perturbing interactions of the β1α1 loop changes the identity of the rate-determining step of ssIGPS catalysis. (a) Solvent viscosity and isotope effects provide insight into the identity of the rate-determining step. Binding/release of substrate/product is dependent on solvent viscosity, but chemical steps are independent of solvent viscosity. Ring closure and decarboxylation are sensitive to D2O, owing to the protonation step involving Lys110; all other steps are largely insensitive to the presence of D2O; (b) The presence of solvent viscosity and isotope effects for variant and WT ssIGPS enzymes at 75 °C. Data for the WT enzyme and the N90A variant were taken from References [24] and [29], respectively.
Figure 2. Perturbing interactions of the β1α1 loop changes the identity of the rate-determining step of ssIGPS catalysis. (a) Solvent viscosity and isotope effects provide insight into the identity of the rate-determining step. Binding/release of substrate/product is dependent on solvent viscosity, but chemical steps are independent of solvent viscosity. Ring closure and decarboxylation are sensitive to D2O, owing to the protonation step involving Lys110; all other steps are largely insensitive to the presence of D2O; (b) The presence of solvent viscosity and isotope effects for variant and WT ssIGPS enzymes at 75 °C. Data for the WT enzyme and the N90A variant were taken from References [24] and [29], respectively.
Catalysts 06 00129 g002
Catalysts 06 00129 g003 1024
Figure 3. There are local, but not global, conformational changes induced by changing β1α1 loop interactions. (a) CD spectra for WT (black), R64A/D65A (magenta) and R64A/D65A/N90A (blue) ssIGPS enzymes; (b) 1H-15N HSQC comparing WT (black), N90A (green), R64A/D65A (magenta) and R64A/D65A/N90A (blue) variants. Resonances highlighted include those of the β1 strand (Ala47, Ile48, Ile49, Ala50, Glu51), the β1α1 loop (Lys53, Arg54, Lys55, Ser56, Ser58, Gly59) and the β2α2 loop (Phe89, Gly91 and Ser92). NMR data were collected at 310 K on samples containing ~1 mM protein in 25 mM potassium phosphate pH 7.0, 75 mM KCl, 1 mM EDTA, 1 mM DTT, 0.02% NaN3 and 10% (v/v) 2H2O.
Figure 3. There are local, but not global, conformational changes induced by changing β1α1 loop interactions. (a) CD spectra for WT (black), R64A/D65A (magenta) and R64A/D65A/N90A (blue) ssIGPS enzymes; (b) 1H-15N HSQC comparing WT (black), N90A (green), R64A/D65A (magenta) and R64A/D65A/N90A (blue) variants. Resonances highlighted include those of the β1 strand (Ala47, Ile48, Ile49, Ala50, Glu51), the β1α1 loop (Lys53, Arg54, Lys55, Ser56, Ser58, Gly59) and the β2α2 loop (Phe89, Gly91 and Ser92). NMR data were collected at 310 K on samples containing ~1 mM protein in 25 mM potassium phosphate pH 7.0, 75 mM KCl, 1 mM EDTA, 1 mM DTT, 0.02% NaN3 and 10% (v/v) 2H2O.
Catalysts 06 00129 g003
Catalysts 06 00129 g004 1024
Figure 4. Disrupting β1α1 loop interactions changes loop structural dynamics across multiple timescales. (a) Backbone positions on the β1α1 loop are color coded according to the Rex value, which reports on the contribution of conformational exchange to the NMR R2 relaxation rate. Blue, magenta and red colors report on Rex values of less than 3 s−1, between 3 and 5 s−1 and greater than 5 s−1, respectively. Positions in black indicate that there is no data for these residues; (b) backbone positions on the β1α1 loop are color coded according to the 1H-15N heteronuclear Overhauser effects (hetNOEs); smaller hetNOE values generally correspond to less backbone structural ordering on the ps-ns timescale. Blue, purple, magenta and red colors report on hetNOE values greater than 0.9, between 0.8 and 0.9, between 0.7 and 0.8 and less than 0.7, respectively. Positions in black indicate that there is no data for these residues. NMR data were collected at 310 K on samples containing ~1 mM protein in 25 mM potassium phosphate pH 7.0, 75 mM KCl, 1 mM EDTA, 1 mM DTT, 0.02% NaN3 and 10% (v/v) 2H2O.
Figure 4. Disrupting β1α1 loop interactions changes loop structural dynamics across multiple timescales. (a) Backbone positions on the β1α1 loop are color coded according to the Rex value, which reports on the contribution of conformational exchange to the NMR R2 relaxation rate. Blue, magenta and red colors report on Rex values of less than 3 s−1, between 3 and 5 s−1 and greater than 5 s−1, respectively. Positions in black indicate that there is no data for these residues; (b) backbone positions on the β1α1 loop are color coded according to the 1H-15N heteronuclear Overhauser effects (hetNOEs); smaller hetNOE values generally correspond to less backbone structural ordering on the ps-ns timescale. Blue, purple, magenta and red colors report on hetNOE values greater than 0.9, between 0.8 and 0.9, between 0.7 and 0.8 and less than 0.7, respectively. Positions in black indicate that there is no data for these residues. NMR data were collected at 310 K on samples containing ~1 mM protein in 25 mM potassium phosphate pH 7.0, 75 mM KCl, 1 mM EDTA, 1 mM DTT, 0.02% NaN3 and 10% (v/v) 2H2O.
Catalysts 06 00129 g004
Catalysts 06 00129 g005 1024
Figure 5. Catalytic efficiency free energy changes induced by disrupting β1α1 loop interactions at 37 °C (blue) and 75 °C (red). ΔΔG values were calculated according to: ΔΔG = −RT ((kcat/KM)variant/(kcat/KM)WT.
Figure 5. Catalytic efficiency free energy changes induced by disrupting β1α1 loop interactions at 37 °C (blue) and 75 °C (red). ΔΔG values were calculated according to: ΔΔG = −RT ((kcat/KM)variant/(kcat/KM)WT.
Catalysts 06 00129 g005
Table
Table 1. Steady-state kinetic parameters for β1α1 loop variants.
Table 1. Steady-state kinetic parameters for β1α1 loop variants.
Enzyme VariantTemp. (°C)kcat 1 (s−1)KM 1 (nM)kcat/KM (M−1·s−1 × 106)kcat,WT/kcat,var.(kcat/KM)WT/(kcat/KM)var.SVESDKIE2 kinact. (h−1)
WT371.021735.80--0.6 35.8 34.86
751.778919.9--~0 33.6 3
N90A 4370.17742.36.02.50.15.22.49
750.55797.03.22.8~01.6
R64A/D65A370.5353841.391.914.17~02.024.9
751.657702.141.079.300.11.0
R64A/D65A/N90A370.3754770.7862.727.37~01.025.5
750.9655981.611.8312.4~04.3
1 Standard errors in kcat and KM values are typically 5%–10% and 20%–40%, respectively; 2 kinact. were found by linearly fitting the relative rate of reaction versus the time of incubation at 90 °C, and had R2 values of at least 0.95; 3 SVE and SDKIE values for WT ssIGPS taken from reference [24]; 4 values for N90A ssIGPS taken from reference [29].

Share and Cite

MDPI and ACS Style

O’Rourke, K.F.; Jelowicki, A.M.; Boehr, D.D. Controlling Active Site Loop Dynamics in the (β/α)8 Barrel Enzyme Indole-3-Glycerol Phosphate Synthase. Catalysts 2016, 6, 129. https://doi.org/10.3390/catal6090129

AMA Style

O’Rourke KF, Jelowicki AM, Boehr DD. Controlling Active Site Loop Dynamics in the (β/α)8 Barrel Enzyme Indole-3-Glycerol Phosphate Synthase. Catalysts. 2016; 6(9):129. https://doi.org/10.3390/catal6090129

Chicago/Turabian Style

O’Rourke, Kathleen F., Aneta M. Jelowicki, and David D. Boehr. 2016. "Controlling Active Site Loop Dynamics in the (β/α)8 Barrel Enzyme Indole-3-Glycerol Phosphate Synthase" Catalysts 6, no. 9: 129. https://doi.org/10.3390/catal6090129

APA Style

O’Rourke, K. F., Jelowicki, A. M., & Boehr, D. D. (2016). Controlling Active Site Loop Dynamics in the (β/α)8 Barrel Enzyme Indole-3-Glycerol Phosphate Synthase. Catalysts, 6(9), 129. https://doi.org/10.3390/catal6090129

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop