Ultrasonic Monitoring of Biocatalysis in Solutions and Complex Dispersions
Abstract
:1. Introduction
2. Monitoring of Chemical Reactions with Ultrasonic Velocity
2.1. Detection Principles. Reactions Progress Curves
2.2. Reactions Involving the Same Type of Covalent Bonds in Multiple Reactants and Products
2.3. Degree of Polymerization and Molar Mass of Linear Polymers or Oligomers
2.4. Calibration for Ultrasonic Velocity
2.4.1. Method 1
2.4.2. Method 1 in Hydrolysis of Oligomers and Polymers
2.4.3. Method 2
2.4.4. Method 3
2.4.5. Method 4
3. Monitoring of Chemical Reactions with Ultrasonic Attenuation
4. Measuring Procedures
4.1. Procedure 1
4.2. Procedure 2
4.3. Procedure 3. Measurements in Flow
5. Add-On Capabilities
6. Examples of Ultrasonic Reaction Progress Curves
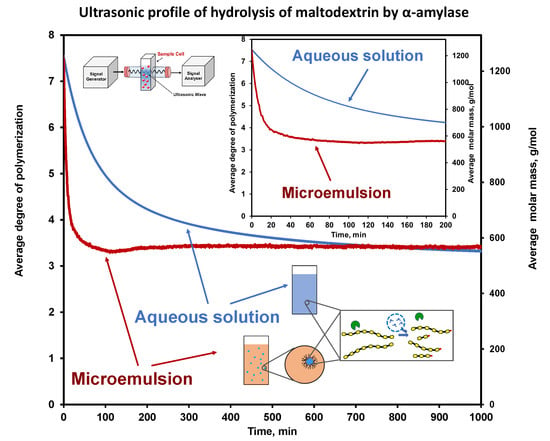
6.1. Hydrolysis of Maltodextrin
6.2. Hydrolysis of Lactose
6.3. Hydrolysis of Proteins
6.4. Synthesis of ATP
6.5. Decomposition of Hydrogen Peroxide Catalyzed by Metal Surfaces
6.6. Encapsulation of Substrates and Enzymes. Monitoring of Reactions in Nano-Droplets
6.6.1. Microemulsion Phase Diagrams. Optimal Conditions for Encapsulation of Enzymes and Reactants
6.6.2. HR-US Monitoring of Enzyme Catalyzed Reactions in Nanodroplets
7. Ultrasonic Reaction Rates and Advance Chemical Kinetics
8. Application of Extended Capabilities of Ultrasonic Spectroscopy
8.1. Dynamic Range
8.1.1. Ultrasonic Monitoring of Reverse Reactions
8.1.2. Assessment of Enzyme Deactivation during Long-Time Reactions
8.2. Titrations in Analysis of Effects of Enzyme Concentration
8.3. Temperature Profiling
9. Monitoring of Ultrasonic Attenuation
9.1. Structural Rearrangements and Particle Sizing
9.2. Fast Chemical Kinetics
10. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
Appendix A.1. Degree of Polymerization and Average Molar Mass
Appendix A.2. Relaxation Contribution to Ultrasonic Velocity and Attenuation
Appendix A.3. Ultrasonic Particle Sizing
Appendix A.4. Materials and Instruments Utilized in Previously Unpublished Illustrations
References
- Hall, A.M.; Chouler, J.C.; Codina, A.; Gierth, P.T.; Lowe, J.P.; Hintermair, U. Practical aspects of real-time reaction monitoring using multi-nuclear high resolution FlowNMR spectroscopy. Catal. Sci. Technol. 2016, 6, 8406–8417. [Google Scholar] [CrossRef]
- Kudryashov, E.; Smyth, C.; O'Driscoll, B.; Buckin, V. High-Resolution Ultrasonic Spectroscopy for analysis of chemical reactions in real time. Spectroscopy 2003, 18, 26–32. [Google Scholar]
- Danieli, E.; Perlo, J.; Duchateau, A.; Verzijl, G.; Litvinov, V.; Blümich, B.; Casanova, F. On-Line Monitoring of Chemical Reactions by using Bench-Top Nuclear Magnetic Resonance Spectroscopy. ChemPhysChem 2014, 15, 3060–3066. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, M.A.; Štefinović, M.; Sleigh, C.J. Optimising reaction performance in the pharmaceutical industry by monitoring with NMR. Magn. Reson. Chem. 2007, 45, 564–571. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Buckin, V. Ultrasonic real-time monitoring of the process of decomposition of hydrogen peroxide in aqueous solutions. Anal. Methods 2016, 8, 4828–4834. [Google Scholar] [CrossRef]
- Baltes, W. Rapid Methods for Analysis of Food and Food Raw Material; Behr‘s Verlag: Hamburg, Germany, 1990. [Google Scholar]
- Wiss, J.; Länzlinger, M.; Wermuth, M. Safety improvement of a Grignard reaction using on-line NIR monitoring. Org. Process Res. Dev. 2005, 9, 365–371. [Google Scholar] [CrossRef]
- Caras Altas, M.; Kudryashov, E.; Buckin, V. Ultrasonic monitoring of enzyme catalysis. Enzyme activity in formulations for lactose intolerant infants. Anal. Chem. 2016, 88, 4714–4723. [Google Scholar] [CrossRef] [PubMed]
- Wahler, D.; Reymond, J.-L. Novel methods for biocatalyst screening. Curr. Opin. Chem. Biol. 2001, 5, 152–158. [Google Scholar] [CrossRef]
- Bothner, B.; Chavez, R.; Wei, J.; Strupp, C.; Phung, Q.; Schneemann, A.; Siuzdak, G. Monitoring enzyme catalysis with mass spectrometry. J. Biol. Chem. 2000, 275, 13455–13459. [Google Scholar] [CrossRef] [PubMed]
- Mello, L.D.; Kubota, L.T. Review of the use of biosensors as analytical tools in the food and drink industries. Food Chem. 2002, 77, 237–256. [Google Scholar] [CrossRef]
- Povey, M.J.; Mason, T.J. Ultrasound in Food Processing; Springer: Berlin, Germany, 1998. [Google Scholar]
- Buckin, V. Application of High-Resolution Ultrasonic Spectroscopy for analysis of complex formulations. Compressibility of solutes and solute particles in liquid mixtures. IOP Conf. Ser. Mater. Sci. Eng. 2012, 42, 1–18. [Google Scholar] [CrossRef]
- Holmes, M.; Povey, M. Ultrasonic Particle Sizing in Emulsions. Ultrasound Food Proc. Recent Adv. 2017, 27–64. [Google Scholar] [CrossRef]
- Kaatze, U.; Eggers, F.; Lautscham, K. Ultrasonic velocity measurements in liquids with high resolution—Techniques, selected applications and perspectives. Meas. Sci. Technol. 2008, 19, 1–21. [Google Scholar] [CrossRef]
- Buckin, V.; Kudryashov, E.; O‘Driscoll, B. An alternative spectroscopy technique for biopharmaceutical applications. Pharm. Technol. Eur. 2002, 14, 33–37. [Google Scholar]
- Eigen, M.; De Maeyer, L. Techniques of Organic Chemistry; Friess, S.L., Lewis, E.S., Weisberger, A., Eds.; Investigation of Rates and Mechanisms of Reactions; Relaxation Methods Interscience: New York, NY, USA, 1963; Volume 8. [Google Scholar]
- Stuehr, J.; Yeager, E. Physical Acoustics; Mason, W.P., Ed.; Academic Press: New York, NY, USA, 1965; Volume 2. [Google Scholar]
- Smyth, C.; Kudryashov, E.; O‘Driscoll, B.; Buckin, V. High-resolution ultrasonic spectroscopy for analysis of industrial emulsions and suspensions. JALA J. Assoc. Lab. Autom. 2004, 9, 87–90. [Google Scholar] [CrossRef]
- Holmes, M.; Southworth, T.; Watson, N.; Povey, M. Enzyme Activity Determination Using Ultrasound; IOP Publishing: Bristol, UK, 2014; p. 012003. [Google Scholar]
- Resa, P.; Elvira, L.; De Espinosa, F.M.; Gómez-Ullate, Y. Ultrasonic velocity in water–ethanol–sucrose mixtures during alcoholic fermentation. Ultrasonics 2005, 43, 247–252. [Google Scholar] [CrossRef] [PubMed]
- Povey, M.J. Ultrasonic Techniques for Fluids Characterization; Academic Press Limited: London, UK, 1997. [Google Scholar]
- Buckin, V.; O’Driscoll, B. Ultrasonic waves and material analysis: Recent advances and future trends. LabPlus Int. 2002, 16, 17–21. [Google Scholar]
- Buckin, V.; Smyth, C. High-resolution ultrasonic resonator measurements for analysis of liquids. Semin. Food Anal. 1999, 4, 113–130. [Google Scholar]
- Resa, P.; Buckin, V. Ultrasonic analysis of kinetic mechanism of hydrolysis of cellobiose by beta-glucosidase. Anal. Biochem. 2011, 415, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Niemeyer, K. Ultrasonic Methods for Analytical Determination of Pancreatic Enzyme Activities in Pharmaceutical Preparations. Ph.D. Thesis, PHD Thesis Fakultät für Lebenswissenschaften der Technischen Universität Carolo-Wilhelmina, Braunschweig, Germany, 2012. [Google Scholar]
- Jager, M.; Kaatze, U.; Kudryashov, E.; O‘Driscoll, B.; Buckin, V. New capabilities of high-resolution ultrasonic spectroscopy: Titration analysis. Sperctoscopy 2005, 20, 20–26. [Google Scholar]
- Van Durme, K.; Delellio, L.; Kudryashov, E.; Buckin, V.; Van Mele, B. Exploration of high-resolution ultrasonic spectroscopy as an analytical tool to study demixing and remixing in poly(N-isopropyl acrylamide)/water solutions. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 1283–1295. [Google Scholar] [CrossRef]
- Hickey, S.; Lawrence, M.J.; Hagan, S.A.; Buckin, V. Analysis of the phase diagram and microstructural transitions in phospholipid microemulsion systems using high-resolution ultrasonic spectroscopy. Langmuir 2006, 22, 5575–5583. [Google Scholar] [CrossRef] [PubMed]
- Hickey, S.; Hagan, S.A.; Kudryashov, E.; Buckin, V. Analysis of phase diagram and microstructural transitions in an ethyl oleate/water/Tween 80/Span 20 microemulsion system using high-resolution ultrasonic spectroscopy. Int. J. Pharm. 2010, 388, 213–222. [Google Scholar] [CrossRef] [PubMed]
- Buckin, V.; Hallone, S.K. Ultrasonic Characterisation of W/O Microemulsions—Structure, Phase Diagrams, State of Water in Nano–Droplets, Encapsulated Proteins, Enzymes. In Microemulsions—An Introduction to Properties and Applications; InTech: London, UK, 2012; pp. 33–66. [Google Scholar]
- Bainor, A.; Chang, L.; McQuade, T.J.; Webb, B.; Gestwicki, J.E. Bicinchoninic acid (BCA) assay in low volume. Anal. Biochem. 2011, 410, 310–312. [Google Scholar] [CrossRef] [PubMed]
- Johnston, D.; Shoemaker, S.; Smith, G.; Whitaker, J. Kinetic measurements of cellulase activity on insoluble substrates using disodium 2, 2′ bicinchoninate. J. Food Biochem. 1998, 22, 301–319. [Google Scholar] [CrossRef]
- Adler-Nissen, J. Determination of the Degree of Hydrolysis of Food Protein Hydrolysates by Trinitrobenzenesulfonic Acid. J. Agric. Food Chem. 1979, 27, 1256–1262. [Google Scholar] [CrossRef] [PubMed]
- Kharakoz, D.P. Partial Volumes and Compressibilities of Extended Polypeptide Chains in Aqueous Solution: Additivity Scheme and Implication of Protein Unfolding at Normal and High Pressure. Biochemistry 1997, 36, 10276–10285. [Google Scholar] [CrossRef] [PubMed]
- Vorob’ev, M.; Levicheva, I.Y.; Belikov, V. Kinetics of the initial stage of milk protein hydrolysis by chymotrypsin. Appl. Biochem. Microbiol. 1996, 32, 219–222. [Google Scholar]
- Goncharova, I. Computer simulation of proteolysis. Peptic hydrolysis of partially demasked β-Lactoglobulin. Mol. Nutr. Food Res. 1998, 42, 61–67. [Google Scholar]
- Nihei, T.; Noda, L.; Morales, M.F. Kinetic Properties and Equilibrium Constant of the Adenosine Triphosphate-Creatine Transphosphorylase-catalyzed Reaction. J. Biol. Chem. 1961, 236, 3203–3209. [Google Scholar] [PubMed]
- Pierce, A.D. Acoustics: An Introduction to Its Physical Principles and Applications; American Institute of Physics: New York, NY, USA, 1989. [Google Scholar]
- Litovitz, T.A.; Davis, C.M. Physical Acoustics; Mason, W.P., Ed.; Academic Press: New York, NY, USA, 1964; Volume 2. [Google Scholar]
- Ochenduszko, A.; Buckin, V. Real-time monitoring of heat-induced aggregation of β-lactoglobulin in aqueous solutions using high-resolution ultrasonic spectroscopy. Int. J. Thermophys. 2010, 31, 113–130. [Google Scholar] [CrossRef]
- Hoshino, E.; Tanaka, A.; Kanda, T. Effects of a nonionic surfactant on the behavior of Bacillus amyloliquefaciens α-amylase in the hydrolysis of malto-oligosaccharide. J. Surfactants Deterg. 2006, 9, 63–68. [Google Scholar] [CrossRef]
- Robyt, J.; French, D. Action pattern and specificity of an amylase from Bacillus subtilis. Arch. Biochem. Biophys. 1963, 100, 451–467. [Google Scholar] [CrossRef]
- Yook, C.; Robyt, J.F. Reactions of alpha amylases with starch granules in aqueous suspension giving products in solution and in a minimum amount of water giving products inside the granule. Carbohydr. Res. 2002, 337, 1113–1117. [Google Scholar] [CrossRef]
- Rodriguez-Colinas, B.; Fernandez-Arrojo, L.; Ballesteros, A.; Plou, F. Galactooligosaccharides formation during enzymatic hydrolysis of lactose: Towards a prebiotic-enriched milk. Food Chem. 2014, 145, 388–394. [Google Scholar] [CrossRef] [PubMed]
- Jurado, E.; Camacho, F.; Luzon, G.; Vicaria, J.M. Kinetic models of activity for beta-galactosidases: Influence of pH, ionic concentration and temperature. Enzyme Microb. Technol. 2004, 34, 33–40. [Google Scholar] [CrossRef]
- Martínez-Villaluenga, C.; Cardelle-Cobas, A.; Corzo, N.; Olano, A.; Villamiel, M. Optimization of conditions for galactooligosaccharide synthesis during lactose hydrolysis by β-galactosidase from Kluyveromyces lactis (Lactozym 3000 L HP G). Food Chem. 2008, 107, 258–264. [Google Scholar] [CrossRef]
- Roefs, P.; de Kruif, K.G. Association behavior of native ß-lactoglobulin. Biopolymers 1999, 49, 11–20. [Google Scholar]
- Berg, J.M.; Tymoczko, T.J.; Stryer, L. Catalytic Strategies. In Biochemistry; WH Freeman and Company: New York, NY, USA, 2007; pp. 241–274. [Google Scholar]
- Lisak, K.; Toro-Sierra, J.; Kulozik, U.; Božanić, R.; Cheison, S.C. Chymotrypsin selectively digests β-lactoglobulin in whey protein isolate away from enzyme optimal conditions: Potential for native α-lactalbumin purification. J. Dairy Res. 2013, 80, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Maria, C.; Galvão, A.; Silva, A.F.S.; Custódio, M.F.; Monti, R.; De, R.; Giordano, C. Controlled hydrolysis of cheese whey proteins using trypsin and [alpha]-chymotrypsin. Appl. Biochem. Biotechnol. 2001, 91, 761–776. [Google Scholar]
- Brot, F.E.; Bender, M.L. Use of the specificity constant of. alpha.-chymotrypsin. J. Am. Chem. Soc. 1969, 91, 7187–7191. [Google Scholar] [CrossRef]
- Chae, H.J.; In, M.-J.; Kim, M.-H. Process development for the enzymatic hydrolysis of food protein: Effects of pre-treatment and post-treatments on degree of hydrolysis and other product characteristics. Biotechnol. Bioprocess Eng. 1998, 3, 35–39. [Google Scholar] [CrossRef]
- Clemente, A. Enzymatic protein hydrolysates in human nutrition. Trends Food Sci. Technol. 2000, 11, 254–262. [Google Scholar] [CrossRef]
- Korhonen, H. Milk-derived bioactive peptides: From science to applications. J. Funct. Foods 2009, 1, 177–187. [Google Scholar] [CrossRef]
- Dawson, D.M. Creatine kinase from brain: Kinetic aspects. J. Neurochem. 1970, 17, 65–74. [Google Scholar] [CrossRef] [PubMed]
- Tanzer, M.L.; Gilvarg, C. Creatine and Creatine Kinase Measurement. J. Biol. Chem. 1959, 234, 3201–3204. [Google Scholar] [PubMed]
- Lin, S.-S.; Gurol, M.D. Catalytic Decomposition of Hydrogen Peroxide on Iron Oxide: Kinetics, Mechanism, and Implications. Environ. Sci. Technol. 1998, 32, 1417–1423. [Google Scholar] [CrossRef]
- Watts, R.J.; Foget, M.K.; Kong, S.-H.; Teel, A.L. Hydrogen peroxide decomposition in model subsurface systems. J. Hazard. Mater. 1999, 69, 229–243. [Google Scholar] [CrossRef]
- Petri, B.G.; Watts, R.J.; Teel, A.L.; Huling, S.G.; Brown, R.A. Fundamentals of ISCO Using Hydrogen Peroxide. In In Situ Chemical Oxidation for Groundwater Remediation; Siegrist, R.L., Crimi, M., Simpkin, T.J., Eds.; Springer: New York, NY, USA, 2011; pp. 33–88. [Google Scholar]
- Zepp, R.G.; Faust, B.C.; Hoigne, J. Hydroxyl radical formation in aqueous reactions (pH 3–8) of iron(II) with hydrogen peroxide: The photo-Fenton reaction. Environ. Sci. Technol. 1992, 26, 313–319. [Google Scholar] [CrossRef]
- Kwan, W.P.; Voelker, B.M. Decomposition of Hydrogen Peroxide and Organic Compounds in the Presence of Dissolved Iron and Ferrihydrite. Environ. Sci. Technol. 2002, 36, 1467–1476. [Google Scholar] [CrossRef] [PubMed]
- Chu, L.; Wang, J.; Dong, J.; Liu, H.; Sun, X. Treatment of coking wastewater by an advanced Fenton oxidation process using iron powder and hydrogen peroxide. Chemosphere 2012, 86, 409–414. [Google Scholar] [CrossRef] [PubMed]
- Chakinala, A.G.; Bremner, D.H.; Gogate, P.R.; Namkung, K.-C.; Burgess, A.E. Multivariate analysis of phenol mineralisation by combined hydrodynamic cavitation and heterogeneous advanced Fenton processing. Appl. Catal. B Environ. 2008, 78, 11–18. [Google Scholar] [CrossRef]
- Doong, R.-A.; Chang, W.-H. Photodegradation of parathion in aqueous titanium dioxide and zero valent iron solutions in the presence of hydrogen peroxide. J. Photochem. Photobiol. A Chem. 1998, 116, 221–228. [Google Scholar] [CrossRef]
- Bremner, D.H.; Burgess, A.E.; Houllemare, D.; Namkung, K.-C. Phenol degradation using hydroxyl radicals generated from zero-valent iron and hydrogen peroxide. Appl. Catal. B Environ. 2006, 63, 15–19. [Google Scholar] [CrossRef]
- Kolisis, F.N.; Stamatis, H.; Flickinger, M.C. Reverse Micelles, Enzymes. In Encyclopedia of Industrial Biotechnology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Stamatis, H.; Xenakis, A.; Kolisis, F.N. Bioorganic reactions in microemulsions: The case of lipases. Biotechnol. Adv. 1999, 17, 293–318. [Google Scholar] [CrossRef]
- Smyth, C.; O’Driscoll, B.; Lawrence, J.; Hickey, S.; O’Reagan, T.; Buckin, V. High-Resolution Ultrasonic Spectroscopy Analysis of Microemulsions. Pharm. Technol. Eur. 2004, 16, 31–34. [Google Scholar]
- Tonova, K.; Lazarova, Z. Reversed micelle solvents as tools of enzyme purification and enzyme-catalyzed conversion. Biotechnol. Adv. 2008, 26, 516–532. [Google Scholar] [CrossRef] [PubMed]
- Maruhenda-Egea, F.C.; Piera-Vélasquez, S.; Cadenas, C.; Cadenas, E. Reverse micelles in organic solvents: A medium for the biotechnological use of extreme halophilic enzymes at low salt concentration. Archaea 2002, 1, 105–111. [Google Scholar] [CrossRef]
- Dorovska-Taran, V.; Veeger, C.; Visser, A.J.W.G. Reverse micelles as a water-property-control system to investigate the hydration/activity relationship of α-chymotrypsin. Eur. J. Biochem. 1993, 218, 1013–1019. [Google Scholar] [CrossRef] [PubMed]
- Panintrarux, C.; Adachi, S.; Araki, Y.; Kimura, Y.; Matsuno, R. Equilibrium yield of n-alkyl-β-d-glucoside through condensation of glucose and n-alcohol by β-glucosidase in a biphasic system. Enzyme Microb. Technol. 1995, 17, 32–40. [Google Scholar] [CrossRef]
- Kouptsova, O.S.; Klyachko, N.L.; Levashov, A.V. Synthesis of Alkyl Glycosides Catalyzed by β-Glycosidases in a System of Reverse Micelles. Russian J. Bioorganic Chem. 2001, 27, 380–384. [Google Scholar] [CrossRef]
- Grous, W.; Converse, A.; Grethlein, H.; Lynd, L. Kinetics of cellobiose hydrolysis using cellobiase composites from Ttrichoderma reesei and Aspergillus niger. Biotechnol. Bioeng. 1985, 27, 463–470. [Google Scholar] [CrossRef] [PubMed]
- Gong, C.-S.; Ladisch, M.R.; Tsao, G.T. Cellobiase from Trichoderma viride: Purification, properties, kinetics, and mechanism. Biotechnol. Bioeng. 1977, 19, 959–981. [Google Scholar] [CrossRef] [PubMed]
- Segel, I.H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Boy, M.; Dominik, A.; Voss, H. Fast determination of biocatalyst process stability. Process Biochem. 1999, 34, 535–547. [Google Scholar] [CrossRef]
- Neri, D.F.; Balcão, V.M.; Carneiro-da-Cunha, M.G.; Carvalho, L.B., Jr.; Teixeira, J.A. Immobilization of β-galactosidase from Kluyveromyces lactis onto a polysiloxane–polyvinyl alcohol magnetic (mPOS–PVA) composite for lactose hydrolysis. Catal. Commun. 2008, 9, 2334–2339. [Google Scholar] [CrossRef] [Green Version]
- Dwyer, C.; Donnelly, L.; Buckin, V. Ultrasonic analysis of rennet-induced pre-gelation and gelation processes in milk. J. Dairy Res. 2005, 72, 303–310. [Google Scholar] [CrossRef] [PubMed]
- Lehmann, L.; Buckin, V. Determination of the Heat Stability Profiles of Concentrated Milk and Milk Ingredients Using High Resolution Ultrasonic Spectroscopy. J. Dairy Sci. 2005, 88, 3121–3129. [Google Scholar] [CrossRef]
- Griffin, W.G.; Griffin, M.C.A. The attenuation of ultrasound in aqueous suspensions of casein micelles from bovine milk. J. Acoust. Soc. Am. 1990, 87, 2541–2550. [Google Scholar] [CrossRef]
- Holt, C.; Dalgleish, D.G. Electrophoretic and hydrodynamic properties of bovine casein micelles interpreted in terms of particles with an outer hairy layer. J. Colloid Interface Sci. 1986, 114, 513–524. [Google Scholar] [CrossRef]
- Adler-Nissen, J. Enzymic Hydrolysis of Food Proteins; Elsevier Applied Science Publishers Ltd.: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Jürgens, K.D.; Baumann, R. Ultrasonic absorption studies of protein-buffer interactions. Eur. Biophys. J. 1985, 12, 217–222. [Google Scholar] [CrossRef] [PubMed]
- Slutsky, L.; Madsen, L.; White, R. Acoustic absorption and proton-exchange kinetics in aqueous bovine pancreatic ribonuclease A. J. Phys. Chem. 1984, 88, 5679–5683. [Google Scholar] [CrossRef]
- Slutsky, L.; Madsen, L.; White, R.; Harkness, J. Kinetics of the exchange of protons between hydrogen phosphate ions and a histidyl residue. J. Phys. Chem. 1980, 84, 1325–1329. [Google Scholar] [CrossRef]
- Rogez, D.; Cerf, R.; Andrianjara, R.; Salehi, S.-T.; Fouladgar, H. Ultrasonic studies of proton-transfer reactions at the catalytic site of α-chymotrypsin. FEBS Lett. 1987, 219, 22–26. [Google Scholar] [CrossRef]
- Strom-Jensen, P.R.; Dunn, F. Ultrasonic absorption by solvent–solute interactions and proton transfer in aqueous solutions of peptides and small proteins. J. Acoust. Soc. Am. 1984, 75, 960–966. [Google Scholar] [CrossRef]
- Johnson, J.; Srisuthep, R. Physical and chemical properties of oligosaccharides. Cereal Chem. 1975, 52, 70–78. [Google Scholar]
- Chirife, J.; Buera, M. A simple model for predicting the viscosity of sugar and oligosaccharide solutions. J. Food Eng. 1997, 33, 221–226. [Google Scholar] [CrossRef]
- Avaltroni, F.; Bouquerand, P.; Normand, V. Maltodextrin molecular weight distribution influence on the glass transition temperature and viscosity in aqueous solutions. Carbohydr. Polym. 2004, 58, 323–334. [Google Scholar] [CrossRef]
- Dokic, P.; Jakovljevic, J.; Dokic-Baucal, L. Molecular characteristics of maltodextrins and rheological behaviour of diluted and concentrated solutions. Colloids Surf. A Physicochem. Eng. Asp. 1998, 141, 435–440. [Google Scholar] [CrossRef]
- Kaatze, U.; Hushcha, T.; Eggers, F. Ultrasonic Broadband Spectrometry of Liquids A Research Tool in Pure and Applied Chemistry and Chemical Physics. J. Solut. Chem. 2000, 29, 299–368. [Google Scholar] [CrossRef]
- Epstein, P.S.; Carhart, R.R. The absorption of sound in suspensions and emulsions. I. Water fog in air. J. Acoust. Soc. Am. 1953, 25, 553–565. [Google Scholar] [CrossRef]
- Waterman, P.C.; Truell, R. Multiple scattering of waves. J. Math. Phys. 1961, 2, 512–537. [Google Scholar] [CrossRef]
- Fikioris, J.; Waterman, P. Multiple Scattering of Waves. II. “Hole Corrections” in the Scalar Case. J. Math. Phys. 1964, 5, 1413–1420. [Google Scholar] [CrossRef]
- Lloyd, P.; Berry, M. Wave propagation through an assembly of spheres: IV. Relations between different multiple scattering theories. Proc. Phys. Soc. 1967, 91, 678. [Google Scholar] [CrossRef]
- Allegra, J.; Hawley, S. Attenuation of sound in suspensions and emulsions: Theory and experiments. J. Acoust. Soc. Am. 1972, 51, 1545–1564. [Google Scholar] [CrossRef]
- McClements, D.; Coupland, J. Theory of droplet size distribution measurements in emulsions using ultrasonic spectroscopy. Colloids Surf. A Physicochem. Eng. Asp. 1996, 117, 161–170. [Google Scholar] [CrossRef]
- McClements, D.J.; Hemar, Y.; Herrmann, N. Incorporation of thermal overlap effects into multiple scattering theory. J. Acoust. Soc. Am. 1999, 105, 915–918. [Google Scholar] [CrossRef]

















| Reaction | Method 1 | Method 2 | Method 3 | Conditions |
|---|---|---|---|---|
| Hydrolysis of lactose, Reactions (R2, R4) | ≅0.018119 −2.003388 × 10−4 T +1.47128 × 10−6 T2 | - | - | Infant milk, temperature, T, 10 to 50 °C a |
| Hydrolysis of lactose, Reactions (R2, R4) | 0.0144 ±0.0002 | 0.0136 ±0.0006 | - | Dilute aqueous solutions (0 to 0.2 kg/kg), 20 °C a |
| Synthesis of ATP, Reaction (R6) | - | −0.0306 ±0.0009 | −0.0310 ±0.0003 | Dilute aqueous solutions, of ADP, 15 mM of phosphocreatine in 50 mM gly-gly buffer, 0.02% BSA, 5 mM Mg acetate, 25 °C, pH 7.4 |
| Hydrolysis of maltodextrin, Reactions (R2, R3) | 0.0240 ±0.0002 | - | - | Dilute aqueous solutions (0.01 and 0.02 kg/kg), 25 °C |
| Hydrolysis of maltodextrin, Reactions (R2, R3) | −0.0093 ±0.0008 | - | - | IPM microemulsion, 25 °C, 0.025 kg/kg in aqueous phase |
| Hydrolysis of protein, β-lactoglobulin, by α-chymotrypsin, Reactions (R2, R5) | - | 0.0700 ±0.0015 | - | Dilute aqueous solutions (0 to 0.01 kg/kg), 25 °C, 0.1 mol/L potassium phosphate buffer, pH 7.8 |
| Decomposition of hydrogen peroxide, Reaction (R7) | ≅−5.74685 × 10−3 +1.61885 × 10−4 −1.0225 × 10−6 | - | - | Infinite dilution in water (for concentrated solutions see Figure 2B), temperature, , 20 to 50 °C |
| Hydrolysis of cellobiose, Reactions (R2, R8) | 0.0126 ±0.0002 | 0.013 ±0.001 | - | Dilute aqueous solutions (0 to 0.1 kg/kg), 50 °C b |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buckin, V.; Altas, M.C. Ultrasonic Monitoring of Biocatalysis in Solutions and Complex Dispersions. Catalysts 2017, 7, 336. https://doi.org/10.3390/catal7110336
Buckin V, Altas MC. Ultrasonic Monitoring of Biocatalysis in Solutions and Complex Dispersions. Catalysts. 2017; 7(11):336. https://doi.org/10.3390/catal7110336
Chicago/Turabian StyleBuckin, Vitaly, and Margarida Caras Altas. 2017. "Ultrasonic Monitoring of Biocatalysis in Solutions and Complex Dispersions" Catalysts 7, no. 11: 336. https://doi.org/10.3390/catal7110336
APA StyleBuckin, V., & Altas, M. C. (2017). Ultrasonic Monitoring of Biocatalysis in Solutions and Complex Dispersions. Catalysts, 7(11), 336. https://doi.org/10.3390/catal7110336