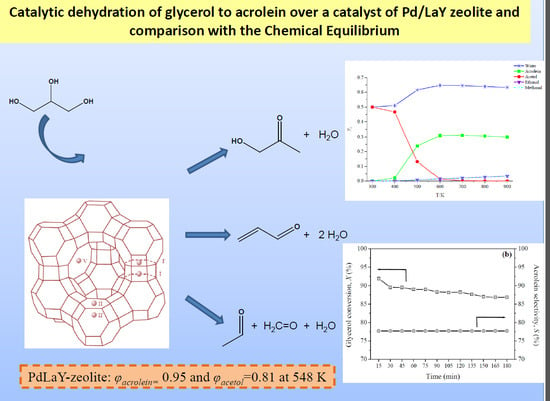
Catalytic Dehydration of Glycerol to Acrolein over a Catalyst of Pd/LaY Zeolite and Comparison with the Chemical Equilibrium

Abstract

Glycerol dehydration to acrolein was studied with three catalysts using zeolite-Y. This zeolite in its protonic form (HY), with La (LaY) and Pd with La (Pd/LaY), was characterized by X-ray diffraction (XRD), Fourier-transform-infrared spectroscopy (FTIR) with pyridine, BET, Scanning Electron Microscope (SEM)–Energy-Dispersive Spectroscopy X-ray (EDS) and the catalytic activity tests were carried out under H₂ atmosphere. It was found that La ions exchanged in the zeolite-Y resulted in the improvement of both glycerol conversion and yield to acrolein, also a relatively constant glycerol conversion was achieved up to three hours, due to the presence of Pd on the catalyst and H₂ in the feed. The comparison of the calculated and experimental yields obtained from the catalytic tests of the Pd/LaY catalyst indicates a greater activity for the reaction to acrolein than for the reaction to acetol. The calculated equilibrium yields of the dehydration reaction from glycerol to acrolein, acetol, ethanal, methanol, and water and the experimental yields of a Pd/LaY catalyst were compared. Thermodynamically, a complete conversion of glycerol can be achieved since the general system remains exothermic and promotes the path to acetol below 480 K. Above this temperature the system consumes energy and favors the production of acrolein, reaching its maximum concentration at 600 K.

1. Introduction

Due to the development of the biodiesel industry, global production of glycerine has considerably increased. Biodiesel is one of the options for the partial substitution of diesel derived from petroleum and has provided positive results in USA, Europe, and South America regarding its use as fuel in internal combustion engines. This biofuel is produced by the transesterification reaction of triglycerides derived from animal fats or vegetable oils in the presence of a catalyst and a short chain alcohol to form the respective mono-alkyl esters of fatty acids plus glycerol as a by-product [1].

Even though there have been significant advances in the development of low-cost heterogeneous catalysts and raw materials [2,3,4], as well as processes of separation and purification of reaction products [5,6,7,8,9,10,11] the main constraint for commercialization of biodiesel in developing countries is the cost of using pure raw materials. Otherwise, the reaction yield diminishes drastically, and the saponification side reaction may be enhanced resulting in further operating expenses due to additional purification steps [2,9].

Moreover, the crude glycerol from the biodiesel industry has reached very low prices such as 44 US$·ton⁻¹ in 2012 [12], so, for the industry the development of new uses for glycerol has become an important issue for financial and environmental aspects. Additionally, according to reports from the Organisation for Economic Co-operation and Development (OECD) together with the Food and Agriculture Organization of the United Nations (FAO) [13], it is expected that glycerol production from the biodiesel industry will increase from approximately 30 billion litres in 2014 to 39 billion litres in 2024, resulting in an excess of glycerol that exceeds the demand required by the chemical industry, having as a consequence a further decrease in the market price and making evident the need to develop processes for its conversion into higher value products.

Under this scenario, in recent years research has been carried out to develop valorization processes so that glycerol may pass from its current status as a by-product into a raw material for the synthesis of other compounds, for which several catalytic and biotechnological processes have been studied [14,15,16,17,18,19,20].

Notably, glycerol dehydration has caused expectation, and interest, since it may produce either acrolein or acetol as major products depending on the reaction conditions and the acid sites present on the catalyst surface. These can be either Brønsted or Lewis acid sites, offering a route to renewable production contrasting with the current processes of synthesis from petroleum derivatives [21,22]. Both compounds show remarkable chemical properties due to each one presenting two functional groups: a C–C double bond conjugated with a carbonyl group as aldehyde in the acrolein molecule while the acetol structure involves a hydroxyl group and a carbonyl moiety in the form of a ketone.

Acrolein has wide use as a reagent or intermediate in industry to produce a variety of compounds such as methionine by reaction with methyl mercaptan and hydrogen cyanide, acrylic acid by oxidation of the carbonyl group, and its derivatives such as polymers and esters; propanol, allyl alcohol, and propanal by means of selective hydrogenation. Acrolein acetals, alkoxy-propionaldehydes, and alkoxy methyl acroleins may be produced by reaction between acrolein and alcohols, a combined hydration-hydrogenation process may produce 1,3-propanediol, pyridine bases are synthesized by a condensation-cyclization reaction of acrolein with other carbonyl compounds and ammonia or amines, while they may also react with dienes in several Diels-Alder reactions to produce compounds of technological interest [23].

Meanwhile, acetol is used in the textile industry as a reducing agent for dyes instead of sodium dithionite avoiding sulfur salts in the wastewater; also it is often a customary food additive to confer odor and flavor to bread and milk products and in the cosmetic industry, it is an ingredient in skin tanning products. Furthermore, acetol can be used as a raw material to synthesize valuable chemicals such as acetone, propanal, and 1,2-propanediol [24].

Through computational chemistry calculations, some studies have been developed to clarify the reaction mechanisms and the intermediate species involved in the catalytic dehydration of glycerol. However, although the authors do report some information about the energetics of the process, the data refer either to transition states, to elementary steps, or performed at a single temperature, or for a single reaction pathway, thus all offering a deeper knowledge of parameters such as distances between atoms, bond lengths, and bond angles [25,26,27].

From an experimental approach, the process has been studied in the presence of several solid catalysts such as single and mixed oxides with diverse compositions [28,29,30,31,32,33,34], protonated zeolites or those promoted with transition metals or rare earths [35,36,37,38], or as well, heteropolyacids with the Keggin structure (denoted henceforth as HPAs) supported on niobia (Nb₂O₅), titania (TiO₂), silica (SiO₂), or alumina (Al₂O₃) [39,40,41,42,43,44,45,46,47] and yielding mainly acrolein and acetol plus small amounts of several by-products such as aldehydes, carboxylic acids, and/or alcohols in the range of C₁–C₃. However, due to their unique physicochemical properties such as high specific surface area, pore size, and Lewis and Brønsted acidity, zeolites remain attractive for their study as catalysts for biomass conversion reactions.

Specifically, the zeolite Y, with faujasite-like structure, may be a potential catalyst for the dehydration of glycerol at an industrial scale due to its three-dimensional pore system originated by supercages surrounded by 10 sodalite units that form spheres of approximately 1.3 nm in diameter. These sorption cavities have openings delimited by six sodalite units which form a 12-membered oxygen ring of 0.74 nm diameter. Each sodalite unit is connected with four other sodalite cages through hexagonal prisms, originating with the connection of each supercage with four other cavities. Additionally, the tunable Si/Al ratio (usually from 1.5 to 6) and its ion exchange capacity with di- and trivalent cations provide the chance of modifying the acidity distribution [48,49,50].

So, thermodynamics provides valuable information such as the calculation of heat released or absorbed by a reactive system, the effect of temperature on the progress of reactions and on the equilibrium composition, and thus, the maximum conversion and product yields [51,52]. This paper focuses on the effect of temperature on product distribution besides comparing the product yields with those obtained from the catalytic dehydration of glycerol in the presence of a zeolite Y, exchanged with La and impregnated with Pd.

2. The Main Reactions

Previous studies have inspected and proposed the reaction mechanisms involved in glycerol dehydration. Based on a complete basis set calculation method, Nimlos et al. [27], showed the dehydration reaction routes of neutral and protonated glycerol considering two reaction mechanisms; in the case of neutral glycerol through 1,2- and 1,3-dehydration; while for the protonated glycerol the mechanisms are hydride transfer, pericyclic dehydration, and substitution reactions. They found that the first step is the formation of 1,3-dihydroxypropene (1,3-DHP) or 2,3-dihydroxypropene (2,3-DHP) by removing a water molecule from the neutral glycerol through 1,2-dehydration. Through 1,3-dehydration it is feasible that glycerol fragmentation yields a vinyl alcohol, methanol, and water.

Subsequently, 1,3-DHP may produce acrolein after the elimination of a second water molecule. It is noteworthy that both dihydroxy propenes and vinyl alcohol may show a keto-enol tautomerism reaction which implies their transformation towards the keto-isomers: 3-hydroxypropanal (3-HP), acetol, and ethanal, respectively (Figure 1).

On the other hand, when considering the protonated glycerol, it was found that the most stable transition states result in protonated forms of acetol and 3-HP as a result of hydride transfer. The latter may dehydrate to protonated acrolein or may be fragmented to protonated vinyl alcohol and methanal, or also to protonated ethanal and methanal at the expense of protonated glycerol, formed by a substitution mechanism [27].

Independently, Kongpatpanich et al. [25], developed Density Functional Theory (DFT) calculations to study the structures and reaction mechanisms of glycerol dehydration over an H-ZSM-5 zeolite. The reaction pathways obtained from their calculations were essentially the same as those of Nimlos et al. [27] for neutral glycerol in the sense of the formation of 1,3-DHP and 2,3-DHP, although they consider in the model the adsorption and protonation of the glycerol molecule over an H-ZSM-5 cluster. The compound 1,3-DHP is subsequently isomerized to 3-HP and finally loses a second water molecule yielding acrolein. Meanwhile, acetol is produced by the keto-enol tautomerization of 2,3-DHP promoted by the protonation of glycerol at the oxygen atom of the secondary hydroxyl group in the zeolite.

Martinuzzi et al. (2014) [53], proposed the reaction mechanism of glycerol dehydration and the subsequent transformation of its products by conducting the reaction over a solid acid catalyst in a fixed bed reactor, taking into account process variables such as temperature, glycerol concentration, gas hourly space velocity (GHSV) and oxygen concentration using nitrogen as carrier gas while the reaction products were analyzed by gas chromatography.

The authors, did not find the presence of 1,3-DHP, but they found 3-HP concentrations in the order of 1% which is in agreement with the fact that keto-isomers are more stable than enol-isomers—the keto-enol tautomerization of 1,3-DHP to form 3-HP being feasible which may yield acrolein by a second dehydration or methanal and ethanal by a retro-aldol reaction. Acetol was also detected and confirmed as a product of direct glycerol dehydration.

Other by-products such as acetone, acetic acid, propionic acid, propanal, methanol, ethanol, allyl alcohol, or complex oxygenated molecules were found each one in the order of 1 × 10⁻¹ to 1 × 10⁻² vol % by means of side-reactions such as hydrogenation/dehydrogenation, dehydration, oxidation, condensation/cyclization, and rearrangement promoted by the catalyst and the oxidizing atmosphere. However, although oxygen was used in the reaction feed, the formation of acrolein and acetol may be considered as the predominant route.

From these results and taking into account a non-reactive atmosphere (N₂) in order to analyze the behavior of the main reactions (Figure 2), the glycerol dehydration system may be considered as a set of three simultaneous reactions presented in Figure 2 Equations (1)–(3), from which acrolein and acetol are the primary reaction products while methanal and ethanal may be present at minor concentrations.

3. Results and Discussion

3.1. Catalyst Characterization

3.1.1. Concentration by Atomic Absorption

The La concentration by atomic absorption was 5.3 at % for the LaY catalyst and 5.1 at % for the Pd/LaY catalyst. These values were slightly lower than those found by Energy-Dispersive X-ray Spectroscopy (EDS) analysis.

3.1.2. N₂ Physisorption

Figure 3 shows the isothermal adsorption and desorption for HY, LaY, and Pd/LaY catalysts and the respective pore parameters. The isotherms for the three materials suggest that the solids are microporous, where there are monolayer-multilayer adsorption and capillary condensation in the pores. The materials exhibit a type I isotherm with a plateau at high relative pressures, as a result of the microporous nature of the solids with limited mesoporosity. Besides, a type H4 hysteresis was observed, and since these zeolites displayed a type I isotherm, this hysteresis is also a sign of microporosity [54,55,56].

As indicated by the N₂ physisorption analysis, the HY zeolite exhibits larger surface area, around 972 m²·g⁻¹, while the treatment with La caused a decrease of this parameter to 815 m²·g⁻¹ and the impregnation of Pd led to a surface area of 783 m²·g⁻¹, with a slight decline in pore volume from 0.36 to 0.30 and 0.29 cm³·g⁻¹, respectively. However, the pore diameter did not change significantly being around 14.75 Å. This behavior in the BET area was similar to that observed in the La-exchanged HY zeolite (588 m²·g⁻¹) and the parent HY zeolite (511 m²·g⁻¹) [57].

3.1.3. X-ray Diffraction

X-ray diffraction (XRD) was used to identify the crystalline phases in the HY, LaY, and Pd/LaY catalysts. As shown in Figure 4a–c the diffraction patterns recorded for the materials present characteristic reflections corresponding to sodium aluminum silicate hydrate (Joint Committee on Powder Diffraction Standards (JCPDS) 00-043-0168). Nevertheless, a slight shift toward smaller diffraction angles was displayed in the case of the impregnated catalysts, suggesting an increase in the unit cell dimensions.

For the HY zeolite, the most intense reflection was found at 15.75° of the 2θ scale corresponding to the (331) plane, while a group of secondary more intense reflections was exhibited at 20.5°, 24°, and 27.3°. On the other hand, after the treatment with La and, with La and Pd, the solid showed the appearance of a reflection corresponding to the (222) plane at 12.4° and a decrease in intensity of some reflections, resulting in the diffraction peak at 24° being the most intense.

Consistent with the literature [48,58], the cations incorporated after the ion exchange procedure of the HY-zeolite may be situated in five different locations at the supercages, at the sodalite cages or, at the hexagonal prisms. Illustrated in Figure 5, the locations are labeled as site I, at the center of the double 6-rings; site I′, in the sodalite cage and contiguous to a hexagonal ring shared by the sodalite cage and a double 6-ring; site II, in the supercage adjacent to an unshared hexagonal face of a sodalite cage; site II′, in the sodalite cage, nearby to an unshared hexagonal face, and, site V, in close proximity to the center of the 12-ring apertures between supercages.

According to Du et al. [59], the ratio of the intensities of the reflections of the (311) and (222) planes of the zeolite crystals, K = I₍₃₁₁₎/I₍₂₂₂₎, is indicative of the rare-earth cations distribution in the supercage and the sodalite cages. A higher value of K points to a larger number of cations located in the sodalite cages, which is the case of the La and Pd/LaY catalysts with a value of K = 1.9.

Additionally, the ion exchanged zeolite exhibited the presence of lanthanum hydroxide (La(OH)₃) (JCPDS 36-1481) as the secondary crystalline phase and lanthanum oxide (La₂O₃) (JCPDS 00-022-0369) in a minor proportion. The occurrence of La compounds in the XRD pattern indicates that besides La³⁺ ions being exchanged to stabilize the negative framework charge, a certain amount of La is deposited at the surface of the zeolite matrix. This idea is supported by the decrease of the surface area and the pore size volume determined by N₂ physisorption. Although the catalyst contains Pd in a low amount, it was not identifiable in the XRD pattern.

From the integrated areas of the most intense reflections, the relative percentages of the crystalline phases were calculated. Furthermore, the corresponding crystallite sizes were estimated too, taking into account the Scherrer equation (L = 0.9·λ/β·cos θ, where L is the crystallite size, λ the X-ray wavelength, β the line broadening, and θ the Bragg angle [60]), regarding the (331) plane for the HY zeolite and, (533), (101), and (101) planes for the zeolite matrix, La(OH)₃ ,and La₂O₃ in the LaY and Pd/LaY catalysts.

The results presented in

Table 1. Average crystallite sizes and relative percentages of the crystalline phases of the HY zeolite, LaY and Pd/LaY catalysts.

Sample	Zeolite Y		La(OH)3		La2O3
	%	L(533) (nm)	%	L(101) (nm)	%	L(101) (nm)
HY	100	19.05	-	-	-	-
LaY	88.30	32.54	10.25	47.89	1.45	103.10
Pd/LaY	88.18	32.47	10.18	48.00	1.64	103.16

indicate that the zeolite matrix prevailed as the main crystalline phase and that La occurred as La(OH)₃ mainly, representing approximately 10.3% and 10.2% of the composition in the LaY and Pd/LaY zeolites, while La₂O₃ coexisted amounting to 1.45% and 1.6% of the solids. This phase distribution of the La compounds may be attributed to the fact that the calcination temperature reached in the preparation of the catalyst (723 K) was not enough to perform the decomposition from La(OH)₃ to La₂O₃, since this transformation was reported to occur after 853 K [61].

Otherwise, the average crystal size of the HY-zeolite was estimated to be 20.16 nm and 19.05 nm from the (331) and (533) planes, correspondingly. The comparison of the average crystal sizes of the zeolite phase in the HY catalyst and the impregnated solids revealed an increase of approximately 13 nm after the ion exchange process. This enlargement may be attributed to the larger ionic radius of the La³⁺ cation (1.15 Å) in comparison to the radii of the Na⁺ and Al³⁺ ions, 0.95 Å and 0.50 Å, respectively.

3.1.4. IR Spectroscopy with Adsorption of Pyridine (IR-Py)

The IR-Py spectra at different temperatures of the HY zeolite, LaY and Pd/LaY catalysts are shown in Figure 6a–c, respectively. For the three solids, pyridine adsorption resulted in the appearance of characteristic bands of pyridine coordinated with the Lewis acid sites at 1622 cm⁻¹ and 1441 cm⁻¹, the bands corresponding to the protonation of pyridine on the Brønsted acid sites at approximately 1541 cm⁻¹ and 1636 cm⁻¹, and the bands attributed to pyridine adsorbed on both Brønsted and Lewis acid sites at 1490 cm⁻¹ [62]. The Brønsted acid sites with bands at 1541 cm⁻¹ and 1636 cm⁻¹ have been proposed as the catalytic species for the dehydration of glycerol to acrolein [40,63].

The desorption of pyridine at different temperatures indicates that the Lewis acid sites domain in the solid at low temperatures (from room temperature to 473 K) diminishes considerably as the temperature rises. The population of Brønsted sites is maintained and disappears in a smaller proportion relative to Lewis sites. The Brønsted acid sites (1541 cm⁻¹) of the protonated zeolite, almost vanished at 673 K.

Figure 7a–c show the quantification of Lewis and Brønsted acidity of the three catalysts at different temperatures by integrating the area of the IR bands related to each type of acid site. As seen in Figure 7a, at low temperature the Lewis acidity predominated, whereas, after 448 K, the Brønsted sites prevailed (Figure 7b), although with decreasing concentration with increase of temperature. On the other hand, an enhancement in the total amount of acid sites is observed after the exchange with La cations, increasing around 1.5 and 2.1 times the concentration of Lewis and Brønsted sites in the LaY catalyst regarding the HY zeolite, at 573 K. A subsequent increase of the acidity occurred after the impregnation of the LaY solid with Pd, leading to concentrations 2.5 and 3.5 times higher than the acidity of HY zeolite.

The effect of promoting acidity after the impregnation with La could be explained by regarding the ion exchange occurring during the impregnation process. According to Tynjälä and Pakkanen [64], the ion exchange of zeolites can be understood as a process in which the cations (usually Na⁺ or H⁺) that neutralize the negative charge resulting from tetrahedral Al are replaced by mono-, di-, or trivalent cations. Depending on the ion-exchange conditions, a framework Al atom can eventually be substituted by another trivalent cation. Due to this isomorphic substitution, new acid sites may be created [64]. This observation was made in another study with a HY-zeolite [57] in which the ion exchange of La with the HY-zeolite increased the concentration of both Lewis and Brønsted acid sites with regard to the acid sites of the parent HY-zeolite.

In the LaY and Pd/LaY catalysts, the La³⁺ cations partially replaced the framework Na⁺ cations as was revealed by EDS analysis (Figure 10) in which the Na concentration decrease from 8.9 to 2 atom % after the exchange with La, moreover there was not a significant change in Al concentration. It has been reported that the hydrolysis of water of solvation of La³⁺ cations create new Brønsted acid sites according to the Equation (4) [65,66]. The incorporation of La³⁺ also produced an increase in the area of the bands at 1450 cm⁻¹ and 1622 cm⁻¹.

[La(H₂O)_n]³⁺ + H₂O → [LaOH(H₂O)_n-1]²⁺ + H₃O⁺

(4)

or

La³⁺ + H₂O → [LaOH]²⁺ + H⁺

(5)

In another way, the origin of the acidity of the Pd/LaY catalyst, after Pd incorporation is related to the presence of residual Cl⁻ ions. It is known that the acidity of the OH groups present on the silica-alumina surface can be enhanced by the proximity of Cl⁻ ions: the development of surface acidity on alumina or silica-alumina, in which the electronic asymmetry set up by the proximity of the Cl⁻ ions draws electrons from the O–H bond, increasing the acidity of the group [48].

3.1.5. Scanning Electron Microscopy (SEM) and Energy-Dispersive X-ray Spectroscopy (EDS)

For both samples (HY and Pd/LaY), SEM and EDS were performed by analyzing two regions on a set of agglomerates. The images of the analyzed areas and the corresponding EDS analysis are shown in Figure 8 and Figure 9. The images of the solids (Figure 8a,b) demonstrate that the particles are spherical agglomerates, and their distribution is not homogeneous. The addition of La decreased the number of particles of 0.5 μm, from 60% to 20%. These images were similar to those obtained by Oliveira et al. [63] and Gu et al. [67] in which the particles showed octahedral crystals and their crystals of HY exhibited irregular octahedral morphology with size ranging from 1 μm to 1.5 μm. The average particle size of the HY sample (0.76 μm) in Figure 8a is similar to the average particle size of the Pd/LaY catalyst (0.92 μm) in Figure 8b.

In the EDS analysis , the atom ratio of Si/Al of the HY zeolite was 3.5, and the presence of 8.9 at % of Na (Figure 9a) was also observed. The amount of Na was 60% of the original Na atoms. In the case of LaY and Pd/LaY samples (Figure 9b,c), the concentration of La (5.2 at % and 5.8 at %) was the third highest after Al (20.6 at %) in the zeolite matrix, and a decrease in the amount of Na (3.5 at % and 2 at %) was noticed. In the Pd/LaY catalyst the atomic ratio of Si/Al (3.46) did not change significantly, suggesting that there was not an isomorphic substitution of Al³⁺ by La³⁺ ions. EDS did not detect the impregnated Pd in the zeolite due to the low amount of the metal.

3.2. Catalytic Activity

The HY, LaY and Pd/LaY catalysts were active in the conversion of glycerol at temperatures between 473 K and 573 K (

Table 2. Glycerol conversion and selectivities to acrolein and acetol of the HY, LaY, and Pd/LaY catalysts at different temperatures. (10 wt % glycerol, 0.3 g of catalyst and gas hourly space velocity (GHSV) = 5933 h⁻¹)

T(K)	HY			LaY			Pd/LaY
	XGlyc	SAcro	SAcet	XGlyc	SAcro	SAcet	XGlyc	SAcro	SAcet
473	45.1	54.1	44.3	72.4	60.2	36.9	89.1	42.1	46.1
523	55.4	75.8	18.0	77	86.7	11.7	90.0	67.7	27.1
548	57.5	91.6	3.72	80.9	99.0	0.15	91.0	77.7	17.6
573	61.6	93.0	0.81	84.1	89.41	0.09	93.0	94.2	2.75

), increasing their conversions with temperature such as thermodynamic study predicts. The HY catalyst showed a conversion of 57.5% and selectivity of acrolein of 91.6% at 548 K, while the catalyst H-zeolite-β tested at the same experimental conditions and reported by Dalla et al. [38], showed a conversion of 98% and acrolein selectivity of 78%. These results generate a yield of acrolein of 52% with the catalyst of the present study and 76.4% in the work of Dalla et al. [38] This comparison shows that zeolite-β was more active than zeolite-Y at the initial stages of the reaction.

The introduction of La into the HY catalyst, increased the acrolein yield from 57% to 75% at 573 K. which may be attributed to the increase in the concentration of the Lewis and Brønsted acid sites. It is known that the predominant route depends mainly on the nature of the acid sites. The mechanism for the formation of acrolein over Brønsted acid sites has been previously suggested, as well as the reaction of acetol over Lewis acid sites [68].

The introduction of Pd is related more with the stability of the catalyst than with the initial conversion and selectivity. However, in our catalyst, an initial acrolein yield of 87.6% was observed at 573 K, which was the highest among the three catalysts. This increase is related most probably to the higher acidity of the Pd/LaY catalyst with regard to the other catalysts and with the reactivity of Pd in the H₂ atmosphere.

For the three catalysts, the acrolein selectivity increased with increase of temperature as well as the addition of La to the HY zeolite. The LaY catalyst reached the highest value at 548 K (Table 2).

On the other hand, the Pd/LaY catalyst showed the smaller selectivity of the three catalysts reaching 77.7% at the same temperature. The selectivity towards acrolein showed the following order: LaY > HY > Pd/LaY.

When the Pd/LaY catalyst was evaluated between 15 and 180 min of time on stream (Figure 10a), the conversion was almost constant (X_glycerol between 92% and 87%), while for the LaY catalyst, the glycerol conversion decreased around 10% after 30 min of reaction, until 51% up to 180 min. With respect to the HY catalyst, the conversion of glycerol slightly decreased up to 135 min, falling drastically to 32.9% at 180 min.

The presence of Pd on the surface of the Pd/LaY catalyst under H₂ atmosphere produced a lower deactivation than the catalysts HY and LaY, without Pd up to 180 min (Figure 10a). The hydrogenation activity of this metal was used in the presence of H₂ to hydrogenate aromatic compounds [57] and possible precursors of coke formed during the reaction of glycerol dehydration. Other works in the literature show that the addition of Pd in the presence of H₂ for this reaction enables the catalyst to not be deactivated for up to more than 50 h at 593 K [69].

Another study of this reaction in an H₂ atmosphere of a catalyst with 0.3–0.5 wt % Pd, Pt, and Ru supported on Cs_2.5H_0.5PW₁₂O₄₀ showed improvement of catalytic activity against deactivation. Among the noble metals, the following order in stability was found: Pd > Pt ~ Ru [68].

Regarding the acrolein selectivity, the following order was observed: LaY > HY > Pd/LaY (Figure 10b). From Figure 7a,b, the Brønsted/Lewis acid sites ratio (B/L) for each catalyst was estimated at the reaction temperature of 548 K, obtaining the following order: LaY catalyst, B/L = 3.50, HY catalyst, B/L = 3.25 and Pd/LaY catalyst, B/L = 3.01. As can be seen, only the B/L ratio resulted in a proportional relationship towards acrolein selectivity.

The positive effect of the combination Pd-H₂ on glycerol conversion was evidenced when the Pd/LaY catalyst was evaluated under H₂ and N₂ atmosphere as carrier gas (Figure 11). In the presence of H₂ this catalyst showed a glycerol conversion close to 90% while with the use of N₂ its activity decreased after 30 min of reaction.

3.3. The Chemical Equilibrium

According to Equation (16), the reaction enthalpy at a given temperature may be calculated from the reaction enthalpy at the standard state, the difference of heat capacities between products and reactants at constant pressure, and at the given temperature. Also, the change of Gibbs free energy and equilibrium constants of the reaction at different temperatures are obtained considering Equations (15) and (17). Thermodynamic analysis of the glycerol dehydration was made from the standard enthalpies of formation and the Gibbs free energies of the compounds involved at different temperatures.

The glycerol dehydration reactions to obtain acrolein (reaction 1), methanal and ethanal (reaction 3) are endothermic processes requiring respectively 28.8 kJ·mol⁻¹ and 56.8 kJ·mol⁻¹ at 298.15 K (

Table 3. Reaction Enthalpy and change of Gibbs free energy as a function of reaction temperature for each reaction.

T (K)	Reaction 1		Reaction 2		Reaction 3
	ΔHr (kJ·mol−1)	ΔGr (kJ·mol−1)	ΔHr (kJ·mol−1)	ΔGr (kJ·mol−1)	ΔHr (kJ·mol−1)	ΔGr (kJ·mol−1)
298.15	28.84	−47.38	−33.99	−72.85	56.77	−17.19
300	28.89	−47.85	−33.98	−73.09	56.79	−17.65
400	30.61	−73.69	−33.63	−86.18	56.86	−42.47
500	31.09	−99.61	−33.98	−99.16	55.73	−66.97
600	30.54	−125.21	−34.75	−111.90	54.01	−90.99
700	29.18	−150.28	−35.75	−124.37	52.00	−114.55
800	27.30	−174.79	−36.90	−136.59	49.90	−137.74
900	25.20	−198.86	−38.09	−148.62	47.96	−160.74

), while the production of acetol (reaction 2) is an exothermic reaction which releases 34 kJ·mol⁻¹ at the same temperature.

According to the results of the change of Gibbs free energy of the reaction at different temperatures, the three reactions involved in glycerol dehydration are thermodynamically feasible. Figure 12 shows the behavior of equilibrium constants regarding temperature, calculated from Equation (17).

The formation of acrolein and acetol showed the highest values for K_p with opposite trends: (1 × 10⁸–1 × 10¹¹) and (1 × 10¹²–1 × 10⁸) between 300 K and 900 K, respectively. Therefore, reaction 2 predominates from 300 K to 500 K. On the other hand, although glycerol dehydration through reaction 3 is also thermodynamically feasible it is not competitive at any temperature.

It is important to mention that in the literature only a few studies have reported data on the thermodynamics of the glycerol dehydration [45,70]. However, this information seems to be insufficient since both authors only took into account the reaction to produce acrolein from glycerol, disregarding the reactions forming acetol and ethanal, and did not perform estimations of the equilibrium concentrations of reactants and products.

Talebian et al. [45] realized calculations of equilibrium constants from the experimental concentrations of glycerol, acrolein, and water; and estimations of standard entropy, enthalpy, and Gibbs free energy change from the dependence of the equilibrium constant with temperature in the range from 553 K to 613 K. The trend of the equilibrium constants (from 1.98 × 10³ to 2.82 × 10³) seems to be in agreement with the trend obtained in this work; however, the values are seven orders smaller than the data estimated in the present study. This difference may be due to the fact that the system did not reach the chemical equilibrium since the glycerol conversions (between 80% and 85%) are smaller than the theoretical ones, resulting in concentrations of reactants and products that may lead to different values of the thermodynamic equilibrium constant [71].

As shown in

Table 4. Comparison of thermodynamic data in the gaseous and liquid phases of compounds involved in acrolein production from glycerol.

Compound	ΔH°f (kJ·mol−1)			ΔG°f (kJ·mol−1)
	(a)	(b)	(c)	(a)	(b)	(c)
Glycerol	−583	−577.9	−669.3 b	−449	−447	−478.3 b
Acrolein	−81	−65.4	−98.9 a	−56.2	−37.3	−104.3 a
Water	−242	−241.8	−285.8 c	−243	−228.6	−306.7 c

(a) [70]; (b) This work, (c) Value for liquid phase, ^a Data estimated considering the enthalpy of vaporization of acrolein reported in [73], ^b [74], ^c [75].

, in the study of Sabater [70], the values of the thermodynamic properties of formation of the involved compounds differ widely from the data used in this work and from the values of the same properties in the liquid phase even though the authors pointed out that at low temperatures the reactants and products remain as liquids. These differences in values resulted in substantial deviations of the values of heats of reaction, Gibbs free energies, and equilibrium constants with respect to the values obtained in this study, using the Joback method (

Table 5. Comparison of thermodynamic properties of reaction to produce acrolein from glycerol

T (K)	ΔHr (kJ·mol−1)		ΔGr (kJ·mol−1)		K
	(a)	(b)	(a)	(b)	(a)	(b)
298.15	18.1	28.84	−92.6	−47.38	1.64 × 1016	2.00 × 108
553.15	20.4	30.79	−163	−113.39	2.66 × 1015	5.41 × 1010
563.15	20.5	30.74	−166	−115.95	2.59 × 1015	5.94 × 1010
573.15	20.6	30.68	−169	−118.37	2.53 × 1015	6.49 × 1010
593.15	20.7	30.57	−175	−123.58	2.42 × 1015	7.57 × 1010

(a) [70], (b) This work.

). It is important to mention that Sabater’s calculations were performed using the Predict Plus 2000 program, but the author gave neither details about the database or the theoretical models used for the estimation of the properties, nor a statistical analysis of the deviations of the values of the properties of the pure compounds considered. Additionally, although the estimations realized in our work were performed for ideal gas state conditions, even at low temperatures (from 300–450 K) the equilibrium constants in the gas phase offer a good approximation of liquid phase reactive systems because the thermodynamic properties that markedly affect the value of the equilibrium constant, namely enthalpy and entropy of reaction, change slightly in the case of the change from gas to liquid phase [72].

An equation for each independent reaction having the equilibrium constant regarding the reaction coordinates (ε_j) can be constructed using Equations (19) and (22), therefore the resulting equations for the reactive system are:

$${\left(\frac{P}{P°}\right)}^{-2}{K}_1=\frac{{\mathsf{\epsilon }}_1{\left(2{\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+{\mathsf{\epsilon }}_3\right)}^2}{{\left(2{\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+2{\mathsf{\epsilon }}_3+1\right)}^2\left({\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+{\mathsf{\epsilon }}_3-1\right)}$$

(6)

$${\left(\frac{P}{P°}\right)}^{-1}{K}_2=\frac{{\mathsf{\epsilon }}_2\left(2{\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+{\mathsf{\epsilon }}_3\right)}{{\left(2{\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+2{\mathsf{\epsilon }}_3+1\right)}^2\left({\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+{\mathsf{\epsilon }}_3-1\right)}$$

(7)

$${\left(\frac{P}{P°}\right)}^{-2}{K}_3=\frac{{\mathsf{\epsilon }}_3^2\left(2{\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+{\mathsf{\epsilon }}_3\right)}{{\left(2{\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+2{\mathsf{\epsilon }}_3+1\right)}^2\left({\mathsf{\epsilon }}_1+{\mathsf{\epsilon }}_2+{\mathsf{\epsilon }}_3-1\right)}$$

(8)

The equilibrium compositions (y_i) at different temperatures were calculated from the reaction coordinates computed by resolving the simultaneous Equations (6)–(8) using the multivariable Newton-Rhapson method and taking into account Equation (19) to calculate y_i for each involved compound (Figure 13). The production of acetol prevails at mild temperatures, mainly from 300–480 K, attaining y_acetol = 0.50−0.47 as its highest concentration between 300 K and 400 K, while its molar fraction decreases approximately 97% from 400 K to 600 K. In contrast, the acrolein concentration increases in the same temperature range reaching its maximum and staying around at y_acrolein = 0.31 between 600 K and 800 K.

Meanwhile, below 500 K the degree of advancement estimated for reaction 3 is neglectable, it increases and remains in the order of 1 × 10⁻² between 500 K and 800 K, which results in low molar fractions of methanal and ethanal but reaches a maximum value of y_i = 0.034 for each product at 900 K.

On the other hand, as was expected, the molar fraction of water in the whole system shows a higher value than the rest of the compounds throughout the temperature range over y_water = 0.50 and increases to 0.64 simultaneously with the formation of acrolein. In this reaction two molecules of water are released per molecule of glycerol. The numerical values over the molar fraction curve of water indicate the heat of reaction (in kJ·mol⁻¹) of the overall system after an enthalpy balance, weighting the degree of advancement of each independent reaction.

3.4. Comparison of Experimental and Calculated Yields

The comparison of the activity of the catalysts in this work concerning the equilibrium calculations is presented in Figure 14 regarding experimental molar yields (Y_i) and the yields estimated at the equilibrium conditions of acrolein, acetol, and ethanal. Other by-products have also been reported in the literature but they were not taken into account here, as they are products of secondary reactions, such as dehydrogenation/hydrogenation, decarbonylation, oxidation, condensation, and/or decomposition of the primary reaction products, and their selectivities or yields usually vary from one study to another depending on the nature of the catalyst.

At this point, it is important to mention that the theoretical product yields and the experimental ones may not necessarily be equal. The former are the maximum possible yields at chemical equilibrium conditions, i.e., time = ∞ and a closed system; and the fixed-bed reactor employed in this work represents an open system at steady-state in which, the contact time of the reactant and the catalyst usually is short, and the equilibrium for the parallel reactions, may not be reached due to different reaction rates and mass transport phenomena [76,77]. However, the comparison of the experimental and theoretical product yields may be indicative of how close to the chemical equilibrium the reactive system is, and if the reaction is fast and not rate-limiting [71].

According to the results of the chemical equilibrium analysis (Section 3.3), it is possible to reach complete conversion of glycerol between 400 K and 900 K. As seen in Figure 14a, when raising the temperature from 473 K to 573 K, the catalysts of this study showed an increase in glycerol conversion. However, none reached the complete conversion established by the thermodynamics. These results were compared with those obtained by Dalla et al. [38] with an NH₄La-β catalyst, for which the reaction conditions and the glycerol conversion were very close to the ones of the present work. The incomplete glycerol conversion may be attributed to the short residence times of the reactant occurring inside the fixed-bed reactor.

According to the equilibrium calculations, the yields of acrolein at the temperatures of the reaction used in this work (473–573 K), would be between 46% and 81% (Figure 14b). At the same range of temperature, the acrolein yields of the HY, LaY, and Pd/LaY catalysts lay between 24.4%–57.3%, 43.6%–75.2%, and 37.5%–87.6%, respectively, satisfying the premise that the experimental yield is lower than the theoretical value.

On the other hand, the equilibrium yields of acetol decreased from 51% to 12% when the reaction temperature increased from 473 K to 573 K. The experimental yields attained with the catalysts developed in this study, followed the theoretical trend with Y_acetol maximum values of 20% for HY, 26.7% for LaY, and 41.1% for Pd/LaY catalysts at 473 K, being all lower than the thermodynamic limit (Figure 14c).

The experimental yields of ethanal of the HY and LaY catalysts were too small at low temperatures but they increased significantly with the increase of temperature, remaining below the theoretical values (Figure 14d). In contrast, the yields of the Pd/LaY zeolite were the closest to the equilibrium values. On the other hand, the values found in the literature showed a significant increase in the production of ethanal in the presence of NH₄La-β catalyst, reaching higher yields than the equilibrium, which was attributed to secondary fragmentation reactions of acetol [38].

4. Materials and Methods

4.1. Catalyst Preparation

A commercial NaY zeolite, ammonium nitrate (NH₄NO₃)_, lanthanum nitrate (La(NO₃)₃) and palladium chloride (PdCl₂) were purchased from Sigma-Aldrich (Toluca, Mex., México) (Si/Al = 3.5). To obtain the protonated form of the solid, 2 g of the sodium zeolite were exchanged by constant stirring at 343 K during 2 h with 20 mL of NH₄NO₃ solution at 0.5 M. After this procedure, the resulting precipitate was washed with distilled water and vacuum filtered. The recovered solid was dried in an oven at 373 K for 12 h. Subsequently, it was ground and calcined in a furnace at 723 K over 2 h in air to obtain the HY zeolite.

For the ion exchange with La, a solution of 0.05 M La(NO₃)₃ was stirred with the HY zeolite for 2 h at 343 K. The solid was recovered by filtering under vacuum, washed with distilled water, dried at 373 K during 12 h, ground and, calcined at 723 K for 2 h and named LaY.

The impregnation of Pd on the LaY zeolite was conducted in order to obtain 0.3 wt% Pd by constant stirring of the La zeolite in a solution of PdCl₂ for 2 h at room temperature. The precipitate was washed, filtered, and dried in an oven for 12 h at 373 K, ground, and calcined at 723 K for 2 h. This solid was reduced in a H₂ flow of 2 L/h at 723 K for 2 h to obtain the Pd/LaY catalyst.

4.2. Catalyst Characterization

The concentration of La was evaluated by atomic absorption spectroscopy using a Perkin Elmer AAnalyst 400 instrument (Perkin Elmer de México, México, México). The samples were dissolved with a mixture of perchloric and nitric acids. The catalysts were subjected to N₂ physisorption analysis to determine their textural properties. Measurements of N₂ adsorption-desorption isotherms at 77 K were carried out in an ASAP-2450 (Micromeritics) equipment (Nanometrix, Naucalpan, Mex. México). The samples were previously outgassed at 573 K over 3 h under a vacuum of 1 × 10⁻³ Torr. During the determination of the adsorption isotherm, successive charges of gas (N₂) increasing the pressure were introduced into a vessel containing the sample, leaving sufficient time (15 s) to achieve balance at each point, thereby obtaining one adsorption isotherm characteristic of each solid.

The specific surface area values were obtained by application of the BET equation. The pore volume of the samples was calculated using the t-plot method. The calculation of the pore size was carried out by applying the BJH model to the desorption branch of the isotherm, assuming cylindrical pore geometry.

The solids were characterized by X-ray diffraction (XRD) to determine the type of structure and crystalline phases. The XRD patterns of the samples calcined at 723 K were obtained in a Bruker AXS diffractometer model D8 (Bruker Mexicana S.A, México, México) using CuKα radiation (1.5406 Å). The XRD patterns at higher angles (2θ ~ 10°–43°) were taken with a step size of 0.02° and a counting time of 2 s. The identification of the different crystalline phases was performed by comparison with the corresponding JCPDS diffraction data cards.

The surface acidity of the samples was measured by infrared spectroscopy of pyridine previously adsorbed, using an infrared spectroscope FTIR (Nicolet Model 170-SX) (Thermo Fisher Scientific Inc., México, México) allowing to determine the type and amount of surface acid sites. Each sample in pressed powder was put in a special glass cell in which the specimen temperature and the vacuum could be controlled. Pretreatment of the samples before the adsorption of pyridine consisted of degassing (1 × 10⁻³ Torr) followed by heating to 573 K at 20 K/min and cooling to room temperature. The sample was heated under vacuum with the intention of eliminating adsorbed water and surface impurities. After the pretreatment, the samples were exposed to a mixture of pyridine (4%) under N₂ over 15 min. for the chemisorption process at 298 K. The pyridine physically adsorbed was removed by vacuum and the infrared spectra were obtained in situ at temperatures from 298–373 K, 473 K, 573 K, and 673 K. The Lewis and Brønsted acid sites were identified according to the characteristic bands of the interaction of pyridine and each acid site [62]. The interaction of pyridine with the Brønsted acid sites led to the appearance of characteristic infrared bands at 1540 cm⁻¹ and 1640 cm⁻¹, while the Lewis sites exhibit bands at 1450 cm⁻¹, 1580 cm⁻¹, and 1600 cm⁻¹, and the contribution of both types of acid sites developed a band at 1490 cm⁻¹. The quantification of Brønsted and Lewis acid sites was performed regarding the integrated area of the bands at 1540 cm⁻¹ and 1450 cm⁻¹ respectively.

The observations of the catalysts in the electron microscope and imaging were performed in a high-resolution Scanning Electron Microscope (SEM) Field Emission JFM 6701 model F (Jeol de México S.A, México, México), brand Jeol, using secondary electrons. Qualitative chemical analysis and the corresponding spectra, and quantitative chemical analyses were obtained by coupling a probe SEM with energy-dispersive Spectroscopy X-ray (EDS) (Jeol de México S.A, México, México). For the observation, the catalyst powder was spread on a graphite tape and to make it conductive the necessary condition for obtaining images, Au atoms, were deposited.

4.3. Catalytic Activity

The glycerol dehydration reactions were performed at atmospheric pressure and controlled temperature in a microsystem comprised of mainly two consecutive saturation vessels and a fixed-bed reactor. From the first saturator, water vapor was carried with a H₂ flow at 60 mL·min⁻¹ and then bubbled into glycerol contained in the second saturator. To produce a gaseous mixture with 10 wt % of glycerol, the vapor pressure of water was 0.703 bar at 363 K, and the vapor pressure of glycerol was 0.021 bar at 451 K. The molar fractions of H₂:H₂O:glycerol were 0.087:0.894:0.019.

An amount of 0.3 g of catalyst was loaded into the reactor over a porous bed of fiberglass and reduced with a hydrogen flow of 60 mL·min⁻¹ over 2 h with heating at 723 K with an electrical furnace. Afterwards, the microreactor was allowed to reach the required reaction temperature (473 K, 523 K, 548 K, or 573 K) and then fed with the mixture previously described. According to the feeding conditions the GHSV was 5933 h⁻¹.

To recover independently the unreacted glycerol and the reaction products, the output stream from the reactor passed through a series of three collection traps at 326 K, 273 K, and 273 K, respectively. The glycerol concentration at the input and output of the reactor was monitored by measuring the refractive index with the use of a calibration curve of glycerol-water mixtures from 0–100 wt % of glycerol (Appendix B) with an Abbe refractometer Atago 1211. Additionally, the calibration curve of the refractive index of the glycerol-water mixtures was validated with the spectrophotometric method reported by Bondioli et al. [78], which uses glycerol oxidation with sodium periodate in the presence of acetylacetone using a wavelength of 410 nm. The reaction products were analyzed in a Varian 3400 gas chromatograph (Agilent Technologies México, México, México) equipped with a DB-WAX capillary column (30 m × 0.25 mm × 0.25 μm) and a flame ionization detector (FID). The glycerol conversion (X), product selectivity (S_i) and the experimental product yield (Y_i,Exp) were calculated by the following equations:

$$X (\%)=\frac{Moles of glycerol reacted}{Moles of glycerol fed}\times 100$$

(9)

$$S_i (\%)=\frac{Moles of product i}{Moles of glycerol reacted}\times 100$$

(10)

$$Y_{i, Exp}(\%)=\frac{X\times S_i}{100}$$

(11)

4.4. The Chemical Equilibrium

From the thermodynamic analysis in a reactive system, the effect of the reaction conditions, mainly temperature, on the resulting composition when approaching an equilibrium state can be determined. In this section a model is presented that relates the reactions involved in the system and the chemical composition at equilibrium conditions.

A chemical reaction may be expressed such as in Equation (12), where ν_i and ν_j are the stoichiometric coefficients of the i-th reactant A and j-th product B [79], respectively,

$${\displaystyle \sum _1^i}{\mathsf{\nu }}_i{A}_i\leftrightarrows {\displaystyle \sum _1^j}{\mathsf{\nu }}_j{B}_j$$

(12)

The change of Gibbs free energy of the reactive system diminishes continuously, expressing that change as:

$$\Delta G{°}_r={\displaystyle \sum _1^j}{\mathsf{\nu }}_j\Delta G{°}_{f,B_j}-{\displaystyle \sum _1^i}{\mathsf{\nu }}_i\Delta G{°}_{f,A_i}$$

(13)

where ΔG°_f,Ai and ΔG°_f,Bj are the change of Gibbs free energies of formation of reactants A and products B, which are reported in the literature or may be estimated by an adequate group contribution method (see Appendix A). When the change of free energy has attained the lowest value, the reaction rate approaches zero and the system is considered to have reached equilibrium. In this way, it is possible to express a constant employing the ratio of concentrations of products and reactants, or regarding the partial pressures in the case of gas phases, K_P,

$$K_P=\left(\frac{C_{P1}^{p1}{C}_{P2}^{p2}\dots C_{Pj}^{pj}}{C_{R1}^{r1}{C}_{R2}^{r2}\dots C_{Ri}^{ri}}\right)\left(\frac{P°}{P}\right)$$

(14)

On the other hand, at chemical equilibrium conditions, the change of Gibbs free energy of a reactive system may be expressed by:

$$\Delta G{°}_r=-RT\ln K$$

(15)

where R is the ideal gas constant, T is the reaction temperature, and K is the equilibrium constant which expresses the side of the reaction most favored: products if K > 1 or reactants if K < 1 [79,80] respectively. When Equation (15) is solved for lnK and is derived for T considering the definition of the Gibbs function, it is obtained:

$${\left(\frac{\partial \ln K}{\partial T}\right)}_p=\frac{\Delta H{°}_r}{R{T}^2}$$

(16)

Equation (16) is known as the Van’t Hoff equation and expresses the change of the equilibrium constant with temperature regarding the enthalpy of reaction, ΔH_r. If it is integrated between T = 298.15 and a second temperature T, it is written as:

$$\ln \frac{K_p\left(T\right)}{K_p\left(298.15\right)}={\displaystyle {\int }_{298.15}^T}\frac{\Delta H_r\left(T\right)}{R{T}^2} dT$$

(17)

which requires knowing the change of the enthalpy reaction with temperature, ΔH_r(T), which may be found from the following expression, where ΔC°_p is the difference of heat capacities at a constant pressure between products and reactants:

$$\Delta H_r\left(T\right)=\Delta H_r\left(298.15\right)+{\displaystyle {\int }_{298.15}^T}\Delta C{°}_p dT$$

(18)

In this way, if Equations (15), (17), and (18) are related, it is possible to develop a thermodynamic analysis of a reactive system regarding the change of enthalpies, change of Gibbs free energies, and equilibrium constants at different temperatures [51].

Furthermore, considering the reaction coordinate or degree of advancement (ε) such as the extension at which a reaction has occurred, for independent reactions the molar fraction of determined species in the reactive system is given by:

$$y_i=\frac{n_{i0}+{\sum }_j{\mathsf{\nu }}_{i,j}{\mathsf{\epsilon }}_j}{n_0+{\sum }_j{\mathsf{\nu }}_j{\mathsf{\epsilon }}_j}$$

(19)

where n_i0 is the moles of the i-th compound at the beginning of the reaction, n₀ represents the total initial moles, ν_i,j is the stoichiometric number of species i in the reaction j, ν_j is the sum of the stoichiometric coefficients of products and reactants involved in reaction j and ε_j is the advance of the j-th reaction [51,80].

So, for a multiple-reaction system,

$$\prod _i{\left(\frac{f_i}{f{°}_i}\right)}^{{\mathsf{v}}_{i,j}}=K_j$$

(20)

where f_i and f°_i are the fugacities of the compound in the mixture and at standard state, respectively, with

$$K_j=exp\left(\frac{-\Delta G{°}_j}{RT}\right)$$

(21)

If the equilibrium mixture is an ideal gas mixture (P° = 1 atm), then Equation (18) becomes:

$$\prod _i{\left(y_i\right)}^{{\mathsf{\nu }}_{i,j}}={\left(\frac{P}{P°}\right)}^{-{\mathsf{\nu }}_j}{K}_j$$

(22)

So, for r independent reactions there are r characteristic equations of this type and y_i may be eliminated considering Equations (19) and (22) for the r reaction coordinates ε_j [51].

Because the equations generated from the equilibrium relations and stoichiometry lead to a system of simultaneous nonlinear algebraic equations, considering r reaction coordinates ε_j as independent variables of the system, the Newton-Raphson method may be used to solve them simultaneously.

Usually, the catalytic activity is referred to as the reactant conversion or product selectivity. However, some catalysts reach maximum conversions, but low selectivities or in some cases the maximum selectivity does not imply a high conversion. For a system with parallel reactions sometimes it is useful to analyze the performance of a catalyst regarding the molar yield (Y_i) of a specific compound that involves the reactant conversion and the product selectivity. In order to realize screening of the activity of the catalysts reported in this work, the molar yields of acrolein and acetol obtained at the initial stages of the catalytic dehydration of glycerol were compared with the calculated yields from the chemical equilibrium calculations.

5. Conclusions

The LaY and Pd/LaY catalysts were more active in the conversion of glycerol than the HY zeolite reaching values of 73% and 90%, respectively. The conversion of glycerol increased with the increase of temperature as well as the acid sites concentration. The initial acrolein yields for the HY, LaY, and Pd/LaY catalysts at 573 K, were 57.3%, 75.2%, and 87.2% respectively. In the Pd/LaY catalyst, the presence of small amounts of Pd on the surface of the catalyst positively promoted the elimination of coke precursors as a result of reduction reactions in the presence of H₂.

Additionally, the calculation of thermodynamic data was performed considering the effect of temperature on the reactive system for which acetol and acrolein are the main products; while ethanal and methanal originated from fragmentation of glycerol, at high temperatures.

Taking into account the reaction enthalpies and the degree of advancement of each independent reaction at different temperatures, the heat of reaction of the overall system indicates that glycerol dehydration remains exothermic below 480 K, while the process consumes energy above this temperature.

From the estimated equilibrium compositions, the maximum yields for acetol and acrolein are around 0.95 and 0.88 at 400 K and 600 K, correspondingly.

The comparison of the calculated and experimental yields obtained from the catalytic tests of the LaY and Pd/LaY catalysts indicates greater activity for the reaction to acrolein than for the reaction to acetol, after the La exchange. The conversion of glycerol as a function of temperature followed the order: Pd/LaY > LaY > HY and the first catalyst showed the lowest difference with the equilibrium conversion.