A Three-Dimensional Numerical Assessment of Heterogeneity Impact on a Solid Oxide Fuel Cell’s Anode Performance
Abstract
:1. Introduction
2. Microstructure Data
3. Mathematical Model
4. Analytical Solution
5. Microstructure Modification
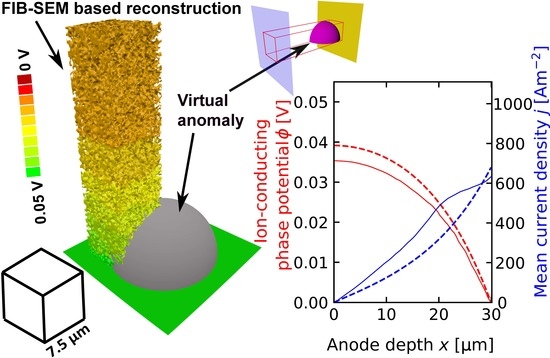
6. Results and Discussion
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | ||
| FIB | Focused Ion Beam | |
| SEM | Scanning Electron Microscopy | |
| SOFC | Solid Oxide Fuel Cell | |
| SOR | Successive Over-Relaxation | |
| TPB | Triple Phase Boundary | |
| YSZ | Yttrium-Stabilized Zirconia | |
| Roman symbols | ||
| d | Pore diameter | m |
| Diffusion coefficient | ||
| F | Faraday constant | |
| i | Charge transfer rate | |
| Equilibrium exchange current | ||
| j | Mean charge transfer rate | |
| TPB density | ||
| M | Molar mass | |
| p | Absolute pressure | Pa |
| Partial pressure of i | Pa | |
| h | Sphere-electrolyte distance | m |
| r | Sphere radius | m |
| R | Universal gas constant | |
| T | Temperature | K |
| v | Fuller-Schettler-Giddings correlation constant | - |
| V | Phase volume fraction | - |
| x,y | Planar coordinates | m |
| z | Depth | m |
| Greek symbols | ||
| Charge transfer coefficient | - | |
| Dimensionless constant | - | |
| Local overpotential | V | |
| Electrical potential | V | |
| Electrical conductivity | ||
| Tortuosity | - | |
| Subscripts | ||
| act | Activation | |
| an | Analytical | |
| b | Boundary (bulk) | |
| conc | Concentration | |
| eff | Effective, homogeneous model value | |
| Hydrogen | ||
| Water vapor | ||
| i | A substance | |
| ion | Oxide ion conducting phase | |
| tpb | Triple phase boundary | |
| 0 | Equilibrium | |
References
- Molenda, J.; Kupecki, J.; Baron, R.; Blesznowski, M.; Brus, G.; Brylewski, T.; Bucko, M.; Chmielowiec, J.; Cwieka, K.; Gazda, M.; et al. Status report on high temperature fuel cells in Poland—Recent advances and achievements. Int. J. Hydrogen Energy 2017, 42, 4366–4403. [Google Scholar] [CrossRef]
- Pieta, I.S.; Epling, W.S.; Kazmierczuk, A.; Lisowski, P.; Nowakowski, R.; Serwicka, E.M. Waste into Fuel—Catalyst and Process Development for MSW Valorisation. Catalysts 2018, 8, 113. [Google Scholar] [CrossRef]
- Brus, G.; Iwai, H.; Mozdzierz, M.; Komatsu, Y.; Saito, M.; Yoshida, H.; Szmyd, J.S. Combining structural, electrochemical, and numerical studies to investigate the relation between microstructure and the stack performance. J. Appl. Electrochem. 2017, 47, 979–989. [Google Scholar] [CrossRef]
- Onaka, H.; Iwai, H.; Kishimoto, M.; Saito, M.; Yoshida, H.; Brus, G.; Szmyd, J.S. Development of a charge-transfer distribution model for stack simulation of solid oxide fuel cells. J. Phys. Conf. Ser. 2016, 745, 032148. [Google Scholar] [CrossRef]
- Onaka, H.; Iwai, H.; Kishimoto, M.; Saito, M.; Yoshida, H.; Brus, G.; Szmyd, J.S. Charge-transfer distribution model applicable to stack simulation of solid oxide fuel cells. Heat Mass Transf. 2018, 54, 2425–2432. [Google Scholar] [CrossRef]
- Mirzababaei, J.; Chuang, S.S.C. La0.6Sr0.4Co0.2Fe0.8O3 Perovskite: A Stable Anode Catalyst for Direct Methane Solid Oxide Fuel Cells. Catalysts 2014, 4, 146–161. [Google Scholar] [CrossRef] [Green Version]
- Lichtner, A.; Jauffrès, D.; Roussel, D.; Charlot, F.; Martin, C.; Bordia, R. Dispersion, connectivity and tortuosity of hierarchical porosity composite SOFC cathodes prepared by freeze-casting. J. Eur. Ceram. Soc. 2015, 35, 585–595. [Google Scholar] [CrossRef]
- Papurello, D.; Menichini, D.; Lanzini, A. Distributed relaxation times technique for the determination of fuel cell losses with an equivalent circuit model to identify physicochemical processes. Electrochim. Acta 2017, 258, 98–109. [Google Scholar] [CrossRef]
- Wilson, J.R.; Kobsiriphat, W.; Mendoza, R.; Chen, H.Y.; Hiller, J.M.; Miller, D.J.; Thornton, K.; Voorhees, P.W.; Adler, S.B.; Barnett, S.A. Three-dimensional reconstruction of a solid-oxide fuel-cell anode. Nat. Mater. 2006, 5, 541–544. [Google Scholar] [CrossRef] [PubMed]
- Iwai, H.; Shikazono, N.; Matsui, T.; Teshima, H.; Kishimoto, M.; Kishida, R.; Hayashi, D.; Matsuzaki, K.; Kanno, D.; Saito, M.; et al. Quantification of SOFC anode microstructure based on dual beam FIB-SEM technique. J. Power Sources 2010, 195, 955–961. [Google Scholar] [CrossRef]
- Kishimoto, M.; Iwai, H.; Saito, M.; Yoshida, H. Quantitative evaluation of solid oxide fuel cell porous anode microstructure based on focused ion beam and scanning electron microscope technique and prediction of anode overpotentials. J. Power Sources 2011, 196, 4555–4563. [Google Scholar] [CrossRef]
- Cayan, F.N.; Pakalapati, S.R.; Elizalde-blancas, F.; Celik, I. On modeling multi-component diffusion inside the porous anode of solid oxide fuel cells using Fick’s model. In Proceedings of the 6th International Conference on Fuel Cell Science, Engineering and Technology, Denver, CO, USA, 16–18 June 2008. [Google Scholar]
- Tan, W.C.; Iwai, H.; Kishimoto, M.; Brus, G.; Szmyd, J.S.; Yoshida, H. Numerical analysis on effect of aspect ratio of planar solid oxide fuel cell fueled with decomposed ammonia. J. Power Sources 2018, 384, 367–378. [Google Scholar] [CrossRef]
- Shikazono, N.; Kanno, D.; Matsuzaki, K.; Teshima, H.; Sumino, S.; Kasagi, N. Numerical Assessment of SOFC Anode Polarization Based on Three-Dimensional Model Microstructure Reconstructed from FIB-SEM Images. J. Electrochem. Soc. 2010, 157, B665–B672. [Google Scholar] [CrossRef]
- Kanno, D.; Shikazono, N.; Takagi, N.; Matsuzaki, K.; Kasagi, N. Evaluation of SOFC anode polarization simulation using three-dimensional microstructures reconstructed by FIB tomography. Electrochim. Acta 2011, 56, 4015–4021. [Google Scholar] [CrossRef]
- Rhazaoui, K.; Cai, Q.; Kishimoto, M.; Tariq, F.; Somalu, M.R.; Adjiman, C.S.; Brandon, N.P. Towards the 3D modelling of the effective conductivity of solid oxide fuel cell electrodes—Validation against experimental measurements and prediction of electrochemical performance. Electrochim. Acta 2015, 168, 139–147. [Google Scholar] [CrossRef]
- Suzue, Y.; Shikazono, N.; Kasagi, N. Micro modeling of solid oxide fuel cell anode based on stochastic reconstruction. J. Power Sources 2008, 184, 52–59. [Google Scholar] [CrossRef]
- Prokop, T.; Berent, K.; Iwai, H.; Szmyd, J.; Brus, G. A three-dimensional heterogeneity analysis of electrochemical energy conversion in SOFC anodes using electron nanotomography and mathematical modeling. Int. J. Hydrogen Energy 2018. [Google Scholar] [CrossRef]
- Kulikovsky, A.A. A model for SOFC anode performance. Electrochim. Acta 2009, 54, 6686–6695. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, R.; Min, T.; Kang, Q.; Tao, W. Pore-scale study of effects of macroscopic pores and their distributions on reactive transport in hierarchical porous media. Chem. Eng. J. 2018, 349, 428–437. [Google Scholar] [CrossRef]
- Hsu, T.; Epting, W.K.; Mahbub, R.; Nuhfer, N.T.; Bhattacharya, S.; Lei, Y.; Miller, H.M.; Ohodnicki, P.R.; Gerdes, K.R.; Abernathy, H.W.; et al. Mesoscale characterization of local property distributions in heterogeneous electrodes. J. Power Sources 2018, 386, 1–9. [Google Scholar] [CrossRef]
- Anselmi-Tamburini, U.; Chiodelli, G.; Arimondi, M.; Maglia, F.; Spinolo, G.; Munir, Z. Electrical properties of Ni/YSZ cermets obtained through combustion synthesis. Solid State Ion. 1998, 110, 35–43. [Google Scholar] [CrossRef]
- Bessette, N.F., II; Wepfer, W.J.; Winnick, J. A Mathematical Model of a Solid Oxide Fuel Cell. J. Electrochem. Soc. 1995, 142, 3792–3800. [Google Scholar] [CrossRef]
- De Boer, B. Hydrogen Oxidation at Porous Nickel and Nickel/yttria Stabilised Zirconia Cermet Electrodes. Ph.D. Thesis, Universiteit Twente, Enschede, The Netherlands, 1998. [Google Scholar]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. A new method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]







 | ||||
| Case | h | r | Case | h | r | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| - | - | - | - | ||||||||
| 0.0.0 | 5.48 | 0.44 | 2.52 | ||||||||
| center-type (non-conducting) | corner-type (non-conducting) | ||||||||||
| 1.1.1 | 0.75 | 0.00 | 5.48 | 0.44 | 2.41 | 2.1.1 | 1.50 | 0.00 | 5.48 | 0.44 | 2.41 |
| 1.1.2 | 1.50 | 0.00 | 5.45 | 0.44 | 2.42 | 2.1.2 | 3.00 | 0.00 | 5.44 | 0.44 | 2.43 |
| 1.1.3 | 2.35 | 0.00 | 5.39 | 0.44 | 2.50 | 2.1.3 | 4.50 | 0.00 | 5.33 | 0.43 | 2.56 |
| 1.1.4 | 3.00 | 0.00 | 4.27 | 0.43 | 2.72 | 2.1.4 | 6.00 | 0.00 | 5.12 | 0.41 | 2.87 |
| 1.1.5 | 3.75 | 0.00 | 5.09 | 0.41 | 3.29 | 2.1.5 | 7.50 | 0.00 | 4.75 | 0.39 | 3.66 |
| 1.2.1 | 0.75 | 3.75 | 5.48 | 0.44 | 2.43 | 2.2.1 | 1.50 | 3.75 | 5.47 | 0.44 | 2.46 |
| 1.2.2 | 1.50 | 3.75 | 5.43 | 0.44 | 2.45 | 2.2.2 | 3.00 | 3.75 | 5.40 | 0.43 | 2.55 |
| 1.2.3 | 2.25 | 3.75 | 5.32 | 0.43 | 2.62 | 2.2.3 | 4.50 | 3.75 | 5.21 | 0.42 | 2.77 |
| 1.2.4 | 3.00 | 3.75 | 5.10 | 0.41 | 2.91 | 2.2.4 | 6.00 | 3.75 | 4.85 | 0.39 | 2.67 |
| 1.2.5 | 3.75 | 3.75 | 4.74 | 0.39 | 4.10 | 2.2.5 | 7.50 | 3.75 | 4.29 | 0.36 | 4.10 |
| 1.3.1 | 0.75 | 7.00 | 5.48 | 0.44 | 2.46 | 2.3.1 | 1.50 | 7.50 | 5.47 | 0.44 | 2.47 |
| 1.3.2 | 1.50 | 7.00 | 5.43 | 0.44 | 2.47 | 2.3.2 | 3.00 | 7.50 | 5.32 | 0.43 | 2.50 |
| 1.3.3 | 2.25 | 7.00 | 5.32 | 0.44 | 2.62 | 2.3.3 | 4.50 | 7.50 | 5.20 | 0.42 | 2.82 |
| 1.3.4 | 3.00 | 7.00 | 5.10 | 0.43 | 2.72 | 2.3.4 | 6.00 | 7.50 | 4.78 | 0.39 | 2.92 |
| 1.3.5 | 3.75 | 7.00 | 4.75 | 0.41 | 3.94 | 2.3.5 | 7.50 | 7.50 | 4.04 | 0.34 | 4.47 |
| corner-type (ion-conducting) | |||||||||||
| 2.1.3 (YSZ) | 4.50 | 0 | 5.28 | 0.42 | 2.46 | ||||||
| 2.1.4 (YSZ) | 6.00 | 0 | 5.07 | 0.39 | 2.50 | ||||||
| 2.1.5 (YSZ) | 7.50 | 0 | 4.72 | 0.34 | 2.54 | ||||||
| 2.2.3 (YSZ) | 4.50 | 3.75 | 5.15 | 0.42 | 2.49 | ||||||
| 2.2.4 (YSZ) | 6.00 | 3.75 | 4.80 | 0.39 | 2.50 | ||||||
| 2.2.5 (YSZ) | 7.50 | 3.75 | 4.24 | 0.34 | 2.47 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prokop, T.A.; Berent, K.; Szmyd, J.S.; Brus, G. A Three-Dimensional Numerical Assessment of Heterogeneity Impact on a Solid Oxide Fuel Cell’s Anode Performance. Catalysts 2018, 8, 503. https://doi.org/10.3390/catal8110503
Prokop TA, Berent K, Szmyd JS, Brus G. A Three-Dimensional Numerical Assessment of Heterogeneity Impact on a Solid Oxide Fuel Cell’s Anode Performance. Catalysts. 2018; 8(11):503. https://doi.org/10.3390/catal8110503
Chicago/Turabian StyleProkop, Tomasz A., Katarzyna Berent, Janusz S. Szmyd, and Grzegorz Brus. 2018. "A Three-Dimensional Numerical Assessment of Heterogeneity Impact on a Solid Oxide Fuel Cell’s Anode Performance" Catalysts 8, no. 11: 503. https://doi.org/10.3390/catal8110503
APA StyleProkop, T. A., Berent, K., Szmyd, J. S., & Brus, G. (2018). A Three-Dimensional Numerical Assessment of Heterogeneity Impact on a Solid Oxide Fuel Cell’s Anode Performance. Catalysts, 8(11), 503. https://doi.org/10.3390/catal8110503