Quantitative Phase Analysis by X-ray Diffraction—Doping Methods and Applications
Abstract
:1. Introduction
2. Essential Points in Short
3. Chung’s Matrix Flushing Method
4. Doping Methods
4.1. Simultaneous Determination of the Fractions of Several Phases Using A Single Doping
4.2. Determination of the Fraction of the Dominant Phase
- –
- the diffraction pattern of the original sample, measuring IX,
- –
- the diffraction pattern of the sample doped by a known fraction, Xa, measuring IX d+a,
- –
- the diffraction pattern of the pure phase X, measuring IX0.
4.3. A New Application of the Doping Method
- –
- quenching the alloy from HT to room temperature (RT), in order to stop or essentially slow down the decomposition process,
- –
- doping the quenched alloy by a substance having the same (or very similar) chemical composition and crystal structure as the precipitate, that is, Zn instead of β(Zn) in case of Al–Zn alloys,
- –
- taking into account a possible (although very slow) continuation of the decomposition process at RT.
4.4. Remarks on the Doping Methods
5. The Rietveld Approach
6. Round Robin on Quantitative Phase Analysis
- –
- the types of analysis: measurement of integrated intensities, diffraction line profile fitting,
- –
- the Rietveld method, application of different methods in QPA, the use of database of observed patterns, etc.
- –
- sources: laboratory and synchrotron X-rays, neutron reactor radiation
- –
- the aim: determination of phase fractions from diffraction data.
- –
- to document powder diffraction techniques commonly applied in QPA
- –
- to assess levels of accuracy, precision, and limits of detection
- –
- to identify problems and suggest solutions
- –
- to formulate recommended procedures for QPA using diffraction data
- –
- to create a standard set of samples for future reference.
- –
- simple three-phase sample (corundum, fluorite, zincite)
- –
- sample containing an amorphous phase
- –
- sample with a phase showing preferred orientation
- –
- sample exhibiting a problem of microabsorption
- –
- complex synthetic and natural mineral phases
- –
- pharmaceutical samples.
- –
- the major difficulty is caused by the lack of the operator expertise, which becomes more apparent with more complex samples
- –
- some of these samples introduced the requirement for skill and judgement in sample preparation techniques
- –
- a great obstacle to accurate QPA for X-ray diffraction based methods is the presence of absorption contrast between phases (microabsorption), which often cannot be solved.
7. Selected Studies with Application of Doping Methods
8. Phase Transitions in Titanium Dioxide
9. Biomineralization Processes in Ostrea edulis
10. Crystalline Phases in Intermetallic Oxides
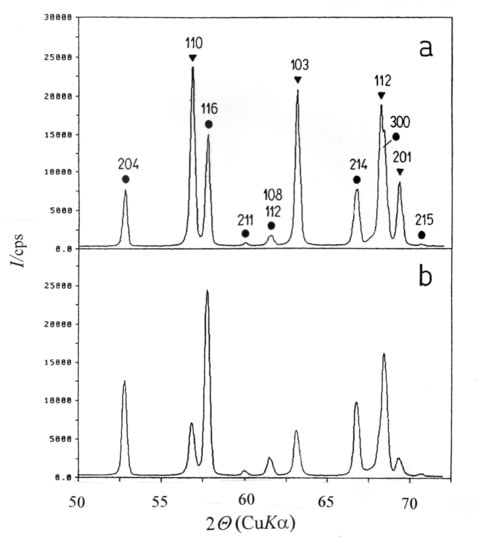
11. Microstructure of Al–Zn Alloys
12. Conclusions
Acknowledgments
Conflicts of Interest
References
- Alexander, L.E.; Klug, H.P. X-ray diffraction analysis of crystalline dusts. Anal. Chem. 1948, 20, 886–889. [Google Scholar] [CrossRef]
- Klug, H.P.; Alexander, L.E. Qualitative and Quantitative Phase Analysis. In X-ray Diffraction Procedures, 2nd ed.; John Wiley: New York, NY, USA, 1974; pp. 505–565. [Google Scholar]
- Madsen, I.C.; Scarlett, N.V.Y.; Kleeberg, R.; Knorr, K. Quantitative phase analysis. In International Tables for Crystallography, Volume H, Powder Diffraction, 1st ed.; Gilmore, C.J., Kaduk, J.A., Schenk, H., Eds.; International Union of Crystallography: Chester, UK, 2019; pp. 344–373. [Google Scholar] [CrossRef]
- Chung, F.H. Quantitative interpretation of X-ray diffraction patterns of mixtures. I. Matrix-flushing method for quantitative multicomponent analysis. J. Appl. Cryst. 1974, 7, 519–525, 526–531. [Google Scholar] [CrossRef]
- Chung, F.H. Quantitative interpretation of X-ray diffraction patterns of mixtures. III. Simultaneous determination of a set of reference intensities. J. Appl. Cryst. 1975, 8, 17–19. [Google Scholar] [CrossRef]
- Popović, S.; Gržeta-Plenković, B. The doping method in quantitative X-ray diffraction phase analysis. J. Appl. Cryst. 1979, 12, 205–208. [Google Scholar] [CrossRef]
- Popović, S.; Gržeta-Plenković, B.; Balić-Žunić, T. The doping method in quantitative X-ray diffraction phase analysis. Addendum, J. Appl. Cryst. 1983, 16, 505–507. [Google Scholar] [CrossRef] [Green Version]
- Popović, S.; Gržeta-Plenković, B. Dilution and addition methods in quantitative X-ray diffraction phase analysis. In Advanced Methods in X-ray and Neutron Structure Analysis in Materials Science; Hašek, J., Ed.; Plenum Press: New York, NY, USA, 1989; pp. 29–41. [Google Scholar]
- Gržeta, B.; Popović, S.; Toraya, H. DOP-FIT method for quantitative analysis of multicomponent powders. Mater. Sci. Forum 1996, 228–231, 49–54. [Google Scholar] [CrossRef]
- Popović, S. Quantitative phase analysis by X-ray diffraction – simple routes. Maced. J. Chem. Chem. Eng. 2015, 34, 33–38. [Google Scholar] [CrossRef] [Green Version]
- Popović, S. Quantitative Phase Analysis by XRD–Simple Routes–New Perspectives/Applications. In 26th Croatian-Slovenian Crystallographic Meeting, Book of Abstracts; Poreč, C., Matković Čalogović, D., Eds.; Croatian Academy of Sciences and Arts: Zagreb, Croatia, 2018; p. 12. [Google Scholar]
- Skoko, Ž.; Popović, S.; Štefanić, G. Microstructure of Al–Zn and Zn-Al alloys. Croat. Chem. Acta 2009, 82, 405–420. [Google Scholar]
- Skoko, Ž.; Popović, S. Microstructure of Al-Cu, Al–Zn, Al-Ag-Zn and Al–Zn-Mg Alloys. In Encyclopedia of Aluminum and Its Alloys; Totten, G.E., Ed.; Taylor & Francis: New York, NY, USA, 2018; pp. 1659–1674. [Google Scholar] [CrossRef]
- Young, R.A. The Rietveld Method; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Scardi, P. IUCr Commission on Powder Diffraction News; International Union of Crystallography: Chester, UK, 2000; p. 24. [Google Scholar]
- Madsen, I.C.; Scarlett, N.V.; Cranswick, L.M.; Lwin, T. Outcomes of the International Union of Crystallography Commission on Powder Diffraction Round Robin on Quantitative Phase Analysis: Samples 1a to 1h. J. Appl. Cryst. 2001, 34, 409–426. [Google Scholar] [CrossRef] [Green Version]
- Scarlett, N.V.Y.; Madsen, I.C.; Cranswick, L.M.; Lwin, T.; Groleau, E.; Stephenson, G.; Aylmore, M.; Agron-Olshina, N. Outcomes of the International Union of Crystallography Commission on Powder Diffraction Round Robin on Quantitative Phase Analysis: Samples 2, 3, 4, synthetic bauxite, natural granodiorite and pharmaceuticals. J. Appl. Cryst. 2002, 35, 383–400. [Google Scholar] [CrossRef]
- Gajović, A.; Furić, K.; Tomašić, N.; Popović, S.; Skoko, Ž.; Musić, S. Mechanochemical preparation of nanocrystalline TiO2 powders and their behavior at high temperatures. J. Alloys Compd. 2005, 398, 188–199. [Google Scholar] [CrossRef]
- Popović, S.; Tonejc, A.; Skoko, Ž. Contemporary diffraction methods in study of polycrystals. Croat. Chem. Acta 2015, 88, 561–577. [Google Scholar] [CrossRef] [Green Version]
- Medaković, D.; Hrs-Brenko, M.; Popović, S.; Gržeta, B. X-ray diffraction study of the first larval shell of Ostrea edulis. Mar. Biol. 1989, 101, 205–209. [Google Scholar] [CrossRef]
- Medaković, D.; Popović, S.; Gržeta, B.; Plazonić, M.; Hrs-Brenko, M. X-ray diffraction study of calcification processes in embryos and larvae of the brooding oyster Ostrea edulis. Mar. Biol. 1997, 129, 615–623. [Google Scholar] [CrossRef]
- Ristić, M.; Popović, S.; Musić, S. X-ray diffraction and Mössbauer spectra of the system Fe2O3-Eu2O3. J. Mater. Sci. Lett. 1990, 9, 872–875. [Google Scholar] [CrossRef]
- Musić, S.; Popović, S.; Ristić, M.; Ilakovac, V. X-ray powder diffraction study of Fe2O3-M2O3, M=Ga, In, Eu, Gd. Vestn. Slov. Kem. Drus. 1992, 39, 383–397. [Google Scholar]
- Musić, S.; Ilakovac, V.; Ristić, M.; Popović, S. Formation of oxide phases in the system Fe2O3-Gd2O3. J. Mater. Sci. 1992, 27, 1011–1015. [Google Scholar] [CrossRef]
- Musić, S.; Popović, S.; Czakó-Nagy, I.; Gashi, F. Formation of oxide phases in the system Fe2O3-Gd2O3. Part II. J. Mater. Sci. Lett. 1993, 12, 869–873. [Google Scholar] [CrossRef]
- Ristić, M.; Popović, S.; Czakó-Nagy, I.; Musić, S. Formation and characterization of oxide phases in the Fe2O3 - Eu2O3 system. Mater. Lett. 1996, 27, 337–341. [Google Scholar] [CrossRef]
- Ristić, M.; Nowik, I.; Popović, S.; Musić, S. Formation of oxide phases in the system Eu2O3-Fe2O3. Croat. Chem. Acta 2000, 73, 525–540. [Google Scholar]








© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popović, S. Quantitative Phase Analysis by X-ray Diffraction—Doping Methods and Applications. Crystals 2020, 10, 27. https://doi.org/10.3390/cryst10010027
Popović S. Quantitative Phase Analysis by X-ray Diffraction—Doping Methods and Applications. Crystals. 2020; 10(1):27. https://doi.org/10.3390/cryst10010027
Chicago/Turabian StylePopović, Stanko. 2020. "Quantitative Phase Analysis by X-ray Diffraction—Doping Methods and Applications" Crystals 10, no. 1: 27. https://doi.org/10.3390/cryst10010027
APA StylePopović, S. (2020). Quantitative Phase Analysis by X-ray Diffraction—Doping Methods and Applications. Crystals, 10(1), 27. https://doi.org/10.3390/cryst10010027