Reproducible Orientation Relationships Developed from Phase Transformations—Role of Interfaces

Abstract

The orientation relationship (OR) between phases related by a phase transformation is often reproducible. This study interprets and predicts the reproducible ORs with a two-stage approach. The initial OR formed at the nucleation stage tends to allow a periodic structure of a preferred state to form in the interface. A matching correspondence of either a one-to-one or n-to-m nature can be specified in the periodic structure. An initial OR will become the final reproducible OR if there is no misfit. Otherwise, a reproducible OR developed at the growth stage tends to permit a singular dislocation structure to form in an interface where the preferred state must be sustained locally. The actual change in the OR is subject to the given material system and the phase-transformation condition. Various singular dislocation structures and their constraints on the ORs are analyzed, with thermodynamics and kinetics applied conceptually. The resulting ORs can be specified by following one or more Δg parallelism rules. A set of workable steps is provided to facilitate the interpretation of observed reproducible ORs. Some unsolved problems are identified, which call for further studies that can quantitatively combine the thermodynamics, kinetics and crystallography of phase transformations.

1. Introduction

The crystallography of a structural phase transformation in a crystalline material concerns the orientation relationship (OR) between the product and matrix phases and the morphology of the product phase expressed on the crystal basis of both phases. These important features in the microstructure after a phase transformation have received increasing attention due to the advancement of transmission electron microscopes (TEMs) and scanning electron microscopes (SEMs) equipped with electron backscatter diffraction (EBSD) equipment, which greatly facilitates the acquisition of crystallographic data. In most phase-transformation systems, the ORs and morphologies are reproducible, indicating naturally preferred selection during the phase transformations. Similar to the natural shape of a single crystal, the morphologies of a product phase are often characterized by faceted interfaces. In contrast to the case of a single crystal in which the crystal structure determines the orientation of the faceted surfaces, it is the formation of faceted interfaces that governs the OR in a phase-transformation system. This is due to the link between the structure of an interface and the geometry of the interface, including the OR and interface orientation. The general relationships between the interfacial structures and geometry of interfaces are explained in well-known books on interfaces in crystalline materials by Sutton and Balluffi [1] and by Howe [2]. When the product phase is free to select the OR, the selection normally favors the formation of a low-energy interfacial structure. Various models have been proposed for associating the ORs with preferred interfaces, as reviewed previously [3,4]. While many approaches have shown a certain degree of success in the interpretation of the ORs, their predictive power is limited. One reason is that most approaches concern only the two crystals separated by the interfaces, but other factors, such as transformation temperature, may affect the development of the OR during the phase-transformation process. Unfortunately, very few experimental data about the evolution of the OR and morphology during a phase transformation are available. To provide further insights into phase-transformation crystallography, it is still worth tracing back the OR development in a phase-transformation process.

According to the classification by Christian [5], a structural phase transformation may proceed either homogeneously or heterogeneously. A homogeneous transformation usually relates phases in which at least one set of lattice sites is almost identical. Typical examples are spinodal decomposition and some order–disorder transformations. In such a transformation, the OR will retain a set of lattice sites being shared by the lattices of the two phases. The resulting OR will enable the corresponding lattice vectors to be parallel, which is obvious and understandable. This paper does not further consider this type of phase transformation. Instead, it focuses on the more complicated heterogeneous transformations.

A heterogeneous transformation involves two stages, i.e., the nucleation and growth of the product phase. Unless the structures of two phases are almost identical, similar to the case of a homogeneous transformation, it is not always reasonable to assume that the nucleation and growth stages will favor the same OR. A measured OR and morphology should reflect the combined results due to both nucleation and growth stages. The present study provides a general approach to separately analyzing the development of the OR at the nucleation and growth stages of a phase transformation, in which the product phase can be either an equilibrium or a metastable phase. This two-stage approach facilitates the examination of the effects of thermodynamics and kinetics, with sophisticated theories for these stages, on phase-transformation crystallography. The influences of thermodynamics and kinetics factors on crystallography at these two stages is discussed conceptually, with a hope of inspiring a future consolidation of the thermodynamics, kinetics, and crystallography of a phase transformation. It is believed that with the progress in consolidation, the simulation of microstructural evolution, which is now mainly based on thermodynamics and kinetic models, will become more realistic and predictive.

2. Nucleation Stage

2.1. Thermodynamic and Kinetic Considerations

The thermodynamics and kinetics of nucleation theories of solid-state phase transformations are much more advanced than the crystallography of nucleation, and these theories lay the fundamentals for us to understand the nucleation process. As is well-known from textbooks on phase transformations in metals (e.g., [6,7]), the nuclei that actually form in a phase transformation are those that can form most rapidly. Among the various variables that determine the nucleation rate, the most prominent parameter is the nucleation barrier, usually denoted by ΔG*. This barrier is mainly due to the generation of an interface, which initiates as a cluster of atoms organized into a structure towards the product phase in an embryo. By assuming that the nucleus is a sphere with isotropic interfacial energy per unit area, γ, ΔG* is expressed by [6]:

ΔG* = 16πγ³/[3(ΔG_v − ΔG_s)²]

(1)

where ΔG_v is forced matching in the interfacial structure. The formation of nuclei with the smallest γ is the most effective way to minimize ΔG*, on the condition that the possible rise in ΔG_s does not override the effect of γ. In general, interfacial energy is not isotropic. A nucleus associated with a small overall interfacial energy and a small ΔG_s tends to survive and proceed into the growth stage. In practice, heterogeneous nucleation at preexisting interfaces often occurs, since replacing a certain part of a preexisting interface may reduce the rise in interfacial energy due to nucleation. In addition, the disordered structure possibly existing in the preexisting interfaces may provide an easy path for the misfit strain to be relaxed through. For simplicity, however, we first limit the systems to those consisting of only the product and matrix phases related by the phase transformation, so that the interfaces under consideration are only those between these two phases. The effects of other interfaces on the development of the OR will be considered later. This does not necessarily mean a homogenous nucleation, since, strictly speaking, nucleation near a dislocation or point defect should be considered as a heterogeneous nucleation process and the possible influences of these defects on the phase transformations are not excluded.

The value of γ of an interface depends on its structure. The individual bonds across the interface defining the interfacial structure are related to the compositions and structures of both phases, as well as the possible segregation in the interface. In addition, the arrangement of atoms near the interface is affected by the macroscopic geometry of the interface, including the OR and the orientation of the interface. Assuming that there is no long-range misfit strain, at a given temperature, there is an equilibrium shape so that ∑γdA = the minimum for each OR, as can be determined by the Wulff construction. Various equilibrium shapes for nuclei in different cases have been reviewed in some detail by Aaronson et al. [7]. Provided that the equilibrium shapes are maintained by nuclei with different ORs, the nuclei with ORs associated with smaller values of ∑γdA will have higher probabilities of reaching the growth stage than those with higher values [7]. Therefore, the OR(s) developed at the nucleation stage is/are those that provide the geometry for smaller values of ∑γdA. Unfortunately, experimental data of γ as a function of interfacial geometry are rather limited. In principle, it is possible to calculate γ as a function of interfacial geometry. The major calculation methods and results for γ are applicable to rational interfaces (parallel to some low-index planes), as reviewed by Howe [2]. A method for calculating the γ of irrational interfaces was recently proposed by Dai and Zhang [8]. With this method, equilibrium cross sections enclosed by irrational interfaces were determined according to the Wulff construction based on the results of γ for different ORs [9]. Nevertheless, it is difficult to verify the equilibrium shape experimentally, since the observed shape may be governed by anisotropic growth kinetics. The application of the Wulff construction for determining equilibrium shapes usually requires the system to be free of misfit strain [2,7,9]. However, misfit strain usually exists at the nucleation stage. It is a challenge to correctly describe the misfit-strain field at this stage, since this field is affected by the OR, which may vary at this stage. In addition, to calculate the ΔG_s associated with a nucleus of small size, the conventional elastic theory may not be valid. While it is unreasonable to neglect the effect of misfit strain, for the purpose of explaining the observed ORs, we assume that the driving force is large enough for a low γ interface to form at the expense of increasing the misfit strain to a certain degree. Thus, the following analysis of the preferred OR will focus on the effect of interfacial energy as the governing factor.

To analyze the general tendencies in the development of the OR during nucleation, it is convenient to apply a common treatment: to separate γ into two components [2]: a structural component due to the distortion of bonds and a compositional component due to the unfavorable compositional bonds if the compositions of the two phases are different. In a system consisting of ceramic phases or intermetallic compounds, the compositional component of γ may strongly vary with the interface orientation with respect to one or both phases. The structural component is sensitive to the degree of misfit between lattices across the interface, and this is greatly affected by the OR. A preferred OR tends to provide the geometry for an interface to be associated with a local minimum in the structure component. If both phases are solid-state solutions of metal phases, such as fcc, hcp, or bcc metals, the compositional component is largely independent of the interfacial geometry. In such a system, the development of the interfacial geometry during nucleation is probably dominated by the minimization of the structural component of γ. That is why the same preferred interfacial geometry has been observed in alloys of completely different compositions (e.g., near the Kurdjumov–Sachs (K-S) OR and {112}_fcc habit planes in steels [10,11] and Cr-Cu alloys [12,13]). In general, it is conceivable that the development of ORs always tends to reduce the structural component in γ, though the weight of this component in γ may vary from one system to another. The analysis below is based on the hypothesis that the development of the preferred interfacial geometry is mainly driven by the local minimization of the structural component of γ. With a compromise, such a preferred OR may be compatible with the interface preferred by the local minimization of the compositional component. Namely, the compositional component can be incorporated to limit the range of interfacial geometry among the candidates selected according to the local minimization of the structural component, whenever necessary.

The structural component of γ is closely related to the degree of matching or coherency in the interfacial structure. It is commonly agreed that a coherent structure has the lowest γ, while an incoherent interface has a high γ. One can see a remarkable difference from the data provided by Howe [2] (i.e., coherent: 5–200, semicoherent: 200–800, and incoherent: 800–2500, with units of mJ/m²). To obtain a low energy, the interface between a surviving nucleus and its matrix tends to have a coherent structure, even withstanding a certain degree of misfit strain when the lattice parameters of the two phases do not permit perfect coherent matching. This tendency is confirmed by observations of coherent precipitates in systems in which both phases have the same structure and similar lattice parameters (e.g., fcc Co precipitated from a Cu matrix [14]). For such a special case, the unique (cubic/cubic) OR always holds between the two phases to enable the coherent structure in all portions of the interface surrounding the product phase.

In many phase-transformation systems, the crystal structure of the product phase is significantly different from that of the matrix. To reduce the interfacial energy, the nucleus also tends to be as coherent with the matrix as possible. It is often impossible to specify a unique OR for such a coherent nucleus. Imagine that the nucleus is enclosed by different coherent facets at the atomic scale. Sharing a lattice plane from each phase at a local facet implies parallelism of the planes from adjacent phases. Generally, when a lattice plane in one crystal is parallel to a lattice plane in the other crystal, other planes of the two crystals may not be parallel simultaneously unless the crystals are distorted. As a result of the distortion, parallelism may hold between different pairs of planes at different facets. Meanwhile, the corresponding descriptions of the ORs are also different for a single nucleus. For the convenience of further discussion, we classify two types of initial ORs formed at the nucleation stage. One type of initial OR is called the invariant OR. With an invariant OR, the parallelism of different planes or directions at any parts of the interface surrounding a nucleus can be defined by a unique OR, such as the cubic/cubic OR relating two fcc phases. The parallelism condition can hold regardless of whether there is a misfit between the two lattices. The other type of OR is the variant OR, which will vary along the interface according to local parallelism at different locations of the interface.

2.2. Matching Correspondence and Preferred State

Considering the nature of variant ORs and the possible variations of the OR at the time scale, it is improper to specify a unique initial OR developed at the nucleation stage in a general system. However, the initial OR must be confined to a certain range for the interface to form an energetically preferred matching structure, e.g., one-to-one coherency. Therefore, the matching correspondence is an intrinsic characteristic in an interfacial structure initiated from the nucleation stage. This characteristic is sustained throughout the growth stage. For example, the matching correspondence in a coherent interface between a nucleus and matrix can be preserved in the coherent regions between misfit dislocations in a semicoherent interface of a precipitate during growth. Such a matching correspondence imposes a restriction on the range of the OR that may change at the growth stage. It also serves as an essential reference for calculations of the interfacial dislocations and strain energy.

In addition to the one-to-one matching correspondence in a coherent structure, there are other preferred matching correspondences. When the lattice parameters of the two phases are significantly different, the one-to-one correspondence usually does not relate nearby lattice points that are more likely to become matching pairs. In such a system, the surviving nuclei are still those that can orientate themselves so that the interfacial energy can be minimized locally, though the matching correspondence in the low-energy interfacial structure is not one to one. To describe such an interfacial structure associated with a local energy minimum in a general case, Bollmann [15] called it a preferred state. Accordingly, a preferred state of an interface is characterized by a periodic interfacial structure, in which the repeated structural units carry a certain feature of matching. According to the matching correspondence, Bollmann [15] classified two types of preferred state. The primary preferred state is a structure of full coincidence in three dimensions (3D) that corresponds to one-to-one matching correspondence. The structural units in either phase can be used to represent the structural units of this preferred state. Though the structural units in the two phases are usually different, similar bond topologies of the units in different phases can form by a small local distortion to ensure a one-to-one matching correspondence locally in 3D. A secondary preferred state is a fractional coincidence state, and it reflects an n-to-m matching correspondence at least in 2D (where n and m are integers, and usually, n ≠ m). The n-to-m matching correspondence means that one point in every n points in one lattice matches one point in every m points in the other lattice. In 3D, the meaning of n or m is similar to that of ∑ for coincidence site lattice (CSL) grain boundaries, where ∑ = the ratio of the unit cell of the CSL to that of the crystal lattice. A structural unit in a secondary preferred state is usually different from those in both phases.

Bollmann’s classification is adopted in the present study. This classification of the structures of the preferred states greatly simplifies the analysis of different matching correspondences, without a need to specify the structural units of the preferred states. It also underlines the main difference between the interfacial structures in the two types of preferred states. One can understand the difference between these two types of states as an analogy to the structures in grain boundaries. Namely, the primary preferred state exists in the coherent regions between dislocations in a small-angle grain boundary. A secondary preferred state corresponds to the periodic structure in a low ∑ large-angle grain boundary. Our experience of the study of heterophase interfaces in secondary preferred states indicates that it is often more appropriate to define the latter in 2D, i.e., in a specific preferred interface. This implies that the structural units distribute periodically only in the interface plane. However, the repeated structural unit remains a 3D cell, which is an intrinsic unit of the periodic structure of the preferred state, in accordance with the conventional description of structural units in CSL grain boundaries [1,2]. For convenience, we will call the pair of overlapped lattice planes in which a secondary preferred state is to form the planes of the secondary preferred state. Note that the 3D structural units in the interfaces may not be the same, even if different ORs can yield the identical patterns in the same pair of overlapped planes. As a result, a periodic matching structure in 2D may correspond to different preferred states. To clarify the existence of different preferred states, one can compare the matching patterns in a plane normal to the planes of the secondary preferred state corresponding to different ORs. However, to distinguish their preference order, a study of the energy of the structural units is needed.

Though the detailed atomic structure of the structural units of a secondary preferred state is usually unknown, the matching correspondence can be derived from a CSL in 2D by assuming exact matching. This CSL must have the same periodicity as the secondary preferred state. In real materials, a fully coincidence-coherent structure is rare. It is often convenient to force one lattice to deform so that a constrained CSL (CCSL) can be built [16]. In the 2D CCSL on the planes of the secondary preferred state, each row of dense CCSL defines a pair of the matching vectors. Among these pairs, we may select one to specify the parallelism of two vectors. Thus, in terms of the parallelism of two rational planes for the 2D CCSL and two rational directions along a row of dense CCSL points, we obtain an initial OR developed at the nucleation stage. This OR may serve as the representative OR for the further development at the growth stage. Because the planes of the secondary preferred state must be parallel to each other, the representative OR partially fixes the OR. If, at this OR, the vectors in the matching pairs can be simultaneously parallel to each other according to the crystal structures of the two phases, the OR is invariant. Otherwise, the OR is variant in the plane, but there are only a few choices of representative rational ORs. Therefore, the initial OR corresponding to a secondary preferred state is at least partially invariant. Because any further adjustment of the OR at the growth stage is usually very small (as explained later), close to the measurement uncertainty, finding the expression of the representative rational OR is a crucial step for understanding the reproducible OR observed in a system in a secondary preferred state. This is different from a system in the primary preferred state. One may use different combinations of parallel planes and parallel directions for the representative rational ORs corresponding to the same primary preferred state. However, the OR at the growth stage may change wildly, and its interpretation is rather challenging.

2.3. Prediction of Matching Correspodences and Representative ORs

The periodic feature of a preferred state implies that the structures of preferred states must be discrete, as indicated by Bollmann [15]. A simple way to identify potential preferred states is to check for the possible existence of periodicity in the structure at local regions of an interface. This can be done by examining the distribution of geometric matching between two rigid lattices. When two lattices are overlapped (in 2D) or interpenetrated (in 3D), a pattern of good and poor matching will form, as demonstrated by Bollmann in his early book that introduces the O-lattice theory [17] (which provides a set of lattices in transparent sheets to enable the readers to see the patterns). If the displacement between the nearest neighboring points from different lattices is sufficiently small, these points can be regarded as matching pairs. Let one of the points in a matching pair define a good matching site (GMS), usually in the larger lattice for efficiency. When GMSs form clusters, comprising densely and periodically distributed GMSs, a preferred state is likely to form from these clusters. The connection between clusters of continuous GMSs and coherent regions is implied in various geometric models, such as the O-lattice model [17] and structural-ledge model [13,18]. Such a connection between the good-matching regions of rigid lattices and coherent regions is implied in the classic dislocation model of twist grain boundaries, as well-described in many textbooks [1,2,5,6]. By selecting a proper good-matching criterion guided by real interfaces, such as small-angle grain boundaries, one can search for the existence of GMS clusters [19].

Based on the connection between the GMS clusters in the rigid model and a preferred state in a real interface, one can specify the OR that permits a potential preferred state once the GMS clusters are identified. A near-row-matching method [20] has been suggested for a fast and systematic search. This method mainly consists of two simple steps. In the first step, a row of dense GMSs is searched, based on a one-to-one or n-to-m lattice-point correspondence between lattice-point rows from different lattices, as illustrated by the artificial 1D lattices in Figure 1. In this figure, the points of the different lattices, represented by solid (blue) and open (red) circles (color online), are overlapped with one point from each lattice located at the origin. If the distances between neighboring points in the rows are smaller than a selected good-matching criterion (15% of the distance between points in the smaller lattice is used here, but 25% is recommended for the good-matching coefficient when the misfit is large), the neighboring point pair is regarded as a GMS, as marked by a large (green) circle. The direction of a good-matching row is defined by a pair of vectors, when a GMS-row segment consisting of at least three dense GMSs can form in the overlapped rows along these vectors. Both examples in Figure 1 meet the above condition. The resulting matching correspondence in 1D is one-to-one in Figure 1a and two-to-three in Figure 1b, respectively. After determining the good-matching direction, the second step is to search for the plane containing near-matching rows along the good-matching direction. In this step, the spacings between the rows along the determined parallel vectors in different lattices are compared. If the difference in the row distances is smaller than a selected good-matching criterion, the selected rows are regarded as nearly matching. Then, in the overlapped planes containing the nearly matching rows, one needs to examine whether the GMS-row segments in different rows can connect each other to form a cluster consisting of a 2D periodic GMS pattern. If such a cluster exists locally around the origin, the matching pairs in this cluster define the matching correspondence in 2D for the potential preferred state. The OR is specified by the parallelism of the good-matching vectors defined in the first step, and by the parallelism of the two planes determined in the second step. It is helpful to express the representative OR with the parallel vectors of matching pairs, i.e., with specific indexes (not unit vectors), so that the OR can carry the message of the matching correspondence. Note that an expression in terms of parallelism may yield two ORs, since the parallelism condition might imply both parallel and anti-parallel conditions, which may or may not yield crystallographic equivalent ORs, as explained by Du et al. [21]. When the ORs are not crystallographically equivalent but permit the existence of a 2D periodic GMS pattern, one expects different preferred states in the same parallel planes containing the same GMS-row segments, because the 3D structural units in the periodic structures of the preferred states are different relative to the distinct ORs. Different ORs corresponding to similar representative ORs have been observed in some systems (see examples in Section 3.2.2). This indicates the importance of the good matching in 2D, and the limited effect of the difference in the structural units in these systems.

Two examples are given below. The first example is simple, an extension of the 1D lattice in Figure 1a to 3D to form a pattern by interpenetrating two simple cubic structures, as seen in Figure 2. On the one hand, Figure 2a can be regarded to show the overlapped lattice points projected along the good-matching direction. As expected, one finds good matching between the nearest rows from each lattice. On the other hand, this figure can be viewed as the matching pattern in the plane containing the near-matching rows, with the good-matching direction in the horizontal direction and the near-matching rows aligned in the vertical direction. In this plane, the GMSs form clusters (the GMSs are marked by green circles in Figure 2b). One can see one-to-one matching in the GMS cluster around the origin. The clusters are distributed periodically in this plane, as shown in Figure 2c, over a large range. The predicted OR is the cubic/cubic OR. Due to the common symmetry and small misfit between the lattice constants, this OR permits one-to-one matching correspondence in 3D in the GMS cluster around the origin. Therefore, as expected, the primary preferred state will form in the regions of GMS clusters.

The second example is from a real case between a Mg₂Sn precipitate (fcc) and Mg matrix (hcp) in a Mg alloy [22]. This example is used to demonstrate that row matching is not always a sufficient condition for a GMS segment to repeat in the vicinity of the origin. Therefore, an examination of the existence of GMS clusters and the periodic structure in a cluster is necessary for predicting a preferred state. In this system, good matching is found between vectors of [4 5 1 0]_α/3 and [1 1 2]_β/2, so good-matching-row segments can be defined along the direction parallel to these vectors. Figure 3a,b are projected lattice points along the [4 5 1 0]_α and [1 1 2]_β directions, respectively. Therefore, each point in these figures represents an edge-on row. Some circles are drawn close to the origin, with their radii defining the spacings between rows. The latter are compared, and two pairs of close values are identified, as shown by the arrows and circles (red and blue, color online) in Figure 3a,b. Coincidentally, the two pairs of near-matching rows lie in the same direction along dense rows. One of the lattices, e.g., the fcc lattice, is rotated so that the planes containing the near-matching rows, (0 0 0 1)_α and (1 1 1)_β, become parallel (i.e., to arrange the arrows to be parallel in Figure 3c). The resulting interface is parallel to these planes. The GMS distribution is checked in the interface, as seen in Figure 3d. In this figure, a horizontal row of GMSs is along the parallel directions of [4 5 1 0]_α and [1 1 2]_β, showing good matching between [4 5 1 0]_α/3 and [1 1 2]_β/2. Due to the misfit along the matching rows, and GMS row segments must exist somewhere in the rows that are nearly matching, i.e., in the rows close to the origin. However, in this example, such a GMS row in the nearest near-matching rows does not repeat in the vicinity of the origin. Instead, GMSs in the distant near-matching rows can form a periodic pattern in the GMS cluster around the origin. Though there are only two GMSs in the next row, the number is increased if 25% rather than 15% is used for the good-matching coefficient. The use of 15% can better illustrate the special feature in this example, namely, the coexistence of three matching pairs of <4 5 1 0>_α/3 and <1 1 2>_β/2. This is because of the six-fold symmetry in the planes of (0 0 0 1)_α and (1 1 1)_β. In this example, a three-to-seven matching correspondence is found in the GMS cluster in 2D around the origin. It confirms the existence of a secondary preferred state in the observed interface parallel to (0 0 0 1)_α and (1 1 1)_β [22]. The matching correspondence in 2D can be defined by relating two of the three matching pairs (<4 5 1 0>_α/3 and <1 1 2>_β/2) in the cluster around the origin. The representative OR is expressed by (0 0 0 1)_α//(1 1 1)_β and [4 5 1 0]_α/3//[1 1 2]_β/2. Similar to in Figure 2c, a periodic distribution of the GMS clusters is seen in Figure 3e. The GMS row in the adjacent near-matching rows appears at a large distance from the origin, and hence, it belongs to another GMS cluster. The spacing between the nearest near-matching rows is an important parameter, since it defines the height of the possible steps, which links the GMS-row segments in the adjacent rows, as seen in Figure 3e. These steps are often present in the side facets at the edges of a precipitated plate. A plate with a truncated triangular shape is marked in Figure 3f. The major interface of the plate is parallel to (0 0 0 1)_α and (1 1 1)_β, with the OR close to the above representative OR. One can see the agreement between the orientation of a side facet (F1, F2 and F3) of the plate and the average orientation of a line (in the same color) passing GMS-row segments linked by the steps. The slight difference between the observed reproducible OR and the representative rational OR is related to the stepped structure, as will be explained in Section 3.2. A more detailed quantitative analysis of this case can be found in [22].

For a given system, the near-row-matching method usually yields multiple predictions for candidate preferred states. Even with the fixed result of the first step, there are still multiple ORs corresponding to various planes of secondary preferred states. For example, there is another observed OR defined by a parallelism between [4 5 1 0]_α/3 and [1 1 2]_β/2, but with (0 0 0 1)_α and (1 1 0)_β [23]. While this OR can also be predicted by the near-row-matching method, some ORs with better row matching were not observed. Note that in both cases, the observed interfaces are parallel to low-index planes. This natural tendency indicates the preference for dense lattice points in the interface, which is a necessary condition for the formation of dense GMS and dense bonds in the low-energy structural units in the interface. However, high-index planes are not excluded from the near-row-matching method, which provides a means for interpreting observations of facets parallel to high-index planes, especially when the matching along the rows is predominantly good [24].

If the resulting matching correspondence in the 2D GMS cluster is one to one, the preferred state is possibly a primary one. To specify the matching correspondence in 3D, one needs to repeat the second step by examining another pair of planes containing the near-matching rows, usually with a small deviation from the OR determined in the previous second step. If a 2D GMS cluster with one-to-one matching correspondence can be found in the additional second step, then a one-to-one lattice correspondence in 3D can be specified using three pairs of non-coplanar, short, good-matching vectors, i.e., one pair of good-matching vectors determined in the first step and one pair of good-matching vectors defined according to the 2D GMS clusters in the two planes determined in the previous and additional second steps. A representative OR is provided by the result from either second step. Because of the multiple selections of vectors in both steps, the representative rational OR for a primary preferred state is not unique. One can test this method using a conventional fcc/bcc system and find the well-defined Bain matching correspondence and well-known rational ORs in the system.

Similarly, one may also obtain the matching correspondence and associated interfacial geometry by conducting the second step in reciprocal space [25]. In the parallel zone axes defined by the pair of good-matching vectors, one arranges the 2D reciprocal points so that rows in different lattices with similar spacing lie parallel to each other to form an OR that meets the near-matching-row condition. Then, the direction of the parallel rows in reciprocal space defines the interface containing near-matching rows in direct space [26]. This method tends to result in an interface parallel to low-index planes normal to a row of dense reciprocal points. It is also possible for less dense rows (often in a metal solid-solution phase) to align parallel to a row of dense reciprocal points in the other phase (usually in the compound phase) to meet the near-row-matching condition [27]. Compared to the method in direct space, it is straightforward to understand the observed OR, when near row matching is visible in a measured diffraction pattern, since the direction of the near-matching rows is usually normal to a preferred interface. In addition, it is more convenient to conduct the additional second step in the same plane in reciprocal space by a slight change in the OR, and find another pair of planes containing near-matching rows in direct space (i.e., K-S OR and Pitsch OR as demonstrated by Gu and shown in Figure 4 in [25]). Then, the matching correspondence in 3D can be determined in a way similar to the method in direct space. In addition, a matching correspondence in reciprocal space in 2D can also be obtained by relating the nearby reciprocal spots.

The near-matching-row method can also be applied to determine the expression of the measured OR in terms of the proper representative rational OR [25]. Though it is conventional to express the measured OR in terms of low-index vectors of either lattice or both lattices, the expression with a representative rational OR carries an implication of the preferred state. For example, the Pitsch OR [28] and Thompson–Howell (T-H) OR [29] between cementite and austenite can be expressed, respectively, by:

[1 0 0]_C//[5 5 4]_A, [0 1 0]_C//[1 1 0]_A and [0 0 1]_C//[2 2 5]_A and

(2a)

[1 0 0]C//[1 1 8]A, [0 1 0]_C//[1 1 0]_A and [0 0 1]_C//[4 4 1]_A

(2b)

where the subscripts C and A are cementite and austenite, respectively. The representative OR derived from the near-row-matching method maintains the good-matching rational directions of [0 1 0]_C//<1 1 0>_A in the above expression and adds the planes of the secondary preferred state, as follows:

(1 0 1)_C//(1 1 3)_A and [0 1 0]_C//[1 1 0]_A and

(3c)

(1 0 1)_C//(1 1 3)_A and [0 1 0]_C//[1 1 0]_A

(3d)

The above expressions of representative rational ORs provide an intrinsic link between the observed different ORs. Namely, the structures of the preferred state in corresponding habit planes have common periodicity [16]. However, the periodical 3D structural units corresponding to the two ORs are different. The difference in the interfacial energy caused by the different structural units may not be too large for this case, since both ORs have been observed. There are small deviations between the measured ORs and the representative rational ORs. These deviations are due to the further development of the ORs at the growth stage, as will be explained in Section 3.2.2.

The experimental observations indicate a strong tendency to develop the primary preferred state. When this overriding preferred state is possible, one usually does not need to take the candidates of secondary preferred states into consideration. On the other hand, the matching correspondence for a primary preferred state is usually well established for conventional systems, i.e., the Bain correspondence for the fcc/bcc system. One may not need to use the near-row-matching method to search for it. Therefore, the near-row-matching method is mainly applied for identifying potential secondary preferred states and the corresponding representative ORs. Among the various potential secondary preferred states, which one or ones are to be realized? A proper answer requires reliable data on the interfacial energy and knowledge of other factors that may affect OR development. Without sufficient information, one may make an estimation based on some empirical rules. As a rule of thumb, the following features are usually favorable: a dense GMS within a row segment, dense rows, low misfit along the row and between rows, and rows along small reciprocal vectors (i.e., planes of the secondary preferred state are low-index planes). However, these conditions may not be satisfied simultaneously. The above conditions imply that small structural units and low misfit strain are preferred. The primary preferred state corresponds to the smallest structural units, which explains why its selection is always a priority.

2.4. Range of OR for a Matching Correspondence

Once the matching correspondence is specified for a preferred state, the geometry permitting the matching correspondence is confined, but the OR may not be fixed. The preferred state can still be maintained in certain regions of the interface if the OR varies within a limited range. That is why different representative ORs may be associated with one preferred state. The range of the OR allowing a particular preferred state to be sustained depends on the matching correspondence in the structure of the preferred state and the degree of misfit restricted by the lattice parameters of the given system. In principle, the range becomes larger as the coincidence sites in a preferred state become denser. This is analogous to grain boundaries. It is well known that the upper limit of the misorientation angle, Δθ_I, is around 10~15° for fully coherent regions (the primary preferred state) to exist between the dislocations in a small-angle grain boundary [6]. For a large-angle grain boundary to be classified as a so-called CSL boundary (in a secondary preferred state), the minimum deviation, Δθ_II, obeys the Brandon criterion [30], i.e., Δθ_II = Δθ_I/∑^0.5. However, the lattice parameters of the two phases of a given system do not usually permit the exact matching required by a preferred state at any OR. Therefore, the limited range allowing a preferred state to be sustained in a heterophase interface is usually smaller than that in a homophase interface. The range of OR corresponding to a one-to-one matching correspondence is relatively large, with an upper limit of around 10°, and that corresponding to an n-to-m matching correspondence is much smaller, usually less than 2°.

A simple way of estimating the valid range of the OR for a preferred state in a given system is to examine whether the periodic structure in the GMS clusters according to the upper good-matching coefficient can survive after the OR is changed. For a secondary preferred state, if the number of repeated units in the GMS cluster in any direction is close to the lower limit for the periodicity at a representative OR, the range of the OR is very small. It is quite common that the observed OR in a system in a secondary preferred state is close to the representative rational OR. Therefore, specifying the representative OR and identifying the matching correspondence in 2D for a secondary preferred state is a major step for understanding the observed OR in a system in a secondary preferred state. By contrast, in a system of the primary preferred state, the valid range of the OR is large. The matching correspondence alone is usually not sufficient for understanding an observed OR.

2.5. Discussion

2.5.1. Influence of Strain Energy

Thus far, we have mainly focused on the ORs that permit the development of a preferred state in the interface between a nucleus and its matrix, assuming that the preferred state is a low-energy structure. Therefore, the nuclei can have a small value of ∑γdA. Whether those associated with this small ∑γdA can proceed into the growth stage still depends on how much the given driving force, ΔG_v, can exceed the strain energy, ΔG_s, as seen in Equation (1). Generally, the lattice parameters of the two phases in a given system do not allow the exact matching required by the matching correspondence at any OR. The deviation of the positions of the actual lattice points from ideal matching in the GMS cluster at the origin defines a misfit-strain field. This misfit-strain field depends on the lattice parameters, matching correspondence and OR. It is the source of the strain energy. The quantitative association of the strain energy with an OR is a challenging task, since the rotation term is not taken into account when the Green strain tensor is applied, as in the usual case, for the calculation of the strain energy based on Eshelby’s inclusion theory [31]. In addition, the validity of continuum theory for the size of nuclei is also questionable. A number of unsolved problems regarding the strain energy were identified by Aaronson et al. [7]. Proper methods for the calculation of strain energy at the nucleation stage are needed.

While low misfit is favorable, a compromise between low γ and low misfit needs to be made in the selection of the preferred state. It is always possible to reduce the misfit strain by changing the matching correspondence, especially changing from the primary to a secondary preferred state. However, the author knows of no evidence suggesting that a secondary preferred state is favored over the primary when the latter is possible (i.e., a GMS cluster with one-to-one matching is definable). This suggests that the fully coherent low-energy structure has an overriding effect on the selection of the matching correspondence in the interfacial structure, even if the associated misfit strain is large.

When ΔG_v is small, less than the ΔG_s associated with a fully coherent nucleus, coherent nucleation is impossible (Equation (1)). The phase transformation may proceed in various ways: Misfit dislocations or other defects are generated to cancel the strain field. The cancellation of the misfit-strain field by dislocations and the possible change in the OR caused by the dislocations are considered in Section 3 for the growth stage, though the dislocations may assist both nucleation and the growth process. It is also possible that the phase transformation proceeds via heterogeneous nucleation near preexisting interfaces. The effect of a preexisting interface on the OR is discussed in the following section in some detail. In addition, the coherent strain field may interact with an external strain field or the strain field of existing defects, such as dislocations in the matrix phase, to reduce the overall strain energy associated with coherent nuclei. Usually, the attribution of the coherent structure in the interface is not altered by the dislocations or vacancies that assist nucleation. Therefore, the preferred ORs obtained from the defect-free assumption are applicable to the cases when nucleation occurs near or at the dislocations or vacancies. However, one may expect that the existing strain field affects the preference for specific variants of an OR or specific ORs if different OR candidates of similar interfacial energy are available.

The misfit strain in a system of a secondary preferred state is usually smaller than that of the primary preferred state. This is because the magnitudes of the corresponding vectors are larger than, but the magnitude of the associated misfit displacement is similar to, the corresponding values in the primary preferred state. Such a system is special in that multiple ORs are often observed. Typical examples are compound precipitates from metal matrices, such as cementite/austenite (Equation (2)) and cementite/ferrite [32], TiN/Ni [33], and Mg₂Sn/Mg precipitation systems [34]. Corresponding to different ORs, the secondary misfit-strain fields are expected to be different. The interaction of the misfit strain with the environment constraint or existing strain field may lead to different results. It is possible that the strain fields of some defects are favorable for one OR but unfavorable for another; this may cause different ORs to form. It is also possible that the selection of the secondary preferred state (and hence, the representative OR) is affected by the transformation temperature, which determines ΔG_v. When ΔG_v is large, the selection of the preferred state associated with a small γ but large ΔG_s is possible. Otherwise, the selection is associated with a small ΔG_s but larger γ. However, this is only speculation. Far fewer investigations have been conducted into the long-range misfit strain in a system of a secondary preferred state than that in a system of the primary. Further work is needed to examine the effect of misfit strain on OR development at both the nucleation and growth stages.

2.5.2. Influence of Preexisting Interfaces

Real materials usually contain interfaces before the occurrence of a phase transformation. These preexisting interfaces are known to be preferred nucleation sites according to the classical nucleation theory [6]. The preferential nucleation is attributed to the reduction in the total interfacial energy of the nucleus owing to the elimination of a certain area of the preexisting interface. This can effectively reduce ΔG* and hence promote nucleation [6,7]. To further reduce the interfacial energy, a preferred OR tends to develop between the nucleus and at least one of the crystals separated by a preexisting interface. The coexistence of low-energy interfaces in contact with both crystals is not always possible. Major investigations into the effects of preexisting interfaces have focused on the systems of the primary preferred state. Systematic experimental investigations were conducted into the crystallography of ferrite nucleated from different preexisting interfaces by Furuhara and colleagues [35,36,37]. Their results offer inspiration to the present consideration of the effects of the preexisting interfaces.

With the following considerations, we assume that a preferred state can be developed in the interface between the nucleus and one of the two crystals separated by the preexisting interface. The OR is usually measured between the product phase and its matrix crystal, into which the product phase grows. In order to specify the interface between this pair of phases, we denote this interface as the P/M interface. The OR measured from the P/M interface may not be the same as the preferred OR formed solely between the two phases related by the phase transformation. To distinguish ORs with and without the influence of a preexisting interface, we use the term of the intrinsic OR for the preferred OR governed by the formation of a preferred state in the interface between the product phase and its matrix, with a valid range of the OR being implied. For a system characterized by the primary preferred state, the intrinsic OR includes a unique region in the geometric space for the OR. For a system that tends to develop a secondary preferred state, there are probably multiple intrinsic OR regions. Below, we consider the influence of preexisting interfaces on the measured OR in three major situations, corresponding to different combinations of the crystals separated by the preexisting interface.

Firstly, the preexisting interface is a grain boundary of the matrix. The grain-boundary plane with respect to one of the grains may favor the formation of a preferred state in the interface between a nucleus and this grain, called the “mother” grain for convenience. Usually, the orientation of this nucleus does not permit a preferred state to form in the interface contacting the non-“mother” grain, since the misorientations between the grains of the matrix phase are usually random. The disordered interfacial structure of the general grain boundary is probably inherited by the interface between the nucleus and the non-mother grain. This incoherent interface is usually not associated with the misfit-strain field and strain energy. Therefore, the total strain energy associated with a nucleus at a general grain boundary is smaller than that associated with a nucleus within a matrix grain. In this sense, the ΔG* is reduced for nucleation at grain boundaries, not only because of the reduction in the total γ, but also because of an increase in the net driving force, i.e., ΔG_v − ΔG_s in Equation (1).

The OR measured from the P/M interface depends on which grain the product phase is to grow into. As stated earlier, the expansion of the interface with a preferred state is likely associated with the strain energy caused by the misfit strain. Thus, in principle, the product phase can grow into its “mother” grain when the available driving force is large, when the misfit strain is small, or when dislocations are available to accommodate the misfit strain. Otherwise, the nucleus grows into the non-“mother” grain. Then, the observed OR from the P/M interface is usually random, and the morphology is possible equiaxial. By contrast, if the product phase can grow into its “mother” grain, the intrinsic OR becomes the reproducible OR observed from the P/M interface. As expected, the larger the misfit strain is, the more likely the product is to grow into the non-“mother” grain and hence form an equiaxial morphology.

The above argument can account for the observation of distinct morphologies of alpha phase in Ti alloys and ferrite phase in steels. Precipitates nucleated from grain boundaries often yield a Widmanstätten structure associated with a reproducible OR, indicating they grow into the “mother” grain. Such a Widmanstätten structure can form in different Ti alloys with small undercooling [7]. Ferrite nucleated from grain boundaries can also form a Widmanstätten structure in steels only when the undercooling is large enough to provide sufficient driving force [7]. If the undercooling is small, the ferrite tends to grow into the non-“mother” grain, leading to the formation of the equiaxial ferrite at grain boundaries. The reason for the ease of obtaining an equiaxial morphology in steels compared with that in Ti alloys is likely due to the significantly different misfit strains: the misfit strain for Ti alloys is much smaller than that for steels (as reflected by the difference in the spacing of the dislocations in the habit planes of the Widmanstätten plates, i.e., ~10 nm for Ti alloys vs. ~2 nm for steels). This confirms the expectations of Aaronson et al. to explain the comparatively large undercooling needed for Widmanstätten ferrite [7].

We move on to the other two types of preexisting interfaces, which are heterophase interfaces. The product phase must grow into the only matrix phase. If the third crystal, besides the growing product phase and the matrix, is the same as the product phase, the preexisting interface is called a domestic interface for convenience—otherwise, a foreign interface. When nucleation occurs at a domestic interface, the same preferred state tends to be developed between the nucleus and its matrix. In this case, the previously formed grain of the product phase is usually associated with a misfit-strain field. A particular variant of the intrinsic OR then forms so that both the interfacial energy and strain energy can be reduced. This is a well-known phenomenon of variant selection [35]. The results of a recent simulation on an fcc/bcc system [38] showed that the reduction in strain energy plays a dominant role in the variant selection. The formation of low-energy grain boundaries between the early and new grains of the product phase is also favored in the detailed variant selection.

The same principle underlying the above discussions is applicable to the cases in which nucleation occurs at a foreign interface. When there is no preferred OR between the third phase and the matrix, the results are similar to those obtained from the case of grain boundaries. Namely, if the interface between the nucleus and matrix has an overwhelming influence, an intrinsic OR forms between them, with a variant probably affected by the preexisting interfaces. If the third phase is added intentionally to prompt heterogeneous nucleation, the governing preferred state often forms in the interface between the third phase and the nucleus. When no preferred OR exists between the third crystal and the matrix, the OR observed from the P/M interface is not reproducible. This situation normally occurs when the third crystal is among the inclusions formed during solidification. It is also possible that the inclusion is located at the grain boundary. Then, the product phase nucleated at this inclusion grows into both grains, and the product phase does not have a preference for ORs with respect to both grains. If the third crystal is precipitated earlier from the same matrix, there is usually a preferred OR between them. There is then a specific OR between the product and matrix phase due to an orientation transmission, i.e., from the OR, between the matrix and third phase and between the third and product phases. This OR is usually different from the intrinsic OR, and it may be reproducible only to a limited extent.

2.5.3. Influence of Composition

As stated earlier, the interfacial energy consists of structural and compositional components [2]. The preferred states have been searched only according to the periodicity of the structure, as reflected in the GMS clusters, irrespective of the composition of the phases. The composition appears to have little effect if the primary preferred state is selected. This can be verified by the observations of similar reproducible ORs between the same types of crystals in different alloys. For example, the observed ORs between the hcp and bcc phases are close to the Burgers OR in almost all alloys consisting of these phases. It is conceivable that the primary preferred state starts from the nucleation stage, since coherent structures can hold between dislocations in the habit planes in these alloys, such as Zr-Nb [39] and Ti-Cr alloys [40]. Similarly, the well-known Bain (one-to-one matching) correspondence is applicable to different alloys consisting of fcc/bcc phases, such as steels [41], Cr-Cu [12], and brass [42].

However, the compositional component of the interfacial energy is expected to have a stronger effect on systems in a secondary preferred state, if one makes an analogy to the structures of grain boundaries. The structural units in singular large-angle grain boundaries (secondary preferred state) are usually less compact than those in small-angle grain boundaries (the primary preferred state) [43]. Though little is known about the details of the atomic structure of the repeated structural units in a secondary preferred state in interphase interfaces, these structural units are likely to be less compact than those in the primary preferred state. One structure may favor occupation by atoms of particular elements over others. Thus, it is possible that the selection of the secondary preferred state is affected by the segregation of the atoms of some elements in interfaces. This possibility opens an opportunity to tailor the preferred state and associated morphology of precipitates by micro-alloying design. Much is to be learned about the structure of structural units before such an application of a knowledge-based design.

3. Growth Stage

An OR initiated from the nucleation stage possibly changes at the growth stage and becomes almost fixed at the later stage of growth. Imagine that if there is no misfit in 3D for a system in the primary preferred state, or in the planes of a secondary preferred state, the representative rational OR is maintained at the growth stage so as to keep the interface misfit-free (or with a negligible misfit). Therefore, the central reason for the adjustment of the OR at the growth stage is the interfacial misfit. Unless the misfit strain is negligibly small, misfit dislocations will be generated sooner or later to cancel the misfit strain and hence reduce the strain energy, provided that the temperature is sufficiently high for the generation of dislocations.

While the conventional definition of nucleation and growth [6] is followed, the influence of misfit dislocations on the evolution of the OR is considered at the growth stage. This does not mean dividing nucleation and growth stages according to coherency loss. A product phase can grow either with or without dislocations. A preferred state must initiate at the nucleation stage, but whether misfit dislocations are needed at the nucleation stage in a given system is unclear. It probably makes no difference for understanding the final reproducible OR when the role of misfit dislocations is treated at the growth stage. In this study, the main results derived from the nucleation stage are the matching correspondence in a preferred state and a range of ORs corresponding to the matching correspondence. We assume that the OR at the growth stage starts from a representative rational OR initiated at the nucleation stage, and that the corresponding preferred state and matching correspondence are sustained locally in interfaces. Only the two phases related by the phase transformation are taken into consideration, but the same line of thought can be applied to the cases affected by a preexisting interface.

For a preferred state to be sustained, the change in the OR at the growth stage is limited within the valid OR range for the preferred state. Though the range for a secondary preferred state is small, that for the primary preferred state is considerably large (i.e., ~10°). In principle, given any OR in this range, one can calculate the dislocation structure in an interface of a known orientation based on the O-lattice theory [17]. Conversely, the existence of infinite possible interfacial dislocation structures implies numerous selections of ORs, each of which could permit the preferred state to be sustained in the corresponding semicoherent interface. Then, what is the OR observed?

A reproducible OR must be associated with reproducible dislocation structures. Such a preferred dislocation structure must be stable, and the orientation of the interface containing the dislocation structure must also be stable. Namely, it has a preferred orientation, seen as a faceted plane. Therefore, the reproducible OR is usually associated with preferred interfaces, as confirmed by accumulated observations. The preferred structure in a faceted interface is the key feature for rationalizing a reproducible OR. The features of faceted interfaces have been summarized previously [19], with some results being briefly reviewed in Section 4.

One interface preferred in the given transformation condition is sufficient to limit the OR. This preferred interface either is free of dislocations or contains periodic dislocations. Whether the OR changes from the representative rational OR initiated at the nucleation stage depends on whether the formation of a preferred structure causes the change. This is related to the types of initial OR. If the misfit-strain field is isotropic in the initial OR, the initial OR is an invariant OR. Usually, if the growth starts from an invariant OR, a preferred interfacial structure, with or without dislocations, can form with the OR inherited from the nucleation stage, as will be further explained in Section 4. Therefore, such an invariant OR will become the observed reproducible OR after the misfit strain is accommodated by interfacial dislocations. It is more challenging to identify and understand what OR will be stabilized as it is developed from a variant OR initiated at the nucleation stage. This is the major concern addressed in this section.

The natural selection of the Burgers vectors of the dislocations is a critical issue for understanding the preferred dislocation structure in a given system. Two principles must be followed. Firstly, the selection of a Burgers vector must be in accord with the preferred state. A Burgers vector of an interfacial dislocation defines a relative displacement between the specific matching correspondences at the adjacent regions separated by the dislocation. It must ensure the same structure of the preferred state repeats in the two regions. To maintain one-to-one matching correspondence in regions, the Burgers vector must be a lattice translation vector of either lattice. To ensure the pattern of the CSL that represents a secondary preferred state in the regions, the Burgers vector must be a lattice translation vector of the DSCL (DSCL stands for the complete pattern-shift lattice) according to Bollmann, who has provided details of the construction of CSLs and DSCLs and the relationship between them in a well-known book [15]. Secondly, a Burgers vector must be small, as is energetically favored [5]. Under this principle, the Burgers vectors of the dislocations separating coherent regions are common to those of dislocations within either phase.

Though the principles governing the evolution of the OR are the same for systems in either a primary or secondary preferred state, the details are quite different, so they are considered separately below. Examples are provided, but the detailed model set up and calculation methods for these examples will not be reviewed. Readers are referred to the original references cited for the details.

3.1. Primary Preferred State

In this section, coherent growth is considered first. This type of growth is possible only when misfit is negligibly small, or when the size of the new phase is very small. The product phase considered in the present approach is a single crystal, so only the interfacial misfit dislocations are taken into consideration for the misfit accommodation. Other defects, such as twins or stacking faults, in martensite can also accommodate the misfit strain, but these are internal defects of the product phase. Provided with a limited set of known Burgers vectors in either phase, there are still many questions to be answered, such as, will the dislocations with all these candidate Burgers vectors be presented in an interface? How are dislocations generated? Will the dislocations fully accommodate the misfit strain? If not, which Burgers vector(s) will become the Burgers vector(s) of the interfacial dislocations generated during a phase transformation in a given condition? How much misfit strain is relaxed in a given transformation condition? What is the effect of the dislocation generation order and the residual long-range misfit strain on the OR development? The implication of these questions is that the OR developed at the growth stage is closely related to the dynamic picture of dislocation generation. While the effect of this process on the evolution of ORs remains unclear, great efforts have been made to rationalize the observed ORs and orientations of preferred semicoherent interfaces after growth stops. Various models have been proposed to relate interfacial structures to ORs in different systems. Complete answers to the above questions are beyond the scope of the current results, but a best attempt is made below to offer some answers based on progress in experimental, theoretical and simulation studies.

3.1.1. Coherent Growth

There are two cases in coherent growth. In one case, which needs special lattice parameters, matching is attainable without causing any distortion of the two phases. The one-to-one matching positions define an invariant OR initiated from the nucleation stage. This is kept at the growth stage to preserve a good-matching interfacial structure. A typical example is the coherent γ’ precipitates in a superalloy [44].

In another case, which is more common, a variant OR is initiated from the nucleation stage. Coherent growth may be possible if the misfit strain is small or the size of the product phase is limited. As stated earlier, it is impossible to maintain different pairs of planes parallel with a single OR without the distortion of both phases. In order to examine the possible coherent growth in such a complicated case, a pseudo fcc-to-bcc transformation was investigated by an atomic simulation (with a reduced misfit-strain field, since otherwise, coherent growth is impossible) [45]. As guided by a previous simulation [46], the growth starts from the Nishiyama-Wassermann (N-W) OR ((1 1 1)//(0 1 1)_α and [1 1 0]_γ//[1 0 0]_α, where the subscripts γ and α stand for austenite and ferrite, respectively). The final shape of ferrite is an elongated platelet, which is presumably in equilibrium since this shape is quite stable and reproducible, independent of the initial shapes. It has a broad face near (3 3 5) and an elongated direction near [1 1 1]_γ. The shape together with the crystallographic descriptions can be interpreted by the minimization of the strain energy, calculated using Eshelby’s inclusion theory. This result indicates the dominant role of the strain energy in the evolution of the shape during the coherent growth of the product phase. The broad face and elongated direction of the platelet also agree with the broad face and elongated direction of a special ellipsoid, whose surface is defined by equal Burgers vector content (equivalent to the magnitude of misfit displacement). This ellipsoid can be calculated with a simple algorithm [47] extended from the Burgers vector content method [48], with the input of the misfit-deformation matrix A (A can be determined with the input of lattice parameters, a matching correspondence, and a given OR). The above agreement means that the broad face and elongated direction of the coherent platelet are the best-matching plane and direction, indicating a strong effect of anisotropic interfacial misfit on the shape after coherent growth.

Theoretically, the shape of a coherent particle is also affected by the anisotropic elastic constants of the two phases, as the product phase tends to grow into a soft dislocation. In the simulation result [46], this effect of crystal anisotropy cannot be clearly distinguished, though the anisotropy ratio of the system is around two, considerably larger than one, the isotropy ratio. For simplicity, in the following consideration, we focus on the effect of the misfit distribution on the development of the phase-transformation crystallography. However, the possible influence of anisotropic elastic constants should be taken into consideration, especially when the influence is obvious and the prediction based on misfit analysis does not agree with the observations.

In the simulation results mentioned above [45], coherent growth did not lead to detectable change in the OR. In principle, (1 1 1) and (0 1 1)_α can remain parallel only when the parallelism is held by these two planes being contacted in a large step-free facet of the coherent particle. However, the actual broad interface (~(3 3 5)) contains terraces parallel to (1 1 1)_γ and (0 1 1)_α separated by steps, so it contains the best-matching direction (~[1 1 1]_γ), which is significantly inclined with respect to (1 1 1)_γ. This stepped structure is equivalent to that described by the structural-ledge model [13,18]. Because the interplanar spacings of (1 1 1) and (0 1 1)_α, i.e., the step heights, are usually different, the contact of (1 1 1)_γ and (0 1 1)_α in every terrace causes a torque to rotate the lattices with respect to each other. When the particle of the product phase is small, as at the early stage of growth, it is probably free to rotate under the effect of the torque until the steps can meet edge-to-edge. If the misfit in the height is small, the rotation caused by the torque is also very small. Even if it exists, the OR may appear unchanged after the elongated shape is formed, as in the simulation result [45]. For the same reason, such a small rotation may also often be blurred by the experimental uncertainty.

It is more convenient to determine the necessary rotations in terms of a general invariant-line strain, which is a direction free from misfit. After a proper rotation, the best-matching direction becomes an invariant line. Phase-transformation crystallography characterized by an invariant-line strain is very common in fcc/bcc and hcp/bcc systems, as shown by numerous experimental results [49,50,51,52]. While the invariant line plays an important role in the development of the ORs, this condition does not fully constrain the OR. A systematic way of examining the ORs corresponding to the invariant-line strain is analyzing the misfit-deformation matrix A. Any matrix A can be decomposed into a pure deformation and a rotation. The pure deformation is decided by the lattice parameters of the two phases and the matching correspondence, so it is fixed corresponding to each preferred state. The rotation term is defined by the OR, such that each A corresponds to a specific OR. A pure deformation is characterized by the principal deformation λ_i (i = 1, 2, 3). For the details of the determination of λ_i, the readers are referred to a book by Christian [5]. He showed that an invariant line is possible if one λ_i > 1 and another λ_i < 1. When the above condition is met, there is a cone of unextended lines, defined by directions of unchanging length after the principal deformations. By a suitable rotation, any line in the unextended cone may be rotated to its original position to become an invariant line [5]. Therefore, there are numerous ORs corresponding to the various directions of the invariant lines. A small rotation around each invariant line also yields a degree of freedom in an OR, with all resulting ORs satisfying the geometry needed for the same invariant line. Among the three degrees of freedom in the OR, the invariant-line condition only confines one degree. In the case of an invariant-line strain, the surface defined by equal Burgers vector content is a cylinder instead of an ellipsoid. The area of the cross-section of the cylinder indicates the misfit in the direction normal to the invariant line. It was found that in an fcc/bcc system, the same shape of the largest cross-section area could be obtained when any line in the unextended cone was directly rotated to its original position [53]. A further rotation around the invariant line reduces the cross-section area [53], implying an increase in the overall misfit. In this sense, any OR corresponding to a direct rotation for an invariant line to form, without any further rotation, has an equal opportunity to become the preferred one.

Multiple directions of invariant lines have been confirmed by experimental results provided by Dahmen and Westmacott [54], who performed a pioneering study on the role of the invariant line in phase-transformation crystallography. In their study of Cr precipitates in a Cu-Cr alloy, they found needle-shaped Cr precipitates, with the needles (whose directions are presumably defined by invariant lines) distributed rather randomly in the unextended cones when the precipitates were coherent. However, they did not report the ORs associated with the coherent precipitates in different directions, probably because these precipitates are too fine to measure the ORs in the available experimental conditions. In a theory by Dahmen and Westmacott (DW theory), the invariant lines are developed at the nucleation stage, but only those that lose coherency can grow. The present approach includes coherent growth at the growth stage, so coherency loss is not regarded as the dividing feature between nucleation and growth stages. However, this discrepancy does not cause a conflict in the understanding of the reproducible OR after coherency loss and semicoherent growth, considered in the next section.

3.1.2. Coherency Loss

The relaxation of the misfit strain is closely related to the generation of the dislocations. In general, at least three sets of dislocations with non-coplanar Burgers vectors are needed to fully accommodate the misfit strain in 3D. The concurrent generation of all necessary dislocations is usually impossible. It is also possible that some misfit strain may be tolerated at a certain growth stage. It is desirable to reveal the evolution of the OR in the process of misfit-strain relaxation with the steps of dislocation generation. Unfortunately, the experimental details about this process are very limited.

A recent atomic simulation of the coherency loss of a Cr precipitate in a Cu matrix provides some enlightening hints about the role of the dislocations in the change in the OR [9,46]. The simulation results show that a coherent bcc precipitate develops a near-N-W OR with a shape characterized by a major facet parallel to (1 1 1)_f and (0 1 1)_b, where the subscripts f and b denote fcc and bcc lattices, respectively. Note that such a coherent, atomically flat habit plane ensures the parallelism of a pair of the most closely packed planes in both phases. This can be considered as the representative rational OR for the variant OR at the nucleation stage. At the beginning of coherency loss, discontinuous changes in the OR are obvious in response to the generation of each major dislocation loop, which is most prominent when the second loop is generated. The Burgers vector of the dislocation is [1 0 1]_f/2|[1 1 1]_b/2, and the loop plane is approximately defined by (1 0 1)_f|(1 1 2)_b. The result indicates that the evolution of the OR of a semicoherent precipitate is governed by the major dislocation loops, though another set of loops also exists to accommodate the misfit. The Burgers vector of each dislocation loop lies in the corresponding loop plane for both sets of dislocations, implying that the expansion of the loops in the growth process is in accord with the slip process of the dislocations. The shape of the precipitate after the final step of the simulation is elongated with the long axis close to the invariant line, and with a major facet containing a set of [1 0 1]_f/2|[1 1 1]_b/2 dislocations. As the precipitate grows, the orientation of the major facet changes towards the O-line interface with the minimum interfacial energy, and the OR changes towards the OR that provides the geometry needed for the O-line interface, in agreement with the O-line criterion explained below.

3.1.3. Single Set of Dislocations

The dislocations formed in the coherency-loss process may not fully accommodate the total misfit strain, since there are not enough sources for misfit dislocations. However, to reduce the strain energy, at least one set of dislocation loops must be generated. Then, the residual misfit strain remains in the form of a long-range elastic strain. Among the candidates of Burgers vectors, which one is selected to be the Burgers vector for the dislocation loops that are first generated? What is the reason behind the selection? What is the OR caused by the formation of the dislocation loops? Different models related to these questions will be reviewed below.

In the study of Cr precipitates in a Cu-Cr alloy, Dahmen and Westmacott [54] found that the needles of Cr precipitates converge to certain directions after the loss of coherency. They proposed a theory (DW theory) to explain the observation. In their theory, the total transformation strain (A), equivalent to the misfit deformation, is decomposed into a simple shear (P) and a pure deformation (S), i.e., A = PS. The simple shear is cancelled by one set of the dislocation loops formed during the growth of the precipitate, and the remaining deformation is accommodated elastically. The convergence of the invariant lines is due to the unique shear system of the dislocations, {111} planes defined in an fcc matrix, in which the invariant line must lie. Their theoretical results are in good agreement with the observed the directions of the semicoherent needles. However, as they admitted, not every invariant-line strain can be decomposed into PS. On the other hand, a combination of PS does not always yield an exact invariant-line strain.

The above decomposition is different from the well-known decomposition of A in the phenomenological theory of martensitic crystallography (PTMC) [55], in which an invariant-line strain is known as the key feature. In the PTMC, A comprises a macroscopic invariant plane strain (P₁) and a lattice invariant deformation (P₂) defined by gliding a set of defects, such that A = P₁P₂. Because both P₁ and P₂ are invariant plane strains, A must be an invariant-line strain. While the glissile defects include twins and stacking faults in addition to the dislocations for a martensitic phase transformation, the shear effect can be equivalent mathematically to a set of dislocation loops. The misfit strain in the habit plane must be fully cancelled by the defects, so that it is the macroscopic invariant plane [55]. The habit-plane normal and the corresponding OR can be solved from the PTMC based on the assumed vectors to specify the lattice invariant deformation. In particular, the invariant line must lie in the slip plane of the lattice invariant deformation, which is the same as that required by the DW theory [54].

The O-line criterion [47] is another constraint narrowing the selection of the invariant line. The O-lines are periodic linear positions of zero misfit along the invariant line. They are called O-lines because they are the line-shaped O-elements defined in the O-lattice theory [15,17]. It is similar to the PTMC in that a single set of dislocations between the O-lines fully accommodate the misfit in the habit plane. Such an interface is called an O-line interface for convenience. Any invariant line in the unextended cone may become the direction of the O-lines by a suitable rotation. By contrast, the invariant line in the reciprocal space is not free in the unextended cone in reciprocal space, because it must be normal to the Burgers vector of the dislocations [56]. The O-line criterion is equivalent to the application of one constraint in the lattice invariant shear in the PTMC [57], but without using the other constraint, i.e., the dislocations must lie in the slip plane. Because of the common constraint, the habit plane predicted by the PTMC is covered by the O-line criterion. In this sense, the O-line criterion is more general. However, the O-line criterion does not fix the OR. It only restricts two degrees of freedom in the OR.

In addition to the one degree of freedom in the OR along a constrained route for the O-line interfaces of a given Burgers vector, there are multiple choices of Burgers vectors for the dislocations. When the corresponding Burgers vectors are from the same pair of families of vectors in the two lattices, the determined results may be crystallographically equivalent variants. This will virtually reduce the choices of the Burgers vectors. For example, there are only two types of Burgers vectors in an fcc/bcc system [58]. Methods for calculating the ORs corresponding to all O-lines for possible Burgers vectors in fcc/bcc and hcp/bcc systems have been derived [59,60] together with a free software called PTClab [61].

A molecular dynamic study of interface migration in an fcc/bcc system showed that the dislocations in an O-line interface can glide in their slip plane (either rational or irrational orientation), and the migration is associated with a shear between two lattices [62]. This motion is equivalent to the expansion of the set of dislocation loops in their slip planes. The shear displacement can be determined either according to the displacement (Δb) necessary for the O-line interface to move [63], or according to the PTMC [55]. The long-range strain may be sustained if the driving force is sufficient to surpass the strain energy due to the residual misfit, regardless of whether the phase transformation is diffusional or diffusionless. This situation is common to conditions in both PTMC [55] and the DW theory [54], in which a part of the misfit strain remains in the form of elastic strain. Since the O-line interface is free from a long-range misfit strain, the residual strain field is always an invariant plane strain. Following the PTMC, the decomposition of A can be expressed by A = P_rP_h. The misfit in the habit plane is cancelled fully by the dislocation loops (P_h), and the rest (P_r) remains a long-range invariant plane strain. The strain energy is expected to increase monotonically with the magnitude of the strain (m_r) in P_r.

Dai et al. [64] conducted a systematic investigation of varying m_r with the loop planes under the condition that the habit plane was an O-line interface in an fcc/bcc system, with [1 1 1]_b/2|[1 0 1]_f/2 as the Burgers vector of the dislocations. According to the calculation results, the misfit strain in the simulation system was accommodated most efficiently by a (1 1 2)_b [1 1 1]_b/2 or, correspondingly, (1 0 1)_f[1 0 1]_f/2 shear system. In other words, the shear deformation by these dislocation loops was closest to A. Therefore, under the condition of minimum residual strain, the optimum OR and the orientation of the habit plane can be determined among various candidate shear planes.

The above approach shares some similarities with the DW theory [54] and PTMC [55]. Since the residual strain is minimized, the total transformation strain A may be approximated by a shear deformation produced by the gliding of the dislocations. This result agrees with the requirement in the DW theory, i.e., the nuclei can grow and lose coherency, as they have a “shear component in the direction of a Burgers vector” [54]. However, the residual elastic strain is different from a pure deformation, assumed in the DW theory. Instead, it is an invariant plane strain, common to the condition in the PTMC [55]. While the shear system in the PTMC is a unique input, the above approach extends the inputs to numerous shear planes and yields an output of the optimum shear plane. This extension may shed some light for understanding the cases when only one set of dislocations can be generated in the interface and when the strain energy due to the residual strain also plays a role in the determination of the OR.

3.1.4. Multiple Set of Dislocations

When the transformation temperature is high, it is possible that all the needed dislocations can be generated so the overall misfit can be fully accommodated by interfacial dislocations. In this condition, the dislocation structure in an interface can be determined according to the O-lattice theory [15,17] and its extensions, which provide further calculation formulas [65,66], with the input of the interface orientation, the misfit deformation matrix, and candidate Burgers vectors. In this calculation, the OR is an input buried in the misfit-deformation matrix (A), but for the investigation of the development of the OR at the growth stage, the OR is a variable. The reproducible OR is closely related to the shape of the product phase after growth. Experimental results indicate that if the generation of different sets of dislocations is possible, the product phase is often surrounded by several faceted interfaces. This is a signature of the existence of multiple sets of dislocations, in contrast to the tapered edge of a habit plane, when only a single set of dislocations is available, in the habit plane. In general, the reproducible OR provides the geometry condition for at least one of the faceted interfaces to form a stable interfacial structure. Consequently, the OR also becomes stable and reproducible. Various possible stable interfacial structures are considered in Section 4.1 in terms of singularity in interfacial structures, presumably associated with local energy minima.

Below, the development of the ORs at the growth stage is considered according to whether or not the representative rational OR initiated from the nucleation process is to be altered.

Rational OR

A representative rational OR initiated from the nucleation stage is governed by matching in the preferred state. If the OR belongs to an invariant OR, the misfit-strain field is usually isotropic. A rotation away from this rational OR will usually lead to an increase in the interfacial misfit, whether the interface is coherent or semicoherent. Therefore, an invariant OR will usually remain unchanged after the generation of misfit dislocations. The corresponding representative rational OR will be observed as the reproducible OR. If the OR initiated from the nucleation stage belongs to a variant OR, the OR after semicoherent growth can be either rational or irrational. The result depends on the governing interface developed preferentially at the growth stage in a given phase-transformation condition, which varies case by case. A stable dislocation structure can always form in a flat interface parallel to a pair of low-index planes containing two or three Burgers vectors in the two phases. The observation of such an interface is usually accompanied by a reproducible OR defined by a representative rational OR corresponding to the parallelism of this pair of planes. Among several representative rational ORs, the selection of a specific OR may be understood based on a comparison of the misfit distributions in the flat interfaces with different rational ORs.

Irrational OR

Compared with rational reproducible ORs, irrational reproducible ORs are more challenging, because it may be unclear why a particular rotation is preferred between two low-index directions or planes. In such a case, the OR is altered from the initial OR, described by a representative rational OR, during the growth to provide the geometry for the governing interface to contain an optimum interfacial structure. As stated in Section 3.1.2 and Section 3.1.3, rotation away from a rational OR usually results from the formation of a better-matching direction, i.e., an invariant line. The dislocation structure consisting of a single set of dislocations along the invariant line is a stable dislocation structure, as manifested by the frequent observations from the habit plane of precipitates [3]. This invariant line is usually in an irrational direction. For a preferred interface to contain this direction of zero misfit, the interface must contain steps, with the terrace planes defined by the low-index planes of a matching pair. The step heights defined in the two phases are usually different. To ensure zero misfit along the invariant line inclined to the terrace planes, a rotation is necessary between the terrace planes defined in different phases.

When the habit plane is such an O-line interface, containing a set of parallel dislocations, the other facets usually contain two sets of parallel dislocations, because the O-lines are only solvable in one interface in a normal system. However, only the structure in the habit plane is taken into consideration for the interpretation of the reproducible OR. As mentioned earlier, there are many ORs that can meet the O-line condition. To limit the OR for the O-line interface, a major restriction is based on the principle of minimizing the interfacial energy of the habit plane. The interfacial energy is assumed to decrease with the dislocation spacing, so the maximum dislocation spacing was previously selected as the constraint to limit the remaining one degree of freedom in the OR in the O-line condition. This constraint is supported by the observations of the OR, the habit-plane normal and dislocation structures in alloys in hcp/bcc systems, such as a Zr-Nb alloy [52] and Ti-Cr alloy [51]. Nevertheless, it failed to explain the frequently observed near-K-S OR [12,49,67], since the dislocation spacing in an O-line interface with a near-N-W OR is considerably larger than that with a near-K-S OR (i.e., ~2.5 vs. ~1 nm [68], in contrast to ~10 nm in an hcp/bcc alloy [51]). The assumed reverse relationship between the dislocation spacing and interfacial energy possibly becomes invalid when the dislocation spacing is too small, since the dislocation core energy now has a stronger effect on the interfacial energy. According to a calculation of the interfacial energy of all O-line interfaces with both types of Burgers vectors in an fcc/bcc system, the O-line interface with a near-K-S OR has proved to be associated with the minimum interfacial energy [64].

The above analysis is based on a consideration of misfit in 3D. There exist a number of 2D models in studies of irrational ORs related to the invariant-line condition. The 2D models can be demonstrated with figures in 2D, which is much more straightforward than a 3D approach that needs a matrix calculation. The OR in a 2D model usually starts from a rational OR in which a pair of closely packed planes in different phases parallel to each other and a pair of related Burgers vectors are parallel to each other, such as the K-S OR in an fcc/bcc system, which can be regarded as a representative rational OR initiated from nucleation. If the planes remain parallel, it is possible to form an invariant line in the planes by a proper rotation, with an angle that can be solved analytically, as derived by Dahmen [69]. However, this OR may not meet the O-line condition. If two Burgers vectors remain parallel, a rotation around them will also yield an invariant line [70,71]. Since this is a 2D model to solve a 3D problem, the actual invariant line may not lie in the plane for the 2D calculation, unless planes normal to the parallel Burgers vectors are also low-index planes containing vectors related by the matching correspondence [72]. It is more convenient to perform a 2D calculation in a reciprocal lattice in the zone axes defined by the parallel Burgers vectors to determine the required OR for the invariant line, similar to Dahmen’s derivation in direct space [69], and the invariant-line direction can also be determined analytically [72]. The interface containing this invariant line and the Burgers vector is an O-line interface. This can be proved according to the O-line properties [47]: the misfit displacement of any vector in the interface defined in one lattice is parallel to the Burgers vector defined in the other lattice.

Because the resulting invariant line is inclined to the nearly parallel, closely packed planes after the small rotation, the O-line interface contains steps with the terraces along the parallel planes. The step structure has been treated as a prominent feature for rationalizing the irrational orientation of the stepped interface and associated OR in different 2D models. These include the early lath martensite model in terms of the cancellation of the misfit displacement in the terraces and steps, proposed more than half a century ago by Frank [73]; the edge-to-edge model, which emphasizes the edge-to-edge matching of the steps [74]; and the more recent topological model [75], in which the role of the steps (called disconnections) is particularly addressed with an analysis similar to that for the Frank model but in terms of a more-complicated cancellation of the misfit strain [75,76]. (A detailed comparison of the steps in an O-line interface with a description with disconnection can be found in [77].) While the existence of these types of special O-line interfaces have been confirmed experimentally, e.g., [78], these interfaces belong to a special case. The observed O-line interfaces do not always contain the parallel Burgers vectors of the interfacial dislocations, especially in an hcp/bcc system [51,79].

Finally, it is worth mentioning another type of special constraint on the OR, which also demonstrates a great tendency to form an invariant line, and its strong effect on the development of reproducible ORs. When the product phase forms near a surface or in a thin foil such as in a TEM sample, the product phase tends to grow along an invariant line, lying in the surface. This result was reported early by Dahmen and Westmacott [54], and was confirmed repeatedly in investigations by the author’s group [80,81]. The constraint of the direction of the invariant line does not fix the OR, but with the O-line condition, the OR is fixed. Some O-line interfaces are indeed observed from precipitates on the surface [81], but the selection of other ORs might be affected by different factors [80]. In general, the invariant-line directions together with the ORs vary widely with the random surface of the grains of the parent phase. Consequently, the OR is reproducible only within a particular grain.

3.1.5. Discussion

While the O-line criterion has been validated by accumulating experimental observations from fcc/bcc or hcp/bcc systems, the constraint for fixing the OR for the O-lines remains uncertain, as it often requires guidance from experimental observations. To further explore the affecting factors, Dai [9] conducted a systematic investigation of the ORs, invariant-line directions and equilibrium cross sections of precipitates by varying the types of shear loops, in the conditions of the misfit strain being fully accommodated by misfit dislocations and one facet containing the O-lines. The ORs corresponding to the O-line interfaces with the minimum interfacial energies or minimum residual strains based on the single set of loops were determined. However, no OR could meet both minimum conditions. It is possible that the selection of the Burgers vector of the dislocations is governed by the minimum interfacial energy, and the shear system is likely governed by the minimization of the strain energy, as suggested in the simulation result [9].

Which condition has a dominant effect on the development of the OR depends on the specific phase-transformation system and phase-transformation condition. The selection of the Burgers vector of the dislocation loop and loop plane may also be affected by kinetic factors, such as the ease of dislocation nucleation, dislocation mobility, which will affect the rate of energy dissipation in the transformation. This aspect is closely related to the transformation temperature, which may alter the dislocation structure corresponding to the optimum energy dissipation during a phase transformation, i.e., via providing the driving force to surpass the strain energy and the thermal activation for assisting the generation and migration of dislocations. This relationship may account for the change in OR and morphology with the transformation temperature in some systems. Being glissile is an optimum condition based on interface kinetics, known as the key condition in the PTMC. Sufficient driving force provided by large undercooling is required for martensitic transformation in steels. Much less is known about the temperature effect on the phase-transformation crystallography. Further investigations of this effect are urgently needed.

The above considerations for the development of the ORs at both nucleation and growth stages in systems in the primary preferred state are mainly based on observations of metallic materials. The effects of the composition and types of bonds have been neglected. Possible segregation in the dislocation cores may affect the dislocation energy, their mobility, and hence, the preference of the dislocations in the interfaces. However, little is known about this aspect.

On the other hand, the compositional component is known to have a stronger weight in the interfacial energy in a ceramic system. This component is more sensitive to the interface plane, and the preferred interface is often parallel to a low-index plane of the ceramic phase [33]. In a system consisting of ceramic phases, good matching still plays a role in the selection of the contacted planes for the preferred interface [82]. In this case, it is also appropriate to treat the preferred state in 2D when the particular contact planes are preferred to serve as the interface, similar to a secondary preferred state in 2D. Regular up-and-down steps may be added to improve the matching between the preferred structural units in terraces, as observed in the interface between Ti(C,N) precipitates and TiB₂ matrix [82]. In the meantime, the OR remains rational.

3.2. Secondary Preferred State

Far fewer investigations have been performed into the interphase interfaces in secondary preferred states compared with those in the primary preferred state. In a secondary preferred state system, the reproducible ORs are often expressed with high-index vectors, which may look odd to those who are familiar with the system in the primary state. Examples from experimental results will be provided in this section to illustrate the high-index features and applications of the present approach. Similar to the systems in the primary preferred state, the development of the OR at the growth stage is closely related to the final shape of the product phase. In contrast to the interface in the primary preferred state, in which the primary preferred state exists in the interface surrounding the product phase, the secondary preferred state developed at the nucleation stage only lies in one portion of the interface. This portion of the interface is parallel to the planes of a secondary preferred state, in which a rational plane from each phase contacts each other in the interface. At the growth stage, the secondary preferred state is preserved at least locally in one interface. This local 2D periodic structure greatly limits the range of the OR that can be altered at the growth stage. Therefore, the range of the adjustable OR with respect to the representative rational OR is very small at the growth stage, usually less than around 2°. Therefore, the ORs observed after the growth stage can often be approximated as the representative rational OR associated with a secondary preferred state. Likewise, one may suggest the representative rational OR according to the observed OR, and rationalize the OR mainly according to the associated secondary preferred state.

It is possible for the crystallographic equivalent or different secondary preferred state to coexist in different facets, if the OR permits the coexistence. However, one preferred state is sufficient to fix the OR. When the secondary preferred states in facets are symmetrically equivalent, any one of these facets can be used for the study of the OR at the growth stage. In a more general case, it is reasonable to select the secondary preferred state lying in a major step-free facet as the dominant preferred state as the reference for further analysis. The area of this major facet is usually relatively large, but it may not always be the largest one.

In the following analyses, the OR is considered to start from a known representative rational OR corresponding to a secondary preferred state developed from the nucleation stage, which can be either guided from observations or predicted with the near-row-matching method. The adjustment of the OR is attributed to the optimum accommodation of the misfit with respect to the secondary preferred state. While the details vary case by case, experimental data have demonstrated general tendencies, which will be summarized below.

3.2.1. Coherent Growth

When the lattice parameters permit an exact CSL in 2D, there is no secondary misfit. The coincidence-coherent structure can then extend in the interface along the planes of the secondary preferred state, and the OR developed from the nucleation stage is maintained at the growth stage. An ideal coherent growth implies coherency in all portions of an interface surrounding the product phase. For the present purpose of studying the OR, we focus on only one interface that contains a fully coincidence-coherent structure. This interface alone is sufficient for determining the OR. An interface containing a fully coincidence-coherent structure must be parallel to rational planes in both lattices. The structures in the two planes must permit the matching vectors be parallel to each other simultaneously. In addition, these parallel vectors must have identical magnitudes. The understanding of this OR is straightforward according to ideal matching between the corresponding vectors. Typical examples of systems containing this type of interface include θ’ precipitates in Al alloys [83], the Laves phase precipitated in Mg alloys [84], and the G phase precipitated from ferrite [85,86]. If the vectors in a matching pair do not have exactly identical magnitudes, the size that the product phase can reach by coherent growth is limited. Semi-coincidence-coherent growth proceeds afterwards.

Frequently, an interface formed by coherent growth is referred to as a coherent interface. The use of the same term for a coherent interface and coincidence-coherent interface does not affect the understanding of the preference of the interfacial structure when the interface is free of dislocations and steps. However, it should be emphasized here that a fully coincidence-coherent structure must remain parallel to the planes of the secondary preferred state, free of steps. One may extend the matching correspondence from 2D to 3D, to calculate the secondary misfit in 3D. Then, it is possible to determine an OR that permits a secondary invariant plane inclined to the planes of the secondary preferred state. In contrast to an irrational coherent interface in the primary preferred state, where the atomic steps are included in the coherent structure of the preferred state, the 2D periodic structure of the secondary preferred state is disrupted by steps connecting different layers of the planes containing the 2D structure of the preferred state. Although there is no calculated secondary misfit in such a secondary invariant plane, the 2D periodic structural units in the secondary preferred state are not preserved along the step riser. The steps are treated as linear defects in a system in a secondary preferred state, and hence, the stepped interfaces are not regarded as fully coincidence-coherent interfaces.

3.2.2. Semi-Coincidence-Coherent Growth

When the secondary misfit is considerable, misfit dislocations will form during the growth of the product phase. The dislocations in a semi-coincidence-coherent interface are usually called secondary dislocations, being distinguished from the dislocations in a semicoherent interface. The Burgers vectors of secondary dislocations must be lattice translation vectors of DSCL [15]. They are usually fractions of lattice vectors of either lattice. The selection of a set of candidates of small DSCL vectors and examination of their availability for secondary dislocations demands a proper construction of a CSL/DSCL model in 3D. The 3D CSL can be extended from the known 2D CSL for the secondary preferred state. Due to the existence of secondary misfit, either lattice needs to be deformed to form an ideal CSL 3D. Then, the Burgers vectors are lattice translation vectors in the constrained DSCL (CDSCL) corresponding to the constrained CSL (CCSL). An example of the construction guided from diffraction patterns can be found in an application to a cementite/austenite system [16].

While little is known about how the dislocations are generated, two simple rules have been found according to the ORs and morphologies of the product phases observed in different materials:

Rule 1: The priority of small Burgers vectors. Dislocations with large Burgers vectors are known to be energetically unfavorable [5]. In a system in the primary preferred state, the Burgers vectors of the dislocations can always be the lattice vectors in the same lattice as the one that represents the preferred state. In contrast, in a system in a secondary preferred state, the preferred state is represented by a CCSL in 2D, but the Burgers vectors are from the CDSCL. The CSL and DSCL are related by a reciprocal theorem [87]. The plane of the CCSL for the secondary preferred state usually contains dense CCSL points, but small CDSCL vectors may not be coplanar with (being parallel is not enough) the above plane. In such a case, small CDSCL vectors in a different plane or another layer tend to serve as the Burgers vectors of the dislocations. The dislocations with a non-coplanar Burgers vector must be associated with steps. A rotation is often needed to make the steps from different sides of the interface meet in an edge-to-edge fashion, as already explained for the stepped interface in the primary preferred state.

Rule 2: Preference for kink-free steps. When steps are preferred, the steps tend to lie along a direction parallel to a pair of good-matching short vectors from different phases, such that the steps are free of kinks in the frame of the CCSL. The step direction is defined by the intersection line where the terrace and step rise meet. For almost all known experimental data (with one known exception), at least one pair of rational (usually low-index) vectors defined by the matching correspondence in the CCSL can actually remain parallel in the observed ORs after the growth stage. The steps, if they exist, are parallel to this rational direction, and the needed rotation around this direction is defined in either phase. This step direction can be parallel either to the normal vectors for the 2D CCSL or to a pair of matching vectors in the planes. Usually, to serve as a step vector, the vectors expressed in both phases are normal to rational planes, as the normal vectors, with the same index in direct space. Such a parallelism condition (between the reciprocal vector and direct vector of the same index) is valid only for the same special low-index vectors in a general crystal system. This means that the steps are usually parallel to a pair of low-index vectors and normal to a pair of low-index planes, in different lattices. Therefore, the rotation in the OR can be analyzed by a 2D model in the overlapped planes normal to the steps. The considerations below are concentrated on these majority cases known to the author. This is in contrast to a system in the primary preferred state, in which a rotation around a pair of exactly parallel low-index vectors belongs to special cases.

Whether a representative rational OR can be preserved at the growth stage largely depends on whether small CDSCL vectors for the Burgers vectors are available in the planes of the secondary preferred state and along short CSL vectors in the plane. Thus, the representative rational OR may either remain unchanged, or be changed to become an irrational OR. These two situations will be considered below separately in some detail.

Rational OR

A rational OR usually occurs when the representative OR is fully invariant at the nucleation stage, i.e., when the vectors in each matching pair in the interfaces are parallel to each other. In a more general case starting from a partial invariant OR, the planes of the secondary preferred state can remain parallel when at least two small DSCL vectors are available in these planes to accommodate the secondary misfit in 2D. In addition, at least a pair of parallel vectors along a row of dense CCSL points can remain parallel. This parallel condition can be satisfied if the misfit between these vectors can be accommodated by the dislocations with the Burgers vector parallel to them. With the above conditions, the representative rational OR can be preserved after semi-coincidence-coherent growth. The following are examples that satisfy the above condition. In the expression of the representative ORs, the parallel planes are the planes of the preferred state, the parallel directions are expressed by the available coplanar Burgers vectors defined in different lattices, and multiple factors, such as 2×, indicate the enlargement of the DSCL vectors to become CSL vectors in the same directions: precipitates Mg₂Sn (β)/matrix (α-Mg) in an Mg-Sn alloy with (1 1 0)_β//(0 0 0 1)_α and (2×) [0 0 1]_β/2//[1 1 2 0]_α/3 (OR1 [34]); precipitates Mg₃₂(Al,Zn)₄₉ (τ)/matrix (α-Mg) in an Mg-Zn-Al alloy with (0 1 0)_τ//(0 0 0 1)_α and (18×) [0 0 1]_τ/9//[2 1 1 0]_α/6 in an Mg alloy [88]. The OR between the Mg₅₄Ag₁₇ (ε’) precipitates and Mg matrix in an Mg-Sn-Ag alloy was observed to be the same as that in the τ/α system [89], indicating the dominant effect of interfacial matching on the OR regardless of a significant difference in precipitate compositions. Usually, the Burgers vector tends to be as small as possible, but the CSL vectors in the same directions as the DSCL vectors for the Burgers vectors (defined in different lattices) may not define the densest CCSL row in the plane. In the above examples, a pair of common symmetry elements in the planes of the secondary preferred state are parallel to each other, resulting in the parallelism of the mirror planes of the two phases. In other cases, rational ORs can be obtained when only a single set of secondary dislocations is needed to accommodate the secondary misfit. The examples include precipitates Al6(Mn,Fe) (p)/matrix (m) in an Al alloy with (001)_p//(3 1 5)_m and (2×) [1 1 0]_p/2//[2 1 1]_m/2 [90], and precipitates TiN/matrix (Ni) in a Ni alloy with (0 1 0)_TiN//(7 1 5)_Ni and (3×) [1 0 1]_TiN/2//[3 1 4]_Ni/6 [33,91]. Because some parallel vectors for defining the rational OR may have high indexes, especially with reference to the matrix, these rational ORs may look irrational. However, they can be treated as rational ORs, since they are small rational vectors of the 2D CCSL for the secondary preferred states, and they are lattice translation vectors of both lattices. It should be noted that the same overlapped planes of preferred state can be obtained with a pair of different ORs, as explained previously [21]. For example, the major interfaces of the Mg₂Sn plates related to the Mg matrix by OR 9 and OR 10 are both parallel to a {0 1 1}_β and a {0 1 1 0}_β, with a <2 1 1 >_β being parallel to a <4 2 2 3 >_β defining an almost perfectly matching direction. However, the orientations of the {0 1 1}_β in the interface plane are twin related in two ORs, as illustrated by Figure 4 in [26]. In the figure, one finds good matching rows along [2 1 1]_β//<4 2 2 3>_β in the major facets with both ORs, but the distributions of the near-matching rows in the two major facets are different. Therefore, the periodic structures of the preferred states in the major facets corresponding to the two ORs are different, though the expressions of the representative rational ORs are similar.

Irrational OR

A reproducible irrational OR occurs when the preferred structure at different layers of terraces is more energetically favorable than that in the same layer, even at the expense of introducing steps. A general reason is that a small CDSCL vector non-coplanar with the planes of the preferred state is selected as the Burgers vector for the interfacial misfit dislocations, as suggested by the rule of the priority of small Burgers vectors. The OR is usually characterized by a small angular difference from the representation rational OR, to enable matching at steps of different heights defined in two phases. According to different types of rotation axes, some details are given below with examples.

• Rotation between the planes of a secondary preferred state

In this type, the rotation axis is along a pair of parallel, short, matching vectors in the planes of the secondary preferred state. A typical example of this type is the habit plane between a cementite (C) plate and austenite (A) matrix related by the Pitsch OR [28], as reported by Howe and Spanos [92]. The representative rational OR can be described by (1 1 3)_A//(1 0 1)_C and 4× [1 1 0]_A/4//[0 1 0]_C/4. To accommodate the misfit in directions other than [1 1 0]_A//[0 1 0]_C, secondary dislocations of [1 1 2]_A/4 or [6 0 2]_C/12 were adopted according to a CCSL/CDSCL model for the Pitsch OR [16]. Similarly, the Burgers vector of the secondary dislocations in the habit plane is [1 1 2]_A/8 or [6 0 2]_C/24 for the T–H OR [29], with the expression of the representative rational OR similar to that for the Pitsch OR (Equation (3)), though the expressions of these ORs in terms of the crystal axes of cementite are significantly different (Equation (2)). The resulting OR can be determined in 2D in the plane normal to the rotation axis. The rotation angles are less than 1° for both the Pitsch OR and the T-H OR, solved under the condition of the existence of a quasi-invariant line [93]. The rotation angle, the orientation of the habit plane containing the quasi-invariant line, the association of the steps with secondary dislocations, and the Burgers vector of the dislocations from the calculations [16,93] are all in strong agreement with the experimental observations [92].

One may also understand the preference of the steps by simply inspecting the stacking of the GMS rows in the plane normal to the rotation axis, similarly to the methods applied in the structural−ledge model [18] and near coincidence site (NCS) model [94] with a rational OR. Namely, steps are preferred when the GMS clusters in different layers are closer than those in the same plane. If only one GMS row in the next plane is close to the origin, the step interface has a unique orientation connecting the nearby GMS rows in different layers, as in the above example. However, if two GMS rows in the adjacent layer(s) are close to the origin with similar distances but at different sides, then there are two choices for the steps to link the GMS rows in different layers. An interesting example of such a case is observed in the habit plane of δ precipitates in a superalloy [94,95]. The representative rational OR can be described by (1 1 1)_γ//(0 1 0)_δ and 2× [1 1 0]_γ/2//[1 0 0]_δ/2, where the subscript γ stands for the fcc matrix. This habit plane prefers to contain a mixture of irregular up-and-down steps of different heights. The Burgers vectors associated with the different steps are the same: [1 0 0]_δ/2 or [1 1 0]_γ/2 according to the CCSL/CDSCL model [95]. Though these Burgers vectors are parallel to the terrace plane, the actual displacement vectors, with the correct direction for the misfit compensation, do not lie in the plane containing dense CCSL points. The rational OR is maintained because the step heights in the two phases are almost identical. In addition, the slight torques due to up and down steps are opposite.

It is also possible that the two types of step structure coexist in the same material. This was observed from a system consisting of a Mo₅Si₃ precipitate (P) and MoSi₂ matrix (M), by Xiao et al. [96], using high-resolution TEM. They found interfaces containing either regular up and down steps or single-inclination steps. In this ceramic material, the steps are preferred to avoid the locations of the structure containing high-energy matching pairs. The representative rational OR can be described by (1 1 0)_p//(0 0 1)_m and [1 1 0]_p//[1 1 0]_m. The interface associated with the regular up and down steps is associated with the above rational OR. The OR associated with the single type of steps is defined by a rotation of 1.8° around [1 1 0]_p//[1 1 0]_m. The measured Burgers vector of the dislocation associated with the steps is [0 0 1]_p/2 or [1 1 0]_m/2. Xiao et al. also suspected that the precipitates with different ORs may have the same rational OR “at the earliest stages of the precipitation reaction” [96] and that the difference in the OR occurs after the misfit dislocations associated with the steps form. Coincidently, the present two-stage approach for reproducible ORs in a general system is consistent with their suspicion for this case.

2.

Rotation within the planes of a secondary preferred state

This type of rotation is around the normal vectors of the planes of the secondary preferred state. In this case, the small CDSL vectors are available in the planes of the secondary preferred state. A major facet will be the step-free interface along the planes of the secondary preferred state. The needed rotation can be understood in terms of steps in the side facets, or the edge of the major facet shared by the side facet. In this sense, the adjustment of the OR at the growth stage is mainly due to the development of (a) preferred side facet(s). This is in contrast to systems in the primary preferred state, which are mainly determined by the major interface, i.e., habit plane. The structure resulting from the rotation may also reduce the interfacial energy of the step-free interface, but this needs to be verified by further studies.

The edge where two facets meet tends to lie along a row of dense CCSL points, so that the good-matching row segments is shared by both facets. The directions of a pair of good-matching vectors can remain parallel if the misfit between them can be accommodated by dislocations with the Burgers vector parallel to these vectors. In this condition, rows of GMS align themselves along the same line, and these rows can be shared by both the major facet and a side facet. However, a row of dense CDSCL points may not be in the same line as a row of dense CDSCL points, even though their directions can be parallel to each other. In this case, following the rule of the priority of small Burgers vectors, the misfit between the rows is accommodated by dislocations that link the rows of GMS in different lines. As a result, the edge of the major facet contains a chain of GMS-row segments linked by steps to improve the degree of matching in the edge. Consequently, the side facet will contain the steps. If the spacings of the GMS rows defined in different lattices are identical, then the representative rational OR will remain unchanged by the formation of the stepped side facet. However, this is not a general case. Due to the difference in the row spacing, there will be a small rotation around the step direction, which is normal to the planes of the secondary preferred state.

These types of stepped side facets are quite common in Mg alloys. Various types of side facets have been observed, as given below.

(1)

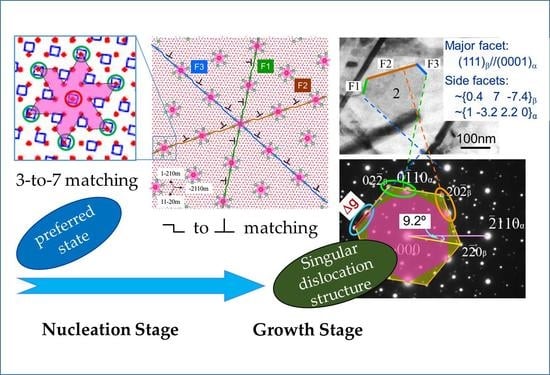
The existence of one major stepped side facet. The OR2 between Mg₂Sn precipitates (β) and a Mg matrix (α) is conventionally expressed by (1 1 0)_β//(0 0 0 1)_α and [1 1 1]_β//[2 1 1 0]_α. Based on the CSL/DSCL model, the representative OR should be expressed as (1 1 0)_β//(0 0 0 1)_α and [1 1 2]_β/2//[5 4 1 0]_α/3. This is because the matching between [1 1 2]_β/2 and [5 4 1 0]_α/3 is much better than the nearly parallel low−index directions of [1 1 1]_β//[2 1 1 0]_α (the direction of the x-axis in Figure 3 in [23]). As seen in Figure 3d, [1 1 2]_β/2 and [4 5 1 0]_α/3 have similar lengths. However, the available CDSCL vector for the Burgers vector-associated steps is [1 1 1]_β/15 or [2 1 1 0]_α/12. This vector is so small that the GMS rows separated by the steps associated with secondary dislocations are virtually continuous [23]. For this system, the rotation within the plane is as small as 0.2°. The resulting quasi-invariant line is in a direction close to [1 1 0 0]_α, whose low-index nature may cause misleading to a result of step-free interface.

(2)

The coexistence of equivalent stepped side facets with different terraces (Figure 3e). In the above example, only one preferred edge between the major facet and the side facet can lie along the good-matching direction of [5 4 1 0]_α/3 and [1 1 2]_β/2. At OR5, approximately expressed as (1 1 1)_β//(0 0 0 1)_α, [1 1 2]_β/2//[4 5 1 0]_α/3 as the representative OR for the CCSL, three pairs of <1 1 2>_β//<4 5 1 0>_α can coexist in the interface (1 1 1)_β//(0 0 0 1)_α [22], as shown in Figure 3d. The smallest CDSCL Burgers vectors for this case are from the family of <1 1 0 0>_α/3. In this case, a rotation to cause one side facet to contain a quasi-invariant line may not be right for other side facets. Then, a small, so-called ternary misfit strain, in the order of 0.1%, is assumed to be accommodated elastically [22]. As a result, three quasi-invariant lines can coexist in different side facets. The final irrational OR, as shown in Figure 3f, can be defined by a rotation angle of ~1.7° between [5 4 1 0]_α/3 and [1 1 2]_β/2.

(3)

The existence of two stepped side facets that share the same preferred terrace plane. The representative OR between Mg₁₇Al₁₂ (β) precipitates and the matrix (α) in a Mg-Al alloy is (0 1 1)_β//(0 0 0 1)_α and [1 1 1]_β/2//[2 1 1 0]_α. In this system, a common shape for the precipitate is a plate, with a habit plane parallel to (0 1 1)_β//(0 0 0 1)_α [97], defined by the planes of the secondary preferred state. The direction of [1 1 1]_β/2//[2 1 1 0]_α defines a pair of good-matching vectors; it is much shorter than the other CCSL vectors in the plane [98]. Naturally, preferred edges of the plate tend to lie along this short CCSL vector. However, the available short DSCL vector ([2 1 1 0]_α/6 or [1 1 1]_β/12) along this direction does not lie in the same row as the dense CCSL. Therefore, the edges prefer to contain GMS-row segments along [2 1 1 0]_α or [1 1 1]_β/2, connected by steps. In this system, the same terrace plane containing [1 1 1]_β/2 and [2 1 1 0]_α is favored by two side facets with steps in different inclinations. However, these two side facets are not crystallographically equivalent. A rotation occurs to favor the edge-to-edge matching of steps in one side facet, with a rotation angle of around 0.5° [97,98]. The minor structural units associated with the steps in this side facet probably have lower energy than that in the other side facet, since this more-favorable side facet usually has a larger area than the other one [99].

3.2.3. Discussion

Interfacial defects play a key role in the development of the OR at the growth stage. Considering the existence of some disagreement in terminology, it is worth clarifying the two major kinds of interfacial defects. In the present consideration, an interfacial dislocation is a defect due to interfacial misfit, i.e., it is a misfit-accommodation dislocation. It is located at the border between adjacent regions containing the preferred state. The low-energy structure of the preferred state, i.e., the state of fit, is the core reference for describing the attribute of the dislocation. The specific matching correspondence in the adjacent regions discontinues at the border by a shift of the Burgers vector of the dislocation. A step is a defect with respect to a flat structure in terraces, and it is located between adjacent terraces. Whether a step can also be treated as a dislocation depends on whether the specific matching correspondence in the preferred state of the interface discontinues at the step.

Following Bollmann [15], two types of preferred states, fully coherent and coincidence coherent, were adopted in the present approach. For a system in the primary preferred state, the use of a unique one-to-one matching correspondence in 3D has garnered a certain degree of consensus for metallic materials, e.g., the Bain correspondence in an fcc/bcc system. With a selected constraint to limit the OR as explained in Section 3.1, the OR, the invariant-line direction, the habit-plane orientation and the interfacial-dislocation structure can all be calculated based on a unique one-to-one matching correspondence. The atomic step structure in an irrational habit plane can be determined by the decomposition of the interface plane into a terrace-ledge-kink structure, but the steps in coherent regions belong to the good-matching area where the preferred state holds. These steps are not considered as misfit-accommodation dislocations. By contrast, the central low-energy structure in an interface in a secondary preferred state is a 2D periodic structure that lies in the terraces. The matching correspondence in the 2D preferred structure is disrupted by the steps. In this sense, the steps should be treated equivalently to misfit dislocations. In some systems involved with ceramic phases, the preferred interface of fit is along a particular pair of planes. Then, the steps may also be treated as misfit dislocations, even though the matching correspondence in the terraces is one to one.

Whether a step can be calculated as a secondary dislocation with a well-defined DSCL vector for the Burgers vector depends on the matching correspondence in 3D for the deformation matrix as an input for the dislocation calculation. If a true invariant line is determined from the selected matching correspondence in 3D, the structure along the invariant line will keep the same matching correspondence for a continuous preferred state in 3D used for the calculation, irrespective of the actual preferred state being primary or secondary. Therefore, no dislocation is calculated to be associated with any steps crossed by this primary or secondary invariant line. For a step to be calculated as a secondary dislocation, the specific matching correspondences in different terraces must be discontinuous. Namely, there is a shift, i.e., the Burgers vector of the dislocation, between the matching correspondences in the structures of the terraces separated by the step. Along a quasi-invariant line, each step is associated with a secondary dislocation, and these dislocations can exactly cancel the misfit in the terrace plane [16,93].

No matter whether secondary dislocations are associated with steps or not, according to a calculation, steps are prominent defects in an interface in a secondary preferred state. To reduce these defects, a stepped interface tends to incline with respect to the terrace plane with an angle as small as possible. This tendency is governed by the minimization of the density of steps rather than that of the calculated dislocations. This explains the preference for a quasi-invariant line over a secondary invariant line, as demonstrated by the habit plane of cementite in an austenite matrix with the Pitsch OR [93]. When the habit plane contains a quasi-invariant line, it is inclined to the terrace plane by ~5°, which is much smaller than ~27°, if the habit plane contains a secondary invariant line. This example clearly explains why a secondary preferred state in 2D is emphasized. Without using a 2D preferred state, a secondary invariant line would be preferred since it passes no dislocation, but a quasi-invariant line passes a set of secondary dislocations associated with the steps.

The coexistence of multiple stepped interfaces with the same terrace and step direction is another feature in a secondary preferred system, distinct from that in the primary preferred state. In a system in the primary preferred state, the direction of the invariant line is fixed in a 2D model, once the rotation axis is given. The corresponding orientation of the habit plane is unique, fully constrained by the direction of an inclined invariant line and the rotation axis [60,70,72,100]. This is because the matching correspondence is unique. In a secondary preferred state, the matching correspondence is unique only in 2D, but not in 3D for calculating of a secondary or a quasi-invariant line. That is why two quasi-invariant lines can form in the habit plane of δ in a superalloy, leading to different inclinations of the step structures [95]. This case is special. Since the step heights in the two phases are almost same, the needed rotations corresponding to the quasi-invariant lines are very small, and hence, the two step structures can coexist in one habit plane with a rational OR. The calculation results provide interpretations consistent with the experimental observations [94].

One may understand the favorable and unfavorable aspects of the steps in terms of structural units in the preferred state. A secondary preferred state could be regarded as a structure consisting of 2D periodic low-energy structural units, relaxed from the atoms near the contacted planes of the secondary preferred state. These will be called major units. By contrast, the steps and dislocations are defects, associated with minor structural units, which are expected to be energetically unfavorable. When misfit exists, a step-free interface along the planes of the secondary preferred state will contain regions of major units with a certain degree of distortion, plus the minor structural units at the cores of the secondary dislocations. If the Burgers vector of the dislocation is large, there will be a relatively large ratio of highly distorted major units, possibly carrying large energy. A preferred structure tends to maximize the less-distorted major units and minimize the minor units. As a result of compromise, an interface containing steps associated with either no dislocation or a secondary dislocation of a smaller Burgers vector forms so that the highly distorted major units in terrace can be replaced by less-distorted major units in different layers of terraces, in addition to dense minor units along the steps. Along this line of thought, one may consider that the kinks can be introduced to replace highly distorted minor units along the step. The kinks can also be described by the other type of minor structural unit. However, the frequent observation of the steps lying along a rational direction indicates a great tendency for eliminating the minor structural units associated with kinks. Therefore, the steps are almost always free of kinks in a system of a secondary preferred state.

The description of the secondary dislocations in the framework of a CSL/DSCL/O-lattice is based on the self-consistent theory proposed by Bollmann [15]. Secondary dislocations in heterophase interfaces have been verified by observing their strain contrast or associated lattice discontinuity. The diffraction contrast of secondary dislocations has been reported for these dislocations, which are either associated with the steps [27,94,101] or not [33]. A CSL/DSCL model needs to be built to provide proper candidates for the Burgers vector (b) for the g⋅b analysis to determine b or verify it. Otherwise, the selection of b from conventional lattice vectors for such a g⋅b analysis may fail to yield a correct result. However, not all secondary dislocations have sufficient diffraction contrast for them to be visible. The Burgers vector can also be identified by applying a Burgers circuit. This again requires the circuit to be built based on the proper DSCL. Different Burgers vectors will be identified if different matching correspondences are selected [102]. While ambiguity in drawing the Burgers circuit does not usually occur for the misfit dislocations in an interface in the primary preferred state, since the one-to-one matching correspondence is often unique and can often be found by intuition, special caution must be exercised when the given system is in a secondary preferred state.

While the present approach only applies the CSL/DSCL model to the systems in the secondary preferred state, this model has also been applied in a similar way to investigate the dislocation characteristics (effective Burgers vector, i.e., a displacement vector) associated with steps (called disconnections [103]) in a habit plane in the primary preferred state. For a step to be calculated as a secondary dislocation in such a system, the matching correspondences must disagree with the one-to-one matching correspondence, as demonstrated by Qiu [77].

It is worth comparing the displacement vector(s) associated with a step in general with a DSCL vector. In any interface that is inclined to a plane that can serve as the terrace plane, e.g., a densely packed plane in either crystal or in the CSL, there will be steps in the interface. Usually, there is always a displacement associated with a pair of vectors on a step riser in different lattices that connects adjacent terraces. Only in a 2D model in the plane normal to the step direction, the step riser vectors are unique and so is the displacement between them. This unique displacement can specify an effective Burgers vector of the step. Consider a special case in which an invariant line lies in this plane of the 2D model, and its direction is inclined with respect to a nearby terrace so that the interface containing the invariant line must contain steps. Whether the invariant line is primary, secondary or quasi, the displacement vector associated with a step must cancel the misfit displacement accumulated in the terrace plane. As a result, the step can play a role in accommodating the misfit in the terrace plane, similarly to a misfit dislocation. While the secondary invariant line or quasi-invariant line (together with the Burgers vector) often lies in the plane of the 2D model, the primary invariant line in a system in the primary system may not be so. However, one can always decompose the vector of the primary invariant line with the components in the terrace plane and riser plane. The misfit displacements associated with the two component vectors must cancel each other, since there can be no net misfit along the invariant line. Therefore, the step can always play a role in cancelling the misfit long the invariant line. However, because the decomposition of the invariant line in a 3D model is variable, the misfit displacement associated with the step-riser vector is not unique, nor is the effective Burgers vector unique.

The effective Burgers vector associated with a step is not usually a rational fraction of a lattice vector, as a characteristic of a DSCL vector, and it is variable with the OR since there is usually an angle between terrace planes defined in two lattices. In a 2D model, however, the proper DSCL vector for the secondary dislocation associated with a step must be very close to the displacement between the riser vectors. This is because the quasi-invariant line passing the steps must thread the O-lattice elements in different terraces. Based on the O-lattice theory [17], the Burgers vector is equal to the secondary misfit displacement of the principal O-lattice vector connecting secondary O-lattice elements at different terraces separated by the dislocation. Therefore, the major part of this DSCL vector is the secondary misfit displacement in the terrace plane, which should be cancelled by the effective Burgers vector. This means that the difference between the DSCL vector and effective Burgers vector is the small misfit displacement associated with the step-riser vector. One may use this relationship to check if the CCSL/CDSCL model is correctly constructed. Only in a special case, when there is no secondary misfit associated with the step-riser vector, the effective Burgers vector associated with a step becomes equal to the DSCL vector for the Burgers vector of the secondary misfit dislocation associated with the step. That is why an effective Burgers vector associated with a step must equal the DSCL vector for the Burgers vector of the secondary dislocation (not a misfit-accommodation dislocation) associated with the step in a CSL grain boundary [1,2], when there is no secondary misfit between the grains. However, an extension from this special case to a heterophase system needs to be approached with caution; the above special case seldom occurs for a heterophase system. A description of the effective Burgers vector in terms of a DSCL vector for such a system is also unnecessary. In addition, while a 2D model is straightforward for demonstrating the difference between a DSCL vector and an effective Burgers vector, the step-riser vectors in a 2D model may not be lattice vectors in the contacted phases in 3D. Thus, the effective Burgers vector determined in 2D may not be a displacement between two small lattice vectors in the riser planes.

While reproducible rational or irrational OR in systems in secondary preferred states can be understood based on their development at the nucleation and growth stages, many details remain unclear. There are multiple selections of secondary preferred states for a given system. What is observed is not really predicable unless the preferred interface contains a dense 2D CCSL without misfit. In general, the densest 2D CCSL and the least secondary misfit do not always occur for one interface simultaneously. The possible compromise and effect of composition and temperature on the interfacial energy associated with different preferred states needs further investigation. Little is known about the misfit-strain energy and effect of its relaxation on the development of the OR. The role of the transformation temperature in this process is expected to be similar to that for the systems in the primary preferred state, i.e., by affecting the driving force to overcome the strain energy and interface energy barrier, and by providing the activation energy for the generation of misfit dislocations. The generation of secondary dislocations, with small Burgers vectors, is likely to be easier than that in a semicoherent interface. However, few experimental results for this process have been reported in the literature. The conservation of substitutional atoms in systems in the secondary preferred state is worth further investigation, since one-to-one atomic correspondence may not be kept.

4. Integrated Approach and Analysis with Δgs

In the present two-stage approach, the reproducible ORs have been rationalized by a natural tendency to form a preferred state at the nucleation stage and to form an optimum dislocation structure at the growth stage. Both are somehow driven by the minimization of the interfacial energy, with and without dislocations. The observed reproducible ORs are usually developed after growth, so their formation is due to the combined effects of nucleation and growth. The resulting reproducible ORs were found to follow some common principles or rules related to the defect structures developed at the growth stage, as summarized in previous reviews [3,19]. The major common features and rules are briefly reviewed below, and their links to the present results are then established.

4.1. Approach in Terms of Singularity

For an OR developed from a phase transformation to be reproducible, it must be associated with an interfacial structure that tends to develop and become stable after the phase transformation. A common feature in a stable interfacial structure is singularity. The consideration based on the singularity in interfaces is based on the hypothesis that a faceted interface with a stable orientation and reproducible OR is associated with a local energy minimum [19]. Such an interface is called a singular interface [1]. A reproducible OR is associated with at least one singular interface attained in a phase transformation. A singularity in interfacial energy must be associated with a singularity in interfacial structure. Thus, one may identify candidates for singular interfaces according to the singular interfacial structures. An interfacial structure is singular if additional types of defects (steps or dislocations) must be added upon a change in the geometry of the interface. For example, a step-free interface is singular in terms of the singularity of the step structure. A change in the orientation of the interface will introduce steps in the interface. This singularity feature also partially limits the OR such that two low-index planes from different phases must be parallel to each other, but with a freedom of in-plane rotation.

A necessary condition for a singular dislocation structure is periodicity in the dislocation configuration. An interface containing periodic dislocations is singular when it is parallel to a principal O-lattice plane [65], defined based on an extension of the O-lattice theory [15,17]. A principal O-lattice plane contains either periodic O-elements (O-points or O-lines) to be separated by dislocations, or one O-plane element, to which a dislocation-free interface must be parallel. Therefore, a singular interface will contain zero, one, two or three sets of periodic dislocations when it is parallel to a principal O-lattice plane containing an O-plane, O-lines or O-points. Additional types of dislocations must be added when the orientation of the interface deviates from the principal O-lattice plane. The discrete nature and limited number of the principal O-lattice planes confine the possible orientations of the interfaces that can contain singular dislocation structures for a given OR. An interface is singular with respect to the OR when the singular structure is possible only at (a) particular OR(s). The OR is fixed when the interface is parallel to an O-plane, and it is partially limited when the interface is parallel to a plane containing the O-lines. It is more convenient to specify the geometry of the principal O-lattice planes in reciprocal space. Singular interfaces defined in terms of principal O-lattice planes will be given the next section, together with a set of simple rules for the corresponding ORs.

4.2. Analysis with Δgs

It is most convenient to study phase-transformation crystallography in reciprocal space, since the measured data are usually from diffraction patterns, recorded in reciprocal space. According to an extension from the O-lattice theory [15], each principal O-lattice plane is normal to at least one reciprocal vector, Δg [65]. Here, Δg = g_α – g_β, where g_α and g_β are reciprocal vectors of lattices α and β, and they must be related by the matching correspondence in reciprocal space. More specifically, for the Δg to define a principal O-lattice plane normal, the associated g_α and g_β must define the planes containing the Burgers vectors of the periodic dislocations in the corresponding principal O-lattice plane. The preferred state development at the nucleation stage is an essential input for specifying the matching correspondence, the set of Burgers vector candidates, and the misfit-deformation matrix as input for the O-lattice calculation. For the primary preferred state, the matching correspondence is often obvious. To define a principal O-lattice plane, the related g_α and g_β are low-index vectors with close orientations. For a secondary preferred state, the related g_α and g_β for a principal O-lattice plane depend on the specific model of the CSL/DSCL for the given system. Regardless of the preferred state, a singular interface containing periodic dislocations must be normal to at least one Δg. The readers are referred to previous reviews for more details of the selection and calculation method [3,104].

The plane edge-matching is an important feature of an interface normal to a Δg. Each Δg is normal to a set of Moiré planes. When the related gs are not parallel to each other, the edges of these planes can meet exactly in the interface normal to the Δg. Therefore, in an interface normal to a group of Δgs, many sets of planes can match in an edge-to-edge fashion, including the terrace planes as required by the edge-to-edge model [74]. Provided that g_α and g_β are related by the matching correspondence, the plane edge-matching geometry means that the misfit displacement in the interface must lie in the matching planes. Accordingly, one can deduce or verify the Burgers vector(s) of the dislocations from the g_α and g_β linked by the Δg(s) normal to the interface. For example, an O-line interface must be normal to a group of Δgs, with the related g_α and g_β in the zone axes of the Burgers vectors of the dislocations in the corresponding phases [19,68,105]. If the interface is parallel to an O-plane, it must be normal to all Δgs linking related g_αsσ and g_βs. The corresponding OR is characterized by all Δgs being parallel to each other, the well-known signature in the diffraction pattern from a pair of twin-related grains [106]. When a singular interface contains a quasi-invariant line, it must be also normal to a group of Δgs, but some g_αs and g_βs connected by the parallel Δgs are not related by the matching correspondence. It can be proved based on the parallel Δgs [16] that the secondary misfit in the terrace is accommodated by the secondary dislocations associated with the steps in a one-to-one fashion. Other facets containing two sets of dislocations along the invariant line are often found to be normal to one Δg [107,108]. Usually, this interface is singular with respect to its orientation but not to the OR.

Singularity in terms of interfacial steps can be also easily identified in reciprocal space. If the step-free feature is on one side of the interface, the interface is normal to a low-index g in the phase at this side. If the step-free feature is on both phases separated by the interface, the interface is normal to a low-index g in each phase. Then, this step-free interface is also normal to the Δg connecting the reciprocal points defined by the parallel low-index gs. A step-free interface is often preferred when one phase or both phases are ceramic, as a specific pair of low-index planes in contact is probably preferred by the compositional component of the interfacial energy.

An interface with a singularity feature can be identified by one or more of the Δg parallelism rules described below. Rule I: g//Δg_I or g//Δg_II; Rule II: Δg_I//Δg_I; Rule III: Δg_II//Δg_II or Δg_II//Δg_CSL-r, where the subscripts I and II denote that the Δg meets the condition for defining a principal O-lattice plane in the primary and secondary preferred states, respectively. The subscript CSL-r means that the Δg is recovered (after using real lattice parameters) from a Δg_CCSL that defines the CCSL plane for the planes of the secondary preferred state in a 3D CCSL/CDSCL model. An interface that follows any one of Δg parallelism rules is parallel to a principal O-lattice plane, normal to either Δg_I or Δg_II and another parallel reciprocal vector. Though the orientation of the interface is fixed by following one rule, only two of the three degrees of the freedom in the OR are fixed. It is possible for an interface to follow two or more rules, or different interfaces surrounding one product particle can follow one or more rules. Then, the OR is fixed. Otherwise, one more constraint is needed to limit the OR.

Rule I applies both the primary and secondary preferred states, for a singular interface in a rational orientation with respect to at least one phase. Rule II and Rule III apply to the primary and secondary preferred states, respectively. Because there is a linear relationship between the related gs, there will be a set of many Δgs parallel to each other, when either Rule II or Rule III works. The magnitudes Δg_I and Δg_II are usually small, since the gs related by a matching correspondence must be close to each other. Therefore, the magnitudes of the parallel Δgs are usually small (e.g., ~|g|/10) when Rule II is obeyed. By contrast, when Δg_II//Δg_CSL-r is obeyed, the magnitudes of the parallel Δgs can be quite large. This case corresponds to the existence of a quasi-invariant line, while Δg_I//Δg_I or Δg_II//Δg_II corresponds to the existence of a true invariant line in the misfit-strain field in 3D. The calculation method for ORs satisfying Δg parallelism rules and a long list of examples have been summarized in previous reviews [3]. The correspondence between various singular interfacial structures and the interfaces that obey different combinations of Δg parallelism rules have been shown by plots in previous reviews [3,19]. The connections of Δg parallelism rules with the preferred structures developed at the growth stage considered in Section 3 will be specified in the next section.

4.3. Integrated Considerations

The specific interfacial singularity and Δg parallelism rules can be integrated with the results of the present two-stage approach. As discussed below, Rules I and III are usually constrained based on the considerations of the OR developed from the two stages. An additional constraint is needed only when Rule II is followed.

The singular interfaces in the primary preferred state with rational ORs and irrational ORs in Section 3.1.4. must follow Rules I and II, respectively. Consider first the interfaces associated with rational ORs. The invariant OR developed at the nucleation stage must follow Rule I, because this OR permits low-index plane containing admissible Burgers vectors in one phase to be parallel to their matching counterpart in different phase. This means that the two gs normal to the low-index planes are parallel to each other, and the corresponding Δg must be parallel to the related gs, as required by Rule I. In addition, there is usually more than one singular rational interface that follows Rule I, making the OR fully fixed. This OR remains after growth whether dislocations are to form or not. If the rational OR starts from a variant OR, it is also possible for Rule I to be obeyed by one singular interface free of steps. In general, this singular interface contains two or three sets of dislocations. The OR is often fixed by the parallelism of a pair of good-matching Burgers vectors in the plane inherited from the representative rational OR. Therefore, based on a consideration of the development of the ORs at the nucleation and growth stages, one can see why the OR is usually fixed when the singular interface follows Rule I, with singularity in the structure of both steps and dislocations.

Consider next the interfaces following Rule II. When the development of an invariant line is preferred, the singular interface contains periodic dislocations between the O-lines. In general, this O-line interface only obeys Rule II, leaving one degree of freedom in the OR unconfined. If the related Burgers vectors defined in different phases are parallel, then the OR is fixed. In this case, the parallelism of Δg_Is, the signature of the existence of an O-line interface, can be directly observed in the overlapped diffraction pattern from the zone axes along these parallel Burgers vectors. Because the directions of parallel Δg_Is and the OR for the parallelism are usually irrational, Rule II makes the irrational OR and irrational orientation of the habit plane easy to measure and understand from a single diffraction pattern [19,68,105]. Such an example has also been found for a habit plane of martensite [109]. If the related Burgers vectors defined in different phases are not parallel, it is still convenient to measure and understand the irrational orientation of the habit plane using Δg_Is from different beam directions. Examples can be found in [50,51,79]. As discussed in Section 3.1, there are various possible constraints for fixing the OR, yielding various ORs that can all obey Rule II.

The ORs for systems in secondary preferred states are relatively simple, as they are usually fully fixed. Because the majority of irrational ORs form by rotations around rational directions, parallelism between gs and Δgs can often be seen directly from the overlapped diffraction patterns taken from the zone axes along the rotation directions. The correspondences of the singular interfacial structures with the Δg parallelism rules for three types of ORs considered in Section 3.2.2. are given below:

• Rational OR. Similar to the case of the primary preferred state, the preferred interface likely follows Rule I when the OR initiated from the nucleation stage is an invariant OR. The OR is fixed by the parallel vectors that are related by matching correspondence in the secondary preferred state. If the OR at the growth stage starts from a partial invariant OR, the interface may only follow Rule I. Then, this interface contains two or three sets of secondary dislocations. Usually, the remaining one degree of freedom in the OR is fixed by the parallelism of a pair of good-matching vectors, with a small DSCL vector also being parallel to them. If this interface contains one set of dislocations between secondary O-lines, it also follows Rule III once. In the appropriate zone axis, one finds a row-matching configuration in an overlapped diffraction pattern, where many Δgs are parallel to gs [90].
• Irrational OR with the rotation axis parallel to good-matching vectors. In this case, the major facet has a terrace-step structure, with the terrace along the planes of a secondary preferred state. It contains a singular dislocation structure consisting of one or two sets of periodic dislocations. This major facet follows Rule III. The OR is fixed by this rule together with the parallelism of the good-matching vectors. A typical example is the irrational habit plane of cementite in an austenite matrix [16].
• Irrational OR with the rotation axis normal to the planes of a secondary preferred state. In this case, the major facet is parallel to the plane of the secondary preferred state, it contains periodic dislocations, and it follows Rule I. The rotation causes a stepped side facet to obey Rule III, so that it contains either a secondary invariant line or quasi-invariant line. The OR is fixed by the two rules, I and III, followed by different facets. For example, the major truncated triangular plate in Figure 3f follows Rule I, and the side facets (marked by F1, F2 or F3) approximately follow Rule III. Each side facet is normal to one Δg in Figure 3g, as indicated by a dashed line. With a slight ternary misfit strain in elastic form, each side facet is normal to a group of Δgs, but these Δgs are out of the range of the diffraction pattern [22]. The resolution of the TEM image in Figure 3f is not high enough to show the steps, but the existence of the steps in the side facets can be verified by the full agreement between the irrational orientations of the side facets with the average orientations of the stepped traces in Figure 3e. More examples of the association of faceted interfaces with Δgs can be found for various precipitates in Mg alloys [23,24,98].

Figure 4 provides a schematic diagram showing a summary of the integrated consideration for reproducible ORs at nucleation and growth stages. For the nucleation range, the governing factor is for the nuclei to have as low a nucleation barrier (ΔG*) as possible. Specific ORs initiated at this stage are subject to the detailed conditions of material system and transformation, especially the lattice parameters of two phases. Low-energy interfaces with either the primary preferred state or various secondary preferred states will be generated, accompanied by the nucleation of the product phase. Usually, the initial OR is not fixed by the preferred state(s), unless there is no misfit. At the growth stage, the governing factor for the ORs to become stable and reproducible is the singular dislocation structure developed in at least one interface.

The factors influencing the final results not only depend on the material system but also on the phase-transformation condition, especially the transformation temperature, which affects the driving force and activation energy for the generation and migration of a dislocation. The OR for an interface to contain a singular dislocation structure must obey one or more Δg parallelism rules. While one Δg parallelism rule only limits two of three degrees of freedom of the OR, the matching correspondence in the preferred state and tendency for the vectors in a matching pair to be parallel can limit Rules I and III in 2D, so that the OR can usually be fixed. If the Burgers vectors for the dislocations defined in two phases are parallel, Rule II can also be applied in 2D, and hence, the OR is fixed. The ellipsis dots in Figure 4 are used to indicate additional results, which also implies uncertainty when multiple selections exist. The selection of secondary preferred states is multiple, possibly affected by the material composition, as well as the density of the CSL points in 2D. Corresponding to a particular secondary preferred state, the coexistence of a couple of reproducible ORs is possible. By contrast, corresponding to the primary preferred state, many more reproducible ORs are possible. When Rule II is the only followed rule, the constraints on the OR are various, depending on the specific system and transformation conditions, as indicated in the chart. Why a particular constraint is selected in a given condition needs further investigation.

In practice, the integrated consideration can be applied to interpret the observed reproducible ORs. Because the reproducible OR permits a singular structure to form in a major preferred interface, it is strongly encouraged to obtain experimental data of the morphology, especially the major preferred interface, with correct indexes in both lattices according to the OR. The experimental data on the preferred interface(s) can not only guide the suggestion of the preferred state but also be used to test the calculation results. It is straightforward if the OR belongs to the invariant OR starting from the nucleation stage and can be inherited during growth, because this is a well-defined rational OR. The parallel planes and directions usually exhibit good-matching characteristics. A major difficulty that one may face is when the reproducible ORs are irrational. The examination of parallel Δgs normal to the faceted interface often helps in rationalizing the observed ORs. Simple steps to facilitate the use of the integrated consideration for interpreting measured ORs and preferred interfaces are given below:

Step 1.

Extract the matching correspondence for the measured OR. This can be done by overlapping the two lattices according to the measured OR or a nearby rational OR if the measured one is irrational. One may apply software such as the PTCLab [61] to plot the overlapped pattern for identifying GMS clusters in the overlapped lattices in different orientations. It is convenient to plot overlapped lattices in the parallel planes, including different layers, as done in the structural-ledge model [18]. The matching correspondence is defined by the matching pair relationship in the GMS cluster at the origin.

Results:

• The preferred state and corresponding matching correspondence. If the correspondence is one to one in 3D, the primary preferred state possible occurs in the interface. Otherwise, the preferred interface is possible in a secondary preferred state, for which a matching correspondence and periodicity for a 2D CCSL must be specified.
• The expression of representative rational OR(s). This expression of parallelism directions and planes with physical meaning can be determined according to the matching correspondence, i.e., nearly parallel matching vectors and the nearly parallel planes containing two matching pairs in the measured OR.
• At least one pair of good-matching vectors that are parallel or nearly parallel and lie in the measured preferred interface. In a preferred interface of good matching, such a pair of vectors must exist.

Step 2.

Examine the distribution of gs and Δgs. This can be performed in the zone axes along the pair of good-matching vectors lying in the preferred interface, determined from Step 1 (Result 3). If no measured overlapped diffraction pattern from the zone axes is available, one can plot the pattern according to the measured OR. In the pattern, compare the rows of gs and direction of Δgs with the orientation of the preferred interface. Then, apply a proper rotation in the range of experimental uncertainty for the exact parallelism of the reciprocal vectors, according to Rule II or III if the measured habit plane or major facet has an irrational orientation. Verify the calculation result with the measurement, to see if the preferred interface is normal to the parallel reciprocal vectors. Otherwise, change the selection of Δg for parallelism until the agreement is achieved, which usually applies only to a system in a secondary preferred state, since some selections may not appear reasonable in reciprocal space [24].

Results:

• An exact OR that obeys one or more Δg parallelism rules, verified by the measured OR and the preferred interface orientation.
• A singular interfacial structure according to the correspondence between the Δg parallelism rules and singular interfacial structures.
• Understanding the reproducible OR based on the singularity in the preferred interface.

Step 3.

Calculate the dislocation structure in the preferred interface(s), if one wishes to find out the details of the singular dislocation structure that governs the preferred OR and interface. This requires a calculation based on the O-lattice theory [15,17] and its extension [65,66], and a construction of the CCSL/CDSCL model in 3D if the system is in a secondary preferred state. The matching correspondence and Burgers vectors based on the preferred state obtained in Step 1 are the essential input of the O-lattice calculation. To find a proper constraint for Rule II with the guidance of an experimental result, one may calculate the dislocation structures in different O-line interfaces by slightly altering the OR in the condition of Rule II and comparing the determined ORs restricted by different constraints with the observation. The free software PTClab [61] is a useful tool for this step.

Results:

• A quantitative description of the dislocation structure, including the Burgers vectors and spacing of the dislocations in the preferred interface.
• Rationalizing the OR in terms of the dislocation structure in the preferred interface.

To verify the dislocation structure with a measurement, a carefully characterized dislocation structure is desirable. This is more demanding than the measurement of the OR and interface orientations.

It is believed that to enable a singular (stable) structure to form in a preferred (stable) interface is the root cause of a reproducible (stable) OR. This link between stable features allows one to identify discrete candidates of ORs in regions confined by preferred states, and to interpret observations in different systems. These candidates greatly restrict the potential reproducible ORs in the 3D space for describing the OR for a given system. As demonstrated in Figure 4, however, a major unsolved problem for a system in the primary preferred state is what singular dislocation structure is to be realized in a given system, when many singular dislocation structures are possible for accommodating the misfit fully or partially. A major unsolved problem for a system in a secondary preferred state is what preferred states are to be realized in a given system, when different secondary preferred states are available. To make progress in addressing the unsolved problems, quantitative investigations that can consolidate the thermodynamics, kinetics and crystallography of a phase transformation are needed. It is hoped that the discrete OR candidates summarized in Figure 4 can facilitate further investigations.

5. Brief Comparison with Related Theories or Models

In the present two-stage approach, the reproducible ORs initiated at the nucleation stage and finalized at the growth stage are considered separately. This approach, in principle, agrees with the general theory of precipitate morphology pioneered by Aaronson, as summarized in [7]. According to the theory, a specific OR is required for the formation of the low-energy interface at the nucleation stage, and “some or all of the low energy interfaces present on the critical nucleus will continue to appear during growth” [7]. This low-energy structure present on the critical nucleus is specified as two types of preferred states in the present study, which yield a “specific” representative OR together. In addition, the matching correspondence defined by a preferred state and a valid range of the OR can be quantitatively identified for a given system. Though only the primary preferred state is taken into consideration, the early theory also indicates that ”the fully coherent structure of such interfaces presumed to obtain during nucleation will be replaced by a partial coherent structure during growth” [7]. An extensive list of early experimental data (before 1970) on the ORs between precipitates and their matrixes together with the interfacial dislocations were provided to verify the theory [7]. These ORs are mainly rational, largely belonging to the invariant OR developed at the nucleation stage according to the symmetry expressed in the ORs. Though the possible effect of the dislocation formation was not taken into consideration in the early theory, these invariant ORs are likely maintained at the growth stage irrespective of the generation of the dislocations. The present approach allows the OR in some systems to be variable at the nucleation stage, and the OR can be further adjusted at the growth stage, as illustrated in Figure 4. The adjustment is required for the formation of singular interfacial structures, which can be quantitatively described with Δg parallelism rules. The analysis in this paper is mainly conceptual, since the associated calculation tools are available in the literature, such as methods for searching the initial OR based on near-row matching [20], for calculating the ORs corresponding to the Δg parallelism rules [3] and for determining the interfacial dislocation structures [17,65,66].

A number of methods have been proposed to predict ORs or preferred interfaces according to optimum matching. Though the criteria and methods for differentiating between good and poor matching are different, the common principle of these methods is that a preferred interface tends to contain a structure of good matching and an optimum OR should enable the formation of such a preferred interface. The present approach was also developed according to this common principle. It is believed that predictions from different methods will overlap to a certain extent, but others may be different since the specific conditions are not the same. These previous studies inspired the development of the present two-stage approach. Below, we provide a short review of major related models and make a brief comparison between them and the method used in the present approach, to clarify the difference.

ORs providing good matching can be searched in either reciprocal space or direct space, by a comparison of matching between lattice points. A method for systematically searching potential ORs in reciprocal space was developed by Ikuhara and Pirouz [110]. They identified the optimum ORs according to the common volume between overlapping spheres centered at reciprocal points from different lattices. This method was extended by Gautam and Howe [111], who additionally used the Δg method to predict both optimum ORs and preferred interfaces. Similar to these methods of systematic searching in reciprocal space, the present study suggests using simple steps in the near-row-matching method [20] to search the ORs corresponding to good matching in direct space. A combined search in direct and reciprocal space for planes that meet the near-row-matching condition is also recommended [25]. The range of search with this method is small, since it aims to find geometries that allow the existence of GMS clusters to serve as potential positions for a preferred state, as the core criterion for the OR. Further adjustment of the OR is often needed at the growth stage, so the resulting OR must meet one or more Δg parallelism rules, and at least one preferred interface is normal to one or more Δgs. This two-step procedure is similar to the approach by Gautam and Howe [111] in that one step mainly yields potential ORs according to an assessment of matching and the other step predicts the interface orientation according to Δgs. However, the further adjustment of the OR to follow the Δg parallelism rule(s) was not considered in their application of the Δgs for the preferred interface. In addition, their approach does not relate the OR with the existence of a preferred state, which is essential for the application of the Δg parallelism rule(s).

Kelly and Zhang [74] proposed a systematic method for predicting the ORs and preferred interfaces based on an edge-to-edge matching geometry examined in direct space. This method also mainly comprises two steps. A direction of good matching is searched in the first step. In the second step, the interplanar distances of the planes in the two phases containing these good-matching directions are compared, and those with small difference are selected. With a proper rotation between the selected planes around the good-matching direction, the edges of the planes in different lattices can match in an edge-to-edge fashion along the good-matching direction. Therefore, the resulting ORs and interfaces are usually irrational. The first step in the near-row-matching method [20] applied here is similar to that suggested in the above edge-to-edge matching model, so the preferred interfaces predicted by both methods will contain the good-matching direction. However, the good-matching features yielded by the second step are different. The good-matching feature, in terms of the near-matching rows and possible existence of GMS clusters for a potential preferred state, is within the overlapped rational planes yielded by the near-row-matching method. By contrast, the good-matching feature is the nearly matched plane edges according to the edge-to-edge matching method [74]. If an invariant line is formed by rotation along the good-matching direction, rotation to obey Rule II or III will also yield an edge-to-edge match between the terraces. This is because the edge-to-edge matching feature is the property of the Moiré planes, which are normal to a Δg, if their related gs are not parallel [65]. In this case, the same OR and irrational habit plane may be predicted by both the edge-to-edge matching model and the present two-stage approach. The present approach is more general in that it can yield both a rational OR associated with a step-free preferred interface and irrational OR associated with a preferred interface containing steps, with the step direction being either along a pair of good-matching rational vectors or not.

An approach for rationalizing preferred interfaces by examining interfacial matching was pioneered by Hall et al. [13]. They proposed the well-known structural-ledge model showing that the preferred interface contains the structural ledges, so the regions of good matching in the stepped interface are greatly increased in comparison with those in the flat interface parallel to the terrace planes. This graphic method was extended in the near coincidence site (NCS) model by Liang and Reynolds [94], such that the good-matching regions consisting of dense NCS in 3D can be identified to guide the prediction or understanding of preferred interfaces. The clusters of GMS are similar to the NCS clusters, though the upper good-matching coefficient for the GMS is increased from 15% to 25% [20]. With a given observed OR, usually permitting a preferred state and singular dislocation structure, both approaches may yield the same preferred interface according to the distribution of good-matching patches (NCS or GMS clusters), separated by dislocations. This graphic approach [13,94] provides a straightforward tool for understanding observed stepped interfaces. While the NCS model claims the advantage of the prediction of the preferred interface without a lattice correspondence, the present approach emphasizes the importance of this missing information in the NCS mode. The matching correspondence is established according to the matching pair relationship in the periodic structure within a GMS cluster around the origin. Though the NCS model can be applied to search for the optimum ORs, this implies a heavy calculation using the graphic method, and it had not been applied before. The near-row-matching method adopted here offers an efficient means for excluding the ORs that do not allow for GMS clusters and fast searching for the range of ORs corresponding to the existence of the GMS clusters. Based on the matching correspondence in the cluster and associated preferred state, the misfit-strain field can be specified, the distribution of the centers of the good-match patches can be calculated in terms of O-elements for any OR with the valid range of the preferred state, and the structure of the misfit dislocations can also be determined based on the O-lattice theory [15,17]. The stepped interfaces predicted by the structural-ledge model [13] and NCS model [94] are usually approximate O-line interfaces that contain good-matching bands along a nearly invariant line, because the input rational OR usually does not meet the O-line condition. Using the analytical method, one can fine tune the OR to meet the Δg parallelism rule corresponding to the exact O-line condition, and determine the precise OR and the interface orientation of the O-line interface, with an appropriate additional constraint.

In summary, for the above comparisons, the presented approach applies conditions of good matching similar to those used in many previous models. Further refinements are made here as guided by experiments. A major refinement is requiring the existence of local periodic GMSs, so that a preferred state can form in the GMS regions in at least one interface at the nucleation stage. This requirement confines the ORs to isolated small ranges in the 3D space for describing the ORs. Within a confined range, the singularity in the structures of preferred interfaces stabilized at the growth stage further restricts the ORs to discrete descriptions. Corresponding to a particular singular interfacial structure, a precise expression of the OR and preferred interface can be determined. However, additional constraints are needed for selection from various small ranges corresponding to different preferred states and from a number of discrete lines (2D) or points (1D) corresponding to singular dislocation structures within a selected small range (3D), unless exact matching is possible. This is an inherent limitation of an approach based on the evaluation of geometrical matching.

To improve the prediction power of the model and to gain an in-depth understanding of the observed OR and associated preferred interface(s) in a given system under a specific phase-transformation condition, the factors of the thermodynamics and kinetics of the phase transformation should be included in further models. The present study has taken the effects of thermodynamics and kinetics into consideration in some conceptual analyses or discussions. While it helps to narrow down and rationalize the selections, quantitative analyses that can combine the thermodynamics, kinetics and crystallography of a phase transformation are needed in further investigations. Molecular-dynamics simulation is a valuable tool for quantitatively studying the thermodynamics, kinetics and crystallography of phase transformations, especially with a variation of temperature and external strain [112]. Therefore, it would be desirable to investigate the evolution of the OR during the nucleation and growth of the new phase with this tool. However, the generation of misfit dislocations seems to be a bottleneck in the current application [38,45]. We look forward to further progress in simulation methods for more-realistic simulation results.

6. Conclusions

The development of the ORs was considered at two stages in order to provide physical insights into the development of reproducible ORs. Our approach specifies the ORs initiated at the nucleation stage in a number of small regions, and it further confines the ORs developed at the growth stage to discrete descriptions. While this study mainly concerns two phases related by a phase transformation, the two-stage approach can be applied, in principle, to other cases in which reproducible ORs are observed, including eutectic reactions, eutectoid reactions, surface reactions and the growth of thin films. In general, it helps to elucidate the reproducible ORs and, possibly, to predict and tailor ORs.

At the nucleation stage, the interface between a surviving nucleus and the matrix must have a low energy so that a low nucleation barrier is attainable. This low-energy structure is defined by a preferred state, characterized by a periodic matching structure, with a correspondence of either one-to-one matching in 3D for the primary preferred state or n-to-m matching in 2D for a secondary preferred state. The matching correspondence in a preferred state confines the initial OR to a small range, which can be represented by one or more representative rational ORs. The potential initial ORs in a given system can be searched systematically using the near-row-matching method according to the periodic distribution of GMSs within a cluster around the origin. The primary preferred state will be predominant whenever it is permitted by the lattice parameters, while different secondary preferred states may coexist in a system. The effect of preexisting interfaces on the observed OR depends on the crystals joining at the preexisting interfaces, the interface governing the preferred state, and the available driving force to surpass the misfit-strain energy.

The change from the initial OR at the growth stage is caused by the misfit with respect to the preferred state developed at the nucleation stage. The adjustment of the OR must ensure that the preferred state is sustained locally in the interfaces. In the meantime, the developed OR tends to provide the geometry that permits a singular interfacial structure to form in at least one interface, usually in the habit plane. In a singular structure, the dislocations must be periodic and form in as few types as possible. The ORs associated with the singular interfaces can be specified by following at least one of three Δg parallelism rules. When the OR initiated at the nucleation stage is invariant, it permits singular interface(s) to form, so the representative rational OR can be maintained at the growth stage. The corresponding reproducible OR is associated with (a) step-free preferred interface(s) following Rule I. A singular dislocation structure may develop at the expense of adding interfacial steps. The existence of interfacial steps in preferred interfaces is a major cause of reproducible irrational ORs, because the step heights in the two phases are usually different, and hence, a small rotation is needed for the steps in the different phases to match each other. The rotation must obey Δg parallelism Rule II or III.

In a system in the primary preferred state, the reproducible irrational ORs usually obey Δg parallelism Rule II, with the parallel Δgs normal to the habit plane containing a single set of dislocations. The overall misfit strain could be either fully relaxed by multiple sets of interfacial dislocations or partially relaxed by only one set of dislocation loops. Different factors for fixing the remaining one degree of freedom in the OR after applying Rule II have been discussed, but fully understanding the influencing factors in different phase-transformation conditions remains a challenging task for future studies.

In a system in a secondary preferred state, steps are needed when small CDSCL vectors are not available to serve as the Burgers vectors of the optimum secondary dislocations on the plane of the secondary preferred state or on the terrace planes of side facets. The resulting irrational ORs usually obey Δg parallelism Rule III, so the secondary misfit in the terrace plane can be cancelled by the displacement associated with the steps. The step direction is usually along a pair of the parallel low-index vectors, either normal to or lying on the planes of the secondary preferred state. With this condition and Rule III, the OR is fully fixed.

While the present approach provides a general tool for rationalizing observations of reproducible ORs and predicting potential ORs, it cannot provide a unique prediction unless the system is free of misfit. The selection of the preferred state in a secondary preferred state is likely to be affected by the composition of the given alloy and interaction of the misfit strain with the environment. The misfit-accommodation process is closely related to the specific condition of the phase transformation, especially the transformation temperature. An improved model is required to take the alloy composition and phase-transformation condition into consideration. This requirement calls for a consolidation of the thermodynamics, kinetics and crystallography of phase transformations.