1. Introduction
The study of the phase diagrams involving copper oxide CuO and alkaline or alkaline earth oxides demonstrated the occurrence of phases characterized by common structural features with general formula A
xCuO
2, where typically x = 1 for A = Na, K and 0.67 < x < 0.90 for A = Ca, Sr, Ba. Alkaline-based cuprates, like NaCuO
2 and KCuO
2, consist of alkaline layers [
1,
2,
3,
4] interpenetrated by edge-sharing CuO
2 ladders. The different size of Na and K cations, rules the periodic arrangement CuO
2 stripes and cations. Octahedral sites, formed by oxygen atoms of adjacent CuO
2 chains, are occupied by the alkaline cations in a 1:1 ratio with the CuO
2 units. For A = Ca
2+, Sr
2+ or Ba
2+, the structure remains strictly related to that of the corresponding alkaline-based compounds but, as a result of the increased atomic size, only a fraction of the octahedral sites is occupied and the compound results to be non-stoichiometric. Indeed, as the ionic radii of the alkaline-earth increases, A
2+/Cu decreases progressively as evidenced by the compositions reported in literature [
5,
6,
7,
8] and summarized in
Table 1. The remarkable compositional flexibility is demonstrated by the occurrence of Na-based compounds with chemical composition Na
1.66CuO
2 showing a stable excess of Na
+ ions [
9]. So far, K-based off-stoichiometric K
1.5CuO
2 can be efficiently fabricated [
10], being the inferior content of K likely ascribable to the similar correlation between ionic radii and chemical composition observed for the alkaline-earth group of cuprates. Nevertheless, several structural studies accounted that this family of cuprates represent a prototypical example of composite crystal [
11,
12,
13]. Indeed, the crystalline phase is composed of two distinct sub-structures associated to the A cations and CuO
2 symmetries, respectively. The different symmetry and periodicity of the two sub-systems give rise to incommensurate displacive modulation observed in all the off-stoichiometric compounds [
9,
10,
14,
15,
16,
17,
18]. The mismatch of the two sub-units, ruling the A/Cu balance, is generally confined to a single fundamental periodicity giving rise to a mono-dimensional incommensurate modulation.
It is worth to recall that, similarly to the Cu-based family, a series of 1D layered compounds showing similar incommensurate modulated structure was discovered for alkaline and alkaline-earth cobalt oxides [
19,
20]. The layered Na
0.83CoO
2 composite crystal crystalizes in a triclinic symmetry and possess interesting thermoelectric properties [
20].
The occurrence of infinite edge-sharing CuO
2 chains is a structural character of few materials and a series of unusual physical and chemical properties are featuring this family of compounds. Ordered mono-dimensional 1D spin arrangement was found in the SrCu
2O
3 and Sr
14Cu
24O
41 compounds [
21,
22,
23]. The antiferromagnetic (AFM) ordering observed in Sr
14Cu
24O
41 below 60 K has been related to the spin orientation predominantly perpendicular to the 1D CuO
2 chains [
22]. This is confirmed by the observation of similar antiferromagnetic coupling in Sr
0.73CuO
2 [
5,
24], below 10 K. Analogously, incommensurately modulated calcium cuprates are characterized at low temperature by AFM coupling [
17]. The magnetic properties of such cuprates show a complex behavior associated to the interplay of different 1D spin configurations (spin dimers, alternating Heisemberg chains, etc.). The off-stoichiometry is compensated by hole-doping of the cuprate ribbons with the proper balance of Cu
2+/Cu
3+ ratio. Interestingly, the Cu valence is not randomly distributed, but it is observed charge ordering giving rise to periodic magnetic correlations [
25]. Recent inelastic neutron scattering studies on (Ca,Y)
0.82CuO
2 disclosed complex ferromagnetic frustrated interactions involving adjacent CuO
2 chains having a mono-dimensional (1D) AFM ordering [
26].
Nevertheless, the Ca
0.83CuO
2 system exhibits a remarkable activity in the catalytic oxidation of volatile organic compounds, as well as the unusual ability to adsorb gases such as NOx, CO, CO
2, with strong selectivity toward NO
x [
27]. The reversibility of the sorption process, induced by thermal treatments, could make Ca
xCuO
2 with 0.824< x <0.84 a suitable material for de-NOx applications [
27,
28]. Furthermore, Ca-based cuprates gathered increasing attention in the field of nanocatalysis for the synthesis of different aromatic aldehydes, in solvent-free modes [
29]. These novel applications demand the knowledge of the structural properties at the high-temperature regime suitable for catalytic and gas up-taking applications. Up to now, the structural studies of the off-stoichiometric cuprates was dedicated to the low temperature properties. In this work we present valuable insights obtained by the structural analysis of the Ca
0.83CuO
2 compound carried out by increasing the temperature up to 1073 K. The detailed structure determination of such complex incommensurate composite crystal was successfully achieved by introducing the superspace approach [
13]. The experiments were performed adopting a time-resolved mode with a Debye–Scherrer diffractometer implemented in the BM08 beamline of ESRF large facility. The Rietveld refinements performed on the powder diffraction data unveil the complex evolution of the Ca
0.83CuO
2 composite crystal at high-temperature conditions.
3. Results and Discussion
In earlier works, ED and HREM investigations [
14,
15] addressed the structural study of Ca and Ba based cuprates. ED patterns manifest the typical features of composite crystals showing diffraction spots associated to two independent lattices. The indexing of the separated groups of the main reflections provided the following cell constants [
15]:
- (1)
a = 2.80 Å, b = 6.32 Å, c = 10.57 Å (Orthorhombic Fmmm symmetry)
- (2)
a = 3.36 Å, b = 6.32 Å, c = 5.47 Å, β = 104.9° (Monoclinic C2/m symmetry)
The former is consistent with the typical arrangement of copper-oxygen chains in A
xCuO
2 compounds [
14,
15,
16] and it is readily assigned to CuO
2 sublattice, the latter being clearly related to Ca sub-lattice periodicity. This interpretation agrees with the ED study that we performed on the samples fabricated and used for the high-temperature diffraction experiments. The indexing of spots observed in ED data by using Ca and CuO
2 reciprocal lattices is presented in the
Supplementary Material Figure S1. As it is illustrated in the
Figure 1, the composite crystal Ca
0.83CuO
2 is formed by the interpenetrating of the distinct lattices with their own translational symmetry. When the ratio of the unit cell volumes of the two sublattices is irrational, the two sub-structures coexist with off-stoichiometric compositions. The mutual interaction of Ca layers and CuO
2 ribbons is accompanied by structural modulation. As a result, the diffraction pattern of a composite crystal is the superimposition of the diffraction patterns of the two sublattices and satellite reflections. In the frame of the superspace approach the (3D + 1)-dimensional structure of a composite crystal, the first sub-unit is associated to the
hkl0 indices, while the indices of the second one are given by
0klm with a shared reciprocal plane with indices
0kl0. Reflections
hklm are the result of the mutual interaction of the two subsystems. The whole ED pattern is indexed by adopting the diffraction vector:
where
a*,
b* and
c* are related to one sub-lattice, whereas the modulation vector
q = α
a* + β
b* + γ
c* represents the incommensurate periodicity of the second sub-lattice. The incommensurate crystal structure of Ca
0.83CuO
2 was solved by Miyazaki et al. [
17] on the basis of both x-ray and neutron powder diffraction data. The composite crystal was represented by assigning the non-conventional space group F2/m(1 + α 0 γ)0s with a modulation vector assuming the form
q = x
a*CuO2 + (1 − x)
c*CuO2. Indeed, the authors converted the monoclinic Ca sub-lattice by adapting a F centered cell with the following constants: a = 3.36 Å, b = 6.32 Å, c = 10.59 Å, β = 92.99°. This model represents the first application of the superspace formalism to the structure description of the Ca
0.83CuO
2 incommensurate composite crystal at room temperature [
17]. In the actual work, we define the composite crystal with a different approach based on the monoclinic lattice associated to the Ca lattice. This new setting is illustrated in
Figure 1 wherein both CuO
2 and Ca sub-units are referred to a monoclinic symmetry having the
c constant coinciding with 5.47 Å, but with different monoclinic angle.
The base reciprocal vectors for the composite structure are correlated by the (3 + 1)-dimensional matrix:
In this frame, the superspace symmetry for the CuO
2 sub-structure is P2
1/m(α0)0s, characterized by non-primitive translation conforming the m
s mirror. The symmetry rules define the modulation vector as
q= α
a* + γ
c* having α equivalent to both the x compositional parameter Ca
xCuO
2 and the a
CuO2/a
Ca fraction [
14,
15]. The fundamental undistorted structure of CuO
2 is constituted by a special position for Cu and two independent positions for O with coordinates (x, ¼, z). The Ca atom is positioned at the origin of the second basic sub-structure. The modulation of the three atomic species was defined by the Fourier modulation function:
where x
4 represents the four-dimensional variable in the superspace, and the A
i and B
i parameters allowed by the symmetry are refined to determine the displacive modulation for each atomic site. To finely describe the modulation function of the atomic species, we introduced the first and second order of the cosine and sine components of the Fourier series.
The (3D + 1)-dimensional crystal data of the Rietveld refinement obtained from the RT diffraction data are summarized in the
Table 2. The structural refinement achieved the agreement factors R
p = 2.26% R
wp = 3.07% and the Rietveld output plot is depicted in
Supplementary Material Figure S2. The refined modulation vector
q = 0.83057(7)
a* + 0.0032(3)
c* agrees with the nominal chemical composition. The a
CuO2 cell constant can be related to a
Ca with the simple relation 6a
CuO2 = 5a
Ca, from which a
CuO2/a
Ca = 5/6 = 0.833, therefore, the chemical formula could be suitably indicated as Ca
5Cu
6O
12.
Table S1 resumes the refined values of the A
i and B
i amplitudes associated to the fractional basic coordinates. Concerning the Cu-O interactions, the four-fold coordination is far from the ideal planar configuration being perturbed by the propagation of a tilted wave along the ribbons. The Cu-O distances are characterized by an oscillating mean bond length ranging from 2.05 to 1.85 Å with a global average of 1.93 Å. The distortion of the CuO
2 chains is related to the periodic charge ordering well described by plotting the modulated Cu-O lengths calculated from the (3D + 1)-dimensional model. The sequence of the in-phase shrinkages and expansions of the square coordination can be correlated with the mixed valence Cu
2+/Cu
3+. The bond valence (BV) plot of
Figure 2c demonstrates that the Cu oxidation alternates between 2+ and 3+ limits, with the same period of Cu-O modulated interactions. The assigned valence must be interpreted bearing in mind that, for such a complex structure, the bond valence evaluation is not straightforward. Therefore, the upper region of the curve approaching 2.9 value was attributed to 3+ valence, whereas the region of the curve ranging from 1.8 to 2.2 likely corresponds to Cu
2+.
As a result, considering a commensurate six-fold periodicity, the CuO
2 chains are constituted by the sequence Cu
2+-Cu
2+-Cu
3+-Cu
2+-Cu
2+-Cu
3+. This charge ordering topology is in agreement with the spin hole arrangement formulated by M. Isobe at al. [
18] for the Ca
0.824CuO
2 composition and with former studies treating the Ca
0.83CuO
2 magnetic properties [
14,
15,
16].
Nevertheless, the wave-like modulation of oxygen sites determines the major distortions of the environment of Ca atoms with the occurrence of remarkably distorted octahedral sites (see
Figure 3). In this sense, the mutual interplay of the two sub-units is essentially ruled by the displacive modulation of the oxygen sites.
The hypersection of the (3D + 1)-dimensional composite crystal [
11] corresponding to
q = 5/6
a* (the γ is approximated to 0 value) provides a commensurate superstructure having unit cell constants a = 6a
CuO2 = 5a
Ca, b = b
Ca, c= c
Ca and β = 104.9° with P2
1/a symmetry (the crystal data are reported in the
Table S2). The structure model consists of three independent positions for Cu and Ca atoms, having general coordinates (x,¼,½) and (x,0,0), respectively, and 6 sites for the oxygen atoms. The
Figure 3 represents the commensurate five-fold superstructure where the Ca octahedral coordination and structural modulation of CuO
2 stripes are emphasized.
The sequence of edge-shared octahedra occupied by Ca
2+ is discontinuous and after the third occupied site, the successive ideal Ca site is vacant. This cluster is represented in the
Figure 3 by the Ca2-Ca1-Ca2 labelling being the Ca2 site markedly distorted. The next two octahedral sites indicated as Ca3 are rotated of about 90° with respect the previous orientation. The Ca2 coordination is affected by a strong deviation from the regular octahedral condition with at least 7 Ca-O short interactions ranging around 2.08 Å.
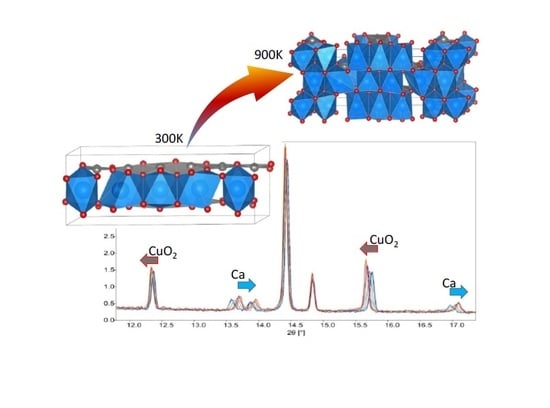
The high-temperature trend recorded in synchrotron diffraction experiments highlights the almost independent thermal expansion of the two sub-structures constituting the composite crystal.
In the
Supplementary Material Figure S3, the overlay of the diffraction patterns collected in the temperature range 320–950 K is shown. Interestingly, the reflections associated to Ca sub-lattice are progressively shifted towards high 2θ region as the temperature increases. For each temperature step, Rietveld refinements was undertaken. The monoclinic model with P2
1/m(α0γ)0s is adopted for the overall temperature range and no change of symmetry of the (3D + 1)-structure was observed as it is indicated by the good agreement factors achieved for Rietveld refinements carried out for the high-temperature diffraction patterns (as an example see
Supplementary Material Figure S4). The
Figure 4 illustrates the evolution of the unit cell constants for both sub-lattices and corresponding change of the
q vector against temperature. Upon heating, the composite crystal undergoes an adaptive structural change featured by the shrinking of Ca sub-structure. The onset of this structural transition corresponds approximately to 540 K as it is well drawn by the change of the
q vector periodicity as well as the evolution of the
a lattice parameter for both sub-structures (see
Figure 4 a,b). Conversely, as it is illustrated also by the
Figure 4d, by increasing the temperature, the CuO
2 sub-unit expands as expected. Beyond 500 K, the α parameter of the
q modulation vector exhibits a marked increment moving from 0.830 to 0.851; the γ component abruptly increases and relaxes beyond 700 K. The deviation from a commensurate 5/6 periodicity indicates a recombination of the compositional Ca/Cu ratio mediated by the oxygen modulation. This is particularly evident by plotting the Cu-O lengths calculated for the 890 K structure wherein the structural recombination of the Ca-O interactions impacts on the CuO
2 chains. The
Figure 2b shows that the Cu-O modulated lengths are spanned in a broad range and the Cu environment departs from the periodic alternation of short/long interactions observed in the phase stable at RT. The BV evaluation reported in the
Figure 2d indicates a complex distribution of the mixed valence 2+/3+ for Cu and the calculated curve is actually the convolution of two periodic wave-like periodicities. The additional curve introduced to fit the BV profile shows a maximal value around 2.3 and the convolution of the two calculated Gaussian profiles point out a consistent rising of the Cu
2+ content.
The average valence for Cu, extended throughout the incommensurate composite crystal, is around 2.28 with a slight but not negligible decrement with respect the oxidation state of 2.35 observed at room temperature. The shortening of the Ca-Ca distances rises the positive charge density in Ca
xCuO
2 compound which is, in turn, compensated by a decrease of Cu
3+ occupancy alongside CuO
2 ribbons. The complex curve of the BV summation can be also interpreted by recalling earlier studies related to the synthesis of such compound under unconventional conditions [
31,
32].
In particular, X.M. Qin and co-authors [
32] explored high-temperature and high-pressure conditions to ascertain the stability of the off-stoichiometry Ca
xCuO
2 compounds. They accounted that, by crossing 1028 K, Ca
0.85CuO
2 decomposes into Ca
2CuO
3 + CaO at ambient pressure. Indeed, the additional curve convoluted in the BV periodicity could be related to the compositional instability, indicating an incipient phase separation of CaO and consequent formation of Ca
2CuO
3. Nevertheless, we did not notice the occurrence of CaO phase in the synchrotron diffraction pattern collected at high-temperature limit. Considering the crystal structure at 890 K, it is possible to define a new commensurate superstructure based on the broad assumption that for
q = 0.851
a* + 0
c* ≈ 6/7a* so as 6a
Ca ≈ 7a
CuO2. The six-fold superstructure corresponding to the ideal Ca
6Cu
7O
14 composition has a triclinic P-1 symmetry with seven independent sites for Cu and Ca, respectively (see
Table S3). Two symmetrically special sites of Ca atoms are occupied only by half in order to preserve compositional requirements. It is worth to stress that the new chemical formula is consistent to the redistribution of Ca and Cu cations across the average composite matrix and cannot be intended as a substantial increment of Cu amount. Hence, the chemical content remains constant but with a different spatial distribution over the average unitary crystal volume. In the six-fold supercell, depicted in
Figure 5, the main difference with respect the RT structure relies on the more regular octahedral environments hosting Ca
2+ ions. Among the seven sites for Ca, only Ca6 is affected by a strong distortion of the oxygen coordination with the occurrence of 7 Ca-O short interactions. The Ca6 site can be thus associated to the Ca2 of the Ca
5Cu
6O
12 RT phase, but in the actual structure this complex environment involves only 1/7, rather than 1/3, of the occupied interstices. The CuO
2 ribbons show the wave-like distortion already observed at low temperature.