Next Article in Journal
Broadband Asymmetric Propagation in Pillared Meta-Plates
Next Article in Special Issue
New Rod-Like H-Bonded Assembly Systems: Mesomorphic and Geometrical Aspects
Previous Article in Journal
Quantitative Structure–Property Relationships from Experiments for CH4 Storage and Delivery by Metal–Organic Frameworks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 10
Issue 8
10.3390/cryst10080701
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Optical and Geometrical Characterizations of Non-Linear Supramolecular Liquid Crystal Complexes

by
Hoda A. Ahmed
1,2,
Mohamed Hagar
2,3,*,
Omaima A. Alhaddad
4 and
Ayman A. Zaki
5,6,*
1
Faculty of Science, Department of Chemistry, Cairo University, Cairo 12613, Egypt
2
College of Sciences, Chemistry Department, Taibah University, Yanbu 30799, Saudi Arabia
3
Faculty of Science, Chemistry Department, Alexandria University, Alexandria 21321, Egypt
4
College of Sciences, Chemistry Department, Madina Monawara, Taibah University, Al-Madina 30002, Saudi Arabia
5
College of Sciences, Physics Department, Taibah University, Yanbu 30799, Saudi Arabia
6
Faculty of Sciences, Physics Department, Banha University, Banha 13518, Egypt
*
Authors to whom correspondence should be addressed.
Crystals 2020, 10(8), 701; https://doi.org/10.3390/cryst10080701
Submission received: 18 July 2020 / Revised: 3 August 2020 / Accepted: 5 August 2020 / Published: 14 August 2020
(This article belongs to the Special Issue Optical and Molecular Aspects of Liquid Crystals)
Browse Figures
Versions Notes

Abstract

:
Nonlinear architecture liquid crystalline materials of supramolecular 1:1 H-bonded complexes (I/II and I/III) were prepared through a self-assembly intermolecular interaction between azopyridine (I) and 4-n-alkoxybenzoic acid (II) as well as 4-n-alkoxyphenylazo benzoic acid (III). The H-bond formation of the prepared supramolecular hydrogen bonded (SMHB) complexes was confirmed by Fourier-transform infrared spectroscopy (FT-IR) and differential scanning calorimetry (DSC). Optical and mesomorphic behaviors of the prepared complexes were studied by polarized optical microscopy (POM) as well as DSC. Theoretical calculations were performed by the density functional theory (DFT) and used to predict the molecular geometries of the synthesized complexes, and the results were used to explain the experimental mesomorphic and optical properties in terms of their estimated thermal parameters. Ordinary and extraordinary refractive indices as well as birefringence at different temperatures were investigated for each sample using an Abbe refractometer and modified spectrophotometer techniques. Microscopic and macroscopic order parameters were calculated for individual compounds and their supramolecular complexes.

Graphical Abstract

1. Introduction

Many liquid crystalline compounds display one or more distinct mesophases depending on the basis of the molecular arrangement such as nematic (N) and smectic phases [1,2,3]. Optical properties, such as absorbance, transmittance, refractive index and birefringence are very important for liquid crystal (LC) applications. Transmission with a long temperature range was measured for nematic LC [4]. Additionally, the index of refraction and birefringence were determined by wedge and Newton’s rings techniques for LC in the N-Sm phase [5,6,7,8]. Yildiz et al. used Abbe refractometer and rotating-analyzer techniques for measuring ordinary (no) and extraordinary (ne) refractive indices and birefringence (Δn) [5,9]. In addition, the dependence of birefringence on temperature was studied for LCs [10,11,12,13,14,15,16,17,18]. The factors of the birefringence, of thermal stability and order parameter were also reported [19,20]. Recently, supramolecular liquid crystals (SMLCs) intensively attracted the attention of many scientific research studies [21,22,23,24,25,26,27,28,29,30,31]. Among the self-assembly method LCs is H-bonding intermolecular interactions with noncovalent bonds [32,33,34,35,36]. Among the H-bond acceptors and donors, pyridine derivatives and carboxylic acids were shown to be the best choice in many studies. Furthermore, the use of multifunctional compounds in the establishment of noncovalent interaction could produce good properties of SMLC network architectures [37,38]. The photoresponsive properties of azopyridines make them a good choice for liquid-crystal materials due to their aptitude for thermal and photo trans-cis-isomerisation [39,40]. Recently, the designing of new structures according to computational prediction attracts the attention of many researchers [39,41,42,43,44,45,46,47,48,49,50]. Studying the optical parameters of the LCs requires some information about the molecular geometries. The DFT method becomes an effective tool for its excellent performance and consistency with the experimental data [27,28,43,48,51,52,53,54,55,56,57,58,59,60,61].
The aim of the present work was to design angular H-bonded supramolecular complexes (Scheme 1) of new conformations and investigate their optical properties using different techniques. In addition, DFT theoretical calculations were carried out to estimate the molecular geometry of the prepared H-bonded complexes as well as to predict their thermal parameters. Ordinary and extraordinary refractive indices, birefringence and order parameters were measured and compared for all supramolecular H-bonded complexes.

2. Experimental

Preparation of 1:1 Supramolecular Complexes

4-n-Octyloxybenzoic acid (II) was purchased from Merck Company (Germany). The transition temperature of the azopyridine-based derivative (I) was checked with the previously reported one [62,63].
Equal molar amounts of the individual components of the target SMHBLCs complex (I/II and I/III) was melted with stirring till an intimate blend then cooled to room temperature (Scheme 2) [64,65].

3. Results and Discussion

3.1. FT-IR Spectroscopic Confirmation of SMHB Complex Formation

The spectral data of the FT-IR were recorded in order to prove the H-bonded supramolecular complex formation. The spectra were measured for individual components as well as their supramolecular complexes I/II and I/III (Figure 1). The C=O stretching vibration is well known to be at 1681 cm−1 [66,67,68]. The formation of the H-bonding between the proton acceptor nitrogen atom and the COOH group of the H-donor of acid exchanged the dimeric H-bonds of carboxylic acid.
The sharing of the hydroxyl group of the COOH in H-bonding decreased its vibrational strength. As shown from Table 1, theoretically, the length of OH-bond increased from 0.97573 Å with H-bonding to 1.032 and 1.038 Å for complexes I/II and I/III, respectively. Moreover, its stretching vibration decreased to 2561.3 cm−1 instead of 3662.6 cm−1 of the free acid for the complex I/II. Experimental FT-IR spectra illustrated that there was no considerable impact of the H-bonding on the C=O strength vibration, where, there was only a 4 cm−1 decrease (ύC=O = 1681.7 cm−1). However, the ester linkage of the azopyridine base C=O group influenced the stretching vibration; the wavenumber of C=O of the complex I/II increased from 1724.4 to 1728.1 cm−1 and 1734.0 cm−1 for the other, I/III. Furthermore, an important provident of the H-bonding in the supramolecular complexes (SMCs) is the existence of three Fermi resonating frequencies of the OH group, A-, B- and C-types [50,69,70,71,72,73,74]. The Fermi band of the A type existed in the range of 2912 to 2835 cm−1 under the C-H stretching vibrations. Furthermore, the important vibrational frequency of the O-H (B-type) at 2352 cm−1 could be assigned to the in-plane bending stretching vibration. However, the Fermi band of the C-type of the interaction of the stretching vibration of the OH and the overtone of the torsional effect was in the range of 1901.3 and 1902.8 cm−1.

3.2. Mesomorphic Properties

Differential scanning calorimetry (DSC) measurements were recorded to study the mesomorphic transition behavior of 1:1 SMHB complexes I/II and I/III, and the type of mesophases was proved by measuring the polarized optical microscopy (POM). Thermal analyses of these complexes were recorded from the second heating scan and the DSC profiles upon heating/cooling cycles for I/II and I/III SMHB complexes (Figure S1, Supplementary Materials). Illustrative textures of the investigated mesophases from the POM are shown in Figure 2. The 1:1 molar supramolecular complex formation can also be confirmed from the crystallization peak symmetry (Figure S1).
The azopyridine (I) mesophase behavior was observed to have a smectic A (SmA) phase with a stability of 121.5 °C [65,75], while the 4-octyloxybenzoic acid (II) was dimorphic, exhibiting smectic C (SmC) and nematic (N) phases with a mesomorphic stability of 147 °C [62,63], and 4-octyloxy phenylazobenzoic acid (III) exhibited a SmC phase with a wide range of stability and an N phase with a very small stability range [75]. Therefore, the investigation of the mesophase behavior of the supramolecular complexes resulted from mixing the compounds with different mesogenic lengths (I/II and I/III) is an interesting study. Transition temperatures and associated enthalpies of transitions for the individual base and acids moiety as well as their corresponding 1:1 molar supramolecular complexes (I/II and I/III) are listed in Table 2. As can be seen from Table 2, upon heating, the complex I/II indicated an endothermic peak with 27.4 kJ/mol followed by a small endothermic smectogenic peak with 1.5 kJ/mol. The complex I/III illustrated a strong endothermic peak with 46.0 kJ/mol ascribed to the melting process, and an endothermic peak with 7.2 kJ/mol was assigned to the SmA-N transition followed by a small peak of nematic transition with 3.5 kJ/mol. Thus, the variation of peak enthalpy changed between the individual compounds and their SMHB complexes, which may be attributed to the different molecular geometries of each component. Data in Table 2 show that the I/II complex exhibited a monomorphic smectic A phase (SmA) with a thermal stability of 104.6 °C, while the second complex I/III possessed a dimorphic phase of enantiotropic SmC and N meophases with a higher thermal stability (198.7 °C). It can be concluded that the incorporation of azophenyl moiety in the acid component III leads to an enhancement of the thermal stability (i.e., the mesogenic core length is influenced by the mesophase stability) of their supramolecular complex I/III rather than I/II.

3.3. DFT Calculations

The DFT calculations were performed on a B3LYP 6-31G (d,p) basis set in the gas phase set out by Gaussian 09 software; see supplementary data. Due to the presence of many conformers of the base (I), the thermal parameters of two conformers (Ia and Ib) of less sterically hindered structures were investigated. The results of the theoretical calculations showed that the complexes could be forming a U-shaped geometry. However, the DFT calculations were performed for the isolated molecules in the gas phase at 0 K, and the thermotropic liquid crystals were enhanced in a molten state at a certain temperature range; conformational disorder could appear and strong deviations from the U-shape deduced from calculations could be impacted. Moreover, the actual confirmations in condensed phases could be very different, where the interaction as well as the electronic nature of the surrounding molecules could affect the geometrical structure. The geometry of the complexes was planar, where phenyl rings of the base and the acids were in the same plane. Recently, our group reported that [76] the molecular geometry of the H-bonded complexes might highly influence a certain mesophase behavior. The terminal intermolecular aggregations resulted from the change of the conformation by introduction of the terminal alkoxy chains, which play an important role for mesophase enhancement. The competitive effect of this interaction due to the terminal chain aggregation and the carbonyl ester, in addition to the lateral cohesive interactions, was highly impacted by the length of the terminal alkoxy chain. Moreover, increasing the core length (especially for complex I/III) and the number of side chains helped to induce mesophase formation. Furthermore, it widened the temperature range of the observed mesophase; this was clear in the phase transitions of I/III (Table 2). In our present work, these supramolecular complexes showed a nonlinear (U-shape) geometry which estimated DFT theoretical calculations. The calculated thermal variables, dipole moments and polarizability of both estimated U-shaped structures of SMHBCs I/II and I/III were illustrated in terms of the experimental data of the investigated mesophase, type and stability. The findings could be clarified in terms of the Π-Π aromatic stacking and the association of the flexible alkoxy chains. In general, the effective staking of the aromatic rings could be stabilizing the structure more than the aggregation of the terminals. The pronounced terminal interaction could be a good clarification for the observed nematic mesophase rather than the lateral interaction that enhances the smectic phase (Figure 3).
The predicted data of the DFT theoretical calculations for thermal variables, the polarizability and dipole moment of the individual compounds Ia, Ib, II, III and their supramolecular complexes I/II and I/III are tabulated in Table 3. As shown from Table 3, the stability of the base was dependent on the orientation of the N-atom with respect to the direction of the N=N bond, where the conformer Ia showed more stability than Ib. Moreover, the H-bonded formation of the complex enhanced the calculated thermal energy. The number of aromatic rings of the carboxylic acid affected the stability of the H-bonding complexes, where, as the number of aromatic rings increased the packing of the molecules by stacking of the aromatic rings increased, and this resulted in an increment in the thermodynamic stability of the molecules [63,66,67,76,77,78,79]. It is noteworthy that there was no effect of the H-bond formation on the dipole moment. However, the polarizability of the investigated compound was highly affected by the H-bond formation 318, 182 and 318 for the individual base I and acids II and III, respectively, and increased to 565, 706 Bohr3 for the H-bonded complexes I/II and I/III. The high polarizability of the complex could be predicted to have the best characteristics in nonlinear optics (NLO) applications.

3.4. Frontier Molecular Orbitals and Molecular Electrostatic Potential

The projected ground state isodensity surface projection for the FMOs, HOMO and LUMO, as well as their energies difference (ΔE) of I, II and III and their supramolecular complexes I/II and I/III are shown in Figure 4. Many parameters such as chemical hardness (η) and the global softness (S) might be calculated from the energy gap between HOMO and LUMO of I, II, III, I/II and I/III. These values were calculated as follow:
The hardness:
(η) = (I − A)/2
The global softness:
(S) = 1/ΔE
where I is the ionization energy and A is the electron affinity, (I − A) = (ELUMO − EHOMO).
The predicted softness estimated the aptitude of the π electron cloud of more the polarizable compound to be distorted by any interruption during by any chemical reaction associated with an electronic transportation. However, hard less polarizable compounds are rigid enough to resist transfer of electrons. As shown from Table 4, the FMO energy difference and the global softness (S) chemical hardness (η) were significantly affected by the H-bond formation of the complexes I/II and I/III. The H-bond formation between the acid and the base decreased the energy difference between FMOs (HOMO and LUMO), ΔE = 85.97, 117.34 and 79.07 kcal/mol for the base and acids, respectively; however, it decreased to 73.42 and 67.77 kcal/mol under complex formation for I/II and I/III, respectively. Moreover, the formation of the complex increased the global softness to 0.014 and 0.015 for I/II and I/III instead of 0.012, 0.009 and 0.013 for the base I and acids II and III, respectively. Moreover, the presence of the extra-conjugation of the azo group N=N of the acid III increased the global softness of the H-bonded complex.
The charge distribution map for I, II and III and their supramolecular complex I/II and I/III was predicted according to the molecular electrostatic potential (MEP) under the same basis sets (Figure 5). For the negatively charged atomic sites, the red region was located over the aromatic rings and its maximum localized on the carbonyl oxygen of the H-bonded COOH, while alkoxy chains were the blue regions, the least negatively charged atomic sites. Figure 5 shows that there was a considerable impact of H-bond formation on the mapped charge distribution. Recently, our group showed the relation between the extent and orientation of the mapped charges and the degree of the lateral and terminal interactions [39,41,42,43,44,45,46,47,48,49,50]. Such interactions could be used to explain the reason for the variation of the type of the enhanced mesophase in terms of the competitive attractions between end-to-end and side-to-side.

3.5. Refractive Index Measurements

An Abbe refractometer, from Bellingham, England, with a thermostat heating control unit within ±0.1 °C, was used to determine the refractive index at certain degrees of temperature. The compounds used were exposed to a He-Ne laser source of linearly polarized light (543 nm). The prisms of the Abbe refractometer were modulated for obtaining the planar and homeotropic alignment for measuring no and ne of the LC sample, respectively. The refractive indices no and ne for the compounds (I, II, I/II and I/III) were measured during the cooling process with an accuracy of ±0.0005, as in Figure 6, Figure 7, Figure 8 and Figure 9. It is obvious that as the temperature increased, the values of no increased with decrement in ne values. The sample III needs a high temperature to turn into the liquid crystalline phase, so that the Abbe refractometer cannot measure its refractive indices.
The effective geometry αeg parameter represents the spreading of light in the liquid crystals which can be obtained by the following equation [80]:
α e g = n o n e
Figure 10 shows that the values of αeg for compound I, II, I/II and I/III increased with increment in the temperature in the LC mesophase. At the isotropic phase, the αeg reached unity because of the lower molecular orientation ordering of the material.

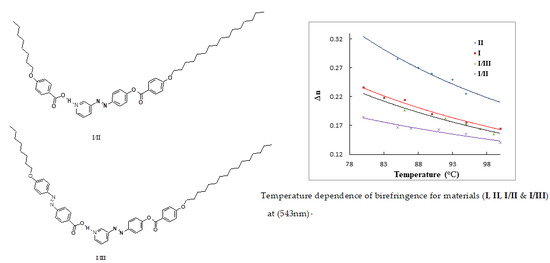
3.6. Birefringence Measurements

3.6.1. Measuring Birefringence by Using Abbe Refractometer

Birefringence Δn of the LC is one of the essential parameters for LCs, which affects the operation of the electro-optic devices [81,82,83]. Figure 11 shows the values of Δn = ne − no for the compounds I, II, I/II and I/III, which were obtained by measuring no and ne at a variable temperature by using a laser light source of wavelength (543 nm). It was noticed that as the temperature increased, the Δn values decreased gradually [81,82,83,84,85,86].
The values of birefringence for the individual compounds I and II were greater than that of the supramolecular complex I/II and I/III. The linear geometries of samples I and II caused an enhanced orientational director order, thus increasing the birefringence, while the nonlinear (U-shape) geometries of supramolecular complexes I/II and I/III (as shown in Figure 3) caused a decrement in the director order and birefringence. Additionally, the degree of packing of I/III was higher than that of I/II due to the long aromatic moiety of azo acid III with respect to the alkoxy acid II which caused a higher increase in the value of Δn for I/III than that of I/II, as shown in Figure 11. The values of Δn were plotted with the best fit in Figure 11, where the dots are the values calculated from the measured no and ne, and the solid line corresponds to the fitting of the curve using the relationship of dispersion of Cauchy.

3.6.2. Measuring Birefringence by Using Modified Spectrophotometer

Birefringence and the transition temperature for LC can be detected from the transmittance spectra during the processes of heating and cooling by using the modified spectrophotometer (MS) technique, as shown in Figure 12 [19,20]. The optical setup consists of diffraction grating (D), rotating disc (Sample, blank, shutter) (R), the mirror (M), the beam splitter (B), the polarizer and analyzer (P1 and P2), respectively, and the sample (S) was put into the electric oven with the unit of heating control rate 1 °C/min. Each sample was placed between two slices of the glass separated by four joints of 30 µm thickness in a uniform planar orientation with a parallel director to the cell walls. The edges of the LC cell were sealed with a heat resistant adhesive to avoid the leakage of the material during heating process. The sample cell in the electric oven was placed between two polarizers. The reference cell was also put between two polarizers, as shown in Figure 12. The intensity of the transmitted light was measured by the (MS) technique as a function of wavelength (200–800 nm) at certain temperatures for compounds I, II, I/II and I/III during heating and cooling temperatures.
Figure 13 indicates the difference in light transmittance at various temperatures with wavelength during the cooling process for the LC sample (I/II) as a representative sample of the data obtained, where the sample was placed between two crossed polarizers. This shape exhibited that the transmittance directly increased from 450 to 550 nm in wavelength and then became almost constant. The increasing transmittance during the LC phase was attributed to the orientational order of the mesogens. The phase transition was measured using the (MS) technique, and the results obtained were consistent with those measured by (DSC) and (POM) methods.
Birefringence (Δn) was calculated from the light transmittance of the sample in the LC phase as follows [22,23,34,35,36]:
Δ n = λ π t s i n − 1 T ⊥ ( λ ) T ‖ ( λ )
where T‖ and T⊥ are the transmission of light produced when the sample was placed between two parallel and crossed polarizers. The values of T⊥ and T‖ at such temperature and wavelength were measured for compounds I, II, I/II and I/III by using the (MS) technique. The sample thickness t was measured using a traveling microscope which was 30 µm. The values of Δn of compounds I, II, I/II and I/III in the LC phase under certain temperatures were measured by using a laser source of wavelength 543 nm, as listed in Table 5. These results are equal to the obtained values of Δn by using the Abbe refractometer within the error (±0.005) at the same wavelength and temperature degrees. The (MS) technique enabled us to measure the birefringence directly by knowing the transmission coefficients at different wavelengths.

3.7. Order Parameters Measurements

The phase transition in the liquid crystal at the transition point TC (the clearing temperature point) was accompanied with the emergence of some physical quantities such as microscopic and macroscopic order parameters. The microscopic order parameter S, which is responsible for the atomic displacement at the phase transition point TC, was calculated from the measured values of refractive indices (ne and no) of the LC compounds I, II, I/II and I/III by applying the hypothesis of Vuks as follows [87]:
S ( Δ α α ) = ( n e 2 − n o 2 ) 〈 n 2 〉 − 1
where α and Δα are the mean molecular polarizability and the anisotropy polarizability, respectively. The scaling factor Δα/α was obtained by using Haller’s extrapolation method, and by substituting in Equation (5), the order parameter S could be calculated for each sample [20,21,83]. Figure 14 shows the correlation between S and Δn for the compounds I, II, I/II and I/III, which was directly proportional.
In addition, the macroscopic order parameter can describe some physical properties such as polarization vector and elasticity of the mesogens in the liquid crystal phase. The macroscopic order parameter Q was related to the birefringence Δn and Δno in the LC and crystalline phase, respectively, as follows [28,29]:
Q = Δ n Δ n o
where the value of Δno (at T = 0 °C) can be obtained by using the Haller formula as follows [19,20,21,22,23,24,25,26]:
Δ n = Δ n o ( 1 − T T c ) β
TC is the transition point (the temperature transition from LC to the isotropic phase) and β is the material constant. From the relation between Δn and Ln(1−T/TC), the values of Δno and β were obtained for all samples, as shown in Table 5. As shown in Figure 15, the correlation between Q and Δn appeared directly proportional for the compounds I, II, I/II and I/III.
It was noted that the values of S and Q for the samples I/II and I were greater than those for the compounds I/III and II. This behavior may be attributed to the fact that TC for I/II and I was measured at the transition from the Smectic to isotropic phase, while for I/III and II, TC was measured at the transition from the nematic to isotropic phase, which changed the results for the different orientational order parameters for each compound.
It is well known that the mesomorphic and optical activities for certain liquid crystalline compounds depend mainly on mesomeric properties, intermolecular interactions and the stereo conformation of the molecule. In our present study, supramolecular H-bonded complexes, I/II and I/III, the association of the angular molecules and consequently, their mesophases stabilities depend mainly on several factors, namely: 1. Lateral adhesions of molecules that increase with the alkoxy-chain length. 2. Molecular geometry which varies according the planarity of complexes. 3. The steric effects. 4. End-to-end interaction that varies according to the polarity of the terminals and consequently, the polarizability of the whole complex. Comparing the thermal stabilities of prepared SMHBCs (I/II and I/III) indicates that all of these parameters (polarity, polarizability, coplanarity), do not have similar effects on the mesomorphic and optical behavior in these investigated complexes.

4. Conclusions

Mesomorphic and optical characterizations were carried out by DSC and polarized optical microscopy (POM) for the compounds I, II and their mixtures (I/II and I/III). The theoretical calculations were performed by the DFT method to predict the geometrical conformation for the present complexes as well as their thermal parameters. Computational calculation results revealed that the H-bonded complexes were of an angular structural shape. Ordinary and extraordinary refractive indices were determined by using the Abbe refractometer technique at different temperatures in the LC phase. Birefringence was also calculated from the difference between the measured data of ne and no and from the transmittance of light at the LC phase of each sample between two crossed and parallel polarizers by using a modified spectrophotometer. The values of birefringence for the individual compounds I and II are greater than that of the supramolecular complex I/II and I/III because of the higher planarity of the individual compounds than that of the coplanar supramolecular complex. Additionally, the values of Δn for I/III were higher than that for I/II due to the long aromatic moiety of azo acid III with respect to the alkoxy acid II, which affects their degree of packing ability. In spite of the higher phase transition temperature decreases for supramolecular complexes than individual compounds, birefringence decreases also. The values of birefringence for the individual compounds I and II are greater than that of the supramolecular complexes I/II and I/III because of the nonlinear (U-shape) geometrical structure of the supramolecular H-bonded complexes. Microscopic and macroscopic order parameters were determined at different temperatures and briefly discussed. Finally, the polarity, polarizability and coplanarity estimated parameters from DFT calculations do not have similar effects on the mesomorphic and optical behavior of the investigated supramolecular complexes.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4352/10/8/701/s1, Figure S1: DSC thermograms of 1:1 SMHBCs (a) I/II and (b) I/III at heating rate 10 °C/min upon heating and cooling cycles.

Author Contributions

Data curation, H.A.A., M.H. and A.A.Z.; formal analysis, H.A.A., and O.A.A.; funding acquisition, H.A.A., M.H. and O.A.A.; investigation, H.A.A., M.H. and A.A.Z. and O.A.A.; methodology, H.A.A., A.A.Z.; project administration, M.H. and A.A.Z.; resources, H.A.A., and O.A.A.; software, M.H.; supervision, H.A.A., M.H. and A.Z.; writing—original draft, H.A.A., M.H., A.Z. and O.A.A.; writing—review and editing, H.A.A., M.H. and A.A.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. De Gennes, P.-G.; Prost, J. The Physics of Liquid Crystals; Oxford University Press: Oxford, UK, 1993; Volume 83. [Google Scholar]
  2. Chandrasekhar, S. Liquid Crystals; Cambridge University Press: Cambridge, UK; New York, NY, USA, 1994; Volume 49, pp. 587–588. [Google Scholar]
  3. Priestly, E. Introduction to Liquid Crystals; Springer: Berlin, Germany, 2012. [Google Scholar]
  4. Aleksandriiskii, V.; Novikov, I.; Kuvshinova, S.; Burmistrov, V.; Koifman, O. Dielectric, optical and orientational properties of liquid crystalline 4-alkyloxy-4′-cyanoazoxybenzenes and 4-alkyloxy-4′-cyanoazobenzenes. J. Mol. Liq. 2016, 223, 1270–1276. [Google Scholar] [CrossRef]
  5. Gray, G.W.; Vill, V.; Spiess, H.W.; Demus, D.; Goodby, J.W. Physical Properties of Liquid Crystals; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
  6. Wilhelm, E.; Letcher, T. Heat Capacities: Liquids, Solutions and Vapours; Royal Society of Chemistry: London, UK, 2010. [Google Scholar]
  7. Nalwa, H.S. Handbook of Low and High Dielectric Constant Materials and Their Applications, Two-Volume Set; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
  8. Kumar, S. Experimental Study of Physical Properties and Phase Transitions; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
  9. Gramsbergen, E.F.; de Jeu, W.H. First-and second-order smectic-A to nematic phase transitions in p, p′-dialkylazoxybenzenes studied by birefringence. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1988, 84, 1015–1021. [Google Scholar] [CrossRef]
  10. Nesrullajev, A. Texture transformations and thermo-optical properties of nematic mesogen at nematic–isotropic liquid phase transition. J. Mol. Liq. 2014, 196, 217–222. [Google Scholar] [CrossRef]
  11. Zaki, A. Optical measurements of mixture thermotropic liquid crystals. Opt. Lasers Eng. 2010, 48, 538–542. [Google Scholar] [CrossRef]
  12. El-Dessouki, T.A.; Roushdy, M.; Hendawy, N.I.; Naoum, M.M.; Zaki, A.A. Optical measurements of thermotropic liquid crystals. J. Mod. Phys. 2013, 4, 39. [Google Scholar] [CrossRef] [Green Version]
  13. Zaki, A.A. Optical measurements and Speckle Photography for thermotropic liquid crystals Mixtures. J. Mod. Phys. 2013, 4, 517. [Google Scholar] [CrossRef] [Green Version]
  14. Miszczykd, E.; Pieceka, W. Application of modified interference wedge method in measurements of indices of refraction and birefringence of nematic liquid crystals. Acta Phys. Pol. A 2013, 124, 946–948. [Google Scholar]
  15. Okumuş, M.; Özgan, Ş.; Kırık, İ.; Kerli, S. Thermal and optical characterization of liquid crystal 4′-hexyl-4-biphenylcarbonitrile/4-hexylbenzoic acid mixtures. J. Mol. Struct. 2016, 1120, 150–155. [Google Scholar] [CrossRef]
  16. Devi, T.; Choudhury, B.; Bhattacharjee, A.; Dabrowski, R. Study of optical parameters of two fluorinated isothiocyanato nematic liquid crystals exhibiting high birefringence. Opto-Electron. Rev. 2014, 22, 24–30. [Google Scholar] [CrossRef]
  17. Thingujam, K.; Bhattacharjee, A.; Choudhury, B.; Dabrowski, R. Nematic liquid crystals exhibiting high birefringence. Opt. Rev. 2016, 23, 409–419. [Google Scholar] [CrossRef]
  18. Dąbrowski, R.; Kula, P.; Herman, J. High birefringence liquid crystals. Crystals 2013, 3, 443–482. [Google Scholar] [CrossRef]
  19. Zaki, A.A.; Ahmed, H.; Hagar, M. Impact of fluorine orientation on the optical properties of difluorophenylazophenyl benzoates liquid crystal. Mater. Chem. Phys. 2018, 216, 316–324. [Google Scholar] [CrossRef]
  20. Zaki, A. Optical measurements of phase transitions in difluorophenylazophenyl benzoate thermotropic liquid crystal with specific orientated fluorine atoms. Phase Transit. 2019, 92, 135–148. [Google Scholar] [CrossRef]
  21. Shen, P.; Zhang, X.; Lu, H.; Su, Z.; Zhou, Y.; Song, B.; Li, X.; Yang, X.; Tu, Y.; Li, C.Y. Effect of Fullerene Volume Fraction on Two-Dimensional Crystal-Constructed Supramolecular Liquid Crystals. Chem. Asian J. 2019, 14, 125–129. [Google Scholar] [CrossRef] [PubMed]
  22. Lehmann, M.; Dechant, M.; Gerbig, L.; Baumann, M. Supramolecular click procedures in liquid crystals. Liq. Cryst. 2019, 46, 1985–1994. [Google Scholar] [CrossRef]
  23. Saccone, M.; Pfletscher, M.; Kather, S.; Wölper, C.; Daniliuc, C.; Mezger, M.; Giese, M. Improving the mesomorphic behaviour of supramolecular liquid crystals by resonance-assisted hydrogen bonding. J. Mater. Chem. C 2019, 7, 8643–8648. [Google Scholar] [CrossRef]
  24. Sharma, V.S.; Shah, A.P.; Sharma, A.S. A new class of supramolecular liquid crystals derived from azo calix [4] arene functionalized 1, 3, 4-thiadiazole derivatives. New J. Chem. 2019, 43, 3556–3564. [Google Scholar] [CrossRef]
  25. Wang, X.; Bai, L.; Kong, S.; Song, Y.; Meng, F. Star-shaped supramolecular ionic liquid crystals based on pyridinium salts. Liq. Cryst. 2019, 46, 512–522. [Google Scholar] [CrossRef]
  26. Alhaddad, O.; Ahmed, H.; Hagar, M. Experimental and theoretical approaches of new nematogenic chair architectures of supramolecular H-bonded liquid crystals. Molecules 2020, 25, 365. [Google Scholar] [CrossRef] [Green Version]
  27. Ahmed, H.; Hagar, M.; Alhaddad, O. New chair shaped supramolecular complexes-based aryl nicotinate derivative; mesomorphic properties and DFT molecular geometry. RSC Adv. 2019, 9, 16366–16374. [Google Scholar] [CrossRef] [Green Version]
  28. Nafee, S.S.; Ahmed, H.A.; Hagar, M. New architectures of supramolecular H-bonded liquid crystal complexes based on dipyridine derivatives. Liq. Cryst. 2020, 1–14. [Google Scholar] [CrossRef]
  29. Alnoman, R.B.; Ahmed, H.A.; Hagar, M.; Abu Al-Ola, K.A.; Alrefay, B.S.; Haddad, B.A.; Albalawi, R.F.; Aljuhani, R.H.; Aloqebi, L.D.; Alsenani, S.F. Induced phases of new H-bonded supramolecular liquid crystal complexes; mesomorphic and geometrical estimation. Molecules 2020, 25, 1549. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  30. Alnoman, R.B.; Hagar, M.; Ahmed, H.A.; Abu Al-Ola, K.A.; Naoum, M.M.; Al-Elati, F.; Abdullah Zaid, Y.; Alsharif, A.; Al-Juhani, Y.; Abulrhelh, A. Characterization of New H-Bonded Liquid Crystalline Complexes Based on Iminophenyl Nicotinate. Crystals 2020, 10, 499. [Google Scholar] [CrossRef]
  31. Alhaddad, O.A.; Abu Al-Ola, K.A.; Hagar, M.; Ahmed, H.A. Chair-and V-Shaped of H-bonded Supramolecular Complexes of Azophenyl Nicotinate Derivatives; Mesomorphic and DFT Molecular Geometry Aspects. Molecules 2020, 25, 1510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Gray, G.W.; Jones, B. The mesomorphic transition points of the para-normal-alkoxybenzoic acids-a correction. J. Chem. Soc. 1953, 4179–4180. [Google Scholar] [CrossRef]
  33. Kato, T.; Frechet, J.M. A new approach to mesophase stabilization through hydrogen bonding molecular interactions in binary mixtures. J. Am. Chem. Soc. 1989, 111, 8533–8534. [Google Scholar] [CrossRef]
  34. Kato, T.; Wilson, P.G.; Fujishima, A.; Fréchet, J.M. Hydrogen-bonded liquid crystals. A novel mesogen incorporating nonmesogenic 4, 4′-bipyridine through selective recognition between hydrogen bonding donor and acceptor. Chem. Lett. 1990, 19, 2003–2006. [Google Scholar] [CrossRef]
  35. Kato, T.; Frechet, J.M.; Wilson, P.G.; Saito, T.; Uryu, T.; Fujishima, A.; Jin, C.; Kaneuchi, F. Hydrogen-bonded liquid crystals. Novel mesogens incorporating nonmesogenic bipyridyl compounds through complexation between hydrogen-bond donor and acceptor moieties. Chem. Mater. 1993, 5, 1094–1100. [Google Scholar] [CrossRef]
  36. Kato, T.; Fréchet, J.M.J. Hydrogen bonding and the self-assembly of supramolecular liquid-crystalline materials. Macromol. Symp. 1995, 98, 311–326. [Google Scholar] [CrossRef]
  37. Kihara, H.; Kato, T.; Uryu, T.; Frechet, J.M. Supramolecular liquid-crystalline networks built by self-assembly of multifunctional hydrogen-bonding molecules. Chem. Mater. 1996, 8, 961–968. [Google Scholar] [CrossRef]
  38. Kihara, H.; Kato, T.; Uryu, T.; Frechet, J.M. Induction of a cholesteric phase via self-assembly in supramolecular networks built of non-mesomorphic molecular components. Liq. Cryst. 1998, 24, 413–418. [Google Scholar] [CrossRef]
  39. Chen, K.-Y. Crystal Structure, Hydrogen-Bonding Properties, and DFT Studies of 2-((2-(2-Hydroxyphenyl) benzo [d] thiazol-6-yl) methylene) malononitrile. Mol. Cryst. Liq. Cryst. 2015, 623, 285–296. [Google Scholar] [CrossRef]
  40. Garcia-Amorós, J.; Reig, M.; Cuadrado, A.; Ortega, M.; Nonell, S.; Velasco, D. A photoswitchable bis-azo derivative with a high temporal resolution. Chem. Commun. 2014, 50, 11462–11464. [Google Scholar] [CrossRef] [PubMed]
  41. Shoji, M.; Tanaka, F. Theoretical study of hydrogen-bonded supramolecular liquid crystals. Macromolecules 2002, 35, 7460–7472. [Google Scholar] [CrossRef]
  42. Sundaram, S.; Jayaprakasam, R.; Dhandapani, M.; Senthil, T.; Vijayakumar, V. Theoretical (DFT) and experimental studies on multiple hydrogen bonded liquid crystals comprising between aliphatic and aromatic acids. J. Mol. Liq. 2017, 243, 14–21. [Google Scholar] [CrossRef]
  43. Hagar, M.; Ahmed, H.; Alhaddadd, O. DFT Calculations and Mesophase Study of Coumarin Esters and Its Azoesters. Crystals 2018, 8, 359. [Google Scholar] [CrossRef] [Green Version]
  44. Hagar, M.; Soliman, S.M.; Ibid, F.; El Sayed, H. Quinazolin-4-yl-sulfanylacetyl-hydrazone derivatives; Synthesis, molecular structure and electronic properties. J. Mol. Struct. 2013, 1049, 177–188. [Google Scholar] [CrossRef]
  45. Soliman, S.M.; Hagar, M.; Ibid, F.; El Sayed, H. Experimental and theoretical spectroscopic studies, HOMO–LUMO, NBO analyses and thione–thiol tautomerism of a new hybrid of 1, 3, 4-oxadiazole-thione with quinazolin-4-one. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 145, 270–279. [Google Scholar] [CrossRef]
  46. Hagar, M.; Soliman, S.M.; Ibid, F.; El Sayed, H. Synthesis, molecular structure and spectroscopic studies of some new quinazolin-4 (3H)-one derivatives; an account on the N-versus S-Alkylation. J. Mol. Struct. 2016, 1108, 667–679. [Google Scholar] [CrossRef]
  47. Aboelnaga, A.; Hagar, M.; Soliman, S.M. Ultrasonic Synthesis, Molecular Structure and Mechanistic Study of 1, 3-Dipolar Cycloaddition Reaction of 1-Alkynylpyridinium-3-olate and Acetylene Derivatives. Molecules 2016, 21, 848. [Google Scholar] [CrossRef] [Green Version]
  48. Ahmed, H.A.; Hagar, M.; El-Sayed, T.H.; Alnoman, R.B. Schiff base/ester liquid crystals with different lateral substituents: Mesophase behaviour and DFT calculations. Liq. Cryst. 2019, 46, 1–11. [Google Scholar] [CrossRef]
  49. Paterson, D.A.; Gao, M.; Kim, Y.-K.; Jamali, A.; Finley, K.L.; Robles-Hernández, B.; Diez-Berart, S.; Salud, J.; de la Fuente, M.R.; Timimi, B.A. Understanding the twist-bend nematic phase: The characterisation of 1-(4-cyanobiphenyl-4′-yloxy)-6-(4-cyanobiphenyl-4′-yl) hexane (CB6OCB) and comparison with CB7CB. Soft Matter 2016, 12, 6827–6840. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Martinez-Felipe, A.; Cook, A.G.; Abberley, J.P.; Walker, R.; Storey, J.M.; Imrie, C.T. An FT-IR spectroscopic study of the role of hydrogen bonding in the formation of liquid crystallinity for mixtures containing bipyridines and 4-pentoxybenzoic acid. RSC Adv. 2016, 6, 108164–108179. [Google Scholar] [CrossRef] [Green Version]
  51. Chen, R.; An, Z.; Wang, W.; Chen, X.; Chen, P. Lateral substituent effects on UV stability of high-birefringence liquid crystals with the diaryl-diacetylene core: DFT/TD-DFT study. Liq. Cryst. 2017, 44, 1515–1524. [Google Scholar] [CrossRef]
  52. Hagar, M.; Ahmed, H.; Saad, G. New calamitic thermotropic liquid crystals of 2-hydroxypyridine ester mesogenic core: Mesophase behaviour and DFT calculations. Liq. Cryst. 2020, 47, 114–124. [Google Scholar] [CrossRef]
  53. Nafee, S.S.; Ahmed, H.; Hagar, M. Theoretical, experimental and optical study of new thiophene-based liquid crystals and their positional isomers. Liq. Cryst. 2020, 1–12. [Google Scholar] [CrossRef]
  54. Nafee, S.S.; Hagar, M.; Ahmed, H.A.; El-Shishtawy, R.M.; Raffah, B.M. The synthesis of new thermal stable schiff base/ester liquid crystals: A computational, mesomorphic, and optical study. Molecules 2019, 24, 3032. [Google Scholar] [CrossRef] [Green Version]
  55. Alnoman, R.; Ahmed, H.A.; Hagar, M. Synthesis, optical, and geometrical approaches of new natural fatty acids’ esters/Schiff base liquid crystals. Molecules 2019, 24, 4293. [Google Scholar] [CrossRef] [Green Version]
  56. Ahmed, H.; Hagar, M.; Alhaddad, O. Mesomorphic and geometrical orientation study of the relative position of fluorine atom in some thermotropic liquid crystal systems. Liq. Cryst. 2019, 47, 404–413. [Google Scholar] [CrossRef]
  57. Alhaddad, O.A.; Ahmed, H.A.; Hagar, M.; Saad, G.R.; Abu Al-Ola, K.A.; Naoum, M.M. Thermal and photophysical studies of binary mixtures of liquid crystal with different geometrical mesogens. Crystals 2020, 10, 223. [Google Scholar] [CrossRef] [Green Version]
  58. Alnoman, R.B.; Hagar, M.; Ahmed, H.A.; Naoum, M.M.; Sobaih, H.A.; Almshaly, J.S.; Haddad, M.M.; Alhaisoni, R.A.; Alsobhi, T.A. Binary Liquid Crystal Mixtures Based on Schiff Base Derivatives with Oriented Lateral Substituents. Crystals 2020, 10, 319. [Google Scholar] [CrossRef]
  59. Hagar, M.; Ahmed, H.A.; Aljohani, G.; Alhaddad, O.A. Investigation of Some Antiviral N-Heterocycles as COVID 19 Drug: Molecular Docking and DFT Calculations. Int. J. Mol. Sci. 2020, 21, 3922. [Google Scholar] [CrossRef] [PubMed]
  60. Ahmed, H.A.; Mansour, E.; Hagar, M. Mesomorphic study and DFT simulation of calamitic Schiff base liquid crystals with electronically different terminal groups and their binary mixtures. Liq. Cryst. 2020, 1–13. [Google Scholar] [CrossRef]
  61. Hagar, M.; Ahmed, H.A.; Aouad, M.R. Mesomorphic and DFT diversity of Schiff base derivatives bearing protruded methoxy groups. Liq. Cryst. 2020, 1–12. [Google Scholar] [CrossRef]
  62. Naoum, M.M.; Fahmi, A.A.; Mohammady, S.Z.; Abaza, A.H. Effect of lateral substitution on supramolecular liquid crystal associates induced by hydrogen-bonding interactions between 4-(4′-pyridylazo-3-methylphenyl)-4′′-alkoxy benzoates and 4-substituted benzoic acids. Liq. Cryst. 2010, 37, 475–486. [Google Scholar] [CrossRef]
  63. Hagar, M.; Ahmed, H.; Alhaddad, O. Experimental and theoretical approaches of molecular geometry and mesophase behaviour relationship of laterally substituted azopyridines. Liq. Cryst. 2019, 46, 1440–1451. [Google Scholar] [CrossRef]
  64. Naoum, M.M.; Fahmi, A.A.; Refaie, A.A.; Alaasar, M.A. Novel hydrogen-bonded angular supramolecular liquid crystals. Liq. Cryst. 2012, 39, 47–61. [Google Scholar] [CrossRef]
  65. Ahmed, H.; Naoum, M. Mesophase behaviour of azobenzene-based angular supramolecular hydrogen-bonded liquid crystals. Liq. Cryst. 2016, 43, 222–234. [Google Scholar] [CrossRef]
  66. Ahmed, H.; Hagar, M.; Alaasar, M.; Naoum, M. Wide nematic phases induced by hydrogen-bonding. Liq. Cryst. 2018, 46, 550–559. [Google Scholar] [CrossRef]
  67. Hagar, M.; Ahmed, H.; Alhaddad, O. New azobenzene-based natural fatty acid liquid crystals with low melting point: Synthesis, DFT calculations and binary mixtures. Liq. Cryst. 2019, 46, 2223–2234. [Google Scholar] [CrossRef]
  68. Ahmed, H.; Hagar, M.; Aljuhani, A. Mesophase behavior of new linear supramolecular hydrogen-bonding complexes. Rsc. Adv. 2018, 8, 34937–34946. [Google Scholar] [CrossRef] [Green Version]
  69. Cleland, W.; Kreevoy, M.M. Low-barrier hydrogen bonds and enzymic catalysis. Science 1994, 264, 1887–1890. [Google Scholar] [CrossRef] [PubMed]
  70. Lizu, M.; Lutfor, M.; Surugau, N.; How, S.; Arshad, S.E. Synthesis and characterization of ethyl cellulose–based liquid crystals containing azobenzene chromophores. Mol. Cryst. Liq. Cryst. 2010, 528, 64–73. [Google Scholar] [CrossRef]
  71. Martínez-Felipe, A.; Imrie, C.T. The role of hydrogen bonding in the phase behaviour of supramolecular liquid crystal dimers. J. Mol. Struct. 2015, 1100, 429–437. [Google Scholar] [CrossRef]
  72. Ghanem, A.; Noel, C. FTIR investigation of two alkyl-p-terphenyl-4, 4″-dicarboxylates in their crystalline, smectic and isotropic phases. Mol. Cryst. Liq. Cryst. 1987, 150, 447–472. [Google Scholar] [CrossRef]
  73. Paterson, D.A.; Martínez-Felipe, A.; Jansze, S.M.; Marcelis, A.T.; Storey, J.M.; Imrie, C.T. New insights into the liquid crystal behaviour of hydrogen-bonded mixtures provided by temperature-dependent FTIR spectroscopy. Liq. Cryst. 2015, 42, 928–939. [Google Scholar] [CrossRef]
  74. Walker, R.; Pociecha, D.; Abberley, J.; Martinez-Felipe, A.; Paterson, D.; Forsyth, E.; Lawrence, G.; Henderson, P.; Storey, J.; Gorecka, E. Spontaneous chirality through mixing achiral components: A twist-bend nematic phase driven by hydrogen-bonding between unlike components. Chem. Commun. 2018, 54, 3383–3386. [Google Scholar] [CrossRef]
  75. Ahmed, H.; Naoum, M.; Saad, G. Mesophase behaviour of 1: 1 mixtures of 4-n-alkoxyphenylazo benzoic acids bearing terminal alkoxy groups of different chain lengths. Liq. Cryst. 2016, 43, 1259–1267. [Google Scholar] [CrossRef]
  76. Hagar, M.; Ahmed, H.; Saad, G. Synthesis and mesophase behaviour of Schiff base/ester 4-(arylideneamino) phenyl-4″-alkoxy benzoates and their binary mixtures. J. Mol. Liq. 2019, 273, 266–273. [Google Scholar] [CrossRef]
  77. Liu, Y.; Zhan, G.; Zhong, X.; Yua, Y.; Ganb, W. Effect of pi–pi stacking on the self-assembly of azomethine-type rod–coil liquid crystals. Liq. Cryst. 2011, 38, 995–1006. [Google Scholar] [CrossRef]
  78. Ahmed, H.; Hagar, M.; Saad, G. Impact of the proportionation of dialkoxy chain length on the mesophase behaviour of Schiff base/ester liquid crystals; experimental and theoretical study. Liq. Cryst. 2019, 46, 1611–1620. [Google Scholar] [CrossRef]
  79. Hagar, M.; Ahmed, H.; El-Sayed, T.; Alnoman, R. Mesophase behavior and DFT conformational analysis of new symmetrical diester chalcone liquid crystals. J. Mol. Liq. 2019, 285, 96–105. [Google Scholar] [CrossRef]
  80. Sreeramakavacham, S.S.; Rao, B.G.S.; Mallika, K.; Kumari, T.V.; Lakshminarayana, S.; Ha, S.T. Novel method for order parameter of ferroelectric liquid crystals by image analysis. Liq. Cryst. 2013, 40, 384–390. [Google Scholar] [CrossRef]
  81. Wu, S.-T.; Hsu, C.-S.; Shyu, K.-F. High birefringence and wide nematic range bis-tolane liquid crystals. Appl. Phys. Lett. 1999, 74, 344–346. [Google Scholar] [CrossRef] [Green Version]
  82. Haller, I. Thermodynamic and static properties of liquid crystals. Prog. Solid State Chem. 1975, 10, 103–118. [Google Scholar] [CrossRef]
  83. Patari, S.; Chakraborty, S.; Nath, A. The optical anisotropy and orientational order parameter of two mesogens having slightly different flexible side chain–a comparative study. Liq. Cryst. 2016, 43, 1017–1027. [Google Scholar] [CrossRef]
  84. Sastry, S.S.; Kumari, T.V.; Mallika, K.; Rao, B.G.S.; Ha, S.-T.; Lakshminarayana, S. Order parameter studies on EPAP alkanoate mesogens. Liq. Cryst. 2012, 39, 295–301. [Google Scholar] [CrossRef]
  85. Kumar, A. Determination of orientational order and effective geometry parameter from refractive indices of some nematics. Liq. Cryst. 2013, 40, 503–510. [Google Scholar] [CrossRef]
  86. Erkan, S.; Cetinkaya, M.; Yildiz, S.; Özbek, H. Critical behavior of a nonpolar smectogen from high-resolution birefringence measurements. Phys. Rev. E 2012, 86, 041705. [Google Scholar] [CrossRef]
  87. Li, J.; Wen, C.-H.; Gauza, S.; Lu, R.; Wu, S.-T. Refractive indices of liquid crystals for display applications. J. Disp. Technol. 2005, 1, 51. [Google Scholar] [CrossRef]
Crystals 10 00701 sch001 550
Scheme 1. 1:1 SMHB complexes (a) I/II and (b) I/III.
Scheme 1. 1:1 SMHB complexes (a) I/II and (b) I/III.
Crystals 10 00701 sch001
Crystals 10 00701 sch002a 550Crystals 10 00701 sch002b 550
Scheme 2. Preparation of 1:1 SMHB complexes (a) I/II and (b) I/III.
Scheme 2. Preparation of 1:1 SMHB complexes (a) I/II and (b) I/III.
Crystals 10 00701 sch002aCrystals 10 00701 sch002b
Crystals 10 00701 g001 550
Figure 1. FT-IR spectrum of azopyridine base I, acids II and III, as well as their 1:1 supramolecular H-bonded complex I/II and I/III.
Figure 1. FT-IR spectrum of azopyridine base I, acids II and III, as well as their 1:1 supramolecular H-bonded complex I/II and I/III.
Crystals 10 00701 g001
Crystals 10 00701 g002 550
Figure 2. Optical photomicrographs of compounds I and II and their complexes I/II and I/III upon heating.
Figure 2. Optical photomicrographs of compounds I and II and their complexes I/II and I/III upon heating.
Crystals 10 00701 g002
Crystals 10 00701 g003 550
Figure 3. Optimized geometrical structures of the base I ((a) Ia and (b) Ib), acids (c) II and (d) III and their supramolecular complex (e) I/II and (f) I/III; (●) C-atom; (●) O-atom; (●) N-atom.
Figure 3. Optimized geometrical structures of the base I ((a) Ia and (b) Ib), acids (c) II and (d) III and their supramolecular complex (e) I/II and (f) I/III; (●) C-atom; (●) O-atom; (●) N-atom.
Crystals 10 00701 g003
Crystals 10 00701 g004 550
Figure 4. The calculated ground state isodensity surface plots for frontier molecular orbitals of (a) base I, acids (b) II and (c) III and their supramolecular complexes (d) I/II and (e) I/III; (●) C-atom; (●) O-atom; (●) N-atom.
Figure 4. The calculated ground state isodensity surface plots for frontier molecular orbitals of (a) base I, acids (b) II and (c) III and their supramolecular complexes (d) I/II and (e) I/III; (●) C-atom; (●) O-atom; (●) N-atom.
Crystals 10 00701 g004
Crystals 10 00701 g005 550
Figure 5. Molecular electrostatic potentials (MEP) of (a) base I, acids (b) II and (c) III and their supramolecular complexes (d) I/II and (e) I/III; High negatively charged atomic sites (the red region); low negatively charged atomic sites (the blue region).
Figure 5. Molecular electrostatic potentials (MEP) of (a) base I, acids (b) II and (c) III and their supramolecular complexes (d) I/II and (e) I/III; High negatively charged atomic sites (the red region); low negatively charged atomic sites (the blue region).
Crystals 10 00701 g005
Crystals 10 00701 g006 550
Figure 6. Dependence temperature of refractive indices (▪) no and (♦) ne for compound I at 543 nm.
Figure 6. Dependence temperature of refractive indices (▪) no and (♦) ne for compound I at 543 nm.
Crystals 10 00701 g006
Crystals 10 00701 g007 550
Figure 7. Dependence temperature of refractive indices (▪) no and (♦) ne for compound II at 543 nm.
Figure 7. Dependence temperature of refractive indices (▪) no and (♦) ne for compound II at 543 nm.
Crystals 10 00701 g007
Crystals 10 00701 g008 550
Figure 8. Dependence temperature of refractive indices (▪) no and (♦) ne for the complex I/II at 543 nm.
Figure 8. Dependence temperature of refractive indices (▪) no and (♦) ne for the complex I/II at 543 nm.
Crystals 10 00701 g008
Crystals 10 00701 g009 550
Figure 9. Dependence temperature of refractive indices (▪) no and (♦) ne for the complex I/III at 543 nm.
Figure 9. Dependence temperature of refractive indices (▪) no and (♦) ne for the complex I/III at 543 nm.
Crystals 10 00701 g009
Crystals 10 00701 g010 550
Figure 10. Effective geometry parameter αeg for materials (I, II, I/II and I/III) varies with temperatures.
Figure 10. Effective geometry parameter αeg for materials (I, II, I/II and I/III) varies with temperatures.
Crystals 10 00701 g010
Crystals 10 00701 g011 550
Figure 11. Temperature dependence of birefringence for materials I, II, I/II and I/III at 543 nm. The dots are the measurements of no and ne, and the solid line corresponds to the fitting by using Cauchy dispersion relation.
Figure 11. Temperature dependence of birefringence for materials I, II, I/II and I/III at 543 nm. The dots are the measurements of no and ne, and the solid line corresponds to the fitting by using Cauchy dispersion relation.
Crystals 10 00701 g011
Crystals 10 00701 g012 550
Figure 12. Optical set-up of the modified spectrophotometer (MS) technique for measuring the transmittance and phase transition of LC samples, with diffraction grating (D); rotating disk (R); mirror (M); beam splitter (B); two polarizers (P1 and P2); and the sample (S) inside electric oven.
Figure 12. Optical set-up of the modified spectrophotometer (MS) technique for measuring the transmittance and phase transition of LC samples, with diffraction grating (D); rotating disk (R); mirror (M); beam splitter (B); two polarizers (P1 and P2); and the sample (S) inside electric oven.
Crystals 10 00701 g012
Crystals 10 00701 g013 550
Figure 13. The variable wavelength transmittance for the complex I/II at such temperatures.
Figure 13. The variable wavelength transmittance for the complex I/II at such temperatures.
Crystals 10 00701 g013
Crystals 10 00701 g014 550
Figure 14. The variable of microscopic parameter (S) with birefringence (Δn) for all samples used.
Figure 14. The variable of microscopic parameter (S) with birefringence (Δn) for all samples used.
Crystals 10 00701 g014
Crystals 10 00701 g015 550
Figure 15. Variable of macroscopic parameter (Q) with birefringence (Δn) for all samples used.
Figure 15. Variable of macroscopic parameter (Q) with birefringence (Δn) for all samples used.
Crystals 10 00701 g015
Table
Table 1. The calculated bond length (Å) wave numbers (cm−1) of characteristic groups of the base I, acids II and III and their supramolecular complex I/II and I/III.
Table 1. The calculated bond length (Å) wave numbers (cm−1) of characteristic groups of the base I, acids II and III and their supramolecular complex I/II and I/III.
CompoundύOH (cm−1)O-H (Å)ύC=O (cm−1)C=O (Å)ύC=NPyr (cm−1)C=NPyr (Å)ύNr=NPyr (cm−1)N=NPyr (Å)ύH-bond (cm−1)H-Bond (Å)
I----1615.91.3471475.61.211--
II3662.60.9761691.91.238------
III3660.70.9761691.11.237--1475.81.282--
I/II2561.31.0321668.51.2511617.71.3481475.51.2812561.31.619
I/III2469.91.0381669.11.2501618.21.3481475.41.2822469.91.597
Table
Table 2. Phase transition temperatures (T, °C) and enthalpy of transition (∆H, kJ/mol) for the individual compounds (I, II and III) and their supramolecular complexes (I/II and I/III).
Table 2. Phase transition temperatures (T, °C) and enthalpy of transition (∆H, kJ/mol) for the individual compounds (I, II and III) and their supramolecular complexes (I/II and I/III).
SampleTCr-SmC∆HCr-SmCTCr-SmA∆HCr-SmATSmC-N∆HSmC-NTSmA-I∆HSmA-ITN-I∆HN-I
I--96.123.5--121.51.6--
II101.047.0--108.04.7--147.01.9
III147.055.6--241.07.9--262.53.2
I/II- 76.427.4- 104.61.5--
I/III91.846.0--137.07.2--198.73.5
Cr = solid crystal; N = nematic; SmA = smectic A; SmC = smectic C; I = isotropic.
Table
Table 3. Thermal parameters (Hartree/Particle) and dipole moment (Debye) of the base Ia and Ib, acids II and III and their supramolecular complex I/II and I/III.
Table 3. Thermal parameters (Hartree/Particle) and dipole moment (Debye) of the base Ia and Ib, acids II and III and their supramolecular complex I/II and I/III.
ParameterIaIbIIIIII/III/III
Ecorr0.740.730.350.441.081.17
ZPVE−1711.82−1711.82−810.17−1150.57−2522.02−2862.42
Etot−1711.78−1711.78−810.15−1150.54−2521.96−2862.35
H−1711.78−1711.78−810.15−1150.54−2521.96−2862.35
G−1711.91−1711.91−810.22−1150.63−2522.14−2862.55
Total Dipole Moment5.27.74.35.34.64.2
Polarizability α474.0473.3182.5318.2676.8820.2
ZPVE: sum of electronic and zero-point energies; Etot: sum of electronic and thermal energies; H: sum of electronic and thermal enthalpies; G: sums of electronic and thermal free energies.
Table
Table 4. Molecular orbital energies, hardness (η) and global softness (S) of base I, acids II and III and their supramolecular complex I/II and I/III.
Table 4. Molecular orbital energies, hardness (η) and global softness (S) of base I, acids II and III and their supramolecular complex I/II and I/III.
CompoundEHOMO (Kcal/mol)ELUMO (Kcal/mol)ΔE(ELUMO − EHOMO) (Kcal/mol)η= ΔE(ELUMO − EHOMO)/2S = 1/ΔE
I−149.97−64.0085.9742.980.012
II−151.86−34.51117.3458.670.009
III−143.70−64.6379.0739.530.013
I/II−142.44−69.0373.4236.710.014
I/III−137.42−69.6567.7733.890.015
Table
Table 5. The values of birefringence Δn (by using the MS technique at 543 nm), Δno and β constant for all compounds.
Table 5. The values of birefringence Δn (by using the MS technique at 543 nm), Δno and β constant for all compounds.
SampleΔn Temp. (100 °C)Δnoβ
I0.18 ± 0.050.350.12
II0.23 ± 0.050.550.32
I/II0.16 ± 0.050.210.02
I/III0.17 ± 0.050.380.34

Share and Cite

MDPI and ACS Style

Ahmed, H.A.; Hagar, M.; Alhaddad, O.A.; Zaki, A.A. Optical and Geometrical Characterizations of Non-Linear Supramolecular Liquid Crystal Complexes. Crystals 2020, 10, 701. https://doi.org/10.3390/cryst10080701

AMA Style

Ahmed HA, Hagar M, Alhaddad OA, Zaki AA. Optical and Geometrical Characterizations of Non-Linear Supramolecular Liquid Crystal Complexes. Crystals. 2020; 10(8):701. https://doi.org/10.3390/cryst10080701

Chicago/Turabian Style

Ahmed, Hoda A., Mohamed Hagar, Omaima A. Alhaddad, and Ayman A. Zaki. 2020. "Optical and Geometrical Characterizations of Non-Linear Supramolecular Liquid Crystal Complexes" Crystals 10, no. 8: 701. https://doi.org/10.3390/cryst10080701

APA Style

Ahmed, H. A., Hagar, M., Alhaddad, O. A., & Zaki, A. A. (2020). Optical and Geometrical Characterizations of Non-Linear Supramolecular Liquid Crystal Complexes. Crystals, 10(8), 701. https://doi.org/10.3390/cryst10080701

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop