Competitive Dye Adsorption-Desorption on the Isotropic Surface at the Early Stage of the Photoexcitation of Azo Dye-Doped Liquid Crystals
Abstract
:1. Introduction
2. Experiments
2.1. Materials and Methods
2.2. Analysis Mechanism
3. Results and Discussion
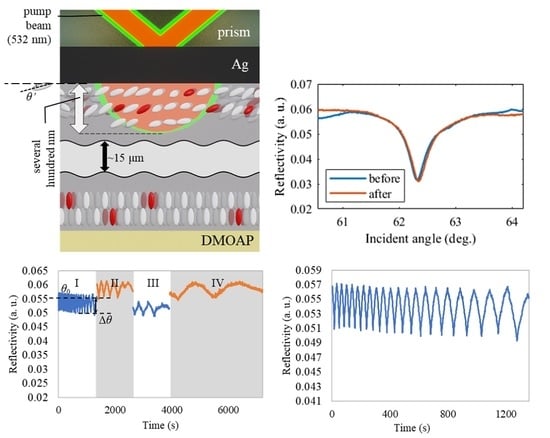
3.1. Vibration and Quick Response of LC
3.2. Evolution of Anchoring Caused by Dye-Adsorbed Layer via Photoexcitation
3.3. Adsorption and Desorption of Azo Dyes on Isotropic Surface
3.4. Depecdencies on Intensity
3.5. Source of Error—Thickness of the Adsorbed Layer
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bisoyi, H.K.; Li, Q. Light-Driven Liquid Crystalline Materials: From Photo-Induced Phase Transitions and Property Modulations to Applications. Chem. Rev. 2016, 116, 15089–15166. [Google Scholar] [CrossRef] [PubMed]
- Yaroshchuk, O.; Reznikov, Y. Photoalignment of liquid crystals: Basics and current trends. J. Mater. Chem. 2012, 22, 286–300. [Google Scholar] [CrossRef]
- Palomares, L.O.; Reyes, J.A.; Jánossy, I. Director reorientation in a nematic liquid crystal with a photosensitive layer. Phys. Rev. E 2014, 90, 062503. [Google Scholar] [CrossRef] [PubMed]
- Serak, S.; Bunning, T.; Tabiryan, N. Ultrafast Photoalignment: Recording a Lens in a Nanosecond. Crystals 2017, 7, 338. [Google Scholar] [CrossRef] [Green Version]
- Chigrinov, V.; Sun, J.; Wang, X. Photoaligning and Photopatterning: New LC Technology. Crystals 2020, 10, 323. [Google Scholar] [CrossRef] [Green Version]
- Nassrah, A.R.K.; Jánossy, I.; Tóth-Katona, T. Photoalignment at the nematic liquid crystal–polymer interface: The importance of the liquid crystalline molecular structure. J. Mol. Liq. 2020, 312, 113309. [Google Scholar] [CrossRef]
- Simoni, F.; Francescangeli, O. Effects of light on molecular orientation of liquid crystals. J. Phys. Condens. Matter 1999, 11, R439–R487. [Google Scholar] [CrossRef]
- Jánossy, I.; Szabados, L. Optical reorientation of nematic liquid crystals in the presence of photoisomerization. Phys. Rev. E 1998, 58, 4598–4604. [Google Scholar] [CrossRef] [Green Version]
- Francescangeli, O.; Slussarenko, S.; Simoni, F.; Andrienko, D.; Reshetnyak, V.; Reznikov, Y. Light-Induced Surface Sliding of the Nematic Director in Liquid Crystals. Phys. Rev. Lett. 1999, 82, 1855–1858. [Google Scholar] [CrossRef] [Green Version]
- Marusii, T.; Reznikov, Y.; Voloshchenko, D.; Reshetnyak, V. Surface Driven Orientation Effect in NLC Cell. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1994, 251, 209–218. [Google Scholar] [CrossRef]
- Anderle, K.; Wendorff, J.H. Holographic Recording, Using Liquid Crystalline Side Chain Polymers. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 1994, 243, 51–75. [Google Scholar] [CrossRef]
- Rau, H. Photoisomerization of azobenzenes. In Photochemistry and Photophysics; Jan, F.R., Gary, W.S., Eds.; CRC Press: Boca Raton, FL, USA, 1990; Volume 2, pp. 119–141. [Google Scholar]
- Ouskova, E.; Fedorenko, D.; Reznikov, Y.; Shiyanovskii, S.V.; Su, L.; West, J.L.; Kuksenok, O.V.; Francescangeli, O.; Simoni, F. Hidden photoalignment of liquid crystals in the isotropic phase. Phys. Rev. E 2001, 63, 021701. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lucchetti, L.; Difabrizio, M.; Francescangeli, O.; Simoni, F. Light-induced adsorption and desorption in dynamic and stable grating formation in methyl-red doped liquid crystals. J. Nonlinear Opt. Phys. Mater. 2002, 11, 13–23. [Google Scholar] [CrossRef]
- Fedorenko, D.; Ouskova, E.; Reshetnyak, V.; Reznikov, Y. Evolution of light-induced anchoring in dye-doped nematics: Experiment and model. Phys. Rev. E 2006, 73, 031701. [Google Scholar] [CrossRef]
- Lucchetti, L.; DiFabrizio, M.; Francescangeli, O.; Simoni, F. Colossal optical nonlinearity in dye doped liquid crystals. Opt. Commun. 2004, 233, 417–424. [Google Scholar] [CrossRef]
- Lucchetti, L.; Simoni, F. Light-induced adsorption and desorption in Methyl-Red-doped liquid crystals: A review. Liq. Cryst. Rev. 2015, 3, 79–98. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Lin, Y.-R.; Lo, K.-Y.; Lee, C.-R. Dynamics of photoalignment in azo-dye-doped liquid crystals. Appl. Phys. Lett. 2008, 93, 181114. [Google Scholar] [CrossRef] [Green Version]
- Eichler, H.J.; Macdonald, R. Flow-alignment and inertial effects in picosecond laser-induced reorientation phenomena of nematic liquid crystals. Phys. Rev. Lett. 1991, 67, 2666–2669. [Google Scholar] [CrossRef]
- Voloshchenko, D.; Khyzhnyak, A.; Reznikov, Y.; Reshetnyak, V. Control of an Easy-Axis on Nematic-Polymer Interface by Light Action to Nematic Bulk. Jpn. J. Appl. Phys. 1995, 34, 566–571. [Google Scholar] [CrossRef]
- Lo, K.-Y.; Huang, C.-Y. Observation of transient reorientation of dye-doped liquid crystals by pumped attenuated total reflection. Appl. Phys. Lett. 2006, 89, 081114. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Cheng, Z.-Z.; Lo, K.-Y.; Lee, C.-R. Determination of polar anchoring energy of dye-doped liquid crystals by measuring capacitance. J. Appl. Phys. 2010, 107, 123104. [Google Scholar] [CrossRef]
- Shinbo, K.; Ishikawa, J.; Baba, A.; Kaneko, F.; Kato, K.; Advincula, R.C. Alignments of Nematic Liquid Crystal Molecules on Azo-Dye-Containing Alternate Self-Assembled Films Investigated Using Attenuated Total Reflection Method. Jpn. J. Appl. Phys. 2002, 41, 2753–2758. [Google Scholar] [CrossRef]
- Lo, K.Y.; Huang, C.Y.; Chu, T.H.; Hsu, C.J.; Lin, C.H.; Fuh, A.Y.G. Variation of nematic liquid crystal on a silver surface. J. Opt. A Pure Appl. Opt. 2006, 8, 501–506. [Google Scholar] [CrossRef]
- Lo, K.Y.; Huang, C.Y. Dynamics of the photoexictation of azo dye-doped liquid crystals probing by pumped attenuated total reflection. In Proceedings of the Liquid Crystals and Applications in Optics, Prague, Czech Republic, 16 April 2007; Glogarova, M., Palffy-Muhoray, P., Copic, M., Eds.; SPIE: Bellingham, WA, USA; Volume 6587, p. 65870R. [Google Scholar] [CrossRef]
- Yakovlev, D.A.; Chigrinov, V.G.; Kwok, H.S. Modeling and Optimization of LCD Optical Performance; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Thomas, O.; Brogat, M. Organic Constituents. In UV-Visible Spectrophotometry of Water and Wastewater, 2nd ed.; Thomas, O., Burgess, C., Eds.; Elsevier: London, UK, 2017; pp. 73–138. ISBN 978-0-444-63897-700003-2. [Google Scholar]
- Heilmeier, G.H.; Zanoni, L.A. Guest-Host Interactions in Nematic Liquid Crystals. A New Electro-Optic Effect. Appl. Phys. Lett. 1968, 13, 91–92. [Google Scholar] [CrossRef]
- Józefowski, L.; Fiutowski, J.; Kawalec, T.; Rubahn, H.-G. Direct measurement of the evanescent-wave polarization state. J. Opt. Soc. Am. B 2007, 24, 624. [Google Scholar] [CrossRef] [Green Version]
- Barbero, G.; Durand, G. On the validity of the Rapini-Papoular surface anchoring energy form in nematic liquid crystals. J. Phys. 1986, 47, 2129–2134. [Google Scholar] [CrossRef]
- Lee, C.-R.; Fu, T.-L.; Cheng, K.-T.; Mo, T.-S.; Fuh, A.Y.-G. Surface-assisted photoalignment in dye-doped liquid-crystal films. Phys. Rev. E 2004, 69, 031704. [Google Scholar] [CrossRef] [Green Version]
- Saad, B.; Denariez-Roberge, M.M.; Galstyan, T.V. Diffusion of photoexcited azo dye in a liquid-crystal host. Opt. Lett. 1998, 23, 727. [Google Scholar] [CrossRef]
- Kuksenok, O.V.; Shiyanovskii, S.V. Surface Control of Dye Adsorption in Liquid Crystals. Mol. Cryst. Liq. Cryst. Sci. Technol. Sect. A Mol. Cryst. Liq. Cryst. 2001, 359, 107–118. [Google Scholar] [CrossRef]
- Lucchetti, L.; Simoni, F. Role of space charges on light-induced effects in nematic liquid crystals doped by methyl red. Phys. Rev. E 2014, 89, 032507. [Google Scholar] [CrossRef]





| Pump Laser Amplitude (mW) | Dip Angle α (°) | ||
|---|---|---|---|
| Before | After | Shift Δα | |
| 0.3 | 62.40 | 62.40 | 0.00 |
| 0.6 | 62.32 | 62.35 | 0.03 |
| 1.0 | 62.30 | 62.36 | 0.06 |
| 3.0 | 62.26 | 62.43 | 0.17 |
| 5.0 | 62.36 | 62.65 | 0.29 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.-T.; Ji, S.-C.; Chen, S.-H.; Huang, C.-Y.; Lo, K.Y. Competitive Dye Adsorption-Desorption on the Isotropic Surface at the Early Stage of the Photoexcitation of Azo Dye-Doped Liquid Crystals. Crystals 2020, 10, 802. https://doi.org/10.3390/cryst10090802
Chen W-T, Ji S-C, Chen S-H, Huang C-Y, Lo KY. Competitive Dye Adsorption-Desorption on the Isotropic Surface at the Early Stage of the Photoexcitation of Azo Dye-Doped Liquid Crystals. Crystals. 2020; 10(9):802. https://doi.org/10.3390/cryst10090802
Chicago/Turabian StyleChen, Wei-Ting, Sheng-Chung Ji, Shih-Hsuan Chen, Chia-Yi Huang, and Kuang Yao Lo. 2020. "Competitive Dye Adsorption-Desorption on the Isotropic Surface at the Early Stage of the Photoexcitation of Azo Dye-Doped Liquid Crystals" Crystals 10, no. 9: 802. https://doi.org/10.3390/cryst10090802
APA StyleChen, W. -T., Ji, S. -C., Chen, S. -H., Huang, C. -Y., & Lo, K. Y. (2020). Competitive Dye Adsorption-Desorption on the Isotropic Surface at the Early Stage of the Photoexcitation of Azo Dye-Doped Liquid Crystals. Crystals, 10(9), 802. https://doi.org/10.3390/cryst10090802