Molecular Dynamics Simulation in the Interlayer of Mixed-Layer Clays Due to Hydration and Swelling Mechanism
Abstract
:1. Introduction
2. Theoretical Calculations
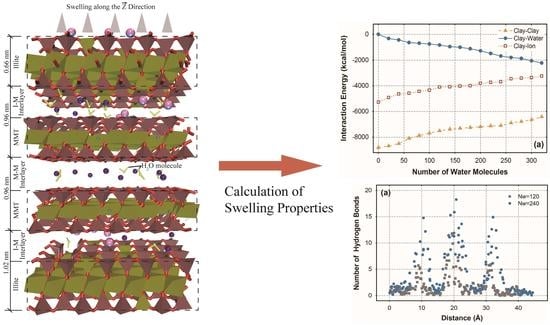
2.1. Molecular Model of Mixed-Layer Clay
2.2. Computational Details
2.2.1. Force Field
2.2.2. Simulation Procedure
2.3. Properties
2.3.1. Basal Spacing d
2.3.2. Interaction Energy
2.3.3. Calculation of Hydrogen Bonds
3. Results and Discussions
3.1. Hydration Swelling
3.2. Interaction Energy
3.3. Distribution of Hydrogen Bonds
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karaborni, S.; Smit, B.; Heidug, W.; Urai, J.; Van Oort, E. The swelling of clays: Molecular simulations of the hydration of montmorillonite. Science 1996, 271, 1102–1104. [Google Scholar] [CrossRef] [Green Version]
- Katti, D.R.; Srinivasamurthy, L.; Katti, K.S. Molecular modeling of initiation of interlayer swelling in Na–montmorillonite expansive clay. Can. Geotech. J. 2015, 52, 1385–1395. [Google Scholar] [CrossRef]
- Buzzi, O.; Fityus, S.; Sloan, S.W. Use of expanding polyurethane resin to remediate expansive soil foundations. Can. Geotech. J. 2010, 47, 623–634. [Google Scholar] [CrossRef] [Green Version]
- Anderson, R.L.; Ratcliffe, I.; Greenwell, H.C.; Williams, P.A.; Cliffe, S.; Coveney, P.V. Clay swelling—A challenge in the oilfield. Earth Sci. Rev. 2010, 98, 201–216. [Google Scholar] [CrossRef]
- Amarasinghe, P.M.; Katti, K.S.; Katti, D.R. Insight into role of clay-fluid molecular interactions on permeability and consolidation behavior of Na-montmorillonite swelling clay. J. Geotech. Geoenviron. Eng. 2012, 138, 138–146. [Google Scholar] [CrossRef]
- Brown, G.; MacEwan, D.M.C. The interpretation of X-ray diagrams of soil clays. II. Structures with random interstratification. J. Soil Sci. 1950, 1, 239–253. [Google Scholar] [CrossRef]
- Weaver, C.E. The Distribution and Identification of Mixed-layer Clays in Sedimentary Rocks1. Clays Clay Miner. 1955, 4, 385–386. [Google Scholar] [CrossRef]
- Altaner, S.P.; Ylagan, R.F. Comparison of structural models of mixed-layer illite/smectite and reaction mechanisms of smectite illitization. Clays Clay Miner. 1997, 45, 517–533. [Google Scholar] [CrossRef]
- Jo, H.Y.; Katsumi, T.; Benson, C.H.; Edil, T.B. Hydraulic conductivity and swelling of nonprehydrated GCLs permeated with single-species salt solutions. J. Geotech. Geoenviron. Eng. 2001, 127, 557–567. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the stability of lyophobic colloids. J. Colloid Sci. 1955, 10, 224–225. [Google Scholar] [CrossRef] [Green Version]
- Hurst, A. Geochemistry of Clay-Pore Fluid Interactions. Clay Miner. 1993, 28, 657–659. [Google Scholar] [CrossRef]
- Amarasinghe, P.M.; Katti, K.S.; Katti, D.R. Nature of organic fluid-montmorillonite interactions: An FTIR spectroscopic study. J. Colloid Interface Sci. 2009, 337, 97–105. [Google Scholar] [CrossRef]
- Katti, D.R.; Shanmugasundaram, V. Influence of swelling on the microstructure of expansive clays. Can. Geotech. J. 2001, 38, 175–182. [Google Scholar] [CrossRef]
- Underwood, T.; Erastova, V.; Greenwell, H.C. Ion adsorption at clay-mineral surfaces: The Hofmeister series for hydrated smectite minerals. Clays Clay Miner. 2016, 64, 472–487. [Google Scholar] [CrossRef] [Green Version]
- Diaz-Perez, A.; Cortes-Monroy, I.; Roegiers, J.C. The role of water/clay interaction in the shale characterization. J. Pet. Sci. Eng. 2007, 58, 83–98. [Google Scholar] [CrossRef]
- Marry, V.; Dubois, E.; Malikova, N.; Breu, J.; Haussler, W. Anisotropy of water dynamics in clays: Insights from molecular simulations for experimental QENS analysis. J. Phys. Chem. C 2013, 117, 15106–15115. [Google Scholar] [CrossRef]
- Rahromostaqim, M.; Sahimi, M. Molecular Dynamics Study of the Effect of Layer Charge and Interlayer Cations on Swelling of Mixed-Layer Chlorite–Montmorillonite Clays. J. Phys. Chem. C 2020, 124, 2553–2561. [Google Scholar] [CrossRef]
- Kalo, H.; Milius, W.; Breu, J. Single crystal structure refinement of one- and two-layer hydrates of sodium fluorohectorite. Z. Anorg. Allg. Chem. 2012, 2, 8452–8459. [Google Scholar] [CrossRef]
- Anderson, M.T.; Lu, N. Role of microscopic physicochemical forces in large volumetric strains for clay sediments. J. Eng. Mech. 2001, 127, 710–719. [Google Scholar] [CrossRef]
- Anandarajah, A. Mechanism controlling permeability change in clays due to changes in pore fluid. J. Geotech. Geoenviron. Eng. 2003, 129, 163–172. [Google Scholar] [CrossRef]
- Jeanmairet, G.; Marry, V.; Levesque, M.; Rotenberg, B.; Borgis, D. Hydration of clays at the molecular scale: The promising perspective of classical density functional theory. Mol. Phys. 2014, 112, 1320–1329. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Lu, X.; Wang, R.; Zhou, H. Effects of layer-charge distribution on the thermodynamic and microscopic properties of Cs-smectite. Geochim. Cosmochim. Acta 2008, 72, 1837–1847. [Google Scholar] [CrossRef]
- Ai, Y.; Zhao, C.; Sun, L.; Wang, X.; Liang, L. Coagulation mechanisms of humic acid in metal ions solution under different pH conditions: A molecular dynamics simulation. Sci. Total Environ. 2020, 702, 135072. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Z.; Deng, P. Using molecular dynamics to unravel phase composition behavior of nano-size pores in frozen soils: Does Young–Laplace equation apply in low temperature range? Can. Geotech. J. 2018, 55, 1144–1153. [Google Scholar] [CrossRef]
- Zhang, B.; Kang, J.; Kang, T. Effect of water on methane adsorption on the kaolinite (0 0 1) surface based on molecular simulations. Appl. Surf. Sci. 2018, 439, 792–800. [Google Scholar] [CrossRef]
- Yang, Y.; Adhikari, S.; Xu, G. Molecular simulation to discover rheological properties and soil-binding ability of PHPA polymer on montmorillonite surface. Surf. Interface Anal. 2020, 52, 665–675. [Google Scholar] [CrossRef]
- Hantal, G.; Brochard, L.; Laubie, H.; Ebrahimi, D.; Pellenq, R.J.M.; Ulm, F.J.; Coasne, B. Atomic-scale modelling of elastic and failure properties of clays. Mol. Phys. 2014, 112, 1294–1305. [Google Scholar] [CrossRef]
- Hensen, E.J.M.; Smit, B. Why clays swell. J. Phys. Chem. B 2002, 106, 12664–12667. [Google Scholar] [CrossRef] [Green Version]
- Lau, D.; Jian, W.; Yu, Z.; Hui, D. Nano-engineering of construction materials using molecular dynamics simulations: Prospects and challenges. Compos. Part B Eng. 2018, 143, 282–291. [Google Scholar] [CrossRef]
- Teich-McGoldrick, S.L.; Greathouse, J.A.; Jove-Colon, C.F.; Cygan, R.T. Swelling properties of montmorillonite and beidellite clay minerals from molecular simulation: Comparison of temperature, interlayer cation, and charge location effects. J. Phys. Chem. C 2015, 119, 20880–20891. [Google Scholar] [CrossRef]
- Rotenberg, B.; Marry, V.; Vuilleumier, R.; Malikova, N.; Simon, C.; Turq, P. Water and ions in clays: Unraveling the interlayer/micropore exchange using molecular dynamics. Geochim. Cosmochim. Acta 2007, 71, 5089–5101. [Google Scholar] [CrossRef]
- Rahromostaqim, M.; Sahimi, M. Molecular dynamics simulation of hydration and swelling of mixed-layer clays. J. Phys. Chem. C 2018, 122, 14631–14639. [Google Scholar] [CrossRef]
- Morrow, C.P.; Yazaydin, A.O.; Krishnan, M.; Bowers, G.M.; Kalinichev, A.G.; Kirkpatrick, R.J. Structure, energetics, and dynamics of smectite clay interlayer hydration: Molecular dynamics and metadynamics investigation of Na-hectorite. J. Phys. Chem. C 2013, 117, 5172–5187. [Google Scholar] [CrossRef] [Green Version]
- Asay, D.B.; Kim, S.H. Evolution of the adsorbed water layer structure on silicon oxide at room temperature. J. Phys. Chem. B 2005, 109, 16760–16763. [Google Scholar] [CrossRef]
- Reynolds, R.C.; Hower, J. The nature of interlayering in mixed-layer illite-montmorillonites. Clays Clay Miner. 1970, 18, 25–36. [Google Scholar] [CrossRef]
- Downs, R.T.; Hall-Wallace, M. The American Mineralogist crystal structure database. Am. Mineral. 2003, 88, 247–250. [Google Scholar]
- Viani, A.; Gualtieri, A.F.; Artioli, G. The nature of disorder in montmorillonite by simulation of X-ray powder patterns. Am. Mineral. 2002, 87, 966–975. [Google Scholar] [CrossRef]
- Carrier, B.; Wang, L.; Vandamme, M.; Pellenq, R.J.M.; Bornert, M.; Tanguy, A.; Van Damme, H. ESEM study of the humidity-induced swelling of clay film. Langmuir 2013, 29, 12823–12833. [Google Scholar] [CrossRef] [PubMed]
- Segad, M.; Jonsson, B.; Åkesson, T.; Cabane, B. Ca/Na montmorillonite: Structure, forces and swelling properties. Langmuir 2010, 26, 5782–5790. [Google Scholar] [CrossRef] [PubMed]
- Salles, F.; Douillard, J.M.; Bildstein, O.; Van Damme, H. Impact of the substitution distribution and the interlayer distance on both the surface energy and the hydration energy for Pb-montmorillonite. Appl. Clay Sci. 2011, 53, 379–385. [Google Scholar] [CrossRef] [Green Version]
- Salles, F.; Bildstein, O.; Douillard, J.M.; Jullien, M.; Raynal, J.; Van Damme, H. On the cation dependence of interlamellar and interparticular water and swelling in smectite clays. Langmuir 2010, 26, 5028–5037. [Google Scholar] [CrossRef] [PubMed]
- Cygan, R.T.; Liang, J.J.; Kalinichev, A.G. Molecular models of hydroxide, oxyhydroxide, and clay phases and the development of a general force field. J. Phys. Chem. B 2004, 108, 1255–1266. [Google Scholar] [CrossRef]
- Liu, X.; Lu, X.; Wang, R.; Zhou, H.; Xu, S. Molecular dynamics insight into the cointercalation of hexadecyltrimethyl-ammonium and acetate ions into smectites. Am. Mineral. 2009, 94, 143–150. [Google Scholar] [CrossRef]
- Carrier, B.; Vandamme, M.; Pellenq, R.J.M.; Van Damme, H. Elastic properties of swelling clay particles at finite temperature upon hydration. J. Phys. Chem. C 2014, 118, 8933–8943. [Google Scholar] [CrossRef]
- Neelov, A.; Holm, C. Interlaced P3M algorithm with analytical and ik-differentiation. J. Chem. Phys. 2010, 132, 234103. [Google Scholar] [CrossRef] [PubMed]
- Leimkuhler, B.; Noorizadeh, E.; Penrose, O. Comparing the efficiencies of stochastic isothermal molecular dynamics methods. J. Stat. Phys. 2011, 143, 921–942. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, X.; Liu, X.; Zhou, J.; Zhou, H. Hydration and mobility of interlayer ions of (Na X, Ca Y)-montmorillonite: A molecular dynamics study. J. Phys. Chem. C 2014, 118, 29811–29821. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, Y.L.; He, D.D.; Liu, G.S. Adsorption of cationic collectors and water on muscovite (0 0 1) surface: A molecular dynamics simulation study. Miner. Eng. 2013, 53, 101–107. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Hydrogen-bond kinetics in liquid water. Nature 1996, 379, 55–57. [Google Scholar] [CrossRef]
- Luzar, A.; Chandler, D. Effect of environment on hydrogen bond dynamics in liquid water. Phys. Rev. Lett. 1996, 76, 928. [Google Scholar] [CrossRef]
- Durrant, J.D.; McCammon, J.A. HBonanza: A computer algorithm for molecular-dynamics-trajectory hydrogen-bond analysis. J. Mol. Graph. Model. 2011, 31, 5–9. [Google Scholar] [CrossRef] [Green Version]
- Bowers, G.M.; Bish, D.L.; Kirkpatrick, R.J. H2O and cation structure and dynamics in expandable clays: 2H and 39K NMR investigations of hectorite. J. Phys. Chem. C 2008, 112, 6430–6438. [Google Scholar] [CrossRef]
- Ngouana, W.B.F.; Kalinichev, A.G. Structural arrangements of isomorphic substitutions in smectites: Molecular simulation of the swelling properties, interlayer structure, and dynamics of hydrated Cs–montmorillonite revisited with new clay models. J. Phys. Chem. C 2014, 118, 12758–12773. [Google Scholar] [CrossRef]
- Cases, J.M.; Bérend, I.; Besson, G.; Francois, M.; Uriot, J.P.; Thomas, F.; Poirier, J.E. Mechanism of adsorption and desorption of water vapor by homoionic montmorillonite. 1. The sodium-exchanged form. Langmuir 1992, 8, 2730–2739. [Google Scholar] [CrossRef]
- Lammers, L.N.; Bourg, I.C.; Okumura, M.; Kolluri, K.; Sposito, G.; Machida, M. Molecular dynamics simulations of cesium adsorption on illite nanoparticles. J. Colloid Interface Sci. 2017, 490, 608–620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.D.; Lu, X.C. A thermodynamic understanding of clay-swelling inhibition by potassium ions. Angew. Chem. Int. Ed. 2006, 45, 6300–6303. [Google Scholar] [CrossRef]
- Boek, E.S. Molecular dynamics simulations of interlayer structure and mobility in hydrated Li-, Na- and K-montmorillonite clays. Mol. Phys. 2014, 112, 1472–1483. [Google Scholar] [CrossRef]
- Pradhan, S.M.; Katti, K.S.; Katti, D.R. Evolution of molecular interactions in the interlayer of Na-montmorillonite swelling clay with increasing hydration. Int. J. Geomech. 2015, 15, 04014073. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Adhikari, S.; Xu, G. Molecular Dynamics Simulation in the Interlayer of Mixed-Layer Clays Due to Hydration and Swelling Mechanism. Crystals 2021, 11, 586. https://doi.org/10.3390/cryst11060586
Yang Y, Adhikari S, Xu G. Molecular Dynamics Simulation in the Interlayer of Mixed-Layer Clays Due to Hydration and Swelling Mechanism. Crystals. 2021; 11(6):586. https://doi.org/10.3390/cryst11060586
Chicago/Turabian StyleYang, Yu, Sanjeev Adhikari, and Guoyuan Xu. 2021. "Molecular Dynamics Simulation in the Interlayer of Mixed-Layer Clays Due to Hydration and Swelling Mechanism" Crystals 11, no. 6: 586. https://doi.org/10.3390/cryst11060586
APA StyleYang, Y., Adhikari, S., & Xu, G. (2021). Molecular Dynamics Simulation in the Interlayer of Mixed-Layer Clays Due to Hydration and Swelling Mechanism. Crystals, 11(6), 586. https://doi.org/10.3390/cryst11060586