Homogenization of Complex Lattices for Metamaterials: Open Problems and Conjectures

Abstract

Based on concrete examples dealing with one-level periodic and quasi-periodic, and two-level periodic lattices, we show that the homogenization of complex lattices generically requires a multi-field continuum approach. We do not present results for specific cases, rather we discuss some related open problems and formulate pertinent conjectures. In this way, we suggest in essence a possible research program addressed towards the design of metamaterials.

1. Introduction

Although the need of sustainability for choices in engineering practice (more generally, in the way we exploit the resources of our planet) is a fairly recent growing awareness, with the consequent necessity of care when we choose materials in design practice, attempts to combine even recycled matter for specific services date back even before the practice of “opus incertum” made by the Romans.

It is therefore difficult to briefly outline an history of attempts to exploit natural materials with unusual properties or to create increasingly efficient composites up to the design of what we call metamaterials, a name coined in 1999 by R. M. Walser: artificial bodies engineered to have properties not available in naturally occurring materials and constituted by an assembly of microstructures.

We record metamaterials with a negative Poisson ratio, negative effective bulk modulus or even those with finite bulk but vanishing shear modulus so that they behave like fluids, despite being solid (foreseen in 1995 [1], fabricated in 2012 [2]). Current applications are in such areas as acoustics and optics, but the range is extending fast, with the design of new metamaterials for specific services.

In the design of large-scale structures, continuum models are expedient; for them, we need to bring at macroscopic scale information on the microstructure, exactly what we need to do for natural materials when a microstructure influences the gross behavior in a way that is hardly representable within the standard format of continuum mechanics as it is for liquid crystals, polarized matter, quasicrystals, polymeric suspensions and their like. The standard format of continuum mechanics, however, seems to be sufficient for metamaterials made of the periodic repetition of a homogeneously deforming single simple cell. Nevertheless, even for periodic assemblies, when the characteristic cell itself is made of interacting substructures, we need to describe their relative behavior. So, we introduce at continuum scale variables that complement a position of the cell mass center as we do in building up continuum models for the natural materials with the “active” microstructure mentioned above: vectors for polarization in ferroelectrics, second-rank tensors for polymers, etc.

The tendency of enriching the geometric description of continuous bodies, with respect to the classical format initiated by L. Euler, the Bernoullis, and, above all, A. L. Cauchy, dates back to the 1909 work by the brothers E. and F. Cosserat, who proposed to consider each material element as a small rigid body able to rotate freely with respect to its neighbors. Their proposal emerged long before the extended work by C. A. Truesdell’s school, which axiomatized, clarified, and extended from a foundational viewpoint the classical framework of continuum mechanics, especially through W. Noll’s work. In 1958, J. L. Ericksen and C. A. Truesdell adopted Cosserat’s ideas for modeling beams, plates, and shells [3]; then, between 1960 and 1962, Ericksen used elements of the projective plane to open the description of liquid crystals in the nematic phase; an idea further exploited, above all, by P. G. De Gennes, who adopted a second-rank tensor and eventually received the Nobel Prize in 1991 for his work in condensed matter physics [4]. In 1964, R. D. Mindlin considered material elements as cells able to deform independently [5], each micro-deformation described by a second-rank symmetric tensor. Materials represented by this choice or by stretchable directors are called micromorphic [6].

The subsequent literature concerning prominent special cases is abundant (see, for example, recent results in references [7,8,9,10,11,12,13,14,15,16,17,18]). An open question is, however, whether we can have a unified view on material complexity. In the late 1970s, G. Capriz started a pertinent unification program [19] by considering microstructural descriptors just as elements of an abstract manifold and coupling them with strain. The resulting theory includes as special cases the models of Cahn–Hilliard and Ginzburg–Landau, but also all the current phase-field models [20,21].

General order parameters were already used in 1937 by L. D. Landau in his theory of second-order phase transitions [22] and later in describing ordered media [23], but without considering the coupling with the macroscopic strain.

Among others, Capriz developed the approach above all with P. Podio-Guidugli (Lagrangian structures), E. G. Virga (algebra of bodies), P. Giovine (inertia and sparse media), and P. M. Mariano (Hamiltonian structures, junctions, and sparse media). Then, the last author developed procedures for the derivation of pertinent balance equations from invariance principles, showing how, in general, microstructures influence the evolution of defects [20,24]. In the static elastic case under a large strain regime, the existence of weak solutions in the unified framework was proven in 2009 by P. M. Mariano and G. Modica [25] (see also [26] for the micromorphic case; for spin structures and nematic liquid crystals described by elements of the projective plane see also, respectively, [27,28,29]); multiple-valued descriptors were also considered [30,31].

Here below, we show how such a framework is a natural theoretical ambient for describing at continuum scale metamaterials obtained by clustering complex microstructures. I do not offer specific results here, rather I discuss some open problems and formulate pertinent conjectures. The character of this paper is, in fact, exploratory. I believe that pondering the problems indicated here might provide an opportunity to make steps forward in the discrete-to-continuum modeling of materials and in the design of metamaterials.

2. One-Level Periodic Lattices

Consider in 3D real space three linearly independent vectors, say ${\mathbf{e}}_1,{\mathbf{e}}_2$, and ${\mathbf{e}}_3$, attached at a point O. They are the generators of a single periodic point lattice consisting of all points determined by linear combinations of the type $k_1{\mathbf{e}}_1+k_2{\mathbf{e}}_2+k_3{\mathbf{e}}_3$, with $k_i$ running in the set of natural numbers (a Bravais lattice, indeed). Translations by cell units along the generating vectors leave invariant the lattice itself. At each point determined by the above linear combination, the parallelepiped spanned by ${\mathbf{e}}_1$, ${\mathbf{e}}_2$, and ${\mathbf{e}}_3$ attached at that point is called an elementary cell, or better, a simple elementary cell; all these cells, each of volume V, form a tessellation of the whole space if we consider the lattice to be infinite.

Assume that the lattice points are endowed with mass and each is connected with its first neighbors by springs. Additionally, indicate by ${\mathbf{t}}_{ij}$ the force exerted by a spring between the i-th mass point and its j-th first neighbor. If we presume to deform the lattice and to describe its behavior at continuum scale, i.e., forgetting its discrete structure, the first step is to define a deformation map $\varphi$ over the whole space occupied by the lattice; it is one-to-one, differentiable, and orientation preserving, in accord to standard choices. Let $F:=\nabla \varphi (x,t)$ be the deformation gradient at a point x and instant t, and ${\mathbf{r}}_{ij}={\mathbf{r}}_i-{\mathbf{r}}_j$ a vector connecting the i-th mass point with the j-th one, each placed at positions ${\mathbf{r}}_i$ and ${\mathbf{r}}_j$ evaluated from the origin O.

We assume that each primitive cell is very small with respect to the region occupied by the lattice, leaving smallness not precisely defined at this stage but such that the imposed deformation can be considered homogeneous when restricted to the primitive cell, so that the relative displacement ${\mathbf{u}}_{ij}$ between each $i-j$ pair changes as $F{\mathbf{r}}_{ij}$, where now F is evaluated in the cell mass center. Eventually, presume that the work performed in the primitive cell equalizes the density of the inner work in the continuum scheme, namely

$$V^{-1}\sum _{i,j}{\mathbf{t}}_{ij}·{\mathbf{u}}_{ij}=P·F$$

where the interposed dot indicates scalar product, and P is the first Piola–Kirchhoff stress. By assumption, the identity holds for any choice of the deformation, provided that the identity

$${\mathbf{u}}_{ij}=F{\mathbf{r}}_{ij}$$

is satisfied. By exploiting such a kinematic constraint, due to the arbitrariness of F, we obtain

$$P=V^{-1}\sum _{i,j}{\mathbf{t}}_{ij}\otimes {\mathbf{r}}_{ij},$$

(1)

where ⊗ indicates, as usual, the tensor product.

We then obtain an expression for stress at a point x in terms of interactions in the discrete structure and its geometry; in this way, we attribute properties of the primitive cell to each point of the region occupied by the discrete structure that we describe at continuum scale. In other words, the primitive cell describes the generic material element and its interactions with the neighbors (see also [32] for further details to the discrete-to-continuum transitions).

3. One-Level Quasi-Periodic Lattices

Shift now to a simple mass point lattice fitting the space but being quasi-periodic instead of periodic. Imagine it as being made of the vertices of a Penrose tiling. In this case, we cannot define a single primitive cell, but we speak of a dominant cell, with ancillary structures, commonly called worms. In 3D space, an appropriate dominant cell is an icosahedron, while a pentagon in the plane. Worms emerge clearly because we cannot tessellate neither the plane with pentagons nor the three-dimensional space with icosahedra.

The lattice in the previous section is adequately represented by a periodic function, say, the mass distribution $\rho$ localized at the lattice “atoms”. In the present case, $\rho$ is quasi-periodic, i.e., it is such that there is a continuous function f of n variables equating $\rho$, namely $\rho \left(x\right)=f(a_1,\dots ,a_n)$, with f being a periodic function of its entries with periods ${\omega }_1,\cdots ,{\omega }_n$ that are all strictly positive, and their reciprocals are rationally linearly independent.

Consider $\rho (·)$ to be one such function in 3D space. If we expand it in the Fourier series—thus transiting from the lattice to a continuous representation—we find for the k-th term in the expansion a representation like ${\rho }_{k}exp\left(\iota {\mathsf{\Phi }}_k\right)$, where $\iota$ is the imaginary unit and ${\mathsf{\Phi }}_k={\mathsf{\Phi }}_0+\mathbf{k}·u+{\mathbf{k}}^{\prime }·\nu$, with ${\mathsf{\Phi }}_0$ an initial “phase”, while $\mathbf{k}$, ${\mathbf{k}}^{\prime }$, u, and $\nu$ are 3D vectors. Thus, in 3D space, the continuum representation of a quasi-periodic mass point lattice involves six degrees of freedom [33] for each point. Consequently, to describe its mechanics, we need an additional vector field complementing the standard displacement one [34,35] (see also, for example, references [36,37,38] for specific applications developed in the limit of the vanishing microstructural self-action).

We can visualize the circumstance by considering that a n-dimensional quasi-periodic lattice can be viewed as the projection of a periodic array of mass points in a space of dimension $2n$ onto an incommensurate subspace. Consider, for example, a square mass point lattice in a plane; take a straight line inclined by an irrational angle with respect to the orthogonal directions defining the squared structure. 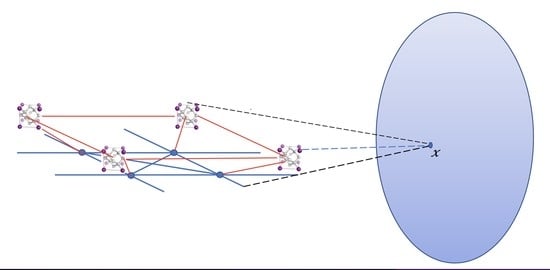Then, project along the direction orthogonal to the line all lattice mass points in a strip around the straight line: the result is a one-dimensional quasi-periodic lattice over the line (Figure 1 visualizes the scenario).

Then, a displacement in the plane decomposes into a component along the straight line, which is u in the Fourier expansion mentioned above such that $F=\nabla u+I$, with I being the second-rank identity tensor, and an orthogonal component to the line, which is $\nu$ in the same expansion. Such a circumstance does not necessarily imply that the continuum modeling of quasi-periodic structures should reduce to a standard one, provided it is formulated in an appropriate higher dimensional space, resulting in a replica of what is well known. In fact, the projection above is only a geometric construction. From a physical viewpoint, we have to look just at the one-dimensional quasi-periodic structure. Thus, in this view, $\nu$ represents (or has to be interpreted as an indicator of) inner degrees of freedom. Pertinent self-actions occur, defined by the power that they perform in the time rate of $\nu$ (provided we include time dependence to describe motions), besides additional contact ones, represented by a stress performing inner power in the time rate of the spatial derivative of $\nu$. Thus, the resulting representation falls within the general model-building framework for the mechanics of complex materials, as pointed out in references [35,39].

4. Two-Level Periodic Complex Lattices

Come back now to a periodic structure, but consider one such that each primitive cell is constituted by substructures, as it is for the two-level lattice in Figure 2 below.

Each sub-lattice $A_i$ has a different stiffness with respect to the ground one and also involves different masses. In describing a continuum scale of such a lattice, we need to describe the relative strain of each sub-lattice with respect to its first connected neighbors and the first-level lattice. Let us assume that the last one has a locally homogeneous deformation, as in the case of a simple one-level lattice, so that the rule ${\mathbf{u}}_{ij}=F{\mathbf{r}}_{ij}$ still holds in the discrete structure. Notice that we distinguish between the relative displacement $\mathbf{u}$ in the discrete structure and the displacement field u in the continuum scheme, where it is a field defined on the whole domain occupied by the tessellation associated with the lattice (so the reciprocal lattice).

Then, presume that each second-level sub-lattice admits also a homogeneous deformation, although with different strain. Let ${\mathsf{G}}_i$ be the gradient of such homogeneous deformation pertaining to the sub-lattice $A_i$, so that the relative displacement ${\mathbf{w}}_{hk}^i$ between the h-th and k-th interconnected mass points in $A_i$ is ${\mathbf{w}}_{hk}^i={\mathsf{G}}_i{\mathbf{s}}_{hk}$, where ${\mathbf{s}}_{hk}={\mathbf{s}}_h-{\mathbf{s}}_k$, with ${\mathbf{s}}_h$ and ${\mathbf{s}}_k$ being the position vectors of the h-th and k-th mass points, counted from the center of mass $x_i$ of the sub-lattice $A_i$. At continuum scale, we may presume that we have a second-rank tensor field, indicated by G, when evaluated at the mass center x of the complex cell above, such that ${\mathsf{G}}_i$ is given by the relation

$${\mathsf{G}}_i=G\left(x\right)+(\nabla G\left(x\right))(x_i-x).$$

Then, we have not only the actions defined by the work that they perform when F varies from the identity, but also those pertaining to G and those associated with DG. Thus, the internal work $P·F$ changes into

$$P·F+z·G+\mathcal{S}·\nabla G,$$

in which z is a bulk self-action in each sub-lattice and $\mathcal{S}$ is a stress, which we call a microstress because it is associated with the interactions between two neighboring substructures. By equating it with the power in the discrete structure, a combined use of the relations ${\mathbf{u}}_{ij}=F{\mathbf{r}}_{ij}$ and ${\mathsf{G}}_i=G\left(x\right)+(\nabla G\left(x\right))(x_i-x)$ allows us to determine all the interactions involved in terms of forces in the discrete net and the lattice geometry; namely, we obtain the expression of P given by Equation (2) and, with ${\mathbf{Ø}}_{hk}^i$ a force in the link between neighboring mass points h-th and k-th in the $A_i$ sub-lattice,

$$z=V^{-1}\sum _{h,k}{\mathbf{Ø}}_{hk}^i\otimes {\mathbf{s}}_{hk},$$

(2)

$$\mathcal{S}=V^{-1}\sum _{h,k}{\mathbf{Ø}}_{hk}^i\otimes {\mathbf{s}}_{hk}\otimes (x_i-x).$$

(3)

In the present case, the continuum representation is multi-field (displacement u and the sub-lattice descriptor G), and we have pertinent balance equations (see details in [19,20]). They are

(1)

The standard balance of forces

$$\mathrm{Div}P+b=\rho \ddot{u},$$

(4)

where b represents external body actions,

(2)

The balance of micro-actions

$$\mathrm{Div}\mathcal{S}+{\beta }^{‡}-z=0,$$

(5)

(3)

A local balance of couples

$$\mathrm{skw}P{F}^{*}=\frac{1}{2}\mathsf{e}\left({\mathcal{A}}^{\mathsf{T}}z+{\left(D{\mathcal{A}}^{\mathsf{T}}\right)}^t\mathcal{S}\right),$$

(6)

where the linear operator $\mathcal{A}$ is a third-rank tensor given by

$$\mathcal{A}=G\overline{\mathbf{e}}-\overline{\mathbf{e}}G,$$

(7)

with $\overline{\mathbf{e}}$ being the Ricci alternating index in ${\mathbb{R}}^3$ (see [20,24] from the derivation of such equations from invariance principles). The superscript $\mathsf{T}$ indicates standard transposition, while t means minor right transposition of third-rank tensors. ${\beta }^{‡}$ is the sum of inertial and non-inertial external direct actions on the microstructure; its inertial component depends on the relative inertia of the substructure with respect to the gross motion associated with the cell mass center.

5. Open Problems and Conjectures

In the scenario depicted so far, some open problems emerge among many for their role in opening potentially non-trivial research paths. We propose here a view on them, enforcing it with pertinent conjectures. The following discussion is the main novelty of the present paper.

5.1. About One-Level Periodic Lattices

• When referred to the discrete picture of periodic crystals, the constraint ${\mathbf{u}}_{ij}=F{\mathbf{r}}_{ij}$ is what we call the Cauchy–Born rule (see [40,41,42]). For two-dimensional mass–spring lattices, it constitutes a rigorous theorem for an open set of model parameters (equilibrium lengths and spring constants) for all boundary data close to the identity, while it fails for another open set of parameters [43]. Fine-scale spatial oscillations appear in that parameter region in the energy-minimizing configurations. However, viewing atoms as mass points is an idealization, possibly justified by the circumstance that, at zero temperature, a canonical ensemble (i.e., a system of interacting particles that is open to exchange energy with the environment but closed to mass transfer) becomes a degenerate distribution and localizes on (discrete) minimizers of the energy. Moreover, since elastically deformed states are in general just local minimizers of the energy, it is possible to prove that the Cauchy–Born rule is always valid for elastically deformed crystals, provided appropriate choices of the unit cell characterizing lattice periodicity [44,45]. However, the Cauchy–Born rule fails in some circumstances, for example, when inside a crystal, local slips occur [46].
• We can consider an affine-type approximation for the velocity distribution in an assembly of mass points that can or cannot be interconnected (in the first case, a lattice in a dynamic state or a cluster of identical linked molecules, and an avalanche of grains in the second case). In these circumstances, the introduction of an appropriate version of the Cauchy–Born rule makes sense after selecting a scale at which we decide to consider averages. By selecting a space window of that size, we can express the velocity of each mass point inside it at a given time as the mass center velocity of the window, an around-mass-center homogeneous motion, and a spurious fluctuation. The affine component is chosen to be optimal with respect to the kinetic energy [47,48]; in other words, it minimizes a difference between the mass–point kinetic energy and the sum of the mass center and affine motion kinetic energies. In this case, although the prototypical discrete structure is taken as a simple, statistically periodical (i.e., the distribution of masses is independent of the specific space window) discrete one, the resulting representation becomes always multi-field: the gross deformation describes the motion of the window center of mass, and a tensor field represents the around-mass-center motion of mass points into the window. Pertinent interactions emerge, as shown in the example of Figure 2, and they have to be appropriately balanced [47,49,50].

Problem 1.

To what extent can we adopt the local homogeneous deformation assumption in the elementary cell when the lattice behavior is elastic–plastic, or some shifts along the preferred directions occur and we aim at homogenizing the lattice in terms of power equivalence?

Conjecture 1.

In this case, we should work in (say) incremental terms, assuming that the point masses can have different velocities and considering the local homogeneity assumption in terms of time rates, a choice appropriate even when the cell is per se a deployable structure, so we need to put into correspondence powers rather than works. The approach implies, as in the above remark, that we have to identify how fluctuations, inducing local non-homogeneity in the velocity distribution, contribute to the overall behavior—and we think they essentially transfer collectively into an heating process—and how we can deduce flow rules at continuum scale in terms of the lattice properties.

Looking at the homogeneity assumption in terms of velocities (i.e., adopting a version of the Cauchy–Born rule in terms of velocities) establishes a bridge between the analysis of stable lattice and the discrete-to-continuum transition in representing the dynamics of sparse media. The starting point is then analogous; in the second case, however, the window in space is always a grand canonical ensemble from a statistical viewpoint (i.e., a system exchanging not only energy with the environment, but also mass). More precisely, we assign at each point x the statistical properties of a molecular cluster filling at the instant t a space window $\mathfrak{e}\left(x\right)$, a cube of side length $\delta$, through which grains, each with velocity w, may transit. With y, a vector issued from x that indicates places in $\mathfrak{e}\left(x\right)$, we presume to know a distribution $\mathsf{\Theta }(t,x;y,w)$ of velocities inside $\mathfrak{e}\left(x\right)$. Through $\mathsf{\Theta }$, we may define the overall averaged velocity

$$v\left(\tau ,x\right):={\delta }^{-3}{\int }_{\mathfrak{e}\left(x\right)}\left({\int }_{{\mathbb{R}}^3}\mathsf{\Theta }\left(\tau ,x;y,w\right)w(\tau ,x;y,w)\mathrm{d}w\right)\mathrm{d}y,$$

and a local averaged velocity $w_{*}$ at y inside $\mathfrak{e}\left(x\right)$, namely

$$w_{*}(t,x;y):={\left({\int }_{{\mathbb{R}}^3}\mathsf{\Theta }\left(t,x;y,w\right)\mathrm{d}w\right)}^{-1}{\int }_{{\mathbb{R}}^3}w\mathsf{\Theta }\left(t,x;y,w\right)\mathrm{d}w,$$

for which we accept the decomposition

$$w_{*}=v+By+c,$$

(8)

where the second-rank tensor B is presumed to be such that it best fits the kinetic energy, namely

$$B=\arg \underset{x\in \mathcal{B}}{min}{\int }_{\mathfrak{e}}\left({\int }_{{\mathbb{R}}^3}\mathsf{\Theta }\left(t,x;y,w\right)\mathrm{d}w\right)\left(\right|w_{*}{|}^2{-|v+By|}^2)\mathrm{d}y,$$

for every x and t. The tensor B is the time rate (when applied to y, it represents a velocity) of an affine component of the fluctuations with respect to the average velocity v. The associated affine deformation gradient G, itself a function of x and t, is a solution to the equation

$$\dot{G}=BG,$$

with initial datum that can be selected equal to the second-rank identity tensor; the superposed dot indicates total time derivative.

The resulting equations are such that the scheme is, in general, multi-field (compare [48] with [49,50] for different settings where these ideas apply). In the presence of internal constraints, the picture simplifies because the resulting balances collapse, reducing the equations (also depending on whether we consider fluctuations $c:=w_{*}-v-By$). The scheme involves second or higher-order neighbor interactions: the microstructural effects become latent in the sense that they just imply second-neighbor standard interactions represented by a hyperstress, i.e., a third-rank tensor field. In the special case in which the internal constraint is $F=G$ and some linear constitutive structures are introduced, the balance equations reduce to

$$\begin{array}{cc}\hfill v_t+(v·& \nabla )v+\nabla \pi +\mathrm{div}\left(H-\left(\nabla v_t+(v·\nabla )\nabla v\right)Y\right))\hfill \\ \hfill & =\mathrm{div}{\left(\overline{\mathbb{C}}\nabla u-2(\mathrm{div}(r_1\nabla \mathrm{sym}\nabla u+r_2\nabla \mathrm{sym}\nabla v)\right)}^{\top })+f,\hfill \end{array}$$

(9)

$$\mathrm{div}v=0,$$

(10)

$$H_t+(v·\nabla )H=J,$$

(11)

$$Y_t+(v·\nabla )Y=\nabla vY+Y\nabla v^{\top },$$

(12)

in which $u(x,\tau )$ and $v(x,\tau )$ are vectors (u is the integral of v over the interval $[0,\tau ]$), $H(x,\tau )$ and $Y(x,\tau )$ are second-rank symmetric tensors, f and J are the assigned vector and tensor, respectively, $\overline{\mathbb{C}}$ is a fourth-rank symmetric constant positive definite tensor, $\pi$ is a non-negative scalar, $r_1$, $r_2$, and $\nu$ are positive constants, and $\mathsf{\Lambda }={(-\mathsf{\Delta })}^{\frac{1}{2}}$, $\beta \ge 5/4$. Precisely, the binor Y and Reynolds’ tensor H are defined as follows:

$$Y(x,t):={\delta }^{-3}{\int }_{\mathfrak{e}\left(x\right)}\left({\int }_{\mathbb{V}}\mathsf{\Theta }\left(\tau ,x;y,w\right)\mathrm{d}w\right)y\otimes y\mathrm{d}y,$$

and

$$H(t,x):={\left({\int }_{\mathfrak{e}\left(x\right)}\left({\int }_{{\mathbb{R}}^3}\mathsf{\Theta }\left(t,x;y,w\right)\mathrm{d}w\right)\mathrm{d}y\right)}^{-1}{\int }_{{\mathbb{R}}^3}{\int }_{{\mathbb{R}}^3}\mathsf{\Theta }\left(t,x;y,w\right)\mathrm{d}wc\otimes c\mathrm{d}w.$$

Additionally, the index t indicates derivative with respect to time. Here, the displacement u is defined as the integral in time of v from 0 to $t>0$ at every point and time. The apex $\mathsf{T}$ indicates standard transposition.

These equations (see references [49,50] for an analysis of their origin) are naturally complemented by initial conditions

$$v(x,0)=v_0,u(x,0)=u_0,H(x,0)=H_0,$$

and various types of boundary conditions.

Problem 2.

Can such a scheme admit solutions, at least in a weak sense? In the affirmative case, what kind of regularity do they admit, depending on that of the initial data?

Answering these questions is essential before performing computations because we do not have (at least for sparse matter) benchmark closed-form solutions, and numerical convergence tests do not exhaust the problem of evaluating whether simulations tend to a “true” solution (albeit a weak one) of the problem in hands. The system is of a mixed type because it is hyperbolic in terms of velocity (with an elliptic constraint given by incompressibility) and parabolic in the Reynolds tensor describing fluctuations.

Conjecture 2.

We presume that a positive answer to the existence problem can be given when the system above is considered to be defined in the whole space ${\mathbb{R}}^2$. Additionally, in this case, the balance of forces (9) should be regularized by the introduction of a non-local-type inertia given, e.g., by $\nu {\mathsf{\Lambda }}^{2\beta }{v}_t$, where $\mathsf{\Lambda }={(-\mathsf{\Delta })}^{\frac{1}{2}}$, $\beta \ge 5/4$, and $\nu >0$ (a regularization of this type appears in analyses of the Euler–Voigt and Navier–Stokes–Voigt equations; see, for example, [51]). Then, the existence analysis would require preliminary energy-type estimates in terms of Galerkin’s approximation functions. Inequalities such as Gagliardo–Niremberg, Young, Poincaré, and Brezis–Wainger inequalities are expedient. We should also be helped by a relation of the type $Y={(\nabla u)}^{\mathsf{T}}\nabla u$ to be justified. Then, we would need a compactness criterion that could allow us to attain convergence of the Galerkin approximation. A consequent result would automatically establish the appropriate setting for the pertinent numerical simulations.

5.2. About One-Level Quasi-Periodic Lattices

Intrinsically quasi-periodic atomic arrangements (the adverb means that they are structures not obtained by simply modulating periodic atomic lattices) were recognized first in 1982 in rapid-cooled aluminum–manganese synthetic alloys. Experiments highlighted Bragg’s peaks in electron diffraction patterns distributed in a way that is incompatible with lattice translations [52]. This result influenced the definition of crystal after it was clear that such quasi-periodicity was not due to complicated twin structures, as presumed by L. Pauling in a strong criticism of Shechtman’s results. Presently, we know the existence of natural quasi-periodic crystals, called quasicrystals, discovered in meteorites [53]. Long-range incompatible order with periodic tessellation of 3D ambient space characterizes their structure, for example, an icosahedral phase in 3D space or a pentagonal one in the plane. Describing their mechanics is a matter of a multi-field approach [34,35,39,54]. So far, the analysis has been essentially focused on the elastic and visco-elastic behavior. In elasticity, the existence of minimizers of the pertinent energy was proven in reference [25] under large strains. For a linear elastic phase in a small-strain regime with dissipation at the microstructural level, the existence of weak solutions to the linear dynamics with non-linear macroscopic-microstructural coupling and gyroscopic effects was proven in reference [55]. For a linear viscoelastic quasi-periodic body with microstructural dissipation that occupies a fit region $\mathcal{B}$ in the three-dimensional ambient space, the pertinent balance equations referred also to a time interval $[0,\overline{t}]$ are

$$\begin{array}{cc}\hfill & \rho u_{tt}-ϵ\mathsf{\Delta }{u}_t=b+\mu \mathsf{\Delta }u+\xi \nabla \mathrm{div}u+\kappa \mathsf{\Delta }\nu +\overline{\xi }\nabla \mathrm{div}\nu ,\hfill \\ \hfill & \mathrm{in}\mathcal{B}\times [0,T],\hfill \\ \hfill & \begin{array}{cc}\varsigma {\nu }_t-\delta \mathsf{\Delta }{\nu }_t+\ell \left(\mathrm{curl}{u}_t\right)\times {\nu }_t=\hfill & \zeta \mathsf{\Delta }\nu +\gamma \nabla \mathrm{div}\nu \hfill \\ \hfill & +\kappa \mathsf{\Delta }u+\xi \nabla \mathrm{div}u-{\kappa }_0\nu ,\hfill \end{array}\hfill \\ \hfill & \mathrm{in}\mathcal{B}\times [0,\overline{t}],\hfill \\ \hfill & u(t,x)=0,\nu (t,x)=0,\hfill \\ \hfill & \mathrm{on}\partial \mathcal{B}\times [0,\overline{t}],\hfill \\ \hfill & {u|}_{t=0}=u_0,u_t{{|}_{t=0}={\dot{u}}_0,\nu |}_{t=0}={\nu }_0,\mathrm{on}\mathcal{B},\hfill \end{array}$$

(13)

where $u_0$, ${\dot{u}}_0$, and ${\nu }_0$ are assigned. The factors in front of u and $\nu$ derivatives are constitutive constants, and b is a forcing term (a bulk force, indeed).

Problem 3.

Can we prove the existence of an attractor in the pertinent dynamics? Can we prove the decay of energy at least in the linearized case, in which we leave a part of the non-linear gyroscopic term $\left(\mathrm{curl}{u}_t\right)\times {\nu }_t$? In this case, however, which type of boundary conditions are appropriate?

Conjecture 3.

The non-linear coupling does not allow to naturally foresee uniqueness such that a global attractor, if any (and we conjecture that it could be found, due to the presence of viscous-type interactions), should be a weak one. We should also find energy decay for the same reasons (viscosity is a dissipative phenomenon); however, we should require that the normal components of u and ν vanish at the boundary where also we should have $\mathrm{curl}u\times n=0$ and $\mathrm{curl}\nu \times n=0$.

Additionally, although a wide set of experiments on the elastic–plastic behavior and a number of theoretical analyses on dislocations in quasicrystals and their unusual peculiarities are available (see, for example, [56,57,58,59,60,61]), a description of continuum-scale quasicrystal overall elastic–plastic behavior has been not yet presented.

Problem 4.

How can we formulate it? To go into details, can we accept a multiplicative decomposition for the gradient of the necessary additional vector field already mentioned, as we do for the deformation gradient in common approaches to plasticity? If we would accept it, how could we justify it, e.g., accepting that this additional field is a special bounded variation function, as the deformation is for elastic–plastic materials?

Conjecture 4.

Once we have decided about the last two questions—that is a matter of modeling, although an affirmative answer seems to be acceptable—we could formulate a large strain description of quasicrystal plasticity based on a requirement of covariance for the second law, on the basis of a conceptual structure formulated and developed in reference [62].

However, besides questions associated with the mechanics of quasicrystals, what brings them within the path described here is that we may construct metamaterials with a quasiperiodic structure. Their description at continuum scale reproduces one of the natural and synthetic quasicrystals. A problem we have in this case is that we cannot recognize a unique elementary cell. So, the identification procedure based on power equivalence, as sketched in previous sections, does not work in the same way. Even when we restrict the analysis to the linear elastic setting, some coefficients remain unknown. To this aim, we should perform experiments on samples of quasi-periodic lattices obtained by additive manufacturing. The main idea could be to use image sensing, taking into account the limits with which a sensor can determine a material property depending on size and spatial resolution of the sensor, and the correlation length of fluctuations.

Such a type of lattice exhibits robust microwave-absorbing capacity in thin thickness. If the quasi-periodic structure is, e.g., a Penrose tiling, we achieve $12.2$ GHz in effective absorption bandwidth (reflection loss$<-10$ dB), from $5.78$ GHz to $18.00$ GHz with 2 mm thickness, with clear advantages in absorbing waves, if compared with corresponding periodic absorbers [63]. We could describe these properties by using the tools developed for analyzing the electro-optical behavior of crystals [64]; specifically, we would fall once again in the general model-building framework for the mechanics of complex materials and we should select different microstructural descriptor fields: one pertaining to the continuum modeling of a quasi-periodic structure, as above described, the other pertaining to charges.

5.3. About Two-Level Periodic Complex Lattices

In the example shown in Figure 2, imagine that some constraint allows the (schematic) second-level lattice to deform primarily along the preferred directions (see, for example, [65]). In this case, for example, instead of the second-rank tensor ${\mathsf{G}}_i$ already mentioned, we could describe coarsely the second-level lattice $A_i$ by means of a vector, say ${\mathsf{c}}_i$, presuming at continuum scale a vector field c such that ${\mathsf{c}}_i=\overline{c}\left(x\right)+(\nabla \overline{c}\left(x\right))(x_i-x)$. Possible choices of descriptor fields are generically manifold. However, internal constraints in the discrete lattice reflect at the continuum scale. Imagine in addition that irregularities exist in the lattice and induce bounded singularities that propagate as acceleration waves at the continuum scale. A related question is: How can we describe such waves in internally constrained complex continua? Based on the common treatment of internal constraints in multi-field theories (see [19,66]), we should answer this question in a general setting, by following some classical techniques [67]. In this way, we would have a general theory able to cover entire classes of models transferring at continuum scale properties of discrete microstructures.

Another question strictly deals with the discrete-to-continuum transition: it concerns the case in which the second-level lattice (see once again Figure 2) is a deployable structure. How should we behave? Indeed, we could work once again in terms of velocities, by adopting an assumption of local homogeneity, as above shown for clusters of grains, with a few details, but the issue has to be developed more carefully especially when we intend to consider the possibility of disconnections and reformation of bonds in the second-level lattice; these circumstances could be considered, in turn, toy models for some phenomena in soft matter.

When we look at optical or conductive properties of metamaterials, a problem is the description at continuum scale of the microstructural effects on those properties. A paradigmatic case in which such a problem appears to be crucial is the electromechanical behavior of biological filaments, such as axons in the human vision. An approach to this issue rests on the possibility of describing the electromechanical interactions in the presence of microstructures with the invariance techniques proposed in references [20,24,62].

Of course, all questions raised in the previous sections apply to the general setting discussed here, with an increasing level of difficulty to be tackled.

6. Additional Remark

Questions and possible perspective paths toward answers here indicated are varied in nature but have a common unifying ground: the general model-building framework for the mechanics of complex materials. The problems and related conjectures discussed above structure a possible research program that can be interesting from theoretical and technological viewpoints, a path that could stimulate appropriate sensibilities.