Fabrication and Characterization of Lead-Free BNT-6BT Ultrasonic Transducers Designed by an Intelligent Optimization Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. BNT-6BT Ceramics
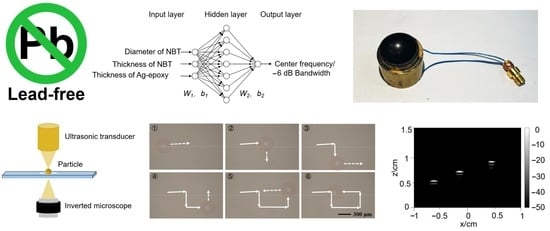
2.2. Optimization of Transducer Design
3. Results
3.1. Simulation and Experimental Results of Transducers
3.2. Imaging of Tungsten Rod Phantoms
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Uchino, K. Piezoelectric Actuators and Ultrasonic Motors; Springer: Boston, MA, USA, 1996. [Google Scholar]
- Mistewicz, K.; Jesionek, M.; Kim, H.J.; Hajra, S.; Kozioł, M.; Chrobok, Ł.; Wang, X. Nanogenerator for determination of acoustic power in ultrasonic reactors. Ultrason. Sonochem. 2021, 78, 105718. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Fei, C.; Lin, D.; Gao, P.; Zhang, J.; Quan, Y.; Chen, Z.; Yang, Y. A Review of Ultra High Frequency Ultrasonic Transducers. In New Piezoelectric Materials and Devices: Fabrication, Structures, and Applications; Frontiers Media: Lausanne, Switzerland, 2022. [Google Scholar]
- Jaffe, B.; Roth, R.S.; Marzullo, S. Piezoelectric properties of lead zirconate-lead titanate solid-solution ceramics. J. Appl. Phys. 1954, 25, 809–810. [Google Scholar] [CrossRef]
- Quan, Y.; Ren, W.; Niu, G.; Wang, L.Y.; Zhao, J.Y.; Zhang, N.; Liu, M.; Ye, Z.-G.; Liu, L.Q.; Tomoaki, K. Large Piezoelectric Strain with Superior Thermal Stability and Excellent Fatigue Resistance of Lead-free Potassium Sodium Niobate-Based Grain Orientation-Controlled Ceramics. ACS Appl. Mater. Interfaces 2018, 10, 10220–10226. [Google Scholar] [CrossRef] [PubMed]
- Jo, W.; Rödel, J. Electric-field-induced volume change and room temperature phase stability of (Bi1/2Na1/2)TiO3-x mol. % BaTiO3 piezoceramics. Appl. Phys. Lett. 2011, 99, 042901. [Google Scholar] [CrossRef] [Green Version]
- Ashura, N.I.; Topolov, V.Y. Lead-free 0–3-type composites: From piezoelectric sensitivity to modified figures of merit. J. Adv. Dielectr. 2013, 11, 2150010. [Google Scholar]
- Moya, B.R.; Silva, A.C.; Peláiz-Barranco, A.; Guerra, J.D.S. Structural, microstructural and dielectric characterizations of (Bi0.5Na0.5)TiO3 based lead-free ferroelectric ceramics. J. Adv. Dielectr. 2021, 11, 2140006. [Google Scholar] [CrossRef]
- Zhang, J.; Ren, W.; Liu, Y.; Wu, X.; Fei, C.; Quan, Y.; Zhou, Q. Fabrication and characterization of high-frequency ultrasound transducers based on lead-free BNT-BT tape-casting thick film. Sensors 2018, 18, 3166. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.Y.; Zhang, N.; Quan, Y.; Niu, G.; Ren, W.; Wang, Z.; Zheng, K.; Zhao, Y.; Ye, Z.-G. Evolution of mesoscopic domain structure and macroscopic properties in lead-free Bi0.5Na0.5TiO3-BaTiO3 ferroelectric ceramics. J. Appl. Phys. 2021, 129, 084103. [Google Scholar] [CrossRef]
- Huang, X.Y.; Gao, C.H.; Chen, Z.G.; Liu, H.P. Influence of Composition on Properties of BNT-BT Lead-Free Piezoceramics. J. Rare Earths 2006, 24, 321–324. [Google Scholar]
- Scopelliti, M.G.; Chamanzar, M. Ultrasonically sculpted virtual relay lens for in situ microimaging. Light Sci. Appl. 2019, 8, 565–579. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Xu, J.L.; Yang, L.L.; Liu, S.X.; Xiao, J.J.; Zhu, R.F.; Li, X.B.; Wang, X.; Luo, H.S. Fabrication of angle beam two-element ultrasonic transducers with PMN-PT single crystal and PMN-PT/epoxy 1-3 composite for NDE applications. Sens. Actuators A Phys. 2011, 168, 223–228. [Google Scholar] [CrossRef]
- Panda, S.; Hajra, S.; Mistewicz, K.; In-na, P.; Sahu, M.; Rajaitha, P.M.; Kim, H.J. Piezoelectric energy harvesting systems for biomedical applications. Nano Energy 2022, 100, 107514. [Google Scholar] [CrossRef]
- Fei, C.L.; Liu, X.L.; Zhu, B.P.; Li, D.; Yang, X.F.; Yang, Y.T.; Zhou, Q.F. AlN piezoelectric thin films for energy harvesting and acoustic devices. Nano Energy 2018, 51, 146–161. [Google Scholar] [CrossRef]
- Gudra, T.; Opieli’nski, K.J. Influence of acoustic impedance of mutilayer acoustic systems on the transfer function of ultrasionic airborne transducers. Ultrasonics 2002, 40, 457–463. [Google Scholar] [CrossRef]
- Fei, C.L.; Ma, J.G.; Chiu, C.T.; Williams, J.A.; Fong, W.N.; Chen, Z.Y.; Zhu, B.P.; Xiong, R.; Shi, J.; Hsiai, T.K.; et al. Design of matching layers for high-frequency ultrasonic transducers. Appl. Phys. Lett. 2015, 107, 123505. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.Y.; Fei, C.L.; Li, D.; Sun, X.H.; Hou, S.; Chen, J.; Yang, Y.T. Multi-layer polymer-metal structures for acoustic impedance matching in high-frequency broadband ultrasonic transducers design. Appl. Phys. 2020, 160, 107123. [Google Scholar] [CrossRef]
- Chen, D.; Wang, L.; Luo, X.; Fei, C.; Li, D.; Shan, G.; Yang, Y. Recent development and perspectives of optimization design methods for piezoelectric ultrasonic transducers. Micromachines 2021, 12, 779. [Google Scholar] [CrossRef]
- Wan, Z.; Chen, Y.; Huang, S.; Feng, D.D. A modified nonmonotone BFGS algorithm for solving smooth nonlinear equations. Optim. Lett. 2014, 8, 1845–1860. [Google Scholar] [CrossRef]
- Huang, S.; Wan, Z.; Deng, S.H. A modified projected conjugate gradient algorithm for unconstrained optimization problems. Anziam J. 2013, 54, 143–152. [Google Scholar]
- Krimholtz, R.; Leedom, D.A.; Matthaei, G.L. New equivalent circuits for elementary piezoelectric transducers. Electron. Lett. 1970, 6, 398–399. [Google Scholar] [CrossRef]
- Zhou, Q.F.; Lau, S.T.; Wu, D.W.; Shung, K.K. Piezoelectric films for high frequency ultrasonic transducers in biomedical applications. Prog. Mater. Sci. 2011, 56, 139–174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yan, X.; Ji, H.; Lam, K.H.; Chen, R.; Zheng, F.; Ren, W.; Zhou, Q.; Shung, K.K. Lead-free BNT composite film for high-frequency broadband ultrasonic transducer applications. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1533–1537. [Google Scholar] [PubMed]













| Design Parameters | Range |
|---|---|
| Diameter of BNT-6BT (mm) | 11, 12, 13, 14, 15, 16, 17, 18, 19 |
| Thickness of BNT-6BT (μm) | 745, 750, 755, 760, 765, 770, 775, 780, 785 |
| Thickness of Ag-epoxy (μm) | 155, 160, 165, 170, 175, 180, 185, 190, 195 |
| Parameter | tAg-epoxy | tBNT-6BT | Diameter | Bandwidth | Center Frequency |
|---|---|---|---|---|---|
| Mean value | 176.8 | 766.9 | 14.8 | 59.99 | 2.99 |
| Standard deviation | 0.0023 | 0.0023 | 0.0056 | 0.000044 | 0.0000035 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhao, J.; Quan, Y.; He, J.; Li, Y.; Wang, Z.; Zheng, K.; Zhuang, J.; Jiang, Z.; Wen, L.; et al. Fabrication and Characterization of Lead-Free BNT-6BT Ultrasonic Transducers Designed by an Intelligent Optimization Algorithm. Crystals 2022, 12, 1181. https://doi.org/10.3390/cryst12081181
Zhang J, Zhao J, Quan Y, He J, Li Y, Wang Z, Zheng K, Zhuang J, Jiang Z, Wen L, et al. Fabrication and Characterization of Lead-Free BNT-6BT Ultrasonic Transducers Designed by an Intelligent Optimization Algorithm. Crystals. 2022; 12(8):1181. https://doi.org/10.3390/cryst12081181
Chicago/Turabian StyleZhang, Junshan, Jianxin Zhao, Yi Quan, Jingrong He, Yi Li, Zhe Wang, Kun Zheng, Jian Zhuang, Zhishui Jiang, Li Wen, and et al. 2022. "Fabrication and Characterization of Lead-Free BNT-6BT Ultrasonic Transducers Designed by an Intelligent Optimization Algorithm" Crystals 12, no. 8: 1181. https://doi.org/10.3390/cryst12081181
APA StyleZhang, J., Zhao, J., Quan, Y., He, J., Li, Y., Wang, Z., Zheng, K., Zhuang, J., Jiang, Z., Wen, L., & Ren, W. (2022). Fabrication and Characterization of Lead-Free BNT-6BT Ultrasonic Transducers Designed by an Intelligent Optimization Algorithm. Crystals, 12(8), 1181. https://doi.org/10.3390/cryst12081181