Structural Study of Nematogenic Compound 5OS5
Abstract
:1. Introduction
2. Materials and Methods
- (a)
- first heating of a pristine sample which was not melted after synthesis,
- (b)
- heating after direct cooling with a 5 K/min rate from 365 to 263 K,
- (c)
- cooling from 365 to 298 K,
- (d)
- cooling from 365 to 298 K in the low-angle region only.
3. Results
3.1. DSC Thermograms
3.2. POM Observations
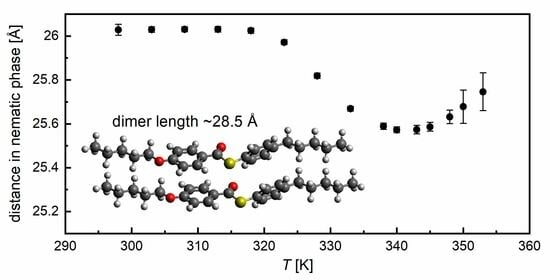
3.3. Structural Study by XRD
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Demus, D.; Goodby, J.; Gray, G.W.; Spiess, H.-W.; Vill, V. (Eds.) Handbook of Liquid Crystals; WILEY-VCH Verlag GmbH: Weinheim, Germany, 1998. [Google Scholar]
- Vertogen, G.; de Jeu, W.H. Thermotropic Liquid Crystals: Fundamentals; Springer: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Schadt, M. Nematic liquid crystals and twisted-nematic LCDs. Liq. Cryst. 2015, 42, 646–652. [Google Scholar] [CrossRef]
- Shivaraja, S.J.; Gupta, R.K.; Kumar, S.; Manjuladevi, V. Enhanced electro-optical response of nematic liquid crystal doped with functionalised silver nanoparticles in twisted nematic configuration. Liq. Cryst. 2020, 47, 1678–1690. [Google Scholar]
- Ma, Z.; Gao, Y.; Cao, H. The Effect of Chemically Modified Multi-Walled Carbon Nanotubes on the Electro-Optical Properties of a Twisted Nematic Liquid Crystal Display Mode. Crystals 2022, 12, 1482. [Google Scholar] [CrossRef]
- Stevenson, W.D.; Zhou, H.; Zeng, X.; Welch, C.; Ungar, G.; Mehl, G.H. Dynamic calorimetry and XRD studies of the nematic and twist-bend nematic phase transitions in a series of dimers with increasing spacer length. Phys. Chem. Chem. Phys. 2018, 20, 25268–25274. [Google Scholar] [CrossRef]
- Tomczyk, W.; Longa, L. Role of molecular bend angle and biaxiality in the stabilization of the twist-bend nematic phase. Soft Matter 2020, 16, 4350–4357. [Google Scholar] [CrossRef]
- Tschierske, C.; Photinos, D.J. Biaxial nematic phases. J. Mater. Chem. 2010, 20, 4263–4294. [Google Scholar] [CrossRef]
- Brisbin, D.; DeHoff, R.; Lockhart, T.E.; Johnson, D.L. Specific Heat near the Nematic-Smectic-A Tricritical Point. Phys. Rev. Lett. 1979, 43, 1171–1174. [Google Scholar] [CrossRef]
- Gane, P.A.C.; Leadbetter, A.J. Modulated crystal B phases and B-to-G phase transitions in two types of liquid crystalline compound. J. Phys. C Solid State Phys. 1983, 16, 2059–2067. [Google Scholar] [CrossRef]
- Leadbetter, A.J.; Tucker, P.A.; Gray, G.W.; Tajbakhsh, A.R. The Phase Behaviour of 4-n-Hexylphenyl 4-n-Tetra-Decyloxybenzthiolate (14S6) and 4-n-Pentylphenyl 4-n-Decyloxybenzthiolate (10S5). Mol. Cryst. Liq. Cryst. Lett. 1985, 1, 19–24. [Google Scholar] [CrossRef]
- Ocko, B.M.; Birgeneau, R.J.; Litster, J.D. Crossover to tricritical behavior at the nematic to smectic A transition: An x-ray scattering study. Z. Phys. B Condens. Matter 1986, 62, 487–497. [Google Scholar] [CrossRef]
- Chruściel, J.; Wróbel, S.; Kresse, H.; Urban, S.; Otowski, W. Dielectric Studies of 4-n-Pentylphenyl-4-Octyloxythiobenzoate. Mol. Cryst. Liq. Cryst. 1985, 127, 57–65. [Google Scholar] [CrossRef]
- Deptuch, A.; Jaworska-Gołąb, T.; Kusz, J.; Książek, M.; Nagao, K.; Matsumoto, T.; Yamano, A.; Ossowska-Chruściel, M.D.; Chruściel, J.; Marzec, M. Single crystal X-ray structure determination and temperature-dependent structural studies of the smectogenic compound 7OS5. Acta Cryst. B 2020, 76, 1128–1135. [Google Scholar] [CrossRef]
- Ossowska-Chruściel, M.D.; Karczmarzyk, Z.; Chruściel, J. The Polymorphism Of 4-N-Pentylphenyl-4″-N-Butyloxythio-Benzoate, (4OS5) In The Crystalline State. Mol. Cryst. Liq. Cryst. 2002, 382, 37–52. [Google Scholar] [CrossRef]
- Karczmarzyk, Z.; Ossowska-Chruściel, M.D.; Chruściel, J. The Crystal and Molecular Structure of 4-n-Pentylphenyl-4′-n-Hexyloxythiobenzoate (6OS5). Mol. Cryst. Liq. Cryst. 2001, 357, 117–125. [Google Scholar] [CrossRef]
- Chruściel, J.; Pniewska, B.; Ossowska-Chruściel, M.D. The Crystal and Molecular Structure of 4-Pentylphenyl-4′-Pentioxythiobenzoate (5S5). Mol. Cryst. Liq. Cryst. 1995, 258, 325–331. [Google Scholar] [CrossRef]
- Chruściel, J.; Wróbel, S.; Kresse, H.; Urban, S.; Otowski, W. Odd-Even Effect in the Homologous Series of Thioesters. Mol. Cryst. Liq. Cryst. 1990, 192, 107–112. [Google Scholar] [CrossRef]
- Rudzki, A. Liquid crystal mixtures with the chiral benzoate dopant. Phase Transit. 2023, 96, 139–148. [Google Scholar] [CrossRef]
- Osiecka, N.; Galewski, Z.; Massalska-Arodź, M. TOApy program for the thermooptical analysis of phase transitions. Thermochim. Acta 2017, 655, 106–111. [Google Scholar] [CrossRef]
- Osiecka-Drewniak, N.; Galewski, Z.; Juszyńska-Gałązka, E. Distinguishing the Focal-Conic Fan Texture of Smectic A from the Focal-Conic Fan Texture of Smectic B. Crystals 2023, 13, 1187. [Google Scholar] [CrossRef]
- Rodríguez-Carvajal, J. Recent advances in magnetic structure determination by neutron powder diffraction. Phys. B Condens. Matter 1993, 192, 55–69. [Google Scholar] [CrossRef]
- Cliffe, M.J.; Goodwin, A.L. PASCal: A principal axis strain calculator for thermal expansion and compressibility determination. J. Appl. Cryst. 2012, 45, 1321–1329. [Google Scholar] [CrossRef]
- Lertkiattrakul, M.; Ewans, M.L.; Cliffe, M.J. PASCal Python: A Principal Axis Strain Calculator. J. Open Source Softw. 2023, 8, 5556. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01, Gaussian, Inc.: Wallingford, CT, USA, 2019.
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- Blaabjerg, L.I.; Lindenberg, E.; Löbmann, K.; Grohganz, H.; Rades, T. Glass Forming Ability of Amorphous Drugs Investigated by Continuous Cooling and Isothermal Transformation. Mol. Pharm. 2016, 13, 3318–3325. [Google Scholar] [CrossRef]
- Jasiurkowska-Delaporte, M.; Rozwadowski, T.; Juszyńska-Gałązka, E. Kinetics of Non-Isothermal and Isothermal Crystallization in a Liquid Crystal with Highly Ordered Smectic Phase as Reflected by Differential Scanning Calorimetry, Polarized Optical Microscopy and Broadband Dielectric Spectroscopy. Crystals 2019, 9, 205. [Google Scholar] [CrossRef]
- Piwowarczyk, M.; Osiecka-Drewniak, N.; Gałązka, M.; Galewski, Z. Synthesis, mesogenic and photoisomerization studies of (E)-4-[(4-pentyloxyphenyl)diazenyl]phenyl alkanoates. Phase Transit. 2019, 92, 1066–1076. [Google Scholar] [CrossRef]
- Nakum, K.J.; Katarija, K.D.; Savani, C.J.; Jadeja, R.N. The influence of molecular flexibility on the mesogenic behavior of a new homologous series based on azo-azomethine: Synthesis, characterization, photoisomerization and DFT study. J. Mol. Struct. 2022, 1249, 131586. [Google Scholar] [CrossRef]
- Bagchi, K.; Emeršič, T.; Martínez-González, J.A.; de Pablo, J.J.; Nealey, P.F. Functional soft materials from blue phase liquid crystals. Science 2023, 9, eadh9393. [Google Scholar] [CrossRef] [PubMed]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Cryst. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Le Bail, A.; Duroy, H.; Fourquet, J.L. Ab-initio structure determination of LiSbWO6 by X-ray powder diffraction. Mater. Res. Bull. 1988, 23, 447–452. [Google Scholar] [CrossRef]
- Budai, J.; Pindak, R.; Davey, S.C.; Goodby, J.W. A structural investigation of the liquid crystal phases of 4-(2’-methylbutyl)phenyl 4’-n-octylbiphenyl-4-carboxylate. J. Phys. Lett. 1984, 45, 1053–1062. [Google Scholar] [CrossRef]
- de Vries, A. The description of the smectic A and C phases and the smectic A-C phase transition of TCOOB with a diffuse-cone model. J. Chem. Phys. 1979, 71, 25–31. [Google Scholar] [CrossRef]
- Rowland, R.S.; Taylor, R. Intermolecular Nonbonded Contact Distances in Organic Crystal Structures: Comparison with Distances Expected from van der Waals Radii. J. Phys. Chem. 1996, 100, 7384–7391. [Google Scholar] [CrossRef]
- Sinha, D.; Mandal, P.K.; Dąbrowski, R. High birefringence laterally fluorinated terphenyl isothiocyanates: Structural, optical and dynamical properties. Phys. B Condens. Matter 2014, 441, 100–106. [Google Scholar] [CrossRef]
- Bielejewska, N.; Chrzumnicka, E.; Mykowska, E.; Przybylski, R.; Szybowicz, M. Comparative Study of Orientational Order of Some Liquid Crystals from Various Homologous Series. Acta Phys. Pol. A 2006, 110, 777–793. [Google Scholar] [CrossRef]
- Bauman, D.; Zięba, A.; Mykowska, E. Oriental behaviour of some homologues of 4-n-pentyl-phenylthio-4′-n-alkoxybenzoate doped with dichroic dye. Opto-Electron. Rev. 2008, 16, 244–250. [Google Scholar] [CrossRef]









| Transition | (K) | (K) | (kJ/mol) | (J/(mol·K)) |
|---|---|---|---|---|
| Cr → N | 333.6 | 335.1 | 33.2 | 99.1 |
| N → X | 352.0 | 352.6 | 0.2 | 0.6 |
| X → Iso | 352.8 | 353.3 | 0.6 | 1.8 |
| Iso → X | 353.1 | 352.7 | −0.7 | −1.9 |
| X → N | - | 352.1 | −0.3 | −0.7 |
| N → Cr | 287.0 | 286.6 | −14.6 | - |
| Parameter | Pristine Sample | Crystal Grown from Melt | ||
|---|---|---|---|---|
| Intercept | Slope | Intercept | Slope | |
| a | 18.61(5) Å | 0.0042(2) Å/K | 18.99(3) Å | 0.00279(7) Å/K |
| b | 5.32(6) Å | 0.0010(2) Å/K | 5.476(4) Å | 0.00041(2) Å/K |
| c | 19.6(2) Å | 0.0026(5) Å/K | 19.39(2) Å | 0.00290(7) Å/K |
| β | 98.8(4)° | 0.021(2)°/K | 102.0(2)° | 0.0119(7)°/K |
| V | 1947(33) Å3 | 0.8(1) Å3/K | 1974(5) Å3 | 0.64(2) Å3/K |
| Principal Axis | a | b | c | [10−6/K] |
|---|---|---|---|---|
| x | 0.7298 | 0 | 0.6837 | −7.5(6.5) |
| y | 0 | −1 | 0 | 75(3) |
| z | −0.6880 | 0 | 0.7257 | 226(5) |
| V | - | - | - | 295(8) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deptuch, A.; Sęk, B.; Lalik, S.; Zając, W.; Ossowska-Chruściel, M.D.; Chruściel, J.; Marzec, M. Structural Study of Nematogenic Compound 5OS5. Crystals 2024, 14, 367. https://doi.org/10.3390/cryst14040367
Deptuch A, Sęk B, Lalik S, Zając W, Ossowska-Chruściel MD, Chruściel J, Marzec M. Structural Study of Nematogenic Compound 5OS5. Crystals. 2024; 14(4):367. https://doi.org/10.3390/cryst14040367
Chicago/Turabian StyleDeptuch, Aleksandra, Bartosz Sęk, Sebastian Lalik, Wojciech Zając, Mirosława D. Ossowska-Chruściel, Janusz Chruściel, and Monika Marzec. 2024. "Structural Study of Nematogenic Compound 5OS5" Crystals 14, no. 4: 367. https://doi.org/10.3390/cryst14040367
APA StyleDeptuch, A., Sęk, B., Lalik, S., Zając, W., Ossowska-Chruściel, M. D., Chruściel, J., & Marzec, M. (2024). Structural Study of Nematogenic Compound 5OS5. Crystals, 14(4), 367. https://doi.org/10.3390/cryst14040367