Strategies to Approach Stabilized Plasticity in Metals with Diminutive Volume: A Brief Review

Abstract

Micrometer- or submicrometer-sized metallic pillars are widely studied by investigators worldwide, not only to provide insights into fundamental phenomena, but also to explore potential applications in microelectromechanical system (MEMS) devices. While these materials with a diminutive volume exhibit unprecedented properties, e.g., strength values that approach the theoretical strength, their plastic flow is frequently intermittent as manifested by strain bursts, which is mainly attributed to dislocation activity at such length scales. Specifically, the increased ratio of free surface to volume promotes collective dislocation release resulting in dislocation starvation at the submicrometer scale or the formation of single-arm dislocation sources (truncated dislocations) at the micrometer scale. This article reviews and critically assesses recent progress in tailoring the microstructure of pillars, both extrinsically and intrinsically, to suppress plastic instabilities in micrometer or submicrometer-sized metallic pillars using an approach that involves confining the dislocations inside the pillars. Moreover, we identify strategies that can be implemented to fabricate submicrometer-sized metallic pillars that simultaneously exhibit stabilized plasticity and ultrahigh strength.

1. Introduction

The strength of metals increases when their size decreases to the micrometer scale. A review of the literature published during the last decade reveals numerous experimental and theoretical studies of materials with sample dimensions down to micrometers and/or nanometers, frequently described as a new regime to mediate the mechanical behavior of metals [1,2,3,4,5]. These studies turned out an important tenet, “smaller is stronger”, for material, which is consistent with the tendency of the tensile strength of whiskers reported by Brenner [6] 60 years ago. More recently, the impetus for this work has been provided by the ever-increasing demand for miniaturizing functional devices. Moreover, the parallel development of specimen preparation and mechanical testing techniques to study the behavior at the micrometer and nanometer scales has made these investigations feasible [7,8]. As reported by Uchic et al. [1], superior strength values, typically 3–8 times higher than the bulk strength, can be achieved in single crystal Ni and Ni₃Al-Ta by reducing the dimensions to micrometric scales. Additional decreases of sample dimensions down to the submicrometer (0.5 μm in diameter) scale for single crystal Ni₃Al-Ta can result in compressive flow stress values as high as 2.0 GPa, which represents the order of magnitude of the theoretical strength value. Further studies revealed similar ultrahigh strength for various metallic crystals with submicrometer dimensions, such as Ni [2,9], Au [3,10], Cu [11], Al [12], Ti [13], Mg [14], Mo [15], Nb [16], W [17], Ta [18] and Bi [19].

This dramatic enhancement of strength stems from fundamentally different deformation mechanisms in materials with a diminutive volume. Unlike bulk samples, dislocations in metals with submicrometer dimensions can only travel very short distances, leading to very limited multiplicative events. The reason for this behavior is that dislocations are annihilated at free surfaces due to image forces, thereby leaving the crystal in a dislocation-starved state (also known as mechanical annealing [2], shown in Figure 1a), which requires higher stress to nucleate new dislocations [20,21]. For pillars with a micrometer diameter, the single-arm dislocation source may be the dominant strengthening mechanism [22,23]. When the sample size is of the same order as the spacing between dislocations, the double-ended dislocation sources interact with the free surfaces and result in truncated single-arms of dislocations as schematically shown in Figure 1b. Either of the two deformation mechanisms can lead to a phenomenon known as “intermittent plastic flow”, which will be discussed in more details later.

The results discussed above, as well as a large body of literature have provided the impetus to use feature size as a design parameter that can be adjusted to achieve drastically-enhanced strength for microelectromechanical system (MEMS) devices, for example [24]. Current findings, however, reveal that the attainment of ultrahigh strength in many crystalline metals is consistently accompanied with disappointingly unstable plasticity, manifested as: (1) strain bursts that lead to unstable plastic flow [1,2,12]; and (2) strain softening and/or low strain hardening rates [3]. From an engineering standpoint, the presence of strain bursts results in unstable plastic flow during deformation and, thus, reduces the reliability of a mechanical system; from a scientific standpoint, these strain fluctuations prevent a material from approaching the theoretical value of the metals. Moreover, in terms of work hardening, the reported low strain hardening and/or strain softening that is frequently associated with a crystalline material with a diminutive volume limits the loading that can be sustained during deformation. Therefore, in order to enhance the mechanical reliability of micrometer-sized mechanical devices, it is of vital importance to suppress large strain bursts in order to achieve stable plastic flow, as well as to obtain appreciable strain hardening in micrometer- or submicron-sized crystalline materials.

A review of the published literature, however, reveals that a vast majority of published studies have concentrated on issues related to novel deformation mechanisms and the strength of the materials; and that the challenges posed by unstable plastic behavior have remained relatively unexplored. In view of this, the goal of this study is two-fold: first, to review and discuss recently published results, which suggest that it is indeed possible to attain the desired combination of stable plastic deformation and high strength; second, to describe a series of strategies that can be implemented to design the microstructure in micrometer- and/or submicron-sized crystalline samples to attain near theoretical strength values and stable plastic deformation.

The following points should be noted in this review paper. First, we limit our discussion to the plasticity and strength of metallic materials, rather than ceramic materials, e.g., Si nanowires [24,25], which also are known to exhibit sample size-induced plasticity; second, a discussion of instabilities that may originate from the experimental arrangement are not included in the scope of the current paper; third, a large portion of the published stress-strain curves (or load-displacement curves) discussed in this work were originally reported in an effort to study deformation mechanisms and strength, rather than plastic instabilities, e.g., the frequency of strain burst and the magnitude of strain burst. Accordingly, in some cases, the data on strain bursts and work hardening presented in this review paper were extracted from the literature, which did not intentionally report the plastic instabilities of micropillars or nanopillars. Once the data were extracted, we conducted the associated quantitative (and qualitative) analysis in support of our discussion.

2. Onset of the Strain Bursts and Softening in Metals with Diminutive Volume during Deformation

The plastic deformation of metals with micrometer- or nanometer-scale dimensions generally involves discontinuous plastic flow. Figure 2 shows a typical stress-strain curve of a single crystal <001>-oriented Au pillar compressed at a constant strain rate [3]. After linear compression and slight yielding, the first burst of the plastic flow occurred when the strain was about 3% (as indicated by the first hollow arrow). Further compression of the pillar resulted in multiple bursts of the plastic flow on the stress-strain curve. Larger bursts indicated by the 4th, 6th and 7th hollow arrows occurred in a random manner. These intermittent plastic flow events are described in the literature as strain bursts. Notably, this strain burst phenomenon is independent of deformation mode, e.g., compression or tensile with a constant load, for metals with micro- or nano-scale dimensions.

Csikor et al. [26] utilized three-dimensional discrete dislocation dynamics (3D-DDD) simulations and demonstrated that strain bursts in microcrystals arise from the collective, avalanche-like motion of dislocations. The constraints to the motion imposed by the crystal lattice structure provide dislocations with the ability to mutually trap each other into jammed configurations. The long-range mutual interactions between dislocations render the destruction of the jammed configurations a collective, avalanche-like process resulting in multiple strain bursts. This physical model was validated by in situ TEM studies performed by Wang et al. [12]. In this work, an Al pillar of 165 nm in diameter is characterized by very high collapse stresses and a nearly dislocation-free microstructure after the strain burst. However, for the pillars 440 nm in diameter, the jammed dislocations annihilated gradually from the free surface leading to strain bursts with a lower stress level. This observation is consistent with the dislocation starvation mechanism (also known as mechanical annealing). It reveals that the dislocation annihilation from free surfaces is size dependent and manifested by strain bursts with different stress levels. For metals with micrometer dimensions, the dislocation starvation mechanism might be no longer valid, and single-arm dislocation sources would be active in these scenarios. The 3D-DDD simulations [23] indicated that the dislocation density jumped drastically during the deformation in micrometer pillars; the single-arm dislocation sources can eventually leave the crystal, leading to a nearly defect-starved state. This suggests that the single-arm dislocation sources could be an operative mechanism for strain bursts. In situ tensile tests carried out by Oh et al. [27] indicated that single-end dislocation sources bulged out and were released from the surface. It is noted that the dislocations stop near the surface before they escape. The first dislocation stops for a longer time than the successive dislocations, which would result in intermittent slip bursts.

The above deformation mechanisms enable the feasibility of the strain bursts via the fast escape of the dislocations. However, the occurrence and the magnitude of the strain bursts are unpredictable. Maaß et al. [28] investigated the Au pillars with diameters of 300 nm, 500 nm, 2 μm and 5 μm with a data acquisition rate of 7 kHz to reveal the high resolution displacement during compression. For both micrometer and submicrometer pillars, the collective motion of dislocations was dominated by the statistical fluctuation within the internal stress, and the stress independence was unexpected. Up to date, however, there is a conspicuous absence of the experimental validation of the theory of dislocation annihilation and collective displacement of the metals at the atomic level. Revealing such dislocation dynamics related to the strain bursts will require in situ high resolution TEM studies recorded with a very high frequency rate (e.g., frames per second).

In bulk crystalline materials, it is well documented that strain hardening is attributable to the formation of dislocation tangles and their storage as a result of interactions with grain boundaries and/or dispersed particles [29]. Unlike bulk specimens, however, the multiplication of dislocations in micrometer- or submicrometer-sized pillars is difficult as dislocations travel a very short distance and ultimately escape from the free surfaces. Thus, micropillars or nanopillars tend to show strain softening or limited strain hardening [1,3,30,31,32].

3. Early Extrinsic Strategies to Stabilize Plasticity and Limits

To achieve a stable plastic flow in micrometer-sized pillars, Ng and Ngan proposed and established the concept of “extrinsic” approaches in their elegant paper [33]. In this work, it was reported that strain bursts were eliminated by depositing a W coating onto Al columns with diameters around 6 μm, as illustrated in Figure 3a. Moreover, an appreciable degree of work hardening was also obtained using this approach. Interestingly, the rate of strain hardening was reportedly correlated to the volume fraction of the W coating, and it was suggested that the dislocations were trapped into the Al crystals by the W coatings as indicated by the postmortem TEM images (Figure 3b). Therefore, trapping dislocations inside the pillar can suppress the strain bursts in micropillars, in which the size effect initially resulted in mild dislocation storage without coating. Accordingly, the multiplication of dislocations inside the micropillars led to strain hardening. However, the stress-strain curves exhibit jerky and unstable characteristics when the dimension of the pillar was decreased to 1 μm.

In addition to the coating strategy, Ng et al. [33] also used a focused ion beam (FIB) to mill an annular cavity deep at the center of micrometer-sized Al pillars. This central annular cavity was subsequently filled with W, as seen in the SEM images in Figure 3c. Some pillars were milled with cavities, but without any W filling. The stress-strain curves show that the micropillars containing W in the cavity exhibited smooth plastic flow, whereas micropillars with no W revealed erratic curves that are characteristic of unstable plastic flow. This phenomenon was interpreted by the fact that the pillar without W filling exhibited a crater structure, of which the thin shell facilitates the dislocation annihilation easier than that of the W-filled crater. The underlying dislocation dynamics is still unclear in the coated micrometer Al pillars and pillars with the W-filled crater; and further investigations are needed. However, we could speculate that the coating and W-filled crater approaches effectively alter the dislocation storage by intensive dislocation multiplication. The magnitude of dislocation avalanche and that of strain bursts were significantly reduced, leading to continuous plastic flow during the compression of the micropillars.

Some disadvantages that are inherent to the extrinsic strategies described here are: the cost of a coating on a micrometer-sized pillar, as well as the geometrical limitations associated with a cavity. For those micrometer-sized building blocks with very complex geometries, a conformal coating in a dual beam SEM/FIB system is extremely difficult.

An increase in sample size imparts more volume and thereby enables the onset of dislocation storage that is required for stable plastic flow during deformation and work hardening. This strategy has been demonstrated to be valid, not only for single crystal materials, but also for specimens that contain multiple crystals [32]. A drawback of such a strategy, however, is that there is a decrease in strength that accompanies an increase in sample volume.

4. Suppressing Strain Burst by Intrinsic Defects

4.1. Effect of the Interaction between Dislocations and the Grain Boundary on Plasticity

An approach that can be implemented to achieve stable plastic flow in micrometer-sized pillars involves incorporating intrinsic defects, such as grain boundaries (GBs), into pillars; strategies are heretofore described as intrinsic. One of the earliest documented studies involving this strategy is attributed to Ng et al. [34], who worked on pillars with 6-µm diameters, containing a vertical GB intersecting the top surface shown in Figure 4a,b; these pillars were fabricated via FIB milling from GB regions in a coarse-grained polycrystalline Al matrix. When deformed under compression by a flat-ended nanoindenter tip, the mechanical response of these bi-crystal pillars exhibits smaller strain bursts as compared to those of the single crystal counterparts of a similar size, as depicted in Figure 4c. Moreover, the bi-crystal pillars exhibit an enhanced work hardening response. Postmortem TEM studies of these pillars showed that there was significant dislocation accumulation at grain interiors near the GB (Figure 4d). On the contrary, the residual dislocation density remained low in the case of single crystal pillars. These results suggest that GBs limit dislocation movement, thereby augmenting dislocation storage. Hence, the effective interactions of GBs and dislocation forests effectively facilitated strain hardening, and this effect was absent in single crystals of the same material. Moreover, these results suggest that conventional Taylor strengthening remains valid in pillars with diameters of approximately 6 µm. However, the interactions between dislocations and GBs failed to occur when the pillar size was reduced to dimensions smaller than 1 μm; this phenomenon is discussed in a subsequent section.

An advantage of this intrinsic approach is that the strain burst can be effectively suppressed via introducing a GB. As compared to extrinsic methods, this strategy is effective, controllable and more cost effective. It should be mentioned that the size of the pillars in Ng’s work remains in the range of micrometers [33,34]. Furthermore, the maximum strength of these bi-crystalline Al pillars is only about 120 MPa, which is significantly lower than that required in many ultrahigh strength applications.

Analogous to the micrometer-sized Al pillars containing a vertical GB intersecting the top surface in Ng’s work, Kunz et al. investigated Al pillars with diameters ranging from 400 nm–1000 nm [35]. However, these submicron bi-crystalline Al pillars exhibited intermittent strain bursts, as shown in Figure 5. Moreover, lower hardening angles of the compressive stress-strain curves for the bi-crystalline pillars are evident in this figure, implying little or no dislocation storage. It is argued that GB in micrometer pillars acts by dislocation blocking or as a barrier, while the GBs in submicrometer or nanometer pillars are the dislocation source or sink. This finding is contrary to that in the larger sized bi-crystalline Al pillars with a GB reported by Ng et al. The postmortem TEM analysis confirmed such a hypothesis, as the near boundary regions appear to be defect free, with no evidence of dislocation pile-ups. Therefore, the suppression of strain bursts via vertical GB is indeed constrained by the size effect, and accordingly, this strategy will not work for pillars with submicron dimensions.

4.2. Effect of Grain Boundary Sliding on the Plasticity

In contrast to the case of a vertical GB, the effect of a slanted GB on the plastic behavior of submicron-sized pillars was investigated. Reported by Aitken et al. [36], uniaxial compression was applied onto 900 nm-diameter Al bi-crystals, which contained a high-angle GB with a plane normal inclined at 24° to the loading direction. As shown in Figure 6c, the compressive stress-strain curve was continuous compared to the single crystalline nanopillars, which revealed a stochastic stress strain signature. The curve displayed a peak in stress at the elastic limit of ~176 MPa followed by gradual softening and a plateau around ~125 MPa. These results revealed that frictional sliding along the boundary plane was the dominant deformation mechanism [36]. The top crystallite sheared off as a single unit during compression testing instead of crystallographic slip and extensive dislocation activity. Their post-deformation SEM images conveyed that nearly all plastic deformation was carried by this GB sliding. An energetics-based physical model disclosed that although the sliding mechanism is energetically favored from the beginning, the initial speed of sliding is low. Additionally, the stress-strain data are approximately elastic for the first few time steps before reaching peak stress. The stress then quickly decreases to a minimum value before increasing to a plateau when the sliding rate matches the displacement rate.

The above two studies indicate that introducing a single GB into a nanopillar could result in an unusual mechanical response, depending on the geometry of the GB. The GB could either slide or be curved to accommodate plastic deformation. We propose that the curved GB is related to the dislocation-driven plasticity, which resulted in the occurrence of strain bursts. However, grain rotation and GB sliding related to the GB-mediated deformation, which in turn leads to continuous plastic flow, still result in strain softening. Inspired by the above studies, it then follows that the introduction of multiple GBs into a pillar may be an effective approach to achieve improved plasticity. To that effect, Gu et al. [37] studied Pt pillars containing nanograins with an average grain size d = 12 nm. Their results suggest that the number of grains across the pillar diameter affects the plasticity (and also strength). The plastic flow of the pillars during the deformation became unstable with decreasing pillar diameter. This size-dependent behavior is due to the competition between accommodation of the applied load by GB sliding at the surface grains and the nucleation and propagation of partial dislocations at interior grains.

In FCC metals, the orientation of slip systems also affects the plasticity of the pillar, especially for pillars with micrometer dimensions. Hirouchi et al. [38] studied the micrometer-sized bicrystalline Cu pillar with the sigma-3 coherent twin boundary along the pillar axis. It was found that pillars with maximum Schmid factors parallel to the GB plane exhibited large strain bursts. However, pillars with slip planes randomly oriented exhibit limited strain bursts with accompanying work hardening. The effect of Schmid factors should be considered for fabricating micrometer-sized pillars. Nevertheless, Schmid’s law will be invalid as the size of the pillar decreases [39].

According to the above discussion, it is concluded that the effectiveness of an approach involving the introduction of GB(s) to suppress the strain bursts depends on grain size and geometry. The grain size determines whether the GB(s) block the dislocations or alternatively become sinks or sources for dislocations. The strategy of utilizing the GB(s) as an intrinsic defect to tailor the plastic flow of the pillar needs to be carefully considered; the microstructure of the pillar needs to be thoroughly designed.

4.3. Incorporating Nanoscale Second Phase Particles and Multiple Grain Boundaries

On the basis of the above discussion, a feasible approach to achieve stable plastic flow during the deformation of micrometer or nanometer pillars is to effectively confine the dislocations within the materials. Thus, we hypothesized that strain bursts can be significantly suppressed by introducing nanoscale coherent precipitates, which can promote strong dislocation storage and multiplication. Moreover, this should also lead to enhanced strain hardening. To validate this hypothesis, we used the precipitation strengthened 7075 Al alloy, in which the majority of coherent GP zones and similarly-sized semi-coherent η’ phase precipitates were introduced as the second phase particles by means of a T6 heat treatment [40]. The 7075 Al alloy is an alloy with Zn, Mg and Cu as dilute solute atoms, which might cause the stress serrations during the macroscopically smooth plastic flow. This phenomenon is known as the Portevin-Le Chatelier (PLC) effect, which is rather well understood as the dynamic strain aging engendering a recurrent process of the pining and unpinning of dislocations from solute atoms [41]. In our 7075 Al alloy subjected to aging treatment, a large portion of the solute atoms formed the precipitates. Therefore, the effect of solute atoms on the pinning of dislocations would be trivial. Our previous work [42] showed that stress serrations on the engineering tensile stress-strain curves for the 7075 Al alloys with similar heat treatments can be negligible. The PLC effect can be ignored in 7075 Al alloys in this study. The strain bursts (discussed later) in submicrometer 7075 Al pillars were primarily due to the size effect.

In situ nano-compression tests were conducted to investigate the plastic flow behavior. The results show that in the case of the single crystal Al 7075 pillar containing a high density of G.P. zones, large strain bursts were present, albeit with a strong working hardening rate [41]. It was argued that although the presence of second phase particles led to significant dislocation pileups, dislocations escaped in a collective manner, resulting in larger strain bursts (Figure 7a3). The second type of pillar studied was characterized by the presence of a slanted single GB and a high density of second phase particles. The stress-strain curve (Figure 7b3) indicated that no strain bursts were observed during the initial loading part in the stress-strain curve (strain up to 0.22). This is because of the co-existence of second phase particles and a GB. As a consequence of being impeded by the second phase particles, the dislocations were confined in a small volume leading to a significant work hardening. Similar to the case represented by the bi-crystalline pillar [36], the presence of a GB inevitably facilitated GB sliding, thereby accommodating plastic deformation concurrently. Under these conditions, plastic deformation occurs in a smooth and continuous manner. As the strain increased, the sliding of this single GB became difficult as the GB was curved; and the GB sliding cannot compensate for the collective escape of dislocations. Therefore, notable posterior strain bursts were observed as the strain increased from 0.22–0.34.

We further hypothesized that multiple GBs coupled with a high density of second phase particles would lead to the suppression of strain bursts. To validate this hypothesis, the third type of submicron Al pillars with multiple crystals (individual grains) and second phase particles was prepared and tested via in situ nano-compression tests. The stress-strain curve in Figure 7c2 reveals continuous and smooth plastic flow during the entire compression cycle. The representative snapshots of the compression indicated the occurrence of GB migration, and the grain rotation of our postmortem TEM observations carried out on the deformed pillar disclosed that the original grains were refined and subjected to high lattice distortions; dislocations were tangled around the coherent second phase particles. The considerable difference in the order of the dislocation density supports the premise that a high density of dislocations was generated during deformation, and moreover, that these dislocations remained trapped in the pillar. Consequently, the stored dislocations tangled and piled up, resulting in the refinement of the original grains with random orientations, similar to the behavior in the bulk material [42]. However, as the strain exceeded a certain level, saturation in grain refinement leads to a steady-state grain size [43]. Further refinement is limited because of the enhanced mobility of GBs [44]. Once this grain size is attained, GB migration and rotation governed the plastic behavior. Therefore, the dislocation activities were limited, and the escape of the dislocations from the free surface was substantially suppressed. The entire deformation process is a dynamic balance between intragranular dislocation activities and GB activities. In the meantime, the stored dislocation generates a strong tendency to work harden.

In the above discussion, the approach involves confining dislocations in a pillar, to thereby activate a distinct deformation mechanism at a certain strain level to accommodate further plastic flow. There are, however, approaches that involve transformations, such as twinning. For example, a specific case in α-Ti alloy [13] showed that stress-strain curves are characterized with strain bursts when the pillar size is larger than 1 μm. Once the pillar size is below 1 μm, the plastic flow is smooth and continuous. The transition of the plastic flow from unstable to stable is because of the transition from mechanical twinning-induced plasticity in pillars with a larger size (micrometer in diameter) to dislocation-induced deformation in pillars with a smaller size (submicrometer in diameter).

5. Concluding Remarks and Future Directions

In this article, we have reviewed several methods to suppress plastic instabilities, specifically strain bursts, in metallic crystals with micrometer and/or submicrometer dimensions. Particularly, we addressed two points: (1) the physical theme to suppress the strain bursts is the confinement of dislocations in the material eliminating the dislocation avalanche; (2) the current strategies discussed and the associated benefits and drawbacks.

(1)

To attain stabilized plasticity, extrinsic routes were developed, including W coating deposition and a center-cavity with filled W material in a pillar. The W coating or filling on the pillar trapped the dislocations inside the pillar, which stopped the abrupt escape of the dislocations.

(2)

By introducing a single GB perpendicular to the top surface, strain bursts in micrometer-sized pillars were suppressed. It is suggested that this perpendicular GB piled up dislocations and resulted in dislocation accumulation inside the pillar. However, when the pillar size was decreased down to the submicron scale, this phenomenon failed to appear.

(3)

Alternatively, a single GB located in the pillar with an inclined angle normal to the axis could lead to a stable plastic flow, yet with strain softening. The continuous plastic flow is due to the fact that the deformation is driven by GB sliding rather than dislocation-mediated deformation. However, the shear stress to activate the GB sliding is higher than that during the sliding. Therefore, further sliding yields strain softening.

(4)

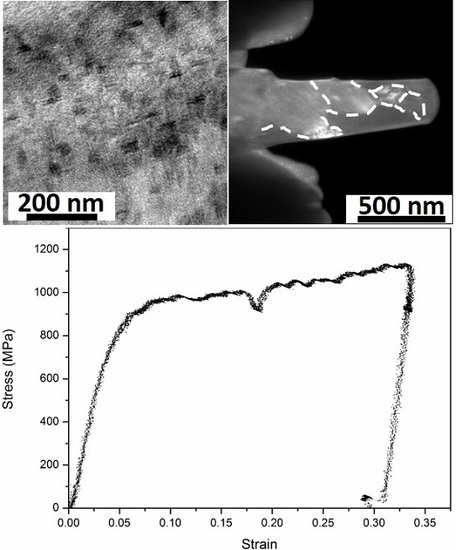
Submicron pillars containing multiple GBs and nanoscale coherent second phase particles exhibit continuous plastic flow, as well as considerable strain hardening. The highly dense second phase particles effectively pin the dislocations at the early stage of the deformation. This mechanism suppresses the strain bursts and also results in considerable strain hardening. Further deformation will trigger the GB-mediated deformation and give the dislocations no chance to escape from the pillar surface. A dynamic balance between dislocation storing and GB activities was achieved during the late stage of the compression, causing a stabilized plasticity and work hardening.

The work reviewed in this paper suggests that incorporating defects, such as multiple GBs and homogeneous second phase particles, represents an effective route to achieve stabilized plasticity in micrometer and/or submicrometer-sized pillars. Albeit that there are promising opportunities in this field, major challenges still remain, which dictate several future research directions, as follows:

• Further research should focus on the influence of other defects, such as twins, stacking faults and thermally-stable precipitates, on the plastic stability. By introducing these defects into the micrometer-sized and/or submicrometer-sized metals in an ordered or disordered manner, the plastic flow of the materials at such length scales will be influenced substantially. The revealing of the deformation mechanisms induced by each type of defect will provide insights to tailor the mechanical behavior.
• The atomic mechanism of strain bursts occurring in micrometer-sized and/or submicrometer-sized crystals needs more investigation. The jamming of dislocations and avalanche-like escaping phenomenon are still unclear. In situ high resolution TEM observation with high speed recording will be employed for experimental purpose. Molecular dynamics (MD) simulation is also required to reveal the atomic mechanism;
• While introducing the bulk defects, GBs also need to be tailored via element segregation. The GB activities, e.g., GB sliding, migration and rotation, will thus be modified in a controllable manner to achieve stabilized plasticity.