Liquid Crystal Ordering of Four-Base-Long DNA Oligomers with Both G–C and A–T Pairing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Synthesis and Purification
2.2. Sequence Characterization
2.3. Sample Preparation
2.4. Optical Microscopy
3. Results and Discussion
3.1. Pairing Modes of GCTA and Its Thermal Stability
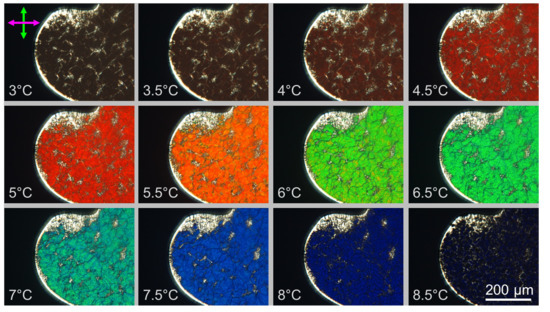
3.2. Phase Behavior of GCTA
3.3. Characterization of GCTA N* Phase
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Caruthers, H.M. Gene synthesis machines: DNA chemistry and its uses. Science 1985, 230, 281–285. [Google Scholar] [CrossRef] [PubMed]
- Rothemund, P.W.K. Folding DNA to create nanoscale shapes and patterns. Nature 2006, 440, 297–302. [Google Scholar] [CrossRef] [PubMed]
- Seeman, N.C. DNA in a material world. Nature 2003, 421, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, T.; Conwell, C.C.; Harvey, L.C.; Santai, C.T.; Hud, N.V. Condensation of oligonucleotides assembled into nicked and gapped duplexes: Potential structures for oligonucleotide delivery. Nucleic Acids Res. 2015, 33, 143–151. [Google Scholar] [CrossRef] [PubMed]
- Biffi, S.; Cerbino, R.; Bomboi, F.; Paraboschi, E.M.; Asselta, R.; Sciortino, F.; Bellini, T. Phase behavior and critical activated dynamics of limited-valence DNA nanostars. Proc. Natl. Acad. Sci. USA 2013, 110, 15633–15637. [Google Scholar] [CrossRef] [PubMed]
- Nakata, M.; Zanchetta, G.; Chapman, B.D.; Jones, C.D.; Cross, J.O.; Pindak, R.; Bellini, T.; Clark, N.A. End-to-end stacking and liquid crystal condensation of 6- to 20-base pair DNA duplexes. Science 2007, 318, 1276–1279. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Zanchetta, G.; Nakata, M.; Buscaglia, M.; Clark, N.A.; Bellini, T. Liquid crystal ordering of DNA and RNA oligomers with partially overlapping sequences. J. Phys. Condens. Matter 2008, 20, 494214. [Google Scholar] [CrossRef]
- Bellini, T.; Zanchetta, G.; Fraccia, T.P.; Cerbino, R.; Tsai, E.; Smith, G.P.; Moran, M.J.; Walba, D.M.; Clark, N.A. Liquid crystal self-assembly of random-sequence DNA oligomers. Proc. Natl. Acad. Sci. USA 2012, 109, 1110–1115. [Google Scholar] [CrossRef] [PubMed]
- Zanchetta, G.; Nakata, M.; Buscaglia, M.; Bellini, T.; Clark, N.A. Phase separation and liquid crystallization of complementary sequences in mixtures of nanoDNA oligomers. Proc. Natl. Acad. Sci. USA 2008, 105, 1111–1117. [Google Scholar] [CrossRef] [PubMed]
- Budin, I.; Szostak, J.W. Expanding roles for diverse physical phenomena during the origin of life. Annu. Rev. Biophys. 2010, 39, 245. [Google Scholar] [CrossRef] [PubMed]
- Fraccia, T.P.; Smith, G.P.; Zanchetta, G.; Paraboschi, E.; Yi, Y.; Walba, D.M.; Dieci, G.; Clark, N.A.; Bellini, T. Abiotic ligation of DNA oligomers templated by their liquid crystal ordering. Nat. Commun. 2015, 6, 6424. [Google Scholar] [CrossRef] [PubMed]
- Fraccia, T.P.; Zanchetta, G.; Rimoldi, V.; Clark, N.A.; Bellini, T. Evidence of Liquid Crystal–Assisted Abiotic Ligation of Nucleic Acids. Orig. Life Evol. Biosph. 2015, 45, 51–68. [Google Scholar] [CrossRef] [PubMed]
- Fraccia, T.P.; Smith, G.P.; Bethge, L.; Zanchetta, G.; Nava, G.; Klussmann, S.; Clark, N.A.; Bellini, T. Liquid crystal ordering and isotropic gelation in solutions of four-base-long DNA oligomers. ACS Nano 2016, 10, 8508–8516. [Google Scholar] [CrossRef] [PubMed]
- Taylor, M.P.; Herzfeld, J. Liquid-crystal phases of self-assembled molecular aggregates. J. Phys. Condens. Matter 1993, 5, 2651. [Google Scholar] [CrossRef]
- Van der Schoot, P.; Cates, M.E. Growth, static light scattering, and spontaneous ordering of rodlike micelles. Langmuir 1994, 10, 670–679. [Google Scholar] [CrossRef]
- SantaLucia, J.; Hicks, D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 415–440. [Google Scholar] [CrossRef] [PubMed]
- Peyret, N. Prediction of Nucleic Acid Hybridization: Parameters and Algorithms; Wayne State University: Detroit, MI, USA, 2000. [Google Scholar]
- De Michele, C.; Rovigatti, L.; Bellini, T.; Sciortino, F. Self-assembly of short DNA duplexes: From a coarse-grained model to experiments through a theoretical link. Soft Matter 2012, 8, 8388–8398. [Google Scholar] [CrossRef]
- De Michele, C.; Bellini, T.; Sciortino, F. Self-assembly of bifunctional patchy particles with anisotropic shape into polymers chains: Theory, simulations, and experiments. Macromolecules 2012, 45, 1090–1106. [Google Scholar] [CrossRef]
- Maffeo, C.; Luan, B.; Aksimentiev, A. End-to-end attraction of duplex DNA. Nucleic Acids Res. 2012, 40, 3812–3821. [Google Scholar] [CrossRef] [PubMed]
- Zanchetta, G.; Giavazzi, F.; Nakata, M.; Buscaglia, M.; Cerbino, R.; Clark, N.A.; Bellini, T. Right-handed double-helix ultrashort DNA yields chiral nematic phases with both right-and left-handed director twist. Proc. Natl. Acad. Sci. USA 2010, 107, 17497–17502. [Google Scholar] [CrossRef] [PubMed]
- Rossi, M.; Zanchetta, G.; Klussmann, S.; Clark, N.A.; Bellini, T. Propagation of chirality in mixtures of natural and enantiomeric DNA oligomers. Phys. Rev. Lett. 2013, 110, 107801. [Google Scholar] [CrossRef] [PubMed]
- Frezza, E.; Ferrarini, A.; Kolli, H.B.; Giacometti, A.; Cinacchi, G. The isotropic-to-nematic phase transition in hard helices: Theory and simulation. J. Chem. Phys. 2013, 138, 164906. [Google Scholar] [CrossRef] [PubMed]
- Livolant, F.; Maestre, M.F. Circular dichroism microscopy of compact forms of DNA and chromatin in vivo and in vitro: Cholesteric liquid-crystalline phases of DNA and single dinoflagellate nuclei. Biochemistry 1988, 27, 3056–3068. [Google Scholar] [CrossRef] [PubMed]
- De Michele, C.; Zanchetta, G.; Bellini, T.; Frezza, E.; Ferrarini, A. Hierarchical propagation of chirality through reversible polymerization: The cholesteric phase of DNA oligomers. ACS Macro Lett. 2016, 5, 208–212. [Google Scholar] [CrossRef]
- Lucchetti, L.; Fraccia, T.P.; Ciciulla, F.; Bellini, T. Non-linear optical measurement of the twist elastic constant in thermotropic and DNA lyotropic chiral nematics. Sci. Rep. 2017, 7, 4959. [Google Scholar] [CrossRef] [PubMed]
- Lucchetti, L.; Fraccia, T.P.; Ciciulla, F.; Simoni, F.; Bellini, T. Giant optical nonlinearity in DNA lyotropic liquid crystals. Opt. Express 2017, 25, 25951–25959. [Google Scholar] [CrossRef] [PubMed]
- Horowitz, E.D.; Engelhart, A.E.; Chen, M.C.; Quarles, K.A.; Smith, M.W.; Lynn, D.G.; Hud, N.V. Intercalation as a means to suppress cyclization and promote polymerization of base-pairing oligonucleotides in a prebiotic world. Proc. Natl. Acad. Sci. USA 2010, 107, 5288–5293. [Google Scholar] [CrossRef] [PubMed]





| ΔH (kcal mol−1) | ΔS (cal mol−1 K−1) | ΔG37 °C (kcal mol−1) | |
|---|---|---|---|
| ΔGGC | −27 | −72.2 | −4.61 |
| ΔGTA | −22.2 | −65.2 | −1.97 |
| ΔG* | −18.8 | −48 | −3.91 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fraccia, T.P.; Smith, G.P.; Clark, N.A.; Bellini, T. Liquid Crystal Ordering of Four-Base-Long DNA Oligomers with Both G–C and A–T Pairing. Crystals 2018, 8, 5. https://doi.org/10.3390/cryst8010005
Fraccia TP, Smith GP, Clark NA, Bellini T. Liquid Crystal Ordering of Four-Base-Long DNA Oligomers with Both G–C and A–T Pairing. Crystals. 2018; 8(1):5. https://doi.org/10.3390/cryst8010005
Chicago/Turabian StyleFraccia, Tommaso P., Gregory P. Smith, Noel A. Clark, and Tommaso Bellini. 2018. "Liquid Crystal Ordering of Four-Base-Long DNA Oligomers with Both G–C and A–T Pairing" Crystals 8, no. 1: 5. https://doi.org/10.3390/cryst8010005
APA StyleFraccia, T. P., Smith, G. P., Clark, N. A., & Bellini, T. (2018). Liquid Crystal Ordering of Four-Base-Long DNA Oligomers with Both G–C and A–T Pairing. Crystals, 8(1), 5. https://doi.org/10.3390/cryst8010005