Application of Evolutionary Rietveld Method Based XRD Phase Analysis and a Self-Configuring Genetic Algorithm to the Inspection of Electrolyte Composition in Aluminum Electrolysis Baths
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Method of Genetic Algorithm Self-Configuring
- Initially, the choice of any particular variant for each kind of operator (selection, crossover, mutation) is equiprobable. More specifically, the probability of choosing a variant of an operator is equal to p = 1/z, where z is the number of operator variants. It means that all variants of all operators are used equiprobably before statistics of their effectiveness are collected.
- On each generation, an effectiveness estimation is performed for each variant of each operator. It is based on the mean fitness of solutions obtained with the use of this variant of this operator: averagefitnessi = fi/ni, i = 1, 2, …, z, where averagefitnessi is the mean fitness of solutions obtained with the i-th variant of the operator; fi is the fitness sum of all solutions obtained with the i-th variant of the operator; ni is the number of solutions obtained with the i-th variant of the operator; i = 1, …, z, where z is the number of operator variants.
- For the next generation, the probability of using the most effective variant is increased by ((z − 1)·K)/(z·N) and probabilities of all other variants are decreased by K/(z·N), where N is the number of established generations of an algorithm run, K is a constant (usually equal to 2 for the considered problems). However, the probability of all variants cannot be lower than a given threshold, whereas the sum of all variant probabilities must be equal to 1. When an operator variant reaches this threshold, it will stop giving out part of its probability, and the best variant will no longer receive it. It is organized in this way because of the possibility that a variant could be unsuccessful on the first stages but could be very useful later on, and this could not happen if its probability decreased to zero.
- Operators used for the generation of a new solution are chosen stochastically according to obtained probability distributions.
2.2. Full-Profile QPA by Parallel Self-Configuring Genetic Algorithms
2.3. Objects of Investigations
- Tournament selection among 3, 5, 7, 9 trial models, range selection;
- Two-point crossover, three-point crossover, uniform crossover;
- Low-level mutation, average-level mutation, high-level mutation, with three standard deviations each.
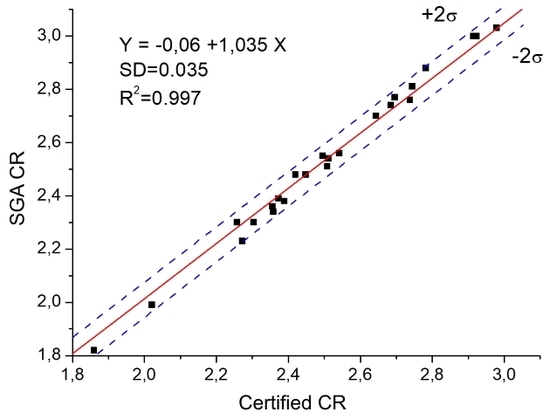
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Electrolytic Bath Standards; Alcan International Ltd.: Montreal, QC, Canada, 2005.
- Yakimov, I.S.; Dubinin, P.S.; Zaloga, A.N.; Piksina, O.E.; Kirik, S.D. Development of industry standard electrolyte samples of aluminum electrolyzers. Stand. Samples 2008, 4, 34–42. (In Russian) [Google Scholar]
- Feret, F.R. Breakthrough in analysis of electrolytic bath using Rietveld-XRD method. In Proceedings of the TMS2008: 137th Annual Meeting & Exhibition of the Minerals, Metals & Materials Society, New Orleans, LA, USA, 9–13 March 2008; pp. 343–346. [Google Scholar]
- Knorr, K.; Kelaar, C. Automated analysis of aluminium bath electrolytes by the Rietveld method. Miner. Eng. 2009, 22, 434–439. [Google Scholar] [CrossRef]
- Zaloga, A.; Akhmedova, A.; Yakimov, I.; Burakov, S.; Semenkin, E.; Dubinin, P.; Piksina, O.; Andryushchenko, E. Genetic Algorithm for Automated X-ray Diffraction Full-Profile Analysis of Electrolyte Composition on Aluminium Smelters. In Proceedings of the Informatics in Control, Automation and Robotics 12th International Conference, Colmar, Alsace, France, 21–23 July 2015; pp. 79–93. [Google Scholar] [CrossRef]
- Semenkin, E.; Semenkina, M. The Choice of Spacecrafts’ Control Systems Effective Variants with Self-Configuring Genetic Algorithm. In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics, ICINCO’2012, Rome, Italy, 28–31 July 2012; Ferrier, J.-L., Bernard, A., Gusikhin, O., Madani, K., Eds.; pp. 84–93. [Google Scholar]
- Semenkin, E.S.; Semenkina, M.E. Self-configuring Genetic Algorithm with Modified Uniform Crossover Operator. Adv. Swarm Intell. Lect. Notes Comput. Sci. 2012, 1, 414–421. [Google Scholar] [CrossRef]
- Bish, D.L.; Howard, S.A. Quantitative phase analysis using the Rietveld method. J. Appl. Cryst. 1988, 21, 86–91. [Google Scholar] [CrossRef] [Green Version]
- Favre-Nicolin, V.; Cerny, R. FOX, ‘free objects for crystallography’: A modular approach to ab initio structure determination from powder diffraction. J. Appl. Cryst. 2002, 35, 734–743. [Google Scholar] [CrossRef]
- Inorganic Crystal Structure Database. Available online: http://www2.fiz-karlsruhe.de/icsd_publications.html (accessed on 28 August 2018).



| # | Phase | Chemical Formula | Concentration Range, wt. % | CR Range |
|---|---|---|---|---|
| 1 | Cryolite | Na3AlF6 | 0–90 | >1.67 |
| 2 | Chiolite | Na5Al3F14 | 0–85 | <3.0 |
| 3 | Sodium fluoride | NaF | 0–5 | >3.0 |
| 4 | Ca-cryolite 1 | NaCaAlF6 | 0–15 | <3.0 |
| 5 | Ca-cryolite 2 | Na2Ca3Al2F14 | 0–20 | <2.95 |
| 6 | Fluorite | CaF2 | 0–9 | >2.45 |
| 7 | Weberite | Na2MgAlF7 | 0–15 | <2.85 |
| 8 | Neiborite | NaMgF3 | 0–6 | >2.5 |
| 9 | α-, β-, γ-alumina | Al2O3 | 2–5 |
| Phase | List of Refinable Parameters |
|---|---|
| Na3AlF6 | S, a, b, c, β, U, W, Eta0, Asym1, atomic coordinates (12 atomic positions), the texture hkl [220] by March-Dollase model |
| Na5Al3F14 | S, a, c, U, W, Eta0, Asym1, atomic coordinates (9 atomic positions) |
| NaCaAlF6 | S, a, b, c, β, U, W, Eta0, Asym1 |
| Na2Ca3Al2F14 | S, a, U, W, Eta0, Asym1 |
| CaF2 | S, a, U, W, Eta0, Asym1 |
| Na2MgAlF7 | S, a, b, c, U, W, Eta0, Asym1 |
| NaMgF3 | S, a, b, c, U, W, Eta0, Asym1 |
| α-Al2O3 | S, a, b, U, W, Eta0, Asym1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakimov, I.; Zaloga, A.; Dubinin, P.; Bezrukovа, O.; Samoilo, A.; Burakov, S.; Semenkin, E.; Semenkina, M.; Andruschenko, E. Application of Evolutionary Rietveld Method Based XRD Phase Analysis and a Self-Configuring Genetic Algorithm to the Inspection of Electrolyte Composition in Aluminum Electrolysis Baths. Crystals 2018, 8, 402. https://doi.org/10.3390/cryst8110402
Yakimov I, Zaloga A, Dubinin P, Bezrukovа O, Samoilo A, Burakov S, Semenkin E, Semenkina M, Andruschenko E. Application of Evolutionary Rietveld Method Based XRD Phase Analysis and a Self-Configuring Genetic Algorithm to the Inspection of Electrolyte Composition in Aluminum Electrolysis Baths. Crystals. 2018; 8(11):402. https://doi.org/10.3390/cryst8110402
Chicago/Turabian StyleYakimov, Igor, Aleksandr Zaloga, Petr Dubinin, Oksana Bezrukovа, Aleksandr Samoilo, Sergey Burakov, Eugene Semenkin, Maria Semenkina, and Eugene Andruschenko. 2018. "Application of Evolutionary Rietveld Method Based XRD Phase Analysis and a Self-Configuring Genetic Algorithm to the Inspection of Electrolyte Composition in Aluminum Electrolysis Baths" Crystals 8, no. 11: 402. https://doi.org/10.3390/cryst8110402
APA StyleYakimov, I., Zaloga, A., Dubinin, P., Bezrukovа, O., Samoilo, A., Burakov, S., Semenkin, E., Semenkina, M., & Andruschenko, E. (2018). Application of Evolutionary Rietveld Method Based XRD Phase Analysis and a Self-Configuring Genetic Algorithm to the Inspection of Electrolyte Composition in Aluminum Electrolysis Baths. Crystals, 8(11), 402. https://doi.org/10.3390/cryst8110402